海面GNSS-R 模型與時(shí)延-多普勒特征研究

萬林鈺，楊鵬舉，吳瑞，曹新亮，任新成

( 延安大學(xué)物理與電子信息學(xué)院, 陜西 延安 716000 )

0 引言

全球?qū)Ш叫l(wèi)星系統(tǒng)反射測(cè)量(Global Navigation Satellite System-Reflectometry，GNSS-R)是一種無源遙感技術(shù)，于1978 年被首次提出.該技術(shù)利用衛(wèi)星導(dǎo)航的反射信號(hào)進(jìn)行遙感，在風(fēng)速反演[1]、海面測(cè)高[2]和海面溢油探測(cè)[3]等海洋遙感領(lǐng)域具有重要的研究意義和廣闊的應(yīng)用前景.

自上世紀(jì)90 年代中期GPS 得到廣泛應(yīng)用以來，人們開始關(guān)注并深入研究GNSS-R 在海洋遙感領(lǐng)域的應(yīng)用.1988 年，Hall 等[4]首次提出了利用地球表面反射的GNSS 信號(hào)進(jìn)行散射測(cè)量的想法.1993 年，Martin-Neira[5]第一次提出了PARIS 的概念，以利用GNSS 反射信號(hào)進(jìn)行海洋測(cè)高.1998 年，Garrison等[6]首次在機(jī)載實(shí)驗(yàn)中證明可利用GPS 反射信號(hào)進(jìn)行風(fēng)速測(cè)量.2002 年，Lowe 等[7]首次在星載高度觀測(cè)到GNSS 反射信號(hào).2005 年，Gleason 等[8]在UK-DMC衛(wèi)星上檢測(cè)到GPS 海洋反射信號(hào)，表明利用近地軌道的雙基GNSS 反射信號(hào)進(jìn)行海洋遙感是可行的.

相較于國外，國內(nèi)在GNSS-R 技術(shù)領(lǐng)域的研究起步較晚，但取得了顯著進(jìn)展.2006 年，北京航空航天大學(xué)率先開展了利用GPS 信號(hào)進(jìn)行海面風(fēng)場(chǎng)探測(cè)的研究[9]，并成功研制出GNSS-R 接收機(jī)[10].近幾年，北京航空航天大學(xué)在GNSS 反射信號(hào)建模及遙感應(yīng)用方面進(jìn)行了大量的研究[11-13].

中國礦業(yè)大學(xué)構(gòu)建了星載GNSS-R 海浪有效波高的反演模型[14].武漢大學(xué)利用改進(jìn)的星載GNSS-R卷積神經(jīng)網(wǎng)絡(luò)進(jìn)行海冰探測(cè)研究[15].

近年來，各國相繼發(fā)射GNSS-R 接收衛(wèi)星，為GNSS-R 技術(shù)在海洋領(lǐng)域的應(yīng)用提供了大量實(shí)測(cè)數(shù)據(jù)資源.2014 年，英國薩里衛(wèi)星技術(shù)公司發(fā)射了TechDemoSat-1(TDS-1)衛(wèi)星，搭載GNSS-R 遙感儀器，以完成星載GNSS-R 測(cè)量的任務(wù)[16].NASA 于2016 年啟動(dòng)了旋風(fēng)全球衛(wèi)星導(dǎo)航系統(tǒng)(Cyclone Global Navigation Satellite System，CYGNSS)任務(wù)[17]，旨在監(jiān)測(cè)颶風(fēng)變化和熱帶氣旋.歐洲航天局和西班牙國家研究委員會(huì)也在這一領(lǐng)域積極展開研究.2019 年，中國自主研制的捕風(fēng)一號(hào)A/B 星發(fā)射成功，實(shí)現(xiàn)了利用衛(wèi)星導(dǎo)航信號(hào)進(jìn)行海面風(fēng)場(chǎng)探測(cè)的突破，對(duì)臺(tái)風(fēng)預(yù)警和防災(zāi)減災(zāi)具有重要意義[18].隨著我國自主研制的北斗衛(wèi)星導(dǎo)航系統(tǒng)(BeiDou Navigation Satellite System，BDS)[19]正式開通運(yùn)行，利用北斗衛(wèi)星反射信號(hào)進(jìn)行海洋遙感的應(yīng)用也越來越多[20-21].

對(duì)GNSS 反射信號(hào)建模與仿真分析是開展GNSS-R遙感應(yīng)用研究的重要基礎(chǔ).本文首先分析了GNSS 海面散射的幾何模型和GNSS 信號(hào)的結(jié)構(gòu)，然后建立了GNSS 反射信號(hào)模型，利用經(jīng)典Z-V 模型研究了海面反射信號(hào)的時(shí)延一維相關(guān)功率和時(shí)延-多普勒二維相關(guān)功率譜特征，討論了時(shí)延間隔和多普勒頻移間隔分別對(duì)時(shí)延一維相關(guān)功率和時(shí)延-多普勒?qǐng)D(delay-Doppler map，DDM)波形的影響.

1 GNSS-R 幾何模型與信號(hào)結(jié)構(gòu)

1.1 GNSS-R 幾何模型

GNSS 衛(wèi)星、海面與接收機(jī)的雙基雷達(dá)幾何模型如圖1 所示.對(duì)于本文中的海面散射問題，使用了固定在反射面上的局部散射坐標(biāo)系.原點(diǎn)設(shè)置在鏡面反射點(diǎn)處，z軸位于局部水平面的法線方向.y、o、z平面包括GNSS 衛(wèi)星、接收機(jī)和鏡面反射點(diǎn)，正y軸朝向GNSS 衛(wèi)星，x軸由右手正交法則可得.

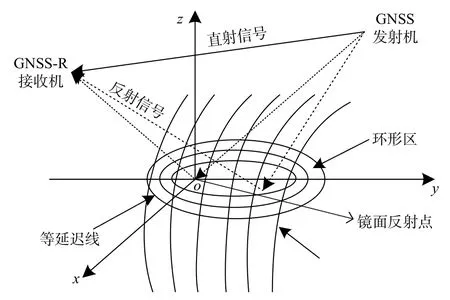
圖1 GNSS-R 幾何模型圖

GNSS 衛(wèi)星發(fā)射的信號(hào)經(jīng)由兩條路徑到達(dá)信號(hào)接收機(jī)，一是從GNSS 衛(wèi)星直接到接收機(jī)，信號(hào)中間傳播過程的衰減忽略不計(jì)；二是GNSS 衛(wèi)星到海面再到信號(hào)接收機(jī)，散射信號(hào)與直射信號(hào)相比，在時(shí)延和多普勒兩個(gè)維度上均有差異.GNSS 衛(wèi)星信號(hào)兩種到達(dá)接收機(jī)的方式，如圖1 所示.

1.2 GNSS 信號(hào)結(jié)構(gòu)

以BDS B1I 信號(hào)為例對(duì)GNSS 信號(hào)結(jié)構(gòu)進(jìn)行說明.BDS B1I 信號(hào)與其他GNSS 發(fā)射的信號(hào)如GPS L1 信號(hào)、Galileo E1 信號(hào)和GLONASS L1 信號(hào)具有相似的特點(diǎn)和相近的調(diào)制方式.B1I 信號(hào)在北斗二號(hào)(BeiDou-2Navigation Satellite System，BDS-2)和北斗三號(hào)(BeiDou-3Navigation Satellite System，BDS-3)系統(tǒng)的中圓地球軌道(medium earth orbit，MEO)衛(wèi)星、傾斜地球同步軌道(inclined geo-synchronous orbit，IGSO)衛(wèi)星和地球靜止軌道(geostationary earth orbit，GEO)衛(wèi)星上播發(fā)，提供公開服務(wù)[22].

BDS B1I 信號(hào)由“測(cè)距碼+導(dǎo)航電文”調(diào)制在頻率為1561.098MHz 的載波上構(gòu)成，其信號(hào)表達(dá)式為

式中：上角標(biāo)i為北斗衛(wèi)星編號(hào)；AB1I為信號(hào)振幅；CB1I為信號(hào)測(cè)距碼；DB1I為導(dǎo)航電文；f為B1I 信號(hào)的載波頻率；φB1I為信號(hào)初始相位.

BDS B1I 信號(hào)測(cè)距碼類似于GPS 信號(hào)中的擴(kuò)頻碼.測(cè)距碼稱為偽隨機(jī)噪聲(pseudo random noise code，PRN)序列，具有確定、周期性和良好的相關(guān)特性，BDS 優(yōu)先使用1~37 號(hào)測(cè)距碼.圖2 給出了BDS 4 號(hào)衛(wèi)星測(cè)距碼的自相關(guān)函數(shù).圖3 給出了BDS4 號(hào)和10 號(hào)衛(wèi)星測(cè)距碼的互相關(guān)函數(shù).圖2 和圖3說明了BDS B1I 信號(hào)測(cè)距碼具有良好的自相關(guān)和互相關(guān)特性，高自相關(guān)峰值和低互相關(guān)峰值可為信號(hào)捕獲提供很寬的動(dòng)態(tài)范圍.

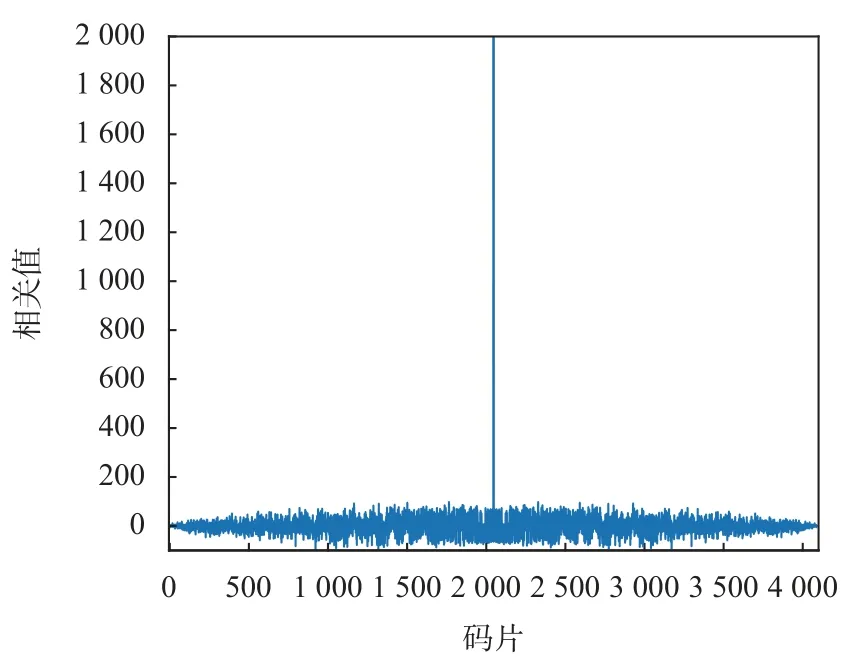
圖2 BDS 4 號(hào)衛(wèi)星B1I 信號(hào)測(cè)距碼的自相關(guān)函數(shù)

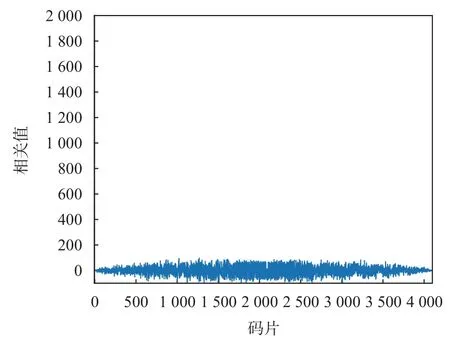
圖3 BDS 4 號(hào)和10 號(hào)衛(wèi)星B1I 信號(hào)測(cè)距碼的互相關(guān)函數(shù)

2 GNSS 反射信號(hào)模型

在實(shí)際測(cè)量中，GNSS-R 接收機(jī)平臺(tái)接收到的信號(hào)來自閃耀區(qū)內(nèi)多個(gè)散射點(diǎn)處反射信號(hào)的集合.由于反射信號(hào)的傳播路徑不同，不同散射點(diǎn)的時(shí)延也不同.GNSS-R 接收機(jī)、GNSS 衛(wèi)星和散射點(diǎn)始終處于相對(duì)運(yùn)動(dòng)狀態(tài)，因此不同散射點(diǎn)處的反射信號(hào)具有不同的多普勒頻率.故不同的時(shí)延間隔和多普勒頻率間隔對(duì)反射信號(hào)具有不同的影響，而海面的特征信息包含在不同的反射信號(hào)里.

2.1 伍德沃德模糊函數(shù)

雷達(dá)脈沖壓縮技術(shù)中，距離和多普勒頻率測(cè)量的不確定性是一個(gè)重要問題.為了分析這種不確定性，可以應(yīng)用模糊函數(shù)這一理論工具.該函數(shù)最初由伍德沃德引入用于雷達(dá)系統(tǒng)的分析.而在GNSS-R 中，雙基雷達(dá)方程是其理論基礎(chǔ)，因此也可借用伍德沃德模糊函數(shù)來進(jìn)行相關(guān)分析.故伍德沃德模糊函數(shù)χ(τ,f)可定義為[23]

式中： ?τ為時(shí)延變化值；?f為多普勒頻率變化值；Ti為積分時(shí)間；uPRN(·)為PRN 序列.

圖4 給出了矩形脈沖的模糊函數(shù)，它是實(shí)際PRN 模糊函數(shù)的理想化.由圖4 可知，該函數(shù)的最大值出現(xiàn)在原點(diǎn)(τ=f=0)處，值為1.

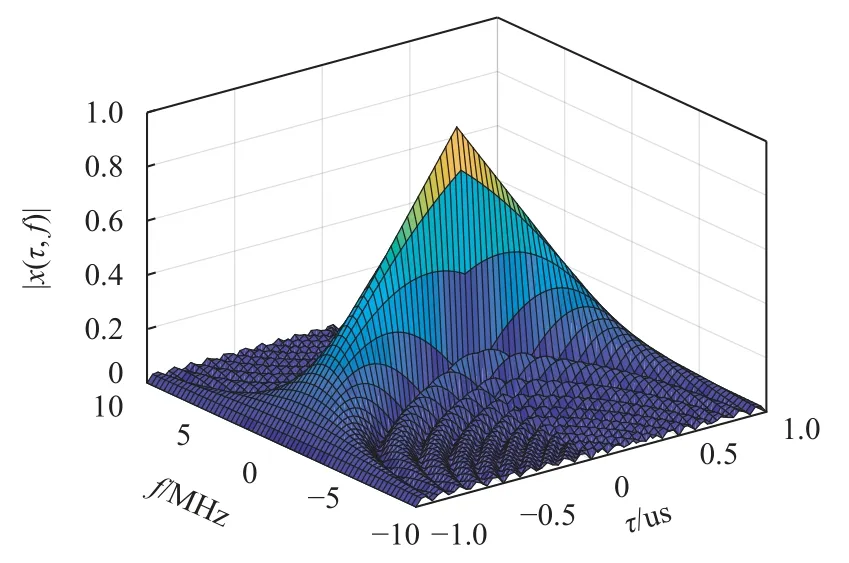
圖4 矩形脈沖的模糊函數(shù)

沿軸?τ=0(零延遲)和?f=0(零多普勒)的窄區(qū)域中，模糊函數(shù)可以用三角形相關(guān)函數(shù)Λ(?τ)及sinc型函數(shù)S(?f)的乘積來近似

Λ函數(shù)和S函數(shù)分別決定了等環(huán)形區(qū)和等多普勒區(qū).圖4 在零多普勒和零延遲時(shí)的切片分別為三角形Λ函數(shù)和具有相移的sinc函數(shù).

式中，τc為碼片周期.

2.2 時(shí)延一維相關(guān)功率

Zavorotny 和Voronovich 提出了一個(gè)經(jīng)典理論模型用于描述GNSS 散射信號(hào)的功率，該模型基于雙基雷達(dá)方程，使用基爾霍夫近似的幾何光學(xué)極限導(dǎo)出了散射信號(hào)的相關(guān)功率，表達(dá)式為[23]

其中，

式中： τ為兩條不同路徑的時(shí)間延遲，即從發(fā)射機(jī)-散射點(diǎn)-接收機(jī)和發(fā)射機(jī)-鏡面反射點(diǎn)-接收機(jī)的路徑；fd為多普勒頻移；Ti為相干積分時(shí)間；G是積分區(qū)域；D為接收機(jī)的天線增益；Λ為測(cè)距碼的自相關(guān)函數(shù)；S為多普勒濾波函數(shù)；Λ2(?τ)|S(?f)|2是上文提到的GNSS-R 雙基雷達(dá)模糊函數(shù)，描述了相關(guān)功率譜對(duì)時(shí)延和多普勒頻移的選擇性；r0和r分別為發(fā)射機(jī)、接收機(jī)到散射點(diǎn)的距離；ρ為平均海面上的某一散射點(diǎn)；σ0為歸一化散射截面(或散射系數(shù))，在KA-GO的近似條件下，可表示為

式中：R是菲涅爾反射系數(shù)；q是散射向量；P(·)是海面坡度概率密度函數(shù)(probability density function，PDF).文獻(xiàn)[24]利用Gram-Charlier 分布來描述海面坡度PDF，Gram-Charlier 分布通過修正二維高斯分布，在海面坡度PDF 中引入了偏度(skewness)和峰度(peakedness).GNSS 信號(hào)的等效均方坡度(mean square slopes,MSS)[25]：

其中，

式中，U表示海面風(fēng)速，單位為m/s.

反射信號(hào)的時(shí)延一維相關(guān)功率與海面的風(fēng)速和風(fēng)向等物理參數(shù)有著密切的關(guān)系[23].在接收機(jī)高度為682km，風(fēng)向與入射面夾角為0°的條件下，風(fēng)速為4~10m/s，間隔為2m/s 的反射信號(hào)時(shí)延一維相關(guān)功率曲線如圖5 所示.由圖5 可知，在不同風(fēng)速條件下，反射信號(hào)的時(shí)延一維相關(guān)功率曲線呈現(xiàn)出不同的特征.這種差異可以歸因于波形對(duì)海面風(fēng)速的敏感性，隨著風(fēng)速逐漸增大，波形后沿斜率也逐漸變大.

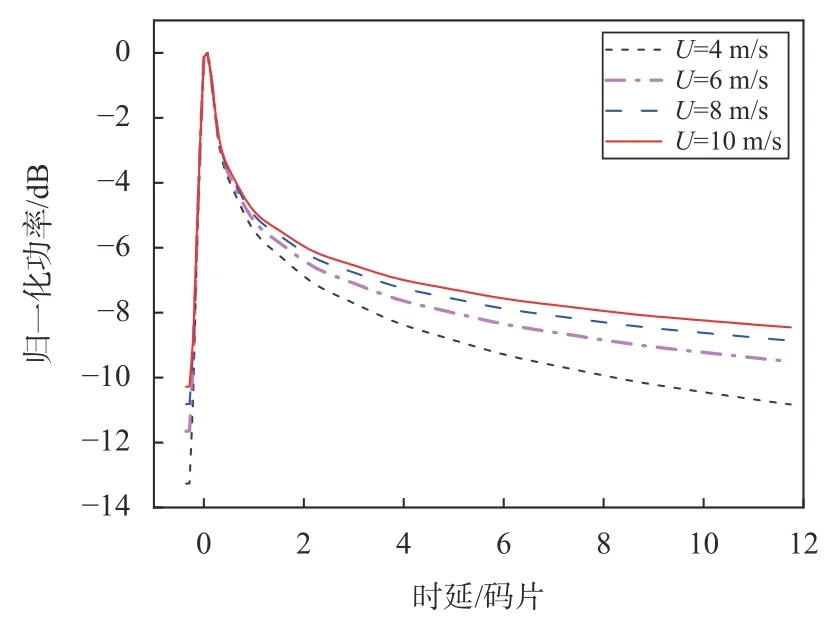
圖5 時(shí)延一維相關(guān)功率曲線

2.3 時(shí)延-多普勒二維相關(guān)功率

式(6)可表示為二維卷積形式

式(12)可通過二維傅里葉變換加速計(jì)算.在式(12)中，χ2(τ,fd)是模糊函數(shù)，χ可理解為來自單個(gè)延遲-多普勒單元的散射信號(hào)的脈沖響應(yīng).Σ由式(13)給出

GNSS 反射信號(hào)的時(shí)延-多普勒二維相關(guān)功率可視為海面閃耀區(qū)內(nèi)散射信號(hào)相關(guān)功率在時(shí)延和多普勒兩個(gè)維度上的映射，也稱為DDM.由式(12)可知，DDM 可由(τ,fd)域上的二維卷積完全確定，故只需在時(shí)延-多普勒坐標(biāo)系下考慮式(12)，而無需關(guān)注模擬的物理表面的實(shí)際大小.

為了得到DDM，先進(jìn)行一個(gè)變量變換，將其從空間域(x,y)轉(zhuǎn)換到時(shí)延-多普勒域(τ,fd)

式(13)中的表面微分d2ρ變?yōu)?/p>

式中： dfd,xy和dτxy為新積分變量的微分；|J|為式(14)中變量變換的雅可比矩陣的行列式.雅可比矩陣說明了物理空間與延遲-多普勒空間的對(duì)應(yīng)關(guān)系.

等時(shí)延線和等多普勒線將反射面劃分成了大量的反射面元，而時(shí)延間隔和多普勒間隔的大小決定了這些反射面元的大小，如圖6 所示.

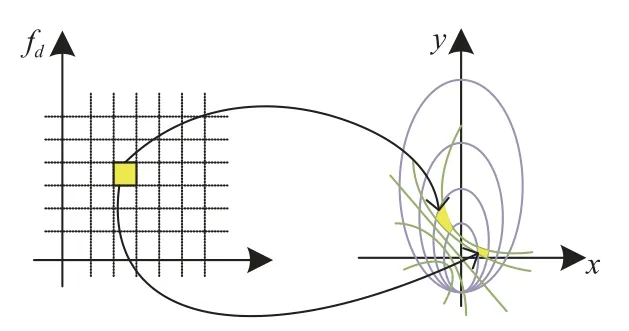
圖6 反射面單元與時(shí)延-多普勒單元映射圖

GNSS 反射信號(hào)由于傳播特性和海面粗糙性，總體表現(xiàn)為信號(hào)幅度的衰減，且相對(duì)于直射信號(hào)，反射信號(hào)有不同的時(shí)延和多普勒頻移.GNSS 海面反射信號(hào)是不同海面散射單元的散射信號(hào)共同作用的結(jié)果.利用等延遲線和等多普勒線將海面散射單元?jiǎng)澐殖梢粋€(gè)個(gè)小反射面元，這些小面元在時(shí)延和多普勒兩個(gè)維度上的功率疊加起來即是反射信號(hào)的DDM.反射面單元與時(shí)延-多普勒單元的映射關(guān)系如圖6 所示.

3 結(jié)果與分析

為分析時(shí)延間隔對(duì)海面反射面元的影響，圖7 仿真了在多普勒頻移一定時(shí)，時(shí)延間隔分別為0.25、0.50 和1.0 個(gè)碼片的反射信號(hào)海面散射單元的劃分區(qū)域顯示.在圖7 中，接收機(jī)高度為682km，GNSS衛(wèi)星高度角為60°，風(fēng)速為10m/s，多普勒間隔固定為500Hz.

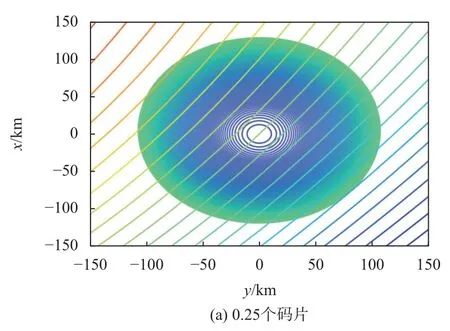
圖7 不同時(shí)延間隔的海面散射單元?jiǎng)澐?/p>

當(dāng)多普勒頻移一定時(shí)，時(shí)延間隔越小，等延遲線和等多普勒線相交的反射面面元越小.由圖7 可知，整個(gè)環(huán)形區(qū)的寬度及環(huán)的厚度取決于時(shí)間延遲τ和雙基幾何結(jié)構(gòu)，而環(huán)形區(qū)的寬度攜帶了有關(guān)海浪坡度或近海面風(fēng)的信息.

當(dāng)時(shí)延保持不變時(shí)，多普勒頻移間隔的大小對(duì)于DDM 波形的仿真結(jié)果有一定影響.圖8 展示了兩種情況下的評(píng)估結(jié)果.仿真中涉及到的主要輸入?yún)?shù)如表1 所示.

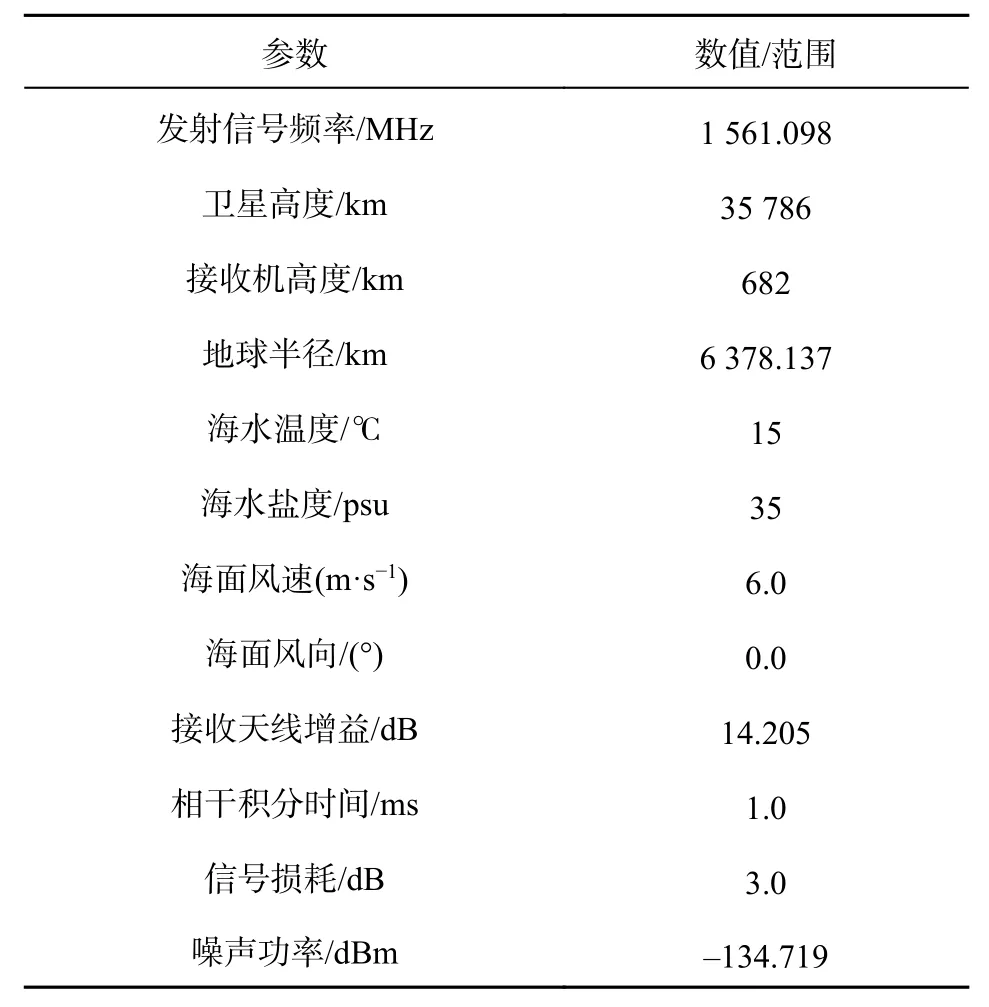
表1 主要輸入?yún)?shù)

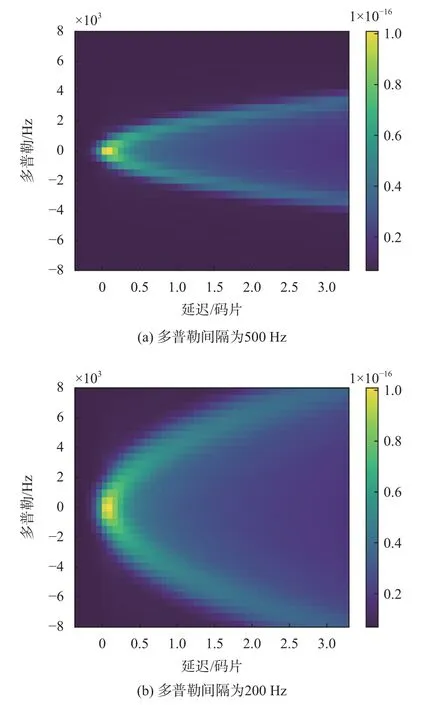
圖8 不同多普勒間隔下的DDM 波形

圖8 給出了不同多普勒間隔下的DDM 波形.由圖8 可知，二維時(shí)延-多普勒相關(guān)功率呈經(jīng)典的“馬蹄”狀分布.其中圖8(a)是多普勒間隔為500Hz 時(shí)的DDM 波形.圖8(b)的多普勒間隔為200Hz，對(duì)比圖8(a)和圖8(b)可知，多普勒頻移間隔越小，仿真得到的DDM 波形分辨率越高.由圖8 可以發(fā)現(xiàn)，DDM最大相關(guān)功率位于時(shí)延和多普勒為零處，也就是鏡面反射點(diǎn)的位置.鏡面反射點(diǎn)是發(fā)射機(jī)-地球表面-接收機(jī)之間距離最短的點(diǎn)，是測(cè)量和建模的主要參考點(diǎn).通過對(duì)比圖4 和圖8 可以發(fā)現(xiàn)，DDM 具有很強(qiáng)的中心瓣和較弱的旁瓣，恰好反映了GNSS 信號(hào)的伍德沃德模糊函數(shù)的結(jié)構(gòu)特征.

DDM 波形中的每一個(gè)單元表示GNSS-R 海面反射信號(hào)在特定時(shí)延和多普勒頻移下的強(qiáng)度，或者說相關(guān)功率.通過觀察DDM 波形，可以得到反射信號(hào)在時(shí)延和多普勒頻率上的功率分布情況.DDM 對(duì)于分析海面目標(biāo)的散射特性具有重要意義，在GNSS-R的研究和應(yīng)用中起著重要作用.

4 結(jié)束語

本文在經(jīng)典Z-V 模型的基礎(chǔ)上，研究了GNSS海面反射信號(hào)特性，所使用的建模方法不僅可以仿真時(shí)延一維相關(guān)功率，而且可以模擬反射信號(hào)的DDM.討論了不同風(fēng)速下的相關(guān)功率變化情況，數(shù)值結(jié)果表明，時(shí)延一維相關(guān)功率對(duì)風(fēng)速具有敏感性.研究了時(shí)延間隔對(duì)海面散射單元的影響，結(jié)果表明，時(shí)延間隔越大，等延遲線和等多普勒線相交的區(qū)域越大.分析了多普勒間隔對(duì)時(shí)延-多普勒二維相關(guān)功率即DDM的影響，結(jié)果表明，多普勒間隔越小，DDM分辨率越高，海面散射單元?jiǎng)澐衷叫。S相關(guān)功率的計(jì)算越精確.且在時(shí)延間隔不變的情況下，多普勒間隔變小，海面散射區(qū)域尾部逐漸展寬.因經(jīng)典的Z-V 模型中海面散射模型基于物理光學(xué)的幾何光學(xué)極限，故該模型不適用于低掠入射角場(chǎng)景.為此，后續(xù)將基于更合理的海面散射模型開展海面GNSS 散射信號(hào)建模及應(yīng)用研究.