非周期二進制/M 進制信號激勵下非線性系統的非周期共振研究*

王重秋 楊建華

1) (中國礦業大學計算機科學與技術學院,徐州 221116)

2) (中國礦業大學機電工程學院,江蘇省礦山機電裝備重點實驗室,徐州 221116)

研究單一非周期二進制或M 進制信號激勵下一類非線性系統的非周期共振現象及其度量方法,重點探討了系統參數引起的非周期共振.提出了適用于非周期共振度量的響應幅值增益指標,并結合互相關系數和誤碼率展開研究.結果發現,互相關系數能夠較好地描述系統輸出和輸入信號之間的同步性及波形相似性但無法刻畫信號通過系統后被放大的程度.響應幅值增益能夠較好地描述信號通過系統后幅值被放大的程度,但無法反映系統輸出和輸入信號之間的同步性及波形相似性.非周期共振發生在互相關系數取谷值和響應幅值增益取峰值處,且兩種指標曲線反映的共振點相同.誤碼率在合適的閾值下可以描述系統輸出和輸入信號之間的同步性以及非周期信號通過系統后被放大的程度,誤碼率曲線可以直接給出非周期共振的共振區.單一非周期二進制或M 進制信號激勵下的非線性系統可以發生非周期共振,其共振效果需要綜合互相關系數、響應幅值增益、誤碼率等指標進行度量.

1 引言

非周期信號廣泛存在于自然界和工程領域.非周期二進制信號是非周期信號的一種典型形式,在通信技術[1]、激光物理[2,3]、圖像處理[4,5]等領域廣泛使用.已有的研究文獻對周期信號激勵下非線性系統的響應研究較多,如隨機共振[6–10]、振動共振等現象[11–13].非周期信號激勵下,非線性系統響應呈現復雜的動力學行為,典型的現象有非周期隨機共振[14–16]、非周期振動共振[3,17,18]等,這些非線性現象及機理為非周期信號處理提供了新的途徑.

Duan 等[19]在離散的Hopfield 神經網絡中研究了非周期二進制信號的傳輸問題,基于非周期隨機共振提高了信號傳輸效率.Kang 等[20]研究了色噪聲和非周期二進制信號激勵下神經元系統的信息處理過程,基于系統響應的非周期隨機共振理論,發現了噪聲在非周期信號處理過程中的積極作用.Zhao 等[21]和Huang 等[22]基于陣列非周期隨機共振進行了圖像降噪自適應處理,提高了噪聲背景下圖像的處理信噪比和處理效率.非周期M進制信號是非周期二進制信號的拓展形式,其在工程領域應用同樣廣泛.M進制信號激勵下非線性系統的非周期共振呈現更復雜的共振形式.Zeng 等[23]和Liang 等[24]分別研究了不同噪聲背景下M進制信號的隨機共振及信號檢測問題,探索了噪聲的積極作用.McDonnell 和Gao[25]研究了M進制信號激勵下系統的超閾值隨機共振,研究結果對多傳感器的信號處理具有參考價值.Cheng 等[26]研究了信號相關噪聲激勵下多級閾值系統中的超閾值隨機共振,研究結果有助于理解生物感覺系統的編碼機制.在更廣泛的范圍內研究非周期信號激勵下系統的隨機共振,有利于解決旋轉機械設備故障診斷[27]、磁場異常檢測[28]、鋼絲繩無損探傷[29]等領域的工程問題.

非周期二進制信號激勵下的非線性系統,如果同時加入高頻激勵信號,系統響應會發生非周期振動共振現象[17].Chizhevsky 等[3,30]在基于非周期振動共振的激光系統微弱二進制信號檢測方面做了較多的工作.Morfu 等[31,32]基于非周期振動共振進行圖像處理研究,通過非周期振動共振進一步提高了含噪圖像處理的效果.關于非周期二進制信號激勵下系統的振動共振理論研究尚多,比如適用于快變非周期信號的變尺度方法以及二次采樣方法[17,18],非周期振動共振的應用研究尚處于起步階段.非周期M進制信號激勵下非線性系統振動共振響應的文獻尚未發現.

不管是非周期隨機共振還是非周期振動共振的研究文獻,側重點往往是激勵中的噪聲或者起輔助作用的高頻信號,側重于由這兩種因素引起的非周期共振現象.事實上,在非周期共振的研究中,非線性系統一般會起到更重要的作用.對于激勵中不含有噪聲或者高頻輔助信號的情況,系統對單一信號的響應是否存在較強的非周期共振是非常值得探討的問題.目前對于周期信號和調頻信號激勵下系統參數引起的共振已有相關研究成果[33–35].對于單一非周期二進制信號或M進制信號是否會引起系統輸出的非周期共振響應尚無相關研究.只有弄清這一問題,才能為非周期二進制或M進制信號處理時選擇非線性系統提供依據,開拓新思路和新方法,同時也能發現新的非線性動力學現象,拓展非線性動力學的研究成果.

本文結構安排如下: 第2 部分研究非線性系統對非周期二進制信號的響應,基于三種不同的指標探討系統參數引起的非周期共振現象,并對每個指標的度量效果進行對比分析;第3 部分研究非線性系統對非周期M進制信號的響應,基于動力學響應的復雜性分析該種激勵下非線性系統發生非周期共振的條件;第4 部分給出本文的結論.

2 非周期二進制信號引起的非周期共振

研究非周期信號激勵下的過阻尼非線性系統

其中a和b為系統參數,s(t) 是非周期激勵信號,本文分別考慮s(t) 為非周期二進制信號和非周期M進制信號兩種情況.參數a,b取值不同,系統勢函數具有不同的不動點,勢阱形狀呈現不同的穩態模式[36].

2.1 非周期二進制信號

非周期二進制信號的表達式為

其中A是信號 的振幅,Rm=1或-1 是符合 一定統計規律的隨機數,本文采用符合高斯分布的隨機數.函數Γ(t) 滿足

其中,T是脈寬,即非周期信號s(t) 隨機脈沖的最小寬度.

由于信號s(t) 的非周期性,導致信號具有一定的隨機性,圖1 給出了在幅值A和脈寬T取值一定時s(t) 的3 種不同波形.為方便描述,圖中的3 種波形對應的信號自上而下依次命名為Signal 1,Signal 2,Signal 3,(1)式中Rm序列的不同導致信號波形的不同.

圖1 A=0.3,T=100 時,非周期二進制信號的不同時域波形.自上而 下信號 分別標記為Signal 1,Signal 2,Signal 3Fig.1.Different waveforms of the aperiodic binary signal at A=0.3,T=100.The signals are labeled as Signal 1,Signal 2,Signal 3 from top to bottom.

2.2 非周期共振分析

在研究非周期二進制信號引起的隨機共振和振動共振現象時,一般以系統輸出x(t) 和輸入信號s(t)之間的互相關系數作為指標.互相關系數為

其中m為時間序列的總長度,sˉ和xˉ 分別為時間序列的均值.

針對圖1 中給出的3 種信號,圖2 給出了互相關系數Csx和系統參數a之間的關系曲線.從圖2可見,信號波形的差異不會導致互相關系數曲線的本質變化.也就是說,在圖1 給定的3 種信號下,圖2中Csx-a的變化規律基本一致.因此,后續分析采用一種波形信號即可.圖2 中隨著系統參數a的變化,相關系數呈現明顯的變化趨勢.在a從負值到正值變化的過程中,相關系數減小,并在a=1.05處達到極小值.之后,隨著a值的進一步增大,在a=1.1 處達到峰值.事實上,互相關系數只能描述兩個時間序列的同步性及波形的相似性,并不能刻畫信號通過系統之后是否被放大.因此,還需要借助于時間序列或者其他指標進一步分析.

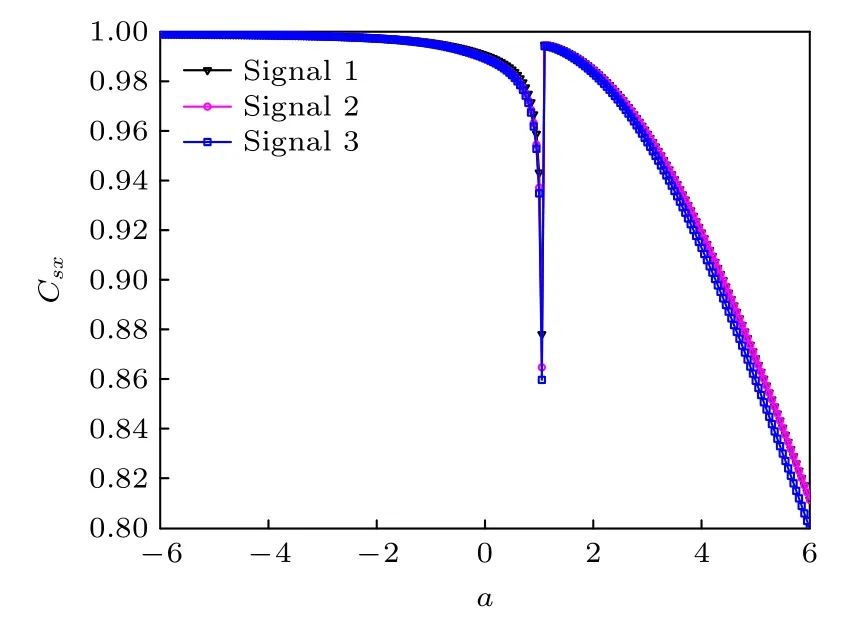
圖2 b=2,A=0.3,T=100 時,不同波形的非周期二進制信號激勵下,系統輸出與輸入信號之間的互相關系數Csx 與系統參數a 之間的關系Fig.2.Cross-correlation coefficient Csx between the system output and input signal versus the system parameter a under the excitation of aperiodic binary signal with different waveforms at b=2,A=0.3,T=100.

圖3 給出了系統參數a取值不同時,系統響應的時間序列.從時間序列上看,每一幅子圖上輸出和輸入的波形相似性較大,這是圖2 中相關系數取值較大的原因.此外,相關系數小于1 的原因是系統的輸出和輸入之間存在一定的相位滯后,造成在時域上輸出波形的變化和輸入波形的變化并不完全同步.在圖3(a)和圖3(b)中,即當a=0 和a=1.05 時,系統輸出呈現非周期共振狀態,輸出信號相較于輸入信號被放大.圖3(b)中的共振最強,對應于圖2 中相關系數取極小值,即相關系數曲線取谷值的情況.在圖3(c)和圖3(d)中,雖然輸出信號和輸入信號之間的相似性仍較高,但其響應幅值未被系統放大.圖3(c)的參數取值對應于圖2 中相關系數取峰值的情況.圖中反映的結果和之前類似的研究是不同的,比如在之前隨機共振和振動共振的研究中,最強的共振往往出現在相關系數取峰值的情況[3,14–18].

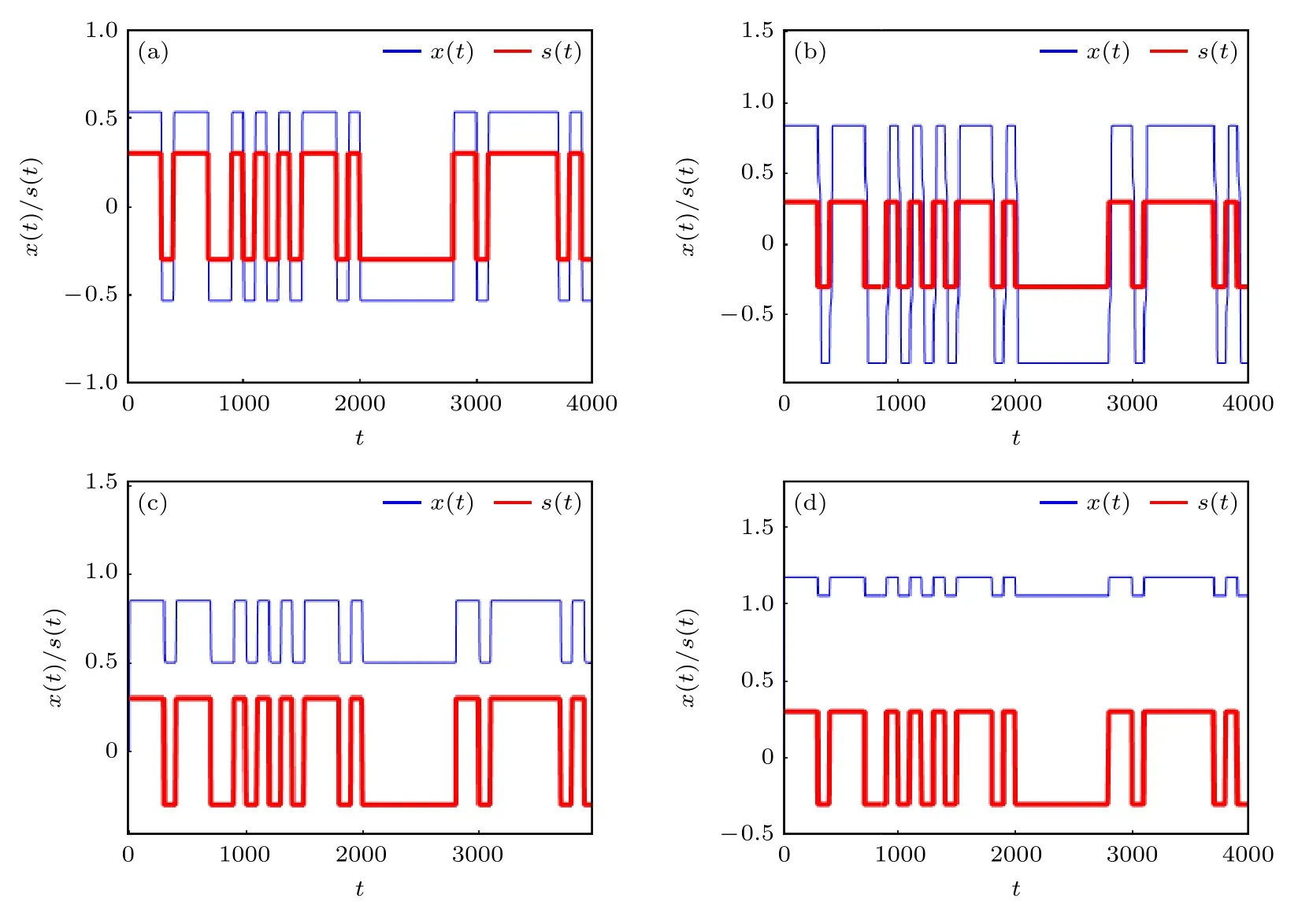
圖3 b=2,A=0.3,T=100 時,系統參數a 取值不同時輸出的不同波形 (a) a=0 ;(b) a=1.05 ;(c) a=1.1 ;(d)a=2Fig.3.Different waveforms of the output under different values of the system parameter a with b=2,A=0.3,T=100:(a) a=0 ;(b) a=1.05 ;(c) a=1.1 ;(d) a=2 .

從以上圖2 和圖3 的分析中發現,基于相關系數很難直接反映信號被放大即系統響應發生非周期共振的情況,時間序列也僅能從有限的算例直觀反映系統的輸出,不能給出通用性更強的結論.為了更好地刻畫非周期共振,需要新的指標.因此,此處提出響應幅值增益指標,其計算公式為

其中符號max 和min 分別表示取最大值和最小值.結合圖2 中的時間序列容易理解(5)式的物理意義,其中可以直觀理解為響應的幅值,很明顯β 為系統輸出和輸入信號之間幅值的比值.值得一提的是,在計算β 時,x(t)應該截掉初始條件x(0) 引起的瞬態響應,否則影響輸出的準確性.雖然(5)式中計算響應幅值增益指標具有一定的近似性,但其在大部分情形下能從本質上說明信號通過系統后振幅被放大的倍數.

根據(5)式的計算公式,圖4 給出了系統的響應幅值增益β 與系統參數a之間的函數關系曲線,圖中很好地顯示了系統的共振以及信號幅值被放大的情況.圖中共振發生在a=1.05 處,此時β=2.8,說明非周期二進制信號通過系統后幅值被放大了2.8 倍.進一步地,共振點對應的位置a=1.05也對應于圖2 中相關系數取極小值點,即取谷值的點.對比響應幅值增益和相關系數曲線呈現的規律,相關系數主要是反映輸出和輸入之間的同步性,并從側面對共振的分析提供參考;響應幅值增益直接反映系統輸出和輸入信號之間的幅值變化情況,不能直接反映系統輸出和輸入信號之間的波形是否同步變化,假設系統輸出和輸入之間存在較大的滯后甚至反相,不會影響幅值增益β 的值,但會明顯影響相關系數Csx的值.因此,互相關系數和響應幅值增益僅各從一個角度反映系統輸出的情況.

圖4 b=2,A=0.3,T=100 時,響應幅值增益β 與系統參數a 之間的函數關系Fig.4.Response amplitude gain β versus the system parameter a with b=2,A=0.3,T=100.

為了更好地揭示系統輸出x(t) 隨系統參數a的變化情況,此處引入另一個指標,即誤碼率(bit error rate,BER),誤碼率也可以用于描述系統的共振行為[37].對于誤碼率的計算,如何定義輸出被正確接收和錯誤接收的碼元將直接影響誤碼率的值.眾所周知,系統輸出幅值一般不等于輸入信號的幅值.如果輸出的幅值絕對值大于給定的閾值Ath就認為碼元接收正確,反之則錯誤.因此,閾值Ath的選擇也至關重要.不同的閾值對應不同的物理意義,此處分別選擇兩種典型的閾值,即Ath=0和Ath=A.顯然,Ath=0 意味著輸出和輸入之間的正負一致,這確保了輸出和輸入信號之間的同步性.在此基礎上,如果再滿足Ath=A,就能夠保證系統輸出和輸入在同步的基礎上幅值被放大.基于這種計算思想,圖5 給出了在兩種不同閾值Ath情況下,誤碼率BER 與系統參數a之間的函數關系曲線.圖5 中關于參數a的數值計算步長為 0.05 .對應于Ath=A,當a≤-0.85時BER=1,這說明信號完全沒有被放大;而對應于Ath=0 ,BER=0,說明輸出波形和輸入波形完全同步.在a∈[-0.8,1.05] 區間上,對應于Ath=A和Ath=0 的兩條曲線值接近,且都接近于0,這說明在這段區間上系統能夠發生較強的非周期共振現象,即輸出能夠保持和輸入信號波形的相似性又能夠被放大.對于a＞1.1 的情況,兩條曲線重合且誤碼率保持為0.45,這說明一部分信號被放大而另一部分信號被錯誤接收,如圖3(c)和圖3(d)的輸出情形.在誤碼率曲線上,a∈[-0.8,1.05] 被認為是比較強烈的非周期共振區間.對于a≥1.1 的情況,兩條誤碼率曲線幾乎完全重合,這主要是由于輸出向一個勢阱內漂移并在一個勢阱內振蕩,使輸出和輸入之間的正負不再完全同步,導致BER 取相對較大的值.

圖5 b=2,A=0.3,T=100 時,誤碼率BER 與系統參數a 之間的函數關系Fig.5.Bit error rate (BER) versus the system parameter a with b=2,A=0.3,T=100.

互相關系數、響應幅值增益、誤碼率在反映非周期共振方面都有一定的適用范圍和相應的優勢,這3 種指標也能反映一定的共性規律,比如3 種函數指標曲線都顯示當a=1.05 時系統輸出會呈現較強烈的非周期共振現象.

3 非周期M 進制信號引起的非周期共振

3.1 非周期M 進制信號

非周期M進制信號為s(t)=Am,m=1,2,···,s(t) 在每個 碼元的 振幅為Am=(2m-1-M)A,且服從給定的概率分布,此處令Rm滿足均勻分布.當(2)式中的隨機數Rm的選擇范圍從 -1和1 擴大到 2m-1-M中的任意數時,非周期二進制信號擴展為非周期M進制信號.在信號參數取值一定時,圖6 中給出了M進制信號3 種不同的波形.在本部分,圖中的3 種波形對應的信號自上而下命名為Signal 4,Signal 5,Signal 6.

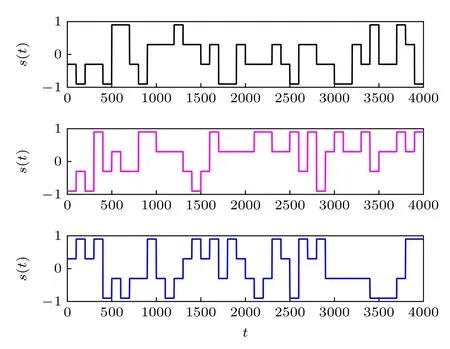
圖6 M=4,b=2,A=0.3,T=100 時,非周期M 進制信號的不同時域波形.自上而下信號分別標記為Signal 4,Signal 5,Signal 6Fig.6.Different waveforms of the aperiodic M-ary signal with M=4,b=2,A=0.3,T=100.The signals are labeled as Signal 4,Signal 5,Signal 6 from top to bottom.

3.2 非周期共振分析

針對圖6 中給出的3 種信號,圖7 給出了互相關系數Csx和系統參數a之間的關系曲線.由于輸入信號波形的差異,導致相關系數最小值的具體取值存在一定差異,這和信號長度選取有關,當信號選取足夠長時這種差異可以消失.相關系數最小值的微小差異不影響其對應的系統參數a取值,不影響系統參數引起的非周期共振基本規律.圖7 說明非周期M進制信號波形的不同不會導致Csx與a之間關系曲線的本質變化,因此本部分對M進制信號的共振分析以一種信號波形為例即可.以Signal 4 為例,分析相關系數隨著a的變化趨勢,在a=2.2 處相關系數達到極小值,即谷值,在a=3處相關系數達到峰值.

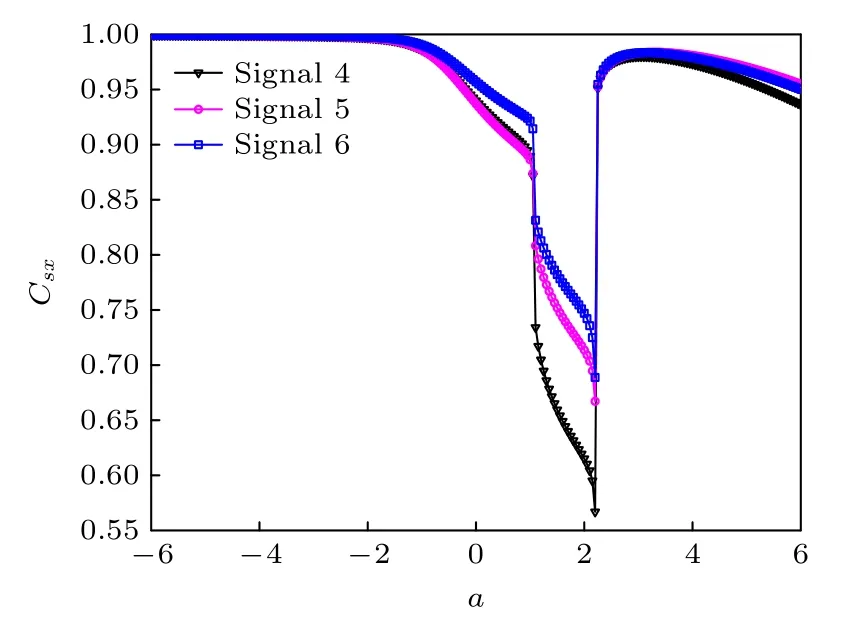
圖7 M=4,b=2,A=0.3,T=100 時,不同波形的非周期M 進制信號激勵下,系統輸出與輸入信號之間的互相關系數 Csx 與系統參數a 之間的關系Fig.7.Cross-correlation coefficient Csx between the system output and input signal versus the system parameter a under the excitation of aperiodic M-ary signal with different waveforms at M=4,b=2,A=0.3,T=100.

為了進一步探究系統輸出的共振情況,圖8 給出了系統參數a取值不同的情況下系統輸出的波形.參數a的取值主要參考了圖7 中對應相關系數的取值情況.圖8(a)對應于圖7 中相關系數曲線到達極小值之前的情形,時間序列反映了輸出和輸入之間存在一定的同步性,但部分信號幅值不僅沒有被放大,反而比之前的幅值小.圖8(b)對應于圖7 中的曲線極小值,對應的時間序列是圖8 的4 幅子圖中非周期共振效果最強的.圖8(c)對應于圖7 中的曲線峰值,此時雖然輸出和輸入信號的波形相似性較好,但輸出被限制在一個勢阱之內,輸出的幅值較小.在圖8(d)中,輸出仍然被限制在一個勢阱之內,信號幅值進一步縮小.相較于非周期二進制信號的情形,非周期M進制信號激勵下非線性系統的輸出呈現更加復雜的特性,輸出難以達到既和輸入信號波形相似又被放大的效果.

圖8 b=2,A=0.3,T=100 時,系統參數a 取值 不同時輸出的不同波形 (a) a=0 ;(b) a=2.2 ;(c) a=3 ;(d)a=5Fig.8.Different waveforms of the output under different values of the system parameter a with b=2,A=0.3,T=100: (a) a=0 ;(b) a=2.2 ;(c) a=3 ;(d) a=5 .

參照(5)式計算響應幅值增益的方法,將(5)式改造為可以計算M進制信號引起的響應幅值增益的公式

從系統的輸出時間序列(如圖8 中的時間序列)可以發現,系統的輸出不再是M個碼元,而是會進一步增加碼元的個數,因此響應幅值增益改進為(6)式的形式.顯然,由于輸出中碼元的增多以及各碼元的相對位置變化較大,(6)式是一種均值意義上的估計,能夠大致反映M進制信號輸入系統后對應的輸出被放大的程度.

圖9 給出了響應幅值增益與系統參數a之間的函數關系,β-a曲線呈現明顯的共振現象.共振發生在a=2.2 處,對應于圖7 中相關系數曲線的極小值即波谷位置,這說明通過互相關系數和響應幅值增益反映的共振點是一致的.圖9 的響應幅值增益曲線能夠更好地反映信號通過系統后被放大的情況,圖中的峰值處β=1.35,這說明信號通過系統后發生非周期共振后信號在一定程度上被放大,但信號幅值并不會在很大程度上被放大.

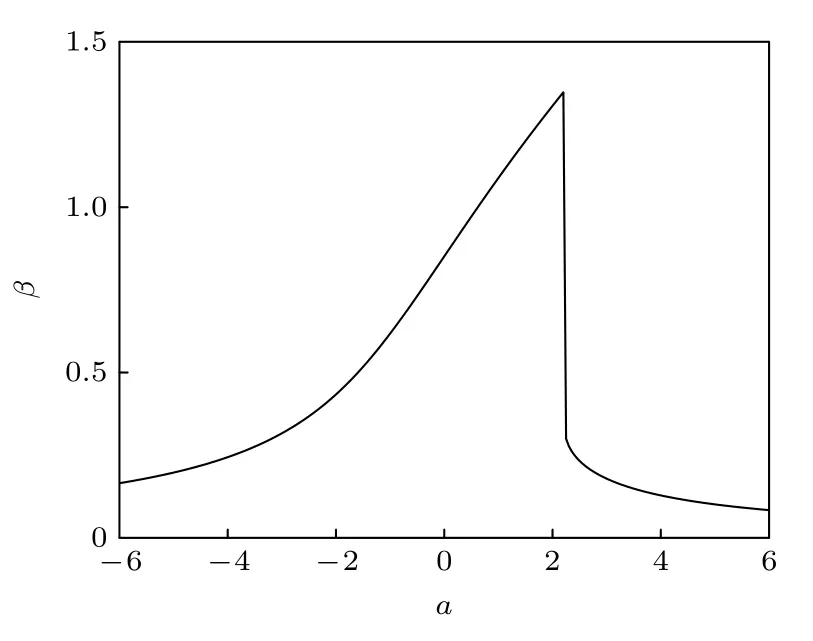
圖9 M=4,b=2,A=0.3,T=100 時,響應幅值增益β 與系統參數a 之間的函數關系Fig.9.Response amplitude gain β versus the system parameter a with M=4,b=2,A=0.3,T=100.

以誤碼率為計算指標,圖10 為誤碼率BER與系統參數a之間的關系曲線.對應于Ath=0 的誤碼率曲線刻畫了輸出和輸入之間同步變化的情況,對應于Ath=A的誤碼率曲線既刻畫了輸出和輸入之間同步變化又刻畫了信號通過系統后被放大的情況.曲線Ath=A取小值的區間是非周期共振較強烈的區間,比如圖7中a∈[0.65,1.05] 的區 間.當a≥0.65 時,對應于Ath=A和Ath=0 的曲線基本重合.a取值在0 和1 之間,誤碼率曲線呈現階梯狀水平線,這既說明系統輸出和輸入信號之間的波形存在一定的相似性,又說明系統輸出中僅部分信號相較于輸入信號的幅值被放大.

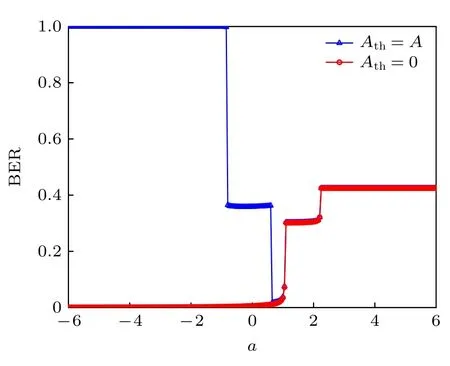
圖10 M=4,b=2,A=0.3,T=100 時,誤碼率BER 與系統參數a 之間的函數關系Fig.10.Bit error rate BER versus the system parameter a with M=4,b=2,A=0.3,T=100.

為了進一步明確顯示系統發生非周期共振時的系統輸出情況,對應于圖10 中的共振區選擇不同的a值,圖11 給出了對應的響應時間序列.圖11的時間序列,相較于圖8(b)—(d),輸出呈現出更明顯的同步性,輸出能夠在兩個勢阱之間隨著輸入同步翻轉.圖8(b)中有一小部分輸出不能實現和輸入信號在兩個勢阱間同步穿越,導致共振效果欠佳.圖8(c)中的輸出幾乎都被限制在一個勢阱內,共振效應進一步下降.對應于圖10 中的共振區中的參數取值,圖11 中的時間序列不存在上述問題,輸出和輸入之間的同步性較好,信號在一定程度上被放大.從圖11 的時間序列進一步發現,M進制信號激勵下系統的非周期共振更側重于對輸入和輸出之間同步性及碼元接收正確性的一種描述,不再側重于信號的放大效應.

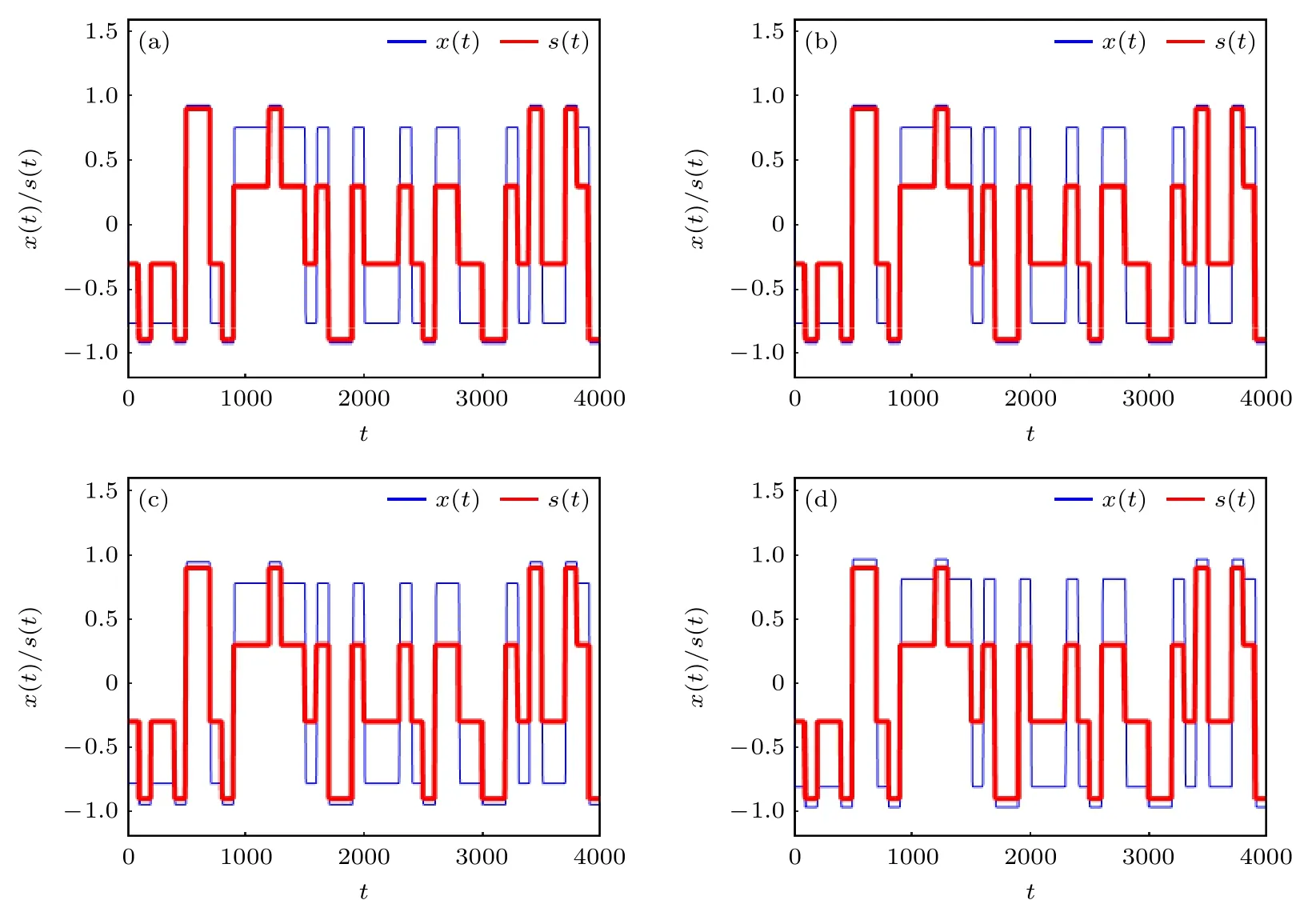
圖11 M=4,b=2,A=0.3,T=100 時,系統參 數a 處于共 振區時 輸出的波形 (a) a=0.65 ;(b) a=0.75 ;(c) a=0.85 ;(d)a=0.95Fig.11.Different waveforms of the output when the system parameter a lies in the resonance region with M=4,b=2,A=0.3,T=100: (a) a=0.65 ;(b) a=0.75 ;(c) a=0.85 ;(d) a=0.95 .

對比非周期二進制信號引起的共振和非周期M進制信號引起的共振,發現系統參數的變化均能引起非周期共振現象,且兩種信號引起的非周期共振程度可以用相同的指標進行描述,反映共振規律的曲線具有相似的特點.然而,非周期二進制信號引起的共振能夠達到更強的共振程度,而非周期M進制信號引起的共振程度相對較弱.這是因為非周期二進制信號波形相對簡單,經過系統后雖然輸出信號幅值發生了變化,但一般情況下仍保持為非周期二值信號,而非周期M進制信號經過系統后一般會增大M的值,即輸出信號取值多于M個值,這就造成了輸出信號波形難于和輸入的M進制信號匹配,因而從度量指標和輸出波形上反映的共振程度較弱.

4 結論

分別以非周期二進制信號和非周期M進制信號作為輸入信號,研究單一非周期信號激勵下非線性系統的響應行為,重點討論非周期共振現象及其度量方法.研究主要得到了以下結論:

1)在單一的非周期二進制信號或者非周期M進制信號激勵下,通過調整系統參數,非線性系統的輸出能發生非周期共振.當非周期共振發生時,系統輸出和輸入信號之間保持較好的同步性,即系統輸出在勢阱內的穿越和輸入信號的正負變化也同步,且系統輸出的幅值比輸入信號幅值增大.

2)為了更好地度量非周期共振效果,分別采用了互相關系數、誤碼率作為指標,并提出了響應幅值增益指標.互相關系數指標能夠較好地刻畫輸出和輸入之間同步性與波形相似性,無法直接判斷輸出是否發生了非周期共振,但可以輔助判斷非周期共振的發生.針對采用的兩種形式的非周期信號,非周期共振點均在互相關系數取極小值即波谷的位置.響應幅值增益指標可以直接刻畫系統輸出的幅值相較于輸入信號幅值被放大的情況,但無法描述系統輸出和輸入信號之間的同步性或波形相似性.以誤碼率作為非周期共振的度量指標,選擇合適的閾值,誤碼率曲線既能反映系統輸出和輸入信號的同步性和波形相似性,也能描述信號的放大性,并在曲線上呈現明顯的共振區.

3)從共振效果上看,非周期二進制信號引發的非周期共振比非周期M進制信號引發的共振更強烈,這是由非周期M進制信號本身的復雜性以及通過系統后輸出的復雜性導致的.

不論是比較簡單的非周期二進制信號還是更復雜的非周期M進制信號引起的非線性系統響應,如果要明確地描述系統的非周期共振現象,應該選擇多個指標從多個角度進行描述,同時考慮不同指標對非周期共振效果的影響.通過選擇不同的非線性系統、采用優化算法實現適應度函數最優化、綜合考慮非周期隨機共振、振動共振、系統共振等多種共振模式,有望進一步提高系統的共振效果.本文雖然只考慮了系統參數對非周期共振的影響,但發現了單一非周期信號激勵下非線性系統的非周期共振這種之前未被明確提出的新現象,并對非周期共振效果的度量給出了多個指標和多種方法.以本文的研究為基礎并通過進一步拓展,還可以深入探討不同非線性系統以及更多形式的非周期信號引起的非周期共振新現象、提高共振效果的新方法、以及在不同物理背景下的新應用.