基于G 代碼修改的數控機床運動誤差修正方法

聶 娜

（山東省菏澤信息工程學校，山東 菏澤 274000）

0 引言

當前隨著現代機械制造技術的發展，數控機床加工被應用到眾多領域當中，對其精度的要求也進一步提高。在數控機床中，運動誤差是衡量其精度的一個重要指標，它對工件的加工精度有很大的影響。有很多因素會導致運動誤差，如何將其識別出來，如何在機床設計、制造及使用中，對其進行快速、準確的追溯，已成為亟待解決的難題[1]。目前，常見的提升數控機床運動精度的方法包括兩種，一種為誤差防止，另一種為誤差補償修正。預防錯誤的措施是在設計、制造、裝配、運輸過程中盡量降低或消除錯誤源，但是在實踐中，隨著加工精度的提高，僅僅通過預防錯誤的方法來減少或消除錯誤，將使生產成本大大增加，而且其技術難度也隨之提升了不少[2]。因而，僅靠預防誤差的方法已難以滿足現代數控機床對高精度運動的需求。

綜合上述分析，針對數控機床的運動誤差補償修正是實現高精度數控機床運動、改善數控機床性能的重要途徑。相關領域研究人員也對其進行了深入的探索研究，先后出現了三角關系幾何法、矢量法等多種數控機床運動誤差補償修正的理論研究。但目前，以上方法在實際應用中都會存在一些問題，限制其進一步的廣泛運用，例如構建的誤差模型不具備通用性、運算量大、操作復雜等。因此，針對當前現有誤差修正方法存在的問題，引入G 代碼修改，開展對數控機床運動誤差修正方法的設計研究。

1 構建數控機床運動誤差模型

為了得到一種具有普適性的誤差模型，基于多體系統理論以及齊次坐標變換理論，將機床分成兩個部分，分別得到了兩個部分，一個是刀具，另一個是工件。分別建立在理想狀態下和存在誤差狀態下刀具與相應工件的位置表達函數，并以此得到數控機床運動誤差模型。將數控機床基本結構作為核心，將其劃分為刀具分段和工件分段兩個組成部分[3]。其中刀具分段是從數控機床身開始到刀具；工件分段是從數控機床身到工件段。結合多體系統理論分析得出，刀具相對于工件而言，其位置的表達函數為：

根據上述運算邏輯可以進一步推算得出刀具相對于床身、工件相對于床身等之間的位置表達函數[4]。再結合齊次坐標變換理論和小角度誤差假設得出，相鄰的兩個部件之間，其變換矩陣可表示為：

式中：a 和b 為在數控機床上運動的兩個部件；δX為a部件相對于b 部件沿著X 軸運動產生的線性位移；δY為a 部件相對于b 部件沿著Y 軸運動產生的線性位移；δZ為a 部件相對于b 部件沿著Z 軸運動產生的線性位移；εX、εY、εZ分別為a 部件相對于b 部件在沿著X 軸、Y 軸、Z 軸旋轉過程中對應產生的角位移。

將式（1）和式（2）代入式（3），求得空間層面上的數控機床運動誤差模型為：

式中：ηi為空間層面上數控機床運動誤差模型表達函數，i=X、Y、Z；δi為線性誤差。

根據上述論述完成對數控機床運動誤差模型的構建，為后續對運動誤差的補償修正提供條件。

2 基于G 代碼修改的運動誤差補償修正

2.1 直線運動誤差補償修正

結合G 代碼修改的補償修正方式是將數控機床原始點作為補償的參考點，在此基礎上對數控機床運動誤差進行補償。在修正后，其補償點可以表示為：

式中：Pi為補償后的理想運動控制指令值；Pe為通過G 代碼修改后的補償值。

應用G 代碼修改的方式對數控機床沒有特定要求，常見的數控機床中的數控系統均可以通過這種方式進行誤差補償修正。通過將數控機床移動原點的絕對坐標用作補償基準，從而能夠按照式（4）修正G 代碼。本文提出了一種新的求解方法，即相對坐標補償的參考點是前一目標點，在進行空間誤差的計算時，必須以前一目標點的實際位置坐標為基礎，來計算與前一點的幾何誤差，之后再以其理論位置坐標為基礎，來計算空間誤差；由于前一個目標點的指示值已被設定，但實際坐標卻未被設定，從而導致了幾何誤差的計算不夠精確。因此，相對于相對坐標系，所給出的絕對坐標系能有效地消除因真實坐標系的不確定性所引起的誤差。

在上述論述基礎上，針對數控機床在進行直線運動時產生的誤差進行補償修正[5]。根據起點與終點的坐標可以確定直線的具體長度，在修正時設定插補精度為，將起點與終點的直線長度設置為L，通過式（5）計算確定插補點的坐標：

式中：Xi、Yi、Zi為插補點在X 軸、Y 軸和Z 軸上的坐標；i 為插補點序號。

結合上述計算公式，計算得出各個插補點的理想位置坐標。在對G 代碼進行修正時，需要選擇不同的L，用來實現對不同插補精度要求的補償，以此實現對數控機床部件直線運動的誤差修正。

2.2 圓弧運動誤差補償修正

在對數控機床進行圓弧運動時產生的誤差進行補償修正時，需要明確圓弧運動軌跡的起點、終點和圓心坐標。按照上述基本邏輯，確定插補點的坐標為：

根據式（6）確定插補點的具體位置。通過插補點的設置可以使數控機床圓弧運動軌跡與初始在數控系統上設置的軌跡基本一致，實現對誤差的補償修正。在進行對G 代碼的修改時，可以選擇不同的α 用以滿足不同的插補精度需要。根據上述論述，實現對數控機床直線運動和圓弧運動誤差的修正，確保數控機床運動精度得到有效提升。

3 對比試驗

選擇以基于矢量法的誤差修正方法和基于三角關系幾何法的誤差修正方法作為對照A 組和對照B組，將本文上述提出的方法作為試驗組。利用三種修正方法對同一數控機床運動誤差進行修正補償，通過對比補償后的效果，實現對其各自性能的對比。所選用的數控機床型號為DX46350 三軸數控機床，該型號機床在運動時橫軸有效行程為550 mm，縱軸有效行程為750 mm。控制該型號數控機床進行圓弧運動。圖1 為該數控機床在修正前的平面圓弧運動軌跡。

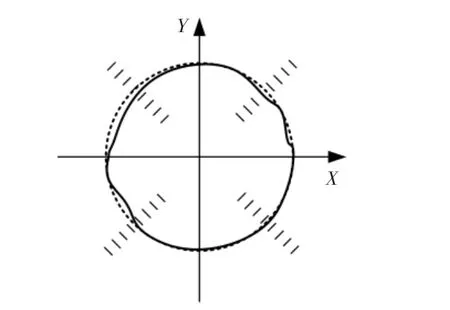
圖1 數控機床修正前平面圓弧運動軌跡示意圖

圖1 中虛線圓表示對該數控機床設置的標準運動軌跡，實線圓表示該數控機床實際完成運動后留下的軌跡。從圖1 可以看出，該數控機床運動存在明顯的誤差，針對這一問題，分別利用上述三種修正方法對其進行修正，并在修正后再次完成上述運動，將運動軌跡記錄，如圖2 所示。

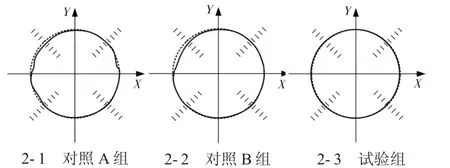
圖2 三種修正方法應用后數控機床平面圓弧運動軌跡

對比圖2 中三種修正方法應用后數控機床平面圓弧運動軌跡可以看出，圖2-1 實際軌跡與標準軌跡相比仍然存在較大的差異，其次為圖2-2，圖2-3 的數控機床實際運動軌跡與標準軌跡基本一致，說明實現了對數控機床運動誤差的有效修正。

4 結語

通過上述研究，結合G 代碼修改，提出了一種全新的針對數控機床運動誤差的修正方法。通過對比試驗的方式證明，新的修正方法在實際應用中具有極高的有效性，將該方法應用到數控機床運動當中可以有效提高運動精度，為數控機床加工質量提升提供技術條件。