一種復雜曲面無基準輪廓度的ER-BFGS評定方法

付高財　盛步云　萬潤　殷希彥　盛甘霖

摘要：針對大量測點導致曲面輪廓度計算耗時倍增的問題，提出一種基于熵正則化和BFGS算法的曲面輪廓度評定方法。該方法在點到曲面的最小距離函數的基礎上，通過熵正則化原理將輪廓度最小區域評定模型的極大極小問題轉化為無約束可微優化問題，并利用快速收斂的BFGS算法進行求解，實現了復雜曲面無基準輪廓度的快速評定。實驗表明該方法在計算耗時方面比序列二次規劃方法縮短約5%～19%，能有效提高在機測量效率。

關鍵詞：在機測量；熵正則化；BFGS算法；面輪廓度

中圖分類號：TH161

DOI：10.3969/j.issn.1004-132X.2023.08.006

An ER-BFGS Evaluation Method for Datum-free Profile of Complex Surfaces

FU Gaocai1 SHENG Buyun1，2 WAN Run3 YIN Xiyan2 SHENG Ganlin4

Abstract： To solve the problem that a large number of measurement points caused the multiplication of time spent in calculating surface profiles， a new surface profile evaluation method was proposed based on ER and BFGS algorithm. Based on the minimum distance function from point to surface， the minimax problem of the profile evaluation model for the minimum region was transformed into an unconstrained and differentiable optimization problem through ER principle， and solved by the fast convergent BFGS algorithm， which realized the rapid profile evaluation of complex surfaces without datum. The experiments show that the calculation time of this method may decrease as 5%～19% compared with the sequential quadratic programming method， and effectively improve the efficiency of on-line measurement.

Key words： on-line measurement； entropy regularization（ER）； BFGS（Broyden-Fletcher-Goldfarb-Shanno）algorithm； surface profile

0 引言

隨著CAD造型技術的發展，幾何特性優越的自由曲面已成為工程上復雜且常用的特征，而評判零件曲面質量是否合格的重要依據是曲面輪廓度是否達到設計的公差要求。依托在機測量技術［1］，這些曲面加工完成后直接在機床上進行質量檢驗，避免了工件搬運、二次裝夾帶來的耗時費力、二次定位誤差等問題。整個在機測量中的測點規劃、測量執行、結果計算等過程不能過多占用機床的運行時間，否則會影響機床的加工利用效率［2］。

曲面輪廓度評定方法主要分為最小二乘法和最小區域法兩大類。最小二乘法［3］雖然原理簡單、工程上易實現，但不滿足ISO標準對最小包容區域的要求。最小區域法完全基于ISO標準的最小條件原則，在無基準曲面輪廓度求解算法中的應用最為廣泛［4］。LANG等［5］在測點到模型表面的距離函數基礎上，建立了基于最小區域準則的最優定位模型，并利用序列二次規劃（sequential quadratic programming，SQP）方法求解出自由曲面的輪廓誤差。ZHANG等［6］引入輔助變量，將不可微極小極大優化問題轉化為帶約束的可微優化問題，并基于原對偶內點法進行最小區域擬合來求解NURBS曲面的輪廓誤差。LIU等［7］提出了一種基于線性四叉樹的表面輪廓誤差粗定位和精確配準算法。ZHANG等［8］借助指數懲罰函數將定位模型優化問題變換為無約束可微最小化問題，采用主動集策略和參數自適應調整的牛頓法計算出輪廓度。TAN等［9］在定位迭代優化過程中引入動態加權策略，采用一種效率高于四元數方法的差分定位算法來快速求解定位的剛性變換參數。為求解符合最小區域要求的輪廓度評定模型，遺傳算法（genetic algorithm，GA）［10］、粒子群優化（particle swarm optimization，PSO）算法［11］、蝙蝠算法［12］和差分進化算法［13］等智能優化算法也在曲面定位參數的求解上有所應用。

雖然SQP、高斯-牛頓等微分方法能有效計算出測點的最優定位參數，但通常都需要引入一些與測點數量相同的額外約束不等式，將評定模型簡化為某類可微優化問題。因此，對于復雜曲面的精密在機測量場景，測點較多時，算法的復雜性將增大，導致測量過程占用大量的機床運行時間，與在機測量技術的初衷相悖。此外GA、PSO等經典智能算法容易陷入局部最優，難以滿足精密測量的需求，且在測量復雜曲面時收斂過慢。

本文針對測點較多的復雜曲面，為避免不可微目標函數而導致復雜算法的問題，采用熵正則化原理將評定模型的極大極小問題變換為無約束可微優化問題，并通過BFGS（Broyden-Fletcher-Goldfarb-Shanno）算法快速求解出測點定位參數。

1 輪廓度模型的描述

國家標準GB/T 1182—2018《產品幾何技術規范（GPS）幾何公差形狀、方向、位置和跳動公差標注》指出，無基準要求的面輪廓度公差帶是包絡一系列圓球（諸球的直徑為公差T且球心位于理論曲面上）的兩包絡面之間區域，如圖1所示。面輪廓度評定過程就是不斷調整實際測點相對于理論曲面的空間位姿，保證誤差帶最小。

國家標準GB/T 1958—2017《產品幾何量技術規范（GPS）形狀和位置公差檢測規定》中，形狀誤差評定的最小區域準則為：被測要素的提取要素相對于理想要素的最大距離為最小。則輪廓度誤差的最小區域直徑為實際測點距離理想曲面最大值的2倍，數學上可定義為極小極大問題：

式中，n為測點數量；di（R，T）為實際測點到理論曲面的距離；R、T分別為測點集不斷調整位姿過程中所需要進行的旋轉變換矩陣和剛性平移矩陣；（α，β，γ）、（δx，δy，δz）分別為測點集在理論曲面坐標系中的旋轉量和平移量。

由式（1）可知，評定曲面輪廓度誤差是一個多元非線性的復雜尋優過程，需要解決兩個關鍵問題：計算測點到理論曲面的最小距離；求解測點集平移、旋轉的最優變換參數。

當曲面復雜的測點數量較多時，不可微函數的迭代計算量大，因此充分利用熵正則化解決大型數據集最優傳輸的優勢，結合BFGS算法設計了一種求解復雜曲面輪廓度的方法。首先利用分割逼近法確定測點到理論曲面的最小距離，通過熵正則化方法將評定模型中的極大極小問題轉化為含參數的無約束可微優化問題，然后利用BFGS算法快速求解出測點集的最優變換參數。具體的評定流程如圖2所示。

2 測點到曲面的最小距離

根據分割逼近方法［14］（圖3），計算測點pi（i為測點編號）到理論曲面S（u，v）的距離，基本步驟如下。

（1）將NUBRS曲面S（u，v）分別沿著u、v方向分割成（n+1）×（n+1）個曲面片，獲得網格點r（t）（ul，vk），其中，t為分割次數；l，k =0，1，…，n。

（2）計算某測點pi到網格點r（t）（ul，vk）之間的歐氏距離d（i，t）l，k。

（3）記錄測點pi到所有網格點距離最短的網格點r（t）min（ul，vk）及其距離d（t）min，則測點pi在曲面上對應的理論最近點q肯定在網格點r（t）min（ul，vk）鄰接的4個曲面片內。

（4）如果曲面片分割精度小于設定精度，則終止算法，獲取測點pi到曲面S（u，v）的最小距離d（t）min。否則，將網格點r（t）min（ul，vk）鄰接的4個曲面片進一步分割成（n+1）×（n+1）個曲面片，并令t←t+1得到新的網格點r（t）（ul，vk），轉至步驟（2）繼續執行。

3 無基準曲面輪廓度的評定

3.1 基于熵正則化的輪廓度模型轉換

最大熵原理［15］指出在滿足約束的條件下，熵值最大的概率分布是最符合客觀情況的一種無偏分布，從數學角度可定義為約束極值問題：

式中，H（η）為熵函數；η=（η1，η2，…，ηn）為隨機變量xi的概率分布；E（gj（xi））為可統計函數gj（xi）的均值。

在測點集不斷調整位姿以使誤差帶最小的過程中，測點集到理論曲面的最大距離問題可理解為一種不確定性的概率問題。為將不可微優化問題變換為可微優化問題，基于最大熵原理構建出光滑凝聚函數替代最大距離函數進行求解。

首先將輪廓度模型（式（1））變換為等價的約束非線性規劃問題：存在一個最小值Φ使得所有測點到理論曲面的距離都小于等于該值，即

其中，λi滿足單純形集合Λ={λi≥0|∑ni=1λi=1}。在符合給定的約束條件下，式（8）等價于距離最大值函數F（X）=maxdi（X）。

依據非負性和規范性的單純形集合，將式（8）中的λi理解為對應的距離函數di（X）等于最大值函數F（X）的概率，這樣L（X，λ）可視為原極大極小問題中距離函數di（X）的均值。依據最大熵原理，式（8）的極大值問題就是尋找一個滿足最大熵的概率分布函數λ（X）。可構建相應的熵函數：

首先輸入理論曲面和測點（仿真或實際），根據第2節的分割逼近方法求解測點到曲面的距離，然后采用不同的方法迭代求解測點的最佳定位參數，獲得曲面輪廓度，最后將其與蔡司三坐標儀器的實際測量結果進行對比以驗證方法的有效性。所有實驗數據均在CPU i5-4210M的個人計算機上進行，軟件平臺為MATLAB R2018a。

4.1 仿真實驗

在曲面上以Halton序列隨機生成400個理論測點。同時假定曲面在加工過程中的系統誤差ems=0.05（sinx+75120+siny－75120），隨機誤差emr符合正態分布N（0，0.012）；在測量過程中的系統誤差eis=（1，-1.5，0.8，0.1，-0.06，0.05），隨機誤差eir符合正態分布N（0，0.0052）。考慮上述模擬的加工誤差和測量誤差，將400個理論測點變換為仿真測點進行實驗。

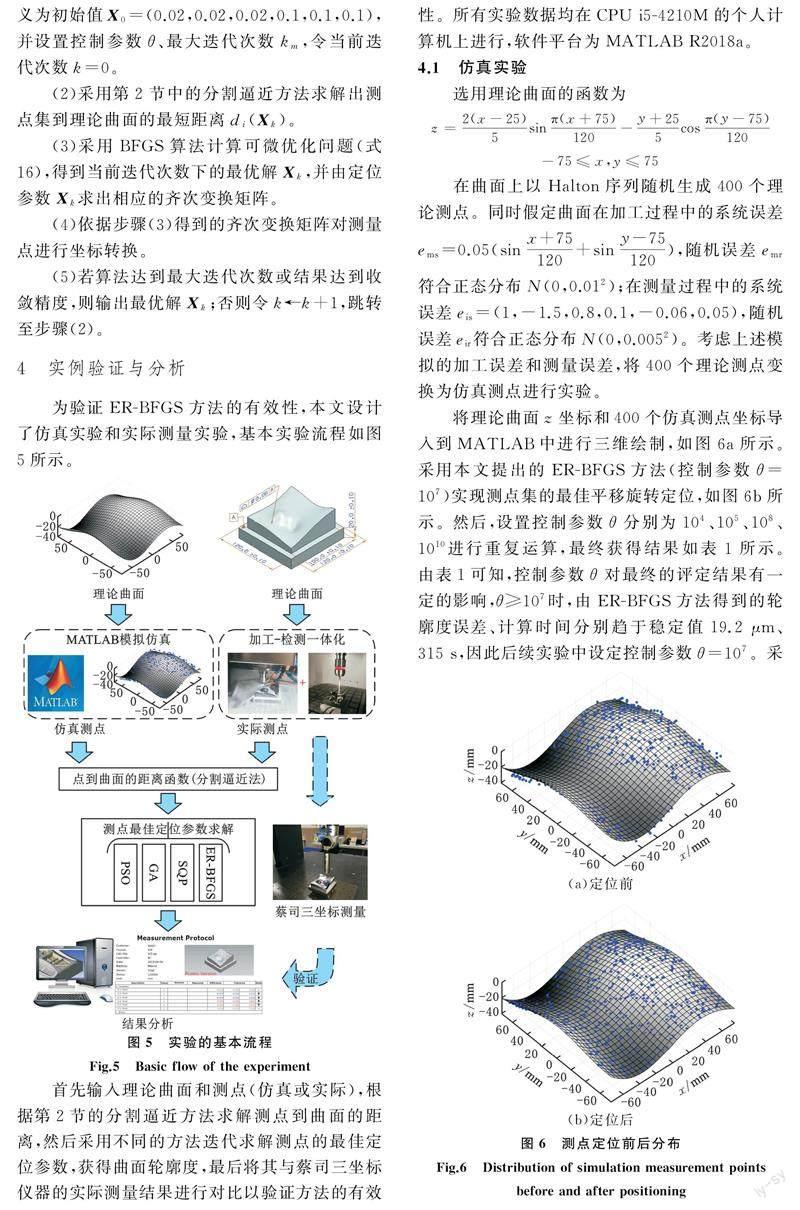
將理論曲面z坐標和400個仿真測點坐標導入到MATLAB中進行三維繪制，如圖6a所示。采用本文提出的ER-BFGS方法（控制參數θ=107）實現測點集的最佳平移旋轉定位，如圖6b所示。然后，設置控制參數θ分別為104、105、108、1010進行重復運算，最終獲得結果如表1所示。由表1可知，控制參數θ對最終的評定結果有一定的影響，θ≥107時，由ER-BFGS方法得到的輪廓度誤差、計算時間分別趨于穩定值19.2 μm、315 s，因此后續實驗中設定控制參數θ=107。采用PSO算法［17］、GA［14］、

SQP方法［5］以及ER-BFGS方法對曲面輪廓度進行評定，結果如表2所示。其中，各算法的最大迭代次數為500，終止收斂誤差為10-7。其他參數參照原文獻設置，GA的種群規模為50，交叉概率為0.8，變異概率為0.02；PSO的種群規模為30，學習因子c1=c2=2，慣性因子w=1。從表2中可以看出，PSO得到的輪廓度誤差精度最低，很可能陷入了局部最優；GA、SQP、ER-BFGS的輪廓度結果相近，但GA耗時最長，ER-BFGS在迭代次數與耗時方面要略優于SQP。

為探索本文方法在測點較多時的計算優勢，僅改變測點數量，按測點數400時的模擬方式生成仿真測點，并保證各方法參數、步驟一致，完成輪廓度評定。以Halton隨機分布方式，測點數量N分別取100、200、300、500、600，重復各上述方法的評定過程，客觀統計輪廓度結果和計算耗時如圖7所示。

由圖7可以看出，N為400，600時，PSO、GA的輪廓度精度分別19.4 μm、23.3 μm，與其他方法的輪廓度相差較大，說明沒能求解出最佳輪廓度，出現了局部最優問題。測點數量不同時，本文方法始終與SQP的輪廓度評定結果相近，基本能保證求解精度，但本文方法在計算耗時方面優于SQP，N為100、200、300、400、500、600的計算耗時相對于

SQP方法依次縮短了5.4%、8.2%、10.2%、14.9%、16.9%、19.5%。綜上所述，PSO、GA等群體智能算法的耗時普遍較長，且可能陷入局部最優，導致輪廓度精度較差；本文方法與SQP的計算結果相近，但在耗時方面略優于SQP，并且隨著測點的增多，計算效率的優勢更明顯。

4.2 在機測量實驗

為驗證本文方法在實際測量過程中的可行性，設計一個100 mm×100 mm的NUBRS曲面，以均勻分布方式規劃14×14個測點，如圖8所示。首先在MAKINO-V77三軸立式加工中心（重復定位精度為±1 μm）上對工件進行粗精加工，然后直接調用機床上的BLUM TC60測頭（德國波龍公司生產，重復精度為0.3 μm）。先對直徑29.9772 mm的標準球進行標定，通過標定值修正相應誤差以保證在機測量結果的有效性。最后，對該曲面按規劃好的采樣點進行在機測量，以獲取測點的實際坐標。同樣地，在蔡司CONTURA三坐標測量機（測量精度為1.7+L/350 μm）上以圖8所示的測點分布方式進行實際測量，并利用配套軟件Calypso計算其輪廓度。

將設計曲面和實際測點數據導入Geomagic Qualify軟件中，結果如圖9a所示，設置控制參數θ=107，采用ER-BFGS完成模型求解后，獲取重新定位的測點分布，如圖9b所示。同樣地，分別采用PSO、GA、SQP以及本文方法對該加工曲面進行輪廓度評定。Calypso測量軟件的計算結果如表3所示，各方法的迭代收斂情況如圖10所示。

由圖10、表3可以看出，在實際的在機測量實驗中，本文方法評定的輪廓度誤差為24.6 μm，與GA的24.9 μm、SQP的25.1 μm、PSO的24.4 μm大致相近，且與蔡司三坐標軟件實際測量結果24.2 μm相近，說明本文方法的在機測量數據是有效的。本文方法耗時為205 s，相比于PSO的479 s、GA的504 s、SQP的227 s分別縮短了57.2%、59.3%和8.5%。4種方法均能完成實際加工曲面的輪廓度評定，但本文方法在迭代次數和計算耗時方面均優于其他3種方法，說明在實際的在機測量環境下，本文方法在保證測量結果可信的前提下，確實能有效縮短測量過程占用機床的時間。

5 結語

復雜曲面的無基準輪廓度評定需要解決兩個關鍵問題，一是計算測點到理論曲面的最短距離，二是求解建立的最小區域評定模型。針對問題一，本文采用的分割逼近方法能有效求解點到曲面的距離。針對問題二，采用熵正則化原理和BFGS（ER-BFGS）算法相結合的方法求解曲面的定位參數，獲得曲面的輪廓度。實驗結果表明：基于最小區域準則的ER-BFGS方法能夠保證輪廓度評定結果的有效性，且計算效率高于SQP、GA等方法，測點較多時能有效縮短計算耗時，適用于復雜曲面的精密在機測量場景。

參考文獻：

［1］李文龍， 王剛， 田亞明， 等. 在機測量技術與工程應用研究進展［J］. 航空制造技術， 2022， 65（5）：14-35.

LI Wenlong， WANG Gang， TIAN Yaming， et al. Research Progress of On-machine Measurement Technology and Its Engineering Applications［J］. Aeronautical Manufacturing Technology， 2022， 65（5）：14-35.

［2］GAO W， HAITJEMA H， FANG F Z， et al. On-machine and In-process Surface Metrology for Precision Manufacturing［J］. CIRP Annals， 2019， 68（2）：843-866.

［3］宋紅滾， 劉國平， 劉建勝， 等. 基于點集拓撲學渦旋曲面輪廓度誤差評定［J］. 現代制造工程， 2017（12）：133-138.

SONG Honggun， LIU Guoping， LIU Jiansheng， et al. Evaluating of Surface Profile Error for Scroll Compressor Basedon Point Set Topology［J］. Modern Manufacturing Engineering， 2017（12）：133-138.

［4］王宇春， 孫和義， 唐文彥， 等. 最小條件下一般二次曲面輪廓度誤差的評定［J］. 儀器儀表學報， 2014， 35（8）：1803-1809.

WANG Yuchun， SUN Heyi， TANG Wenyan， et al. Evaluating General Quadric Profile Error Based on Least Condition Principle［J］. Chinese Journal of Scientific Instrument， 2014， 35（8）：1803-1809.

［5］LANG A， SONG Z， HE G， et al. Profile Error Evaluation of Free-form Surface Using Sequential Quadratic Programming Algorithm［J］. Precision Engineering， 2017， 47：344-352.

［6］ZHANG X， ZHANG H， HE X， et al. Fast Evaluation of Minimum Zone Form Errors of Freeform NURBS Surfaces［J］. Procedia CIRP， 2015， 27：23-28.

［7］LIU J. Calculation of Profile Error for Complex Surface［J］. Measurement， 2014， 48：183-186.

［8］ZHANG X， ZHANG H， HE X， et al. Chebyshev Fitting of Complex Surfaces for Precision Metrology［J］. Measurement， 2013， 46（9）：3720-3724.

［9］TAN G， ZHANG L， LIU S， et al. A Fast and Differentiated Localization Method for Complex Surfaces Inspection［J］. International Journal of Precision Engineering and Manufacturing， 2015， 16（13）：2631-2639.

［10］LU K， YU Y， PENG K， et al. Error Evaluation of Planar Curve Profile Based on an Improved Genetic Algorithm［C］∥2017 4th International Conference on Information Science and Control Engineering（ICISCE）. Changsha， 2017：312-316.

［11］萬潤， 王琳， 盛步云. 基于改進粒子群算法的自由曲面輪廓度評定［J］. 組合機床與自動化加工技術， 2021（10）：10-13.

WAN Run， WANG Lin， SHENG Buyun. Freeform Surface Profile Evaluation Based on Improved Particle Swarm Optimization Algorithm［J］. Modular Machine Tool & Automatic Manufacturing Technique， 2021（10）：10-13.

［12］HUANG Z， WEI P， LI C， et al. Aero-engine Blade Profile Reconstruction Based on Adaptive Step Size Bat Algorithm and Visualization of Machining Error［J］. Proceedings of the Institution of Mechanical Engineers， Part C：Journal of Mechanical Engineering Science， 2020， 234（1）：49-65.

［13］HE G， ZHANG M， SONG Z. Error Evaluation of Free-form Surface Based on Distance Function of Measured Point to Surface［J］. Computer-Aided Design， 2015， 65：11-17.

［14］廖平. 基于遺傳算法和分割逼近法精確計算復雜曲面輪廓度誤差［J］. 機械工程學報， 2010， 46（10）：1-7.

LIAO Ping. Calculating of Complex Surface Profile Error Based on Subdivision Approach Algorithm and Genetic Algorithm［J］. Journal of Mechanical Engineering， 2010， 46（10）：1-7.

［15］方興華， 宋明順， 魯偉. 測量不確定度信息約束下的最大熵分布研究［J］. 系統科學與數學， 2017， 37（12）：2337-2346.

FANG Xinghua， SONG Mingshun， LU Wei. Research on Maximum Entropy Distribution under Measurement Uncertainty Constraints［J］. Journal of Systems Science and Mathematical Sciences， 2017， 37（12）：2337-2346.

［16］袁志聰， 魯鐵定， 劉瑞. 一種基于BFGS修正的正態分布變換點云配準方法［J］. 測繪通報， 2020（10）：38-42.

YUAN Zhicong， LU Tieding， LIU Rui. A Normal Distribution Transform Point Cloud Registration Method Based on BFGS Correction［J］. Bulletin of Surveying and Mapping， 2020（10）：38-42.

［17］廖平. 基于粒子群算法和分割逼近法的復雜曲面輪廓度誤差計算［J］. 中國機械工程， 2010， 21（2）：201-205.

LIAO Ping. Calculation of Complex Surface Profile Errors Based on Hybrid Particle Swarm Optimization Algorithm［J］. China Mechanical Engineering， 2010， 21（2）：201-205.

（編輯 張 洋）

作者簡介：

付高財， 男， 1989年生， 實驗員。研究方向為精密測量、數字制造。發表論文10余篇。E-mail：whutjdfgc@163. com。

盛步云（通信作者）， 男， 1964年生， 教授、博士研究生導師。研究方向為數字集成制造、智能工廠。發表論文120余篇。E-mail：shengby@whut. edu. cn。

收稿日期：2022-05-05

基金項目：湖北省科技重大項目（2021AAA007）