煤礦設備運行狀態在AGB組合模型下的預測分析研究

李 杰

(山西焦煤集團 霍州煤電集團呂臨能化有限公司, 山西 臨縣 033200)

目前,呂臨能化有限公司機電設備復雜性提高,使用單一預測模型進行設備運行狀態評估出現精度低以及適用范圍小等的問題,造成設備維護不到位,影響設備的安全運行。基于此,提出將Arima模型、BP神經網絡與GM(1,1)模型相結合,通過權重分配設計一個全新的運行狀態預測模型,實現煤礦設備運行狀態的精確預測評估,保證設備的安全運行。煤礦設備多且復雜程度較高,為方便研究,選用該礦工作面使用的MG200500-AWD型采煤機為代表展開分析。

1 采煤機狀態評價與描述

將傳感器安裝在采煤機的關鍵部位來完成重點參數的采集與監控,通過對設備使用過程中數據的波動情況對比,進行設備運行狀態的預測評估。圖1為采煤機健康狀態評價圖。

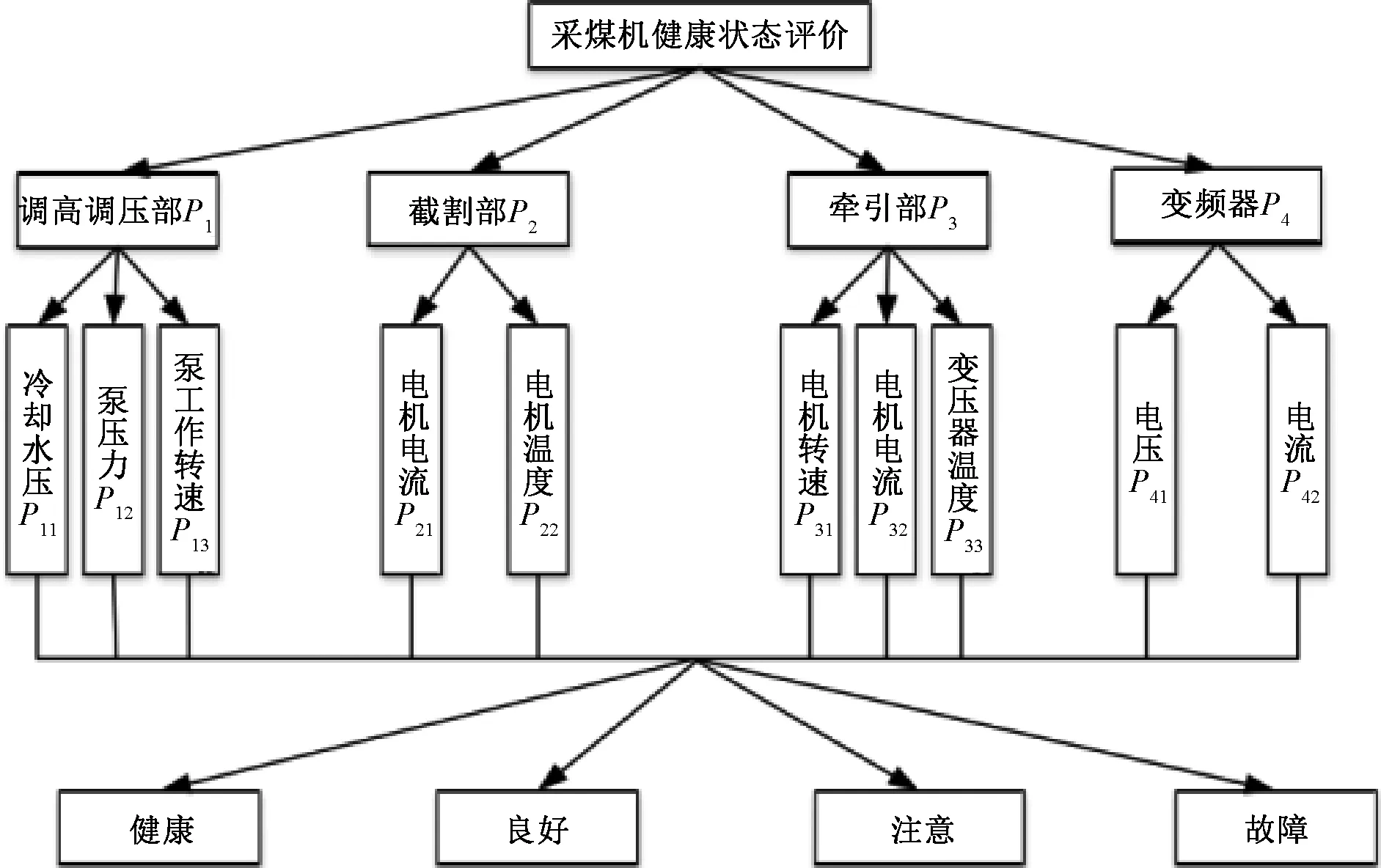
圖1 采煤機健康狀態評價圖

根據圖1,可以將采煤機分為多個關鍵部件,此時采煤機的運行狀態便能夠用集合來表示,即P=[P1,P2,…,Pi,…,Pm],而采煤機第i個部件狀態也可以用集合來表示,即Pi=[Pi1,Pi2,…,Pii,…,Pim]. 通過資料分析,將采煤機健康狀態評價指標進行匯總,具體見表1.

表1 采煤機健康狀態評價指標表

基于表1,按照參數極限值完成采煤機健康狀態等級劃分,設備不同的狀態等級對應的劣化度指數范圍見表2.

表2 采煤機健康狀態等級表

2 基于AGB組合模型的煤礦設備運行狀態預測模型定義與建模

2.1 ARIMA模型定義

ARIMA模型的預測原理是根據時間變化將預測數據對象形成的時間序列作為隨機序列,根據對應的數學模型描述此時間序列,根據輸入已知確定參數來預測模型的未知數值,從而得到完整數學模型,可以實現預測未來參數的作用。ARIMA模型,其完整表達為差分自回歸移動平均模型[1]. ARIMA模型由3種模型組成,即自回歸模型、移動平均模型、自回歸移動平均模型。在應用ARIMA模型過程中,要重視觀察數據的穩定性,當出現不符合要求的數據時,應當先對其進行差分運算,隨后把運算后的新數據代入到ARMA模型中,確定模型的相關性系數,自相關函數表示在不同時間內相同序列的相關程度,而偏自相關函數則表示排除干擾變量外其他兩個變量的相關程度,隨后通過自相關圖完成對比,最終得出最佳系數,具體的控制流程圖見圖2.

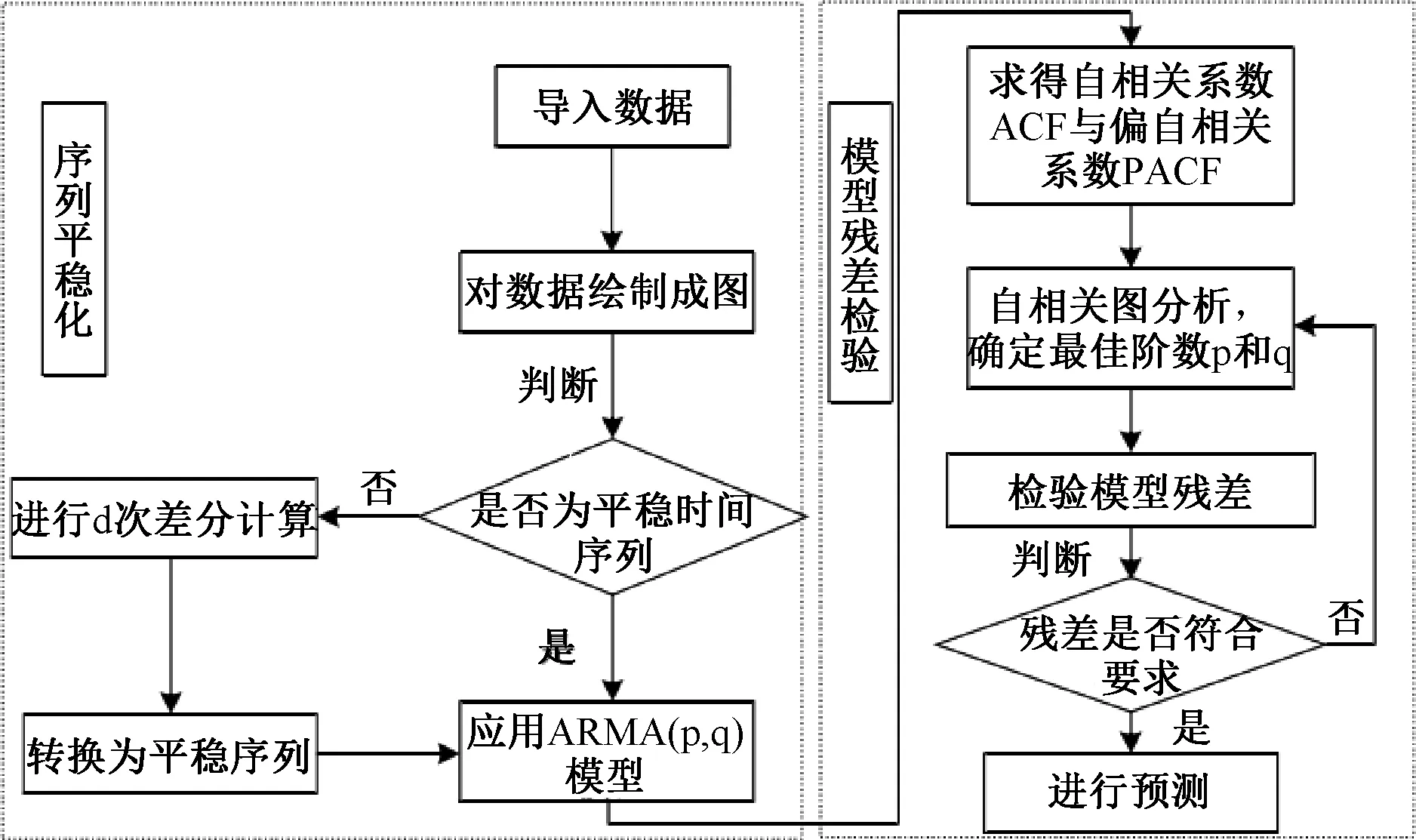
圖2 ARIMA模型控制流程圖

2.2 GM(1,1)模型定義

GM(1,1)模型即灰色模型,其預測原理是以一階微分方程為基礎的模型方法,因此在GM(1,1)模型搭建時,應該先確定原始數列。

假設原始數列為式(1):

x(0)={x(0)(1),x(0)(2),x(0)(3),…,x(0)(m)}

(1)

式中:x(0)包含m個元素,x(1)作為x(0)的累加生成序列,其計算方法見式(2):

x(1)={x(1)(1),x(1)(2),x(1)(3),…,x(1)(m)}

(2)

x(1)數列的均值數列用v(0)來表示,其計算方式見(3):

v(0)={z(1)(2),z(1)(3),z(1)(4),…,z(1)(m)}

(3)

v(0)(k)=0.5x(1)(k)+0.5x(1)(k-1)

(4)

(5)

由(2)、(3)計算可得,GM(1,1)模型的灰微分方程:

d(k)+av(0)(k)=b

(6)

模型確定好后,對模型的合理性進行檢驗,精度檢驗通常采用的方法有相對誤差檢驗、關聯度檢驗以及后驗差檢驗,后驗差檢驗使用范圍較廣。

后驗差計算公式為:C=S2/S1,其中S1為原始數列的方差,S2為殘差的方差,其比值C值越小說明數據的離散程度越高,說明GM(1,1)模型精度等級越高。

2.3 BP神經網絡模型定義

BP神經網絡又稱為誤差逆傳播算法,其預測的原理即為,將輸出的誤差作為預測的輸入值,預測輸出上一層的運算誤差,通過往復計算,獲取全部層的誤差預測。圖3為BP網絡拓撲結構圖。根據圖3,在預測過程中,需要把誤差反向傳給隱含層中的神經元,改變隱含層到輸出層的比重以及輸出層對應的閾值[2-3].

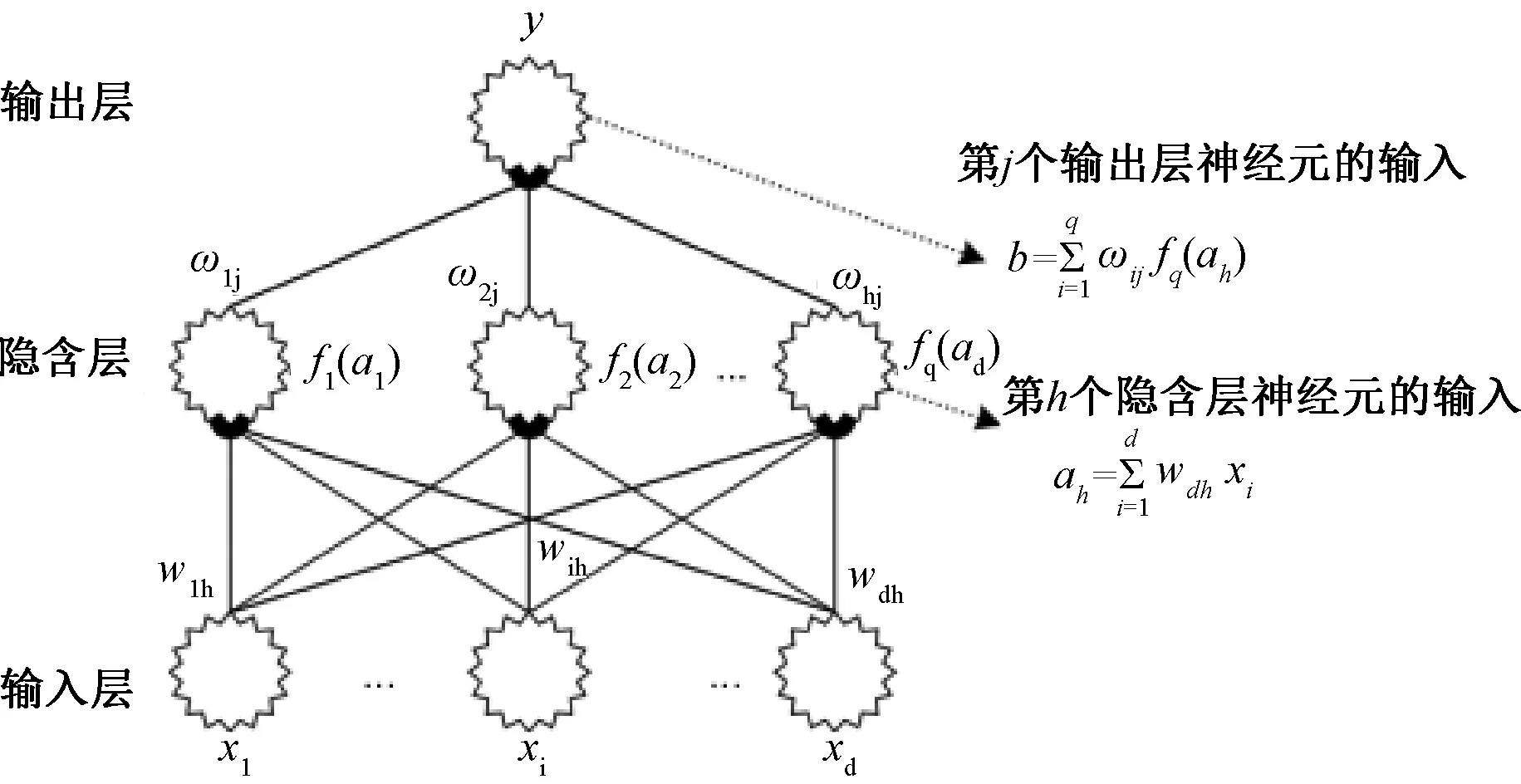
圖3 BP網絡拓撲結構圖

BP神經網絡預測訓練主要分為訓練樣本和反向預測兩大部分。根據輸出的真實數據信息與期望數據進行比對,將兩者之間的差異代入到隱含層中的神經元,通過調整網絡參數降低兩者差異,直到滿足要求后停止。反向預測過程見圖4.

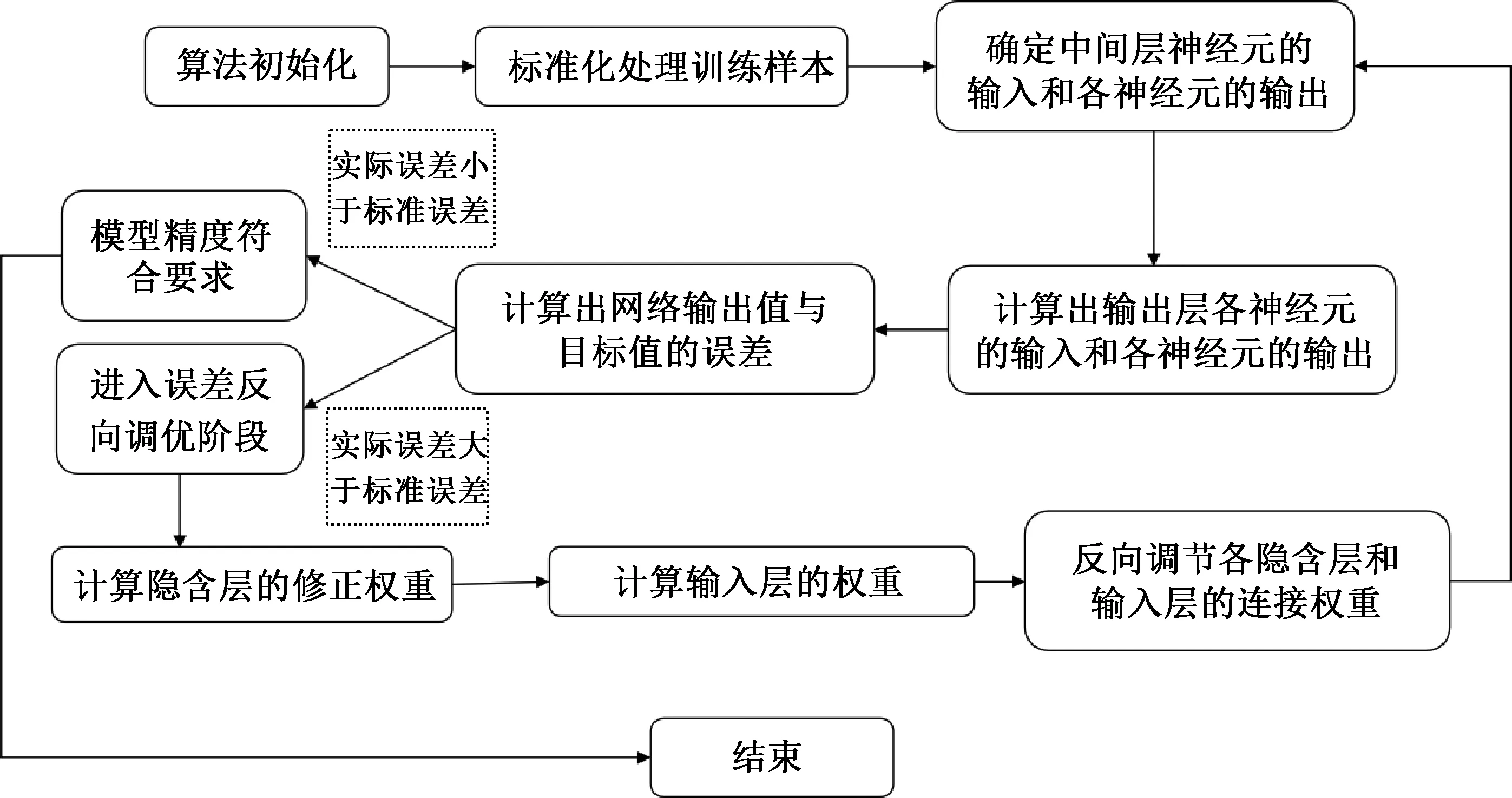
圖4 BP神經網絡預測流程圖

2.4 AGB組合預測模型定義與建模

在采用單一模型預測時,其結果經常會偏離實際,基于此,提出了AGB組合預測模型,即ARIMA模型、GM(1,1)模型與BP神經網絡模型相結合的方式,實現煤礦機電設備運行狀態的預測。在組合模型作用過程中能夠將各組成單個模型的優點進行集中,有效提高預測的準確性。3種模型的權重計算選擇預測精度較高的方差-協方差權重法進行。

設ARIMA模型預測值為z1,預測誤差e1,加權系數w1;GM(1,1)模型預測值為z2,預測誤差e2,加權系數w2;BP神經網絡模型預測值為z3,預測誤差e3,加權系數w3;AGB模型預測值為za,預測誤差ea. 故AGB組合模型預測值:

za=z1w1+z2w2+z3w3

(7)

AGB組合模型預測誤差方差值:

3w1w2w3cov(e1,e2,e3)

(8)

式中,w1,w2,w3計算如下:

(9)

(10)

(11)

在上述公式中,組合模型的預測誤差方差值Var(ea)的最小值分別小于Var(e1)、Var(e2)、Var(e3),反映出AGB組合預測模型準確度比單個模型預測準確度都高。按照上述的AGB組合模型理論計算過程,繪制組合模型流程結構圖,見圖5.

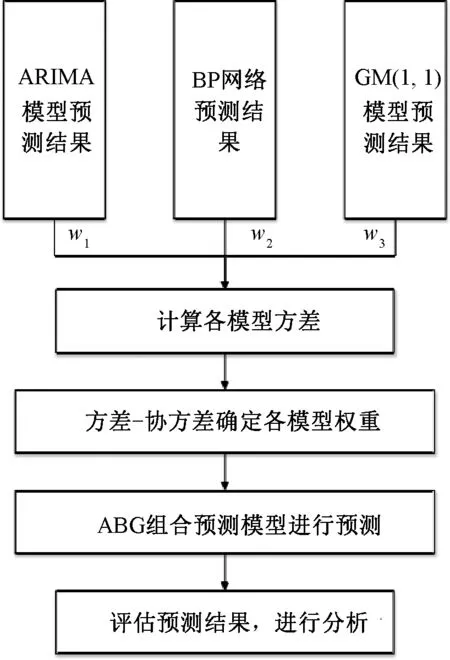
圖5 AGB組合模型流程結構圖

在使用AGB組合模型進行故障預測時,一般分為5個步驟[4].

1) 將A、G、B 3個模型得出的預測結果匯總導入。2) 分別計算3個模型的方差。3) 根據方差-協方差權重法計算出3個模型的權重。4) 將數據導入模型進行預測,得出預測數列。5) 進行預測結果的評價,并展開分析。

3 基于AGB組合預測模型的采煤機運行狀態預測模型實驗驗證

以呂臨能化有限公司采煤工作面采煤機為研究對象,使用調高調壓部傳感器,采集泵冷卻水壓數據對AGB組合預測模型與單個預測模型的預測精度進行對比測試[5]. 將采集水壓數據按照每秒采集一次的規律進行提取,再將其分別導入ARIMA模型、GM(1,1)模型、BP神經網絡模型,計算單個模型的方差,再根據式(9)(10)(11)計算對應模型的權重比,將對應數據導入AGB組合模型完成預測,對比結果見表3,計算的方差值Var(e1)=0.05,Var(e2)=0.08,Var(e3)=0.07,權重比w1=0.26,w2=0.39,w3=0.35.

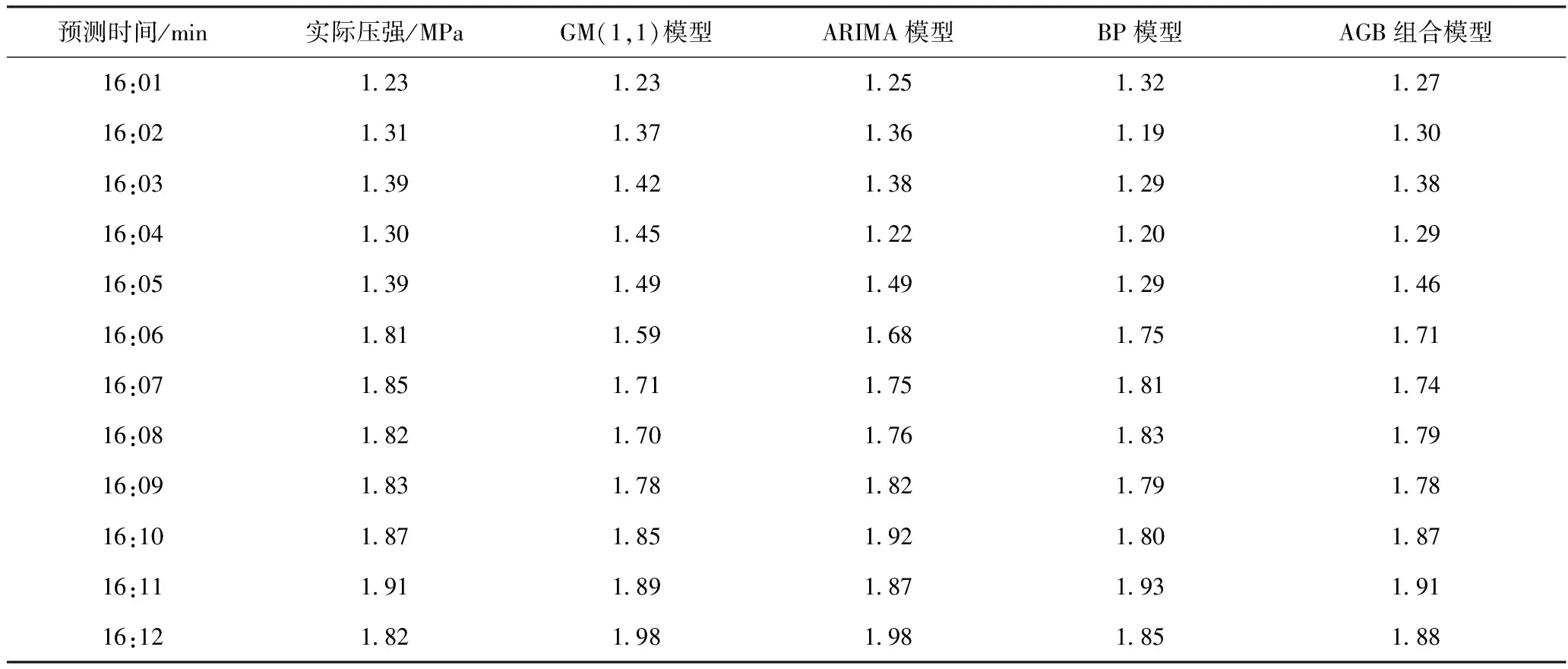
表3 采煤機調高調壓部泵冷卻水壓對應各模型的預測結果表

根據表3,實際數據、單一模型與組合模型預測結果,繪制圖6(a)預測結果對比圖,從圖中可以看出,使用AGB組合模型預測結果與原始數據相比一致性更好。基于此,對各預測模型的殘差分布進行求解,通過對比,確認組合模型與單一模型的預測精度差異,其殘差對比見圖6(b).

根據圖6(b)可知,ARIMA模型殘差平均值0.058,GM(1,1)模型殘差平均值0.09,BP神經網絡模型殘差值0.062,AGB組合模型殘差值0.02,說明AGB組合模型的預測精度相較單一模型最高,準確性最好,后續在進行煤礦設備運行狀態預測時建議使用AGB組合模型。

4 結 語

隨著煤炭行業自動化技術的不斷深入,實現少人化、無人化工作面已經成為煤炭人的奮斗目標。為解決王坪煤業有限公司采煤工作面煤礦設備運行狀態評估時存在的預測精度低、單一模型適用范圍小等問題,將Arima模型、BP神經網絡以及GM(1,1)模型相結合,通過構建采煤機運行狀態預測模型以及實驗驗證分析,實現了預測精度更高的采煤機運行狀態預測分析,按照預測結果現場人員能夠及時對煤礦機電設備進行干預,保證井下設備的安全運行,為井下生產提供保障。