非飽和花崗巖殘積土的彈塑性本構模型與驗證

張 強,劉一奧

(1.中國海洋大學 環境科學與工程學院,山東 青島 266000;2.山東省魯南地質工程勘察院,山東 濟寧 272100;3.吉林大學 建設工程學院,長春 130026;4.國家開發銀行吉林省分行,長春 130022)

非飽和花崗巖殘積土是一種特殊的物質材料[1-3],具有復雜的物理力學特性.由于母巖巖脈分布不均且抗風化能力不同,導致風化的殘積土在力學性質上表現出不均勻性和各向異性,其“兩頭大、中間細”的顆粒級配特點,使花崗巖殘積土表現為結構松散和透水性強.水分進入土后會溶解其中包裹粗顆粒土骨架的可溶鹽,導致土骨架損傷,進而發生崩解現象.自然界中花崗巖殘積土大多呈非飽和狀態,非飽和與飽和條件下土的性質具有顯著差異,工程性狀也更復雜.針對上述問題,在了解殘積土的特殊物質組成、物理和力學特性基礎上,需構建合理的描述方法以提高土體變形預測的可靠性.目前通常以飽和土的理論依據解決非飽和土的工程問題,這種假設導致計算結果與實際工程差距較大.近年來,研究人員對土的非飽和力學特性的測試和描述理論進行了探索并取得較大進展,提出了更合理的非飽和土的彈塑性模型,如文獻[4]以吸力和凈應力為雙應力變量提出了BBM(Barcelona basic model)模型,采用LC(loading-collapse)屈服線表達吸力對屈服應力的硬化規律;文獻[5-7]以BBM模型為基礎,提出了考慮吸力為附加應力狀態變量的非飽和土本構模型.這類模型忽視了土體飽和度和孔隙率變化對土體性質的改變.在流-固模型中,對土中水分變化的表述一般采用土-水特征曲線模型,如Brooks-Corey模型、Van Genuchten模型和Fredlund-Xing模型[8-11],這些模型可間接預測非飽和土體的滲流、強度和變形等性質.Wheeler等[12]以飽和度為模型參數,采用雙變量理論建立了水-力全耦合模型(GCM);熊勇林等[13]基于水-土-氣三相耦合模型分析了非飽和邊坡穩定性.在非飽和土的本構模型和應用研究中,由于考慮了基質吸力和飽和度對模型性質的影響,因此有些模型的數學形式較復雜.基于此,本文結合花崗巖殘積土的非飽和力學特性,基于修正的劍橋模型,通過調整屈服面形態,將飽和度作為參數量,推導修正劍橋模型的基本增量格式,實現非飽和土的變形分析.

1 考慮非飽和特性的修正劍橋模型

在飽和土修正劍橋模型的基礎上提出非飽和土的修正劍橋模型,主要考慮飽和度影響的屈服面擴展形狀,非飽和土的修正劍橋模型屈服面示意圖如圖1所示.

圖1 非飽和土的修正劍橋模型屈服面示意圖Fig.1 Schematic diagram of yield surface of modified Cambridge model for unsaturated soils

1.1 屈服面方程

非飽和土由固體顆粒及充填在顆粒間孔隙中的水和氣組成,用有效應力表示應力分量為

(1)

若將χ簡化為飽和度Sr,則式(1)可變為

p′=(p-ua)+Sr(ua-uw),

(2)

由式(2)可知,若忽略孔隙中氣壓的影響,則非飽和土體的有效應力與孔隙水壓力和土體的飽和度均相關,其力學特性在一定程度上受土-水特征曲線影響.

在p-q平面上建立屈服軌跡方程為

(3)

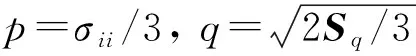
與修正劍橋模型相比,考慮了土體的抗拉屈服強度pt,并考慮了應變強化與飽和度強化.式(3)與修正劍橋模型保持相同的形式.屈服面軌跡F的大小可用pc函數表示.在p-q平面內屈服面為橢圓形(圖1),此外,圖1中還有一個與飽和度Sr有關聯的LC屈服面,為在Sr-p′平面上橢圓屈服軌跡F的交線,反映了在飽和度變化下屈服面不斷強化的過程[14-16].

1.2 流動法則

為簡單,采用相關聯的流動法則.當屈服面臨界狀態小于應力狀態時,可將塑性勢函數對應為屈服面方程,此時應變(塑性)的流動方向為垂直于屈服面并指向內部.在此將塑性應變增量視為塑性剪應變與體應變增量之和[17].根據傳統塑性位勢理論,塑性體應變與剪應變增量的形式為

(4)

當采用相關聯的流動法則時,屈服面方程F與塑性勢函數Q一致.引入變量剪脹比Ds用以描述各應變分量間的函數關系,Ds可表示為

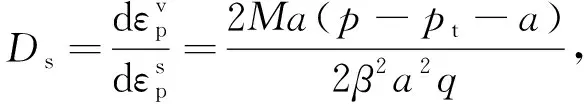
(5)

結合式(4)和式(5)可得塑性總應變增量用塑性剪應變增量的表達式為

(6)

其中σij為應力張量,A,B,C均為列向量.

對于強化準則[18],定義為

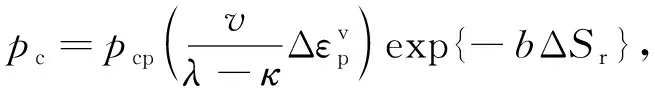
(7)

其中b為(-Sr)-lnpc直線的斜率,κ和λ分別為超固結和正常固結線的斜率,pcp為先期固結壓力.

2 增量型本構關系推導

增量型模型一定程度上可避免因應力-應變關系的非線性所導致的收斂問題,適于用戶利用商業軟件的用戶接口實現數值計算.考慮彈塑性材料的基本特點,則有

{Δσ}=(De){Δεe}=(De){Δε-Δεp},

(8)

其中{Δσ}為應力增量,{Δεe}為彈性應變增量,{Δε}為總應變增量,{Δε}={Δεe}+{Δεp},(De)為彈性剛度矩陣.

根據一致性條件,屈服面方程滿足等量關系

(9)

由偏應力項、體應力項和總應力項間的關系可得式(9)中偏應力項為

(10)

由式(9)和式(10)可得

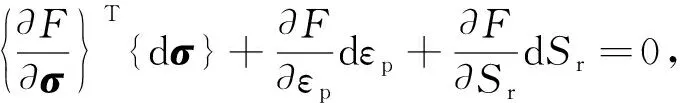
(11)

將式(8)代入式(11)可得

(12)

將dεp項合并,并將其系數消去可得

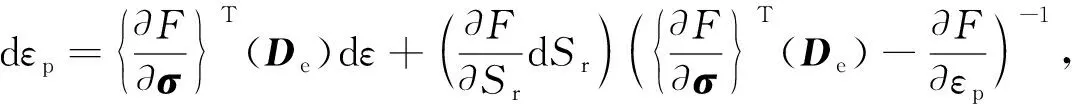
(13)

將式(13)代入式(8)并合并同類項可得

{Δσ}=(De){Δε-Δεp}=(Dep){dε}+(DSr){dSr}.

(14)

由此得到應力-應變Jacobi矩陣和飽和度-應力Jacobi矩陣分別為

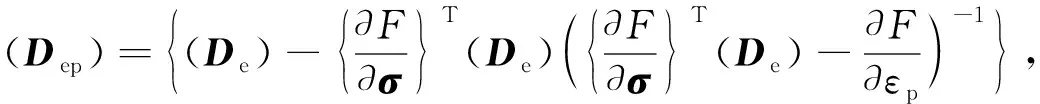
(15)

(16)

考慮應變-飽和度耦合的計算格式,需將上述Jacobi矩陣進行擴展,得到修正劍橋模型的增量型本構關系為

{dσ}=(Dw){dεw},

(17)

由于(Dw)矩陣中以飽和度Sr為變量,通過間接表達基質吸力對力學性質的影響,因此求解較簡單.

3 模型驗證

為驗證模型的可靠性,采用FORTRAN編程語言形成用戶自定義材料力學行為(UMAT)子程序,利用ABAQUS/STANDARD求解器進行非飽和土的應力與變形分析,模型參數和取值列于表1.先在ABAQUS CAE(前處理工具)內輸入材料參數,再利用CAE內置功能生成inp文件提供給ABAQUS/STANDARD求解器,由inp文件內部的聲明命令求解器調用UMAT子程序,讀取材料參數并進行應力變形分析.為驗證模型的有效性,采用室內非飽和三軸實驗結果進行對比.

表1 模型參數和取值

圖2 樣品的粒徑分布曲線Fig.2 Particle size distribution curve of sample

以直徑50 mm和高度100 mm的圓柱體花崗巖殘積土為樣品,在GDS(global digital system)非飽和三軸儀上開展三軸剪切實驗.樣品的粒徑分布曲線如圖2所示,根據《土的工程分類標準》(GB/T50145-2007)[19],樣品中礫砂、砂粒和細粒粒組的相對質量百分數分別為16%,51%和33%,不均勻系數Cu=100,曲率系數Cc=0.73.在應力150 kPa和基質吸力分別為25,75,150 kPa下進行實驗.在實驗開始前,先通過抽氣法使樣品飽和,再通過GDS非飽和測試系統給樣品施加5 kPa的基質吸力使土樣進一步飽和,使其飽和度大于95%.GDS三軸實驗分為吸力平衡、等吸力固結和等吸力剪切破壞3個階段.在吸力平衡階段利用軸平移技術,使孔隙氣壓力保持不變而改變孔隙水壓力,以此實現基質吸力平衡.若反壓體積變化量在連續24 h內不超過50 mm3,則認為達到基質吸力平衡.在等吸力固結階段,凈圍壓取150 kPa,固結時需確保吸力保持不變.在等吸力剪切破壞階段,控制剪切速率0.05 mm/min,軸向應變以15%為破壞標準.

由測試得到的土-水特征曲線確定花崗巖殘積土體積含水率θw和基質吸力ψ的關系為

(18)

采用上述模型計算時,考慮與三軸剪切實驗條件相同,施加預定義孔壓場,其大小為150 kPa,同時預設0.9的初始孔隙率.給樣品表面施加不排水邊界條件,以控制加載過程中基質吸力.

在150 kPa凈圍壓,基質吸力分別為25,75,150 kPa下的數值模擬與室內實驗數據的對比結果如圖3所示.由圖3可見,無論是偏應力-軸向應變關系,還是體應變-軸向應變關系,在3種基質吸力下,當軸向應變小于6%時,預測結果與實驗值有一定的差距,當軸向應變大于6%時,具有良好的一致性.所建模型在模擬非飽和土的剪縮性能上具有良好的表現.

圖3 不同基質吸力下模型計算結果與實驗數據比較Fig.3 Comparison between model calculation results and test data under different matrix suction

綜上所述,本文在非飽和修正劍橋模型的基礎上,對模型的屈服面性狀進行了修正,并將飽和度作為參數,推導了修正劍橋模型的增量型本構關系.模型參數少,物理意義明確,模型計算結果與花崗巖殘積土的非飽和三軸實驗結果一致,表明所建模型具有較好的可靠性.