Fisher信息在噪聲估計精度分析中的應用

潘銘櫻,馮象初

(西安電子科技大學 數學與統計學院,西安 710126)

圖像在人類生活中具有重要作用[1],人們所接收到的信息大部分通過圖像傳遞[2].但在圖像被操作過程中會產生許多無用的信息,干擾了人們對圖像信息的理解以及后續的處理結果[3],因此在圖像進行處理前必須予以糾正,使得圖像去噪研究備受關注.除基于濾波[4]、基于偏微分方程[5]和基于非局部自相似[6]等的傳統圖像算法外,新興的基于深度學習的方法[7-8]也成為目前研究的重點.但這些算法大多數要求圖像的噪聲參數已知,而這在實際生活中不現實,因此噪聲估計成為圖像去噪過程中的重要一環.噪聲估計的方法有很多[9-21],其中基于極大似然方程估計圖像噪聲參數是一個重要的研究方向[17-21].文獻[19]研究表明,平坦圖像塊的信息主要來自于噪聲,所以其通過極大似然估計從紋理較少的圖像塊中估計噪聲參數,該算法取得了較好的效果.

分析估計參數的精度可以更清楚地了解參數與真實數據的匹配程度,減小因參數誤差對實驗結果造成的不良影響.雖然相關噪聲估計的研究目前較多,但針對得到參數精度的研究卻相對較少.Fisher信息[22]是數理統計中的重要概念,可用于觀測可觀察隨機變量攜帶的關于其概率與所依賴的未知參數的信息量.本文以文獻[19]中的方法為例,利用Fisher信息分析估計參數的精度.

1 預備知識

1.1 Fisher信息相關定理及推論

定義1(Fisher信息)[23]設X=(X1,X2,…,Xn)T～f(x,θ),θ∈Θ?p為C-R(Cramer-Rao)分布族.設X1,X2,…,Xn為獨立同分布樣本,X1～f(x1,θ),l(θ,x1)=logf(x1,θ),則有

引用大數定律和中心極限定理,則有

其中I(θ)即為X的Fisher信息.

定理1(強相合性)[23]設X=(X1,X2,…,Xn)T～f(x,θ),θ∈Θ?p為C-R分布族,并設X1,X2,…,Xn獨立同分布,Θ為p上的開集.則似然方程在n→+∞時必有解并且是強相合的.即對真參數θ0∈Θ,有

定理2(漸近正態性)[23]設X=(X1,X2,…,Xn)T～f(x,θ),θ∈Θ?p為C-R分布族,并設X1,X2,…,Xn獨立同分布,Θ為p上的開集.假設似然方程在n→+∞時有相合解且假設L(3)(θ)在Θ中存在并連續,則為θ的最優漸近正態估計,且有

1.2 噪聲估計

文獻[19]提出了一種針對通用信號相關噪聲模型的參數估計方法,該模型通過改變參數值可以表示不同類型的噪聲.該觀測到的噪聲模型可表示為

x=s+k0δ0+k1sγ·δ1,

(1)

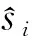
其中M是選取的弱紋理塊數量.對應的能量泛函為

(2)

2 噪聲估計的精度分析

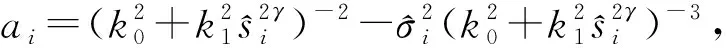
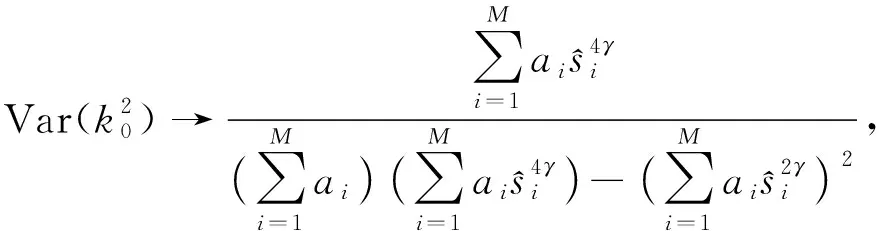
(3)

(4)

所以其Hessian矩陣為

從而可計算樣本的Fisher信息為

然后對矩陣I(k)求逆,得

當n→∞時,有式(3)和式(4).證畢.

目前流行的圖像處理軟件,通常用8位表示一個像素,這樣灰度級分為256等,像素位于0～255內,每個等級代表不同的亮度,稱為圖像的標準表示.為便于表示,還可對圖像像素進行歸一化處理,此時圖像的像素則位于0～1內.本文以這兩種圖像為例,分別分析用不同像素表示對噪聲估計結果的影響.

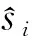
3 數值實驗與分析

為驗證理論推導結果即定理3的準確性,本文進行兩組實驗: 第一組實驗是直接對不同模式下圖像噪聲參數進行估計,分析兩個參數出現的誤差范圍;第二組實驗是通過噪聲估計算法以及改進的圖像去噪算法進行盲去噪,以分析在不同圖像模式和不同噪聲占比下圖像的去噪結果.實驗中采用的圖像都是標準測試集中的圖像,如圖1所示.

圖1 標準測試集圖像Fig.1 Images of standard test set

3.1 參數精度驗證

根據定理3可推出在不同的圖像表示模式下圖像兩種噪聲的參數精度相反.本文用不同的圖像模式分別表示標準測試集中的圖像,并添加不同參數的噪聲,用基于極大似然的噪聲估計算法對噪聲進行估計.在該過程中令指數參數γ恒等于常數.

對標準像素下的圖像,首先在k1值恒定的情況下計算k0在不同值下的估計值,并將多張圖像的估計數據進行整合,得到參數k0的誤差區間;然后固定k0,用相同方法分析k1的誤差區間.本文將誤差結果用棒形圖表示,如圖2所示.由圖2可見,用標準像素表示圖像時,極大似然估計得到的加性噪聲參數k0的誤差大于乘性噪聲參數k1的誤差.

為保證歸一化后的圖像在加入噪聲后的噪聲程度不發生改變,本文將上述實驗中設置的加性噪聲的參數與255的比值作為加性噪聲參數加入圖像進行實驗.乘性噪聲與圖像的像素值相關,在圖像歸一化后相當于加入的乘性噪聲已經進行了歸一化處理,所以k1值不發生變化.同理,在一個參數固定的情況下利用多張圖像的估計結果分析另一個參數的誤差區間,當圖像像素值位于0～1內時參數k0和k1的誤差棒形圖如圖3所示.由圖3可見,此時k0的噪聲估計誤差非常小,而k1的誤差相對大很多.

上述實驗結果與經過理論分析得到的定理3相符,表明本文的理論分析正確.

3.2 算法盲去噪驗證

文獻[6]提出了一個可行的去除信號相關噪聲的全局最小二乘(total least square,TLS)算法,本文對其進行適當改進,得到針對廣義混合噪聲模型的去噪算法,并用其測試當模型中的加性噪聲和乘性噪聲分別處于主要地位時,不同表示類型圖像的去噪結果,以驗證定理3的正確性.為便于研究,本文設指數參數γ=1.

圖2 標準圖像噪聲參數估計結果Fig.2 Estimation results of standardimage noise parameters

圖3 歸一化圖像噪聲參數估計結果Fig.3 Estimation results of normalizedimage noise parameters

首先是乘性噪聲占比較大的實驗設定,在這組實驗中設(k0,k1)=(5,0.3),(k0,k1)=(5,0.5),此時加性噪聲程度相對較小而乘性噪聲相對較大.得到圖像的峰值信噪比(peak signal-to-noise ratio,PSNR)值以及結構相似度(structural similarity index measure,SSIM)值分別列于表1和表2.

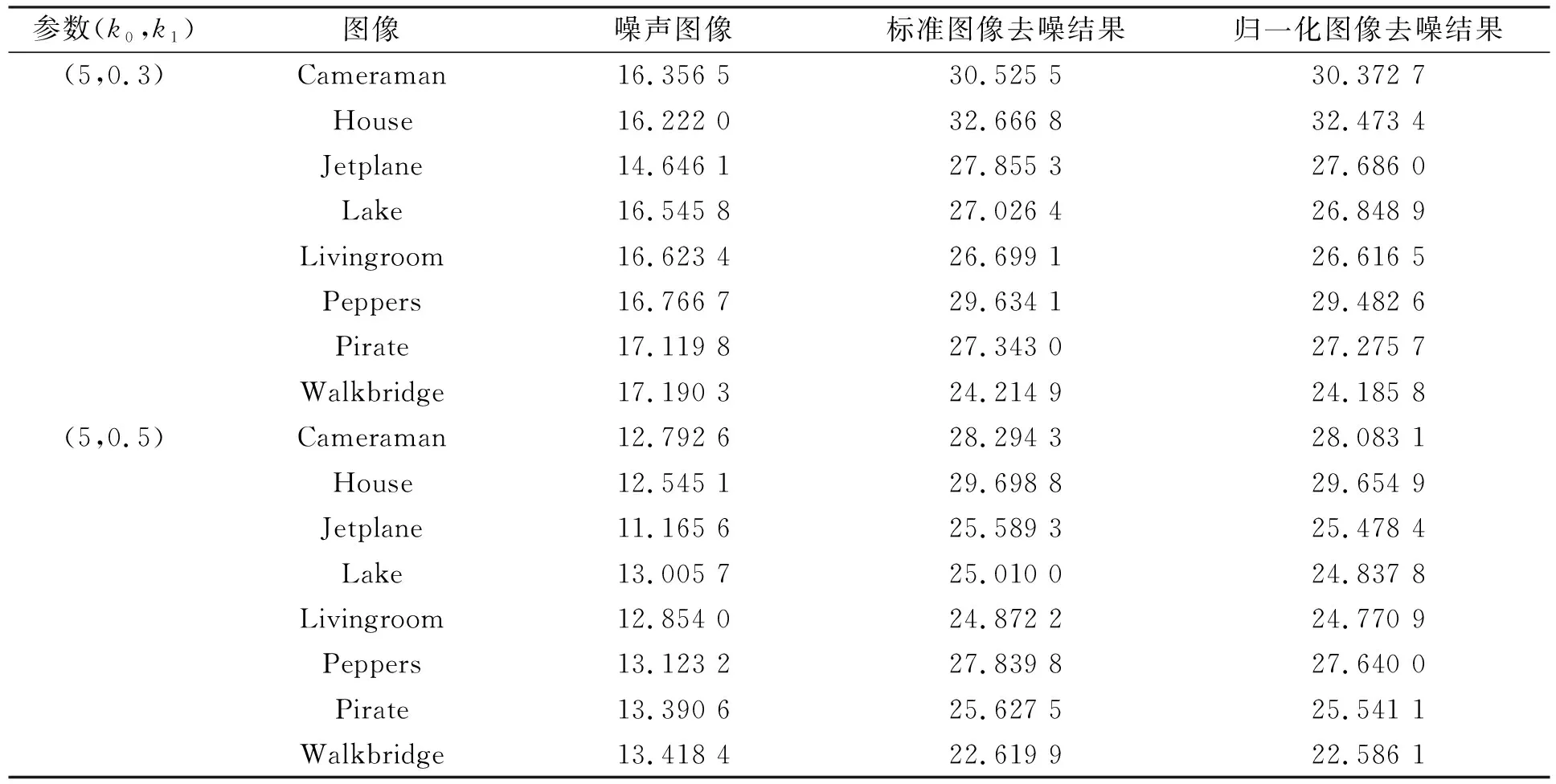
表1 乘性噪聲占主要程度時不同圖像下的PSNR對比

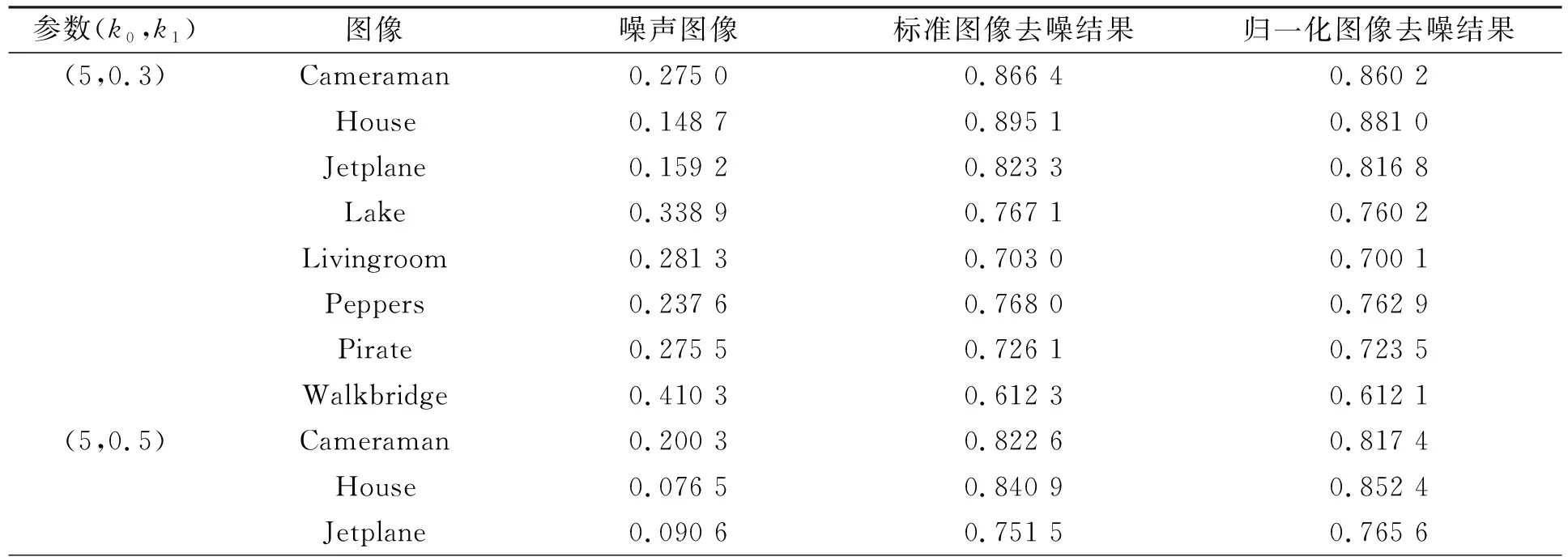
表2 乘性噪聲占主要程度時不同圖像下的SSIM對比

續表2

其次,設置適當的參數使噪聲占比剛好相反,加性噪聲程度相對較大而乘性噪聲占比較小,此時設置的兩組參數分別為(k0,k1)=(25,0.01)和(k0,k1)=(25,0.05).得到的圖像PSNR值和SSIM值分別列于表3和表4.

表3 加性噪聲占主要程度時不同圖像下的PSNR對比

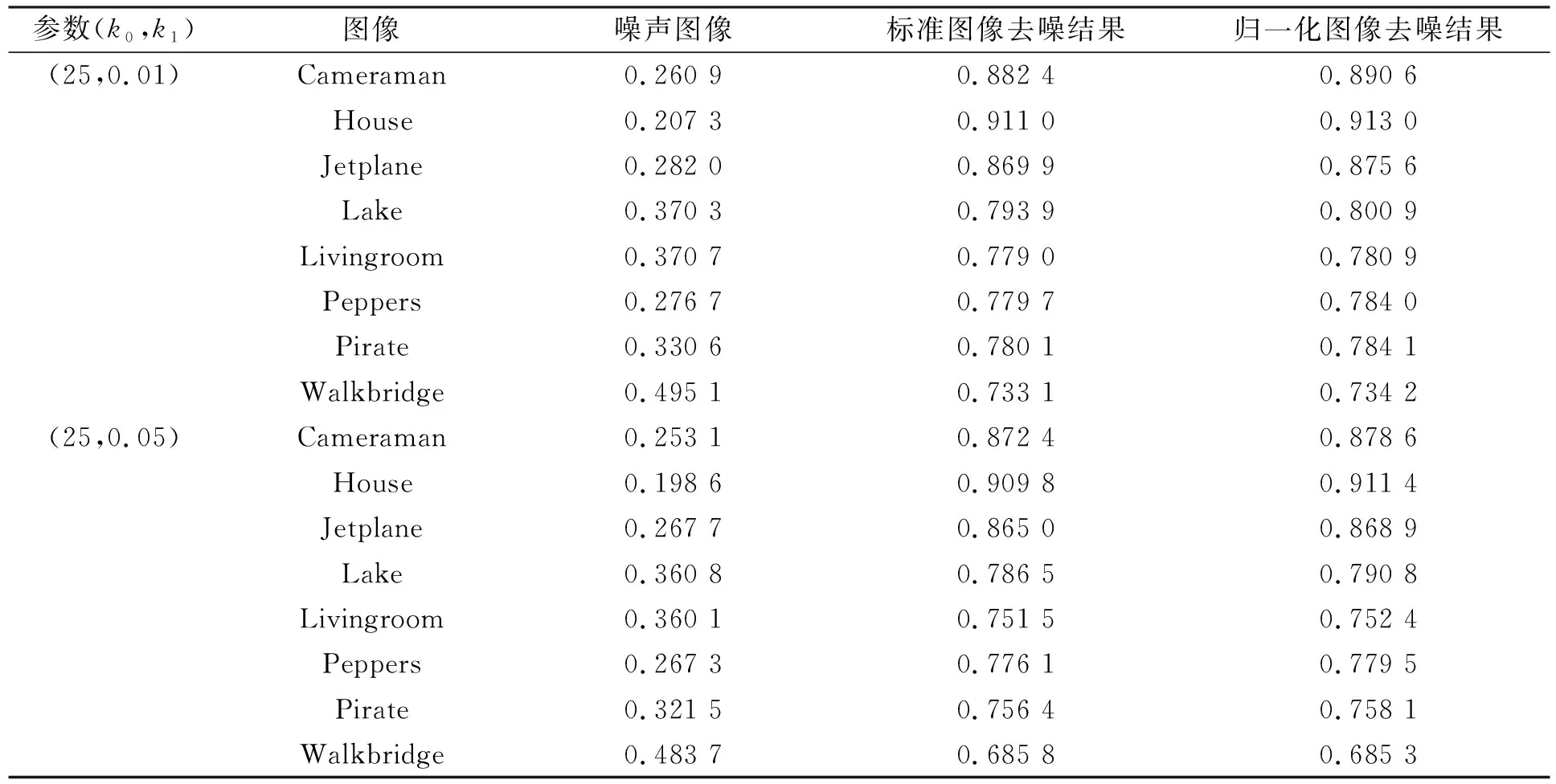
表4 加性噪聲占主要程度時不同圖像下的SSIM對比

為更直觀地觀察圖像去噪的細節部分,本文給出Cameraman圖像在(k0,k1)=(5,0.3)和(k0,k1)=(25,0.05)兩組參數下的噪聲圖像和不同表示模式下去噪后的圖像結果,分別如圖4和圖5所示.

圖4 (k0,k1)=(5,0.3)時Cameraman圖像不同模式去噪結果對比Fig.4 Comparison of denoising results for different modes of Cameraman images when (k0,k1)=(5,0.3)

圖5 (k0,k1)=(25,0.05)時Cameraman圖像不同模式去噪結果對比Fig.5 Comparison of denoising results for different modes of Cameraman images when (k0,k1)=(25,0.05)

在乘性噪聲參數相對較大的情況下,乘性噪聲在圖像的噪聲中占主導地位,如果乘性噪聲參數估計相對較準確,則對應的去噪結果就相對較好.反之,在加性噪聲程度較大的情況下,加性噪聲參數估計的準確性會直接影響去噪結果的優劣.表1的結果表明,在乘性噪聲參數相對較大的情況下,標準像素表示的圖像去噪結果比歸一化后圖像結果的PSNR值更高,即前者的結果更接近于原始圖像.表2中標準像素表示圖像的SSIM值一般較高則表示其圖像的結構信息優于歸一化后的圖像,說明標準像素圖像乘性噪聲參數的估計更準確.表3和表4的結果則表明在加性噪聲程度較大時,實驗得到的結果與之前的結果剛好相反,歸一化后圖像的去噪結果更好,說明其加性噪聲參數的估計更準確.本文實驗結果與定理3吻合,表明本文理論分析的結果正確.

綜上所述,針對廣義噪聲模型的噪聲參數估計問題,本文利用Fisher信息以及相關的漸近正態性給出了極大似然估計參數精度的理論分析.結果表明,在不同的圖像表現模式下,估計得到的兩類噪聲的方差有較大差別: 對于像素位于0～255內的標準圖像,其信號依賴噪聲的精度較高,加性噪聲的誤差較大;對于像素位于0～1內的歸一化后的圖像,參數的精度結果則剛好相反.實驗表明,本文的理論分析結果符合圖像噪聲參數的預測規律.