具時滯的捕食-食餌共生模型的Hopf分支

高 鶴,李秀玲

(吉林財經(jīng)大學 應用數(shù)學學院,長春 130117)

0 引 言

在自然界中,兩個生物種群之間的相互關系有捕食者與被捕食者、寄生關系、競爭關系、互惠共存關系等.如果兩個物種之間的相互作用對這兩個物種都有利,則兩個物種之間的共生關系稱為互惠共生的.互惠共生可通過兩種方式幫助獵物: 一是提高獵物的生長速度;二是阻止捕食者捕食獵物.在第二種情形中,關于時滯對種群動力系統(tǒng)影響的研究目前已有很多結(jié)果,例如: Ojha等[1]給出了一個考慮休眠時滯的浮游生物動力學模型;Djilali等[2]分析了一個捕食-食餌擴散模型的復雜動力學行為;Lavanya等[3]提出了具有食肉動物和捕食者孕育時滯的Holling-Ⅱ型捕食者-食餌模型,并研究了所有平衡點的存在性,以及時滯模型的局部穩(wěn)定性和Hopf分支.目前,關于捕食者食餌共生系統(tǒng)的研究已有一些結(jié)果[4-12],但對于具有時滯的捕食者食餌共生模型系統(tǒng)的研究文獻報道較少.本文在文獻[13-14]的基礎上,討論棉蚜、螞蟻、瓢蟲之間的種間關系.在棉田中,棉蚜是主要害蟲之一,它們通過吸食汁液、傳染病菌使棉花滋生霉菌,植株矮小,葉片變小,從而導致棉花大量減產(chǎn),造成重大經(jīng)濟損失.隨著農(nóng)藥的大量應用,棉蚜的抗藥性逐漸增強,此時需通過引入天敵進行防治.瓢蟲以棉蚜為食,螞蟻會驅(qū)趕瓢蟲,從而獲得更多棉蚜分泌的營養(yǎng)物質(zhì),因此棉蚜、螞蟻、瓢蟲三者相互制約,構(gòu)成了捕食-食餌共生系統(tǒng).通過控制三者的數(shù)量關系可解決棉田蟲害問題,從而更好地保護生態(tài)環(huán)境平衡.以食餌的發(fā)育時間和共生者的發(fā)育時間作為時滯,考慮如下具雙時滯的捕食-食餌共生模型:

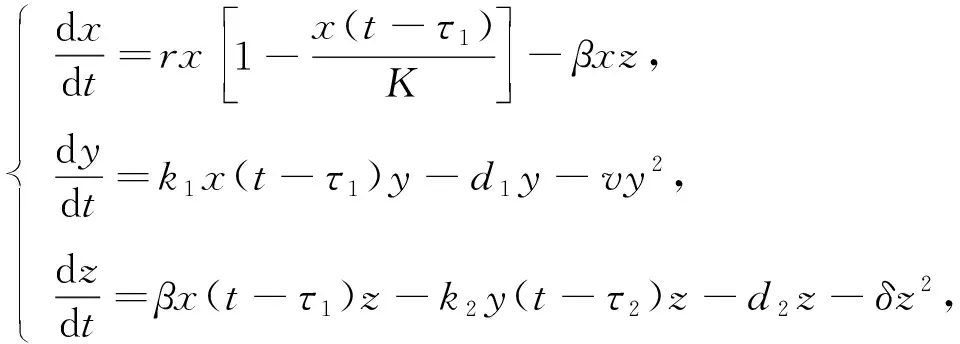
(1)

其中x(t),y(t),z(t)分別表示食餌的種群密度、共生者的種群密度和捕食者的種群密度,r表示食餌的內(nèi)稟增長率,K表示環(huán)境能維持的食餌最大數(shù)量,β表示捕食者對食餌的轉(zhuǎn)化率,k1表示食餌對共生者的共生效應,d1表示共生者的自然死亡率,v表示共生者因擁擠而導致的死亡率,k2表示共生者對捕食者的驅(qū)趕效應,d2表示捕食者的自然死亡率,δ表示捕食者因種群內(nèi)部競爭導致的死亡率,τ1,τ2分別表示食餌的發(fā)育時間和共生者的發(fā)育時間.所有參數(shù)都是正常數(shù),考慮到其實際生物學意義,發(fā)育時間只對其中一些變量有影響,死亡率不受時滯影響.本文考慮雙時滯對模型(1)的影響,首先,給出系統(tǒng)平衡點的穩(wěn)定性及Hopf分支的存在性;其次,利用規(guī)范型理論和中心流形定理給出Hopf分支方向和分支周期解的穩(wěn)定性;最后,利用Mathematica軟件進行數(shù)值模擬,驗證所得結(jié)論的正確性.通過對模型結(jié)果的分析和討論,給出模型物種之間的基本關系,從而對棉田的生物防治提供一定的理論基礎.

1 系統(tǒng)內(nèi)部平衡點的穩(wěn)定性和Hopf分支的存在性

令系統(tǒng)(1)各等式右邊為零,可得系統(tǒng)(1)的內(nèi)部正平衡點E=(x*,y*,z*),其中

系統(tǒng)(1)在平衡點E=(x*,y*,z*)處的Jacobi矩陣為

其中

a22=k1x*-d1-2vy*,a33=βx*-k2y*-d2-2δz*,

系統(tǒng)(1)在平衡點E=(x*,y*,z*)處對應的特征方程為

λ3+P02λ2+P01λ+P00+(P12λ2+P11λ+P10)e-λτ1+P20e-λ(τ1+τ2)=0,

(2)

其中

P00=-a11a22a33,P01=a11a22+a11a33+a22a33,

P02=-a11-a22-a33,P10=a22a13b31-a22a33b11,

P11=b11a22+b11a33-a13b31,P12=-b11,P20=-a13b21c32.

根據(jù)時滯τ1和τ2取值的不同,下面分4種情形討論.

情形1)τ1=τ2=0.

此時,方程(2)可轉(zhuǎn)化為如下形式:

λ3+J12λ2+J11λ+J10=0,

(3)

其中

J10=P00+P10+P20,J11=P01+P11,J12=P02+P12.

假設:

(H1)J10>0,J11>0,J12>0,J12J11>J10.

根據(jù)Routh-Hurwitz穩(wěn)定性判據(jù),可得以下結(jié)論:

定理1當且僅當條件(H1)成立時,方程(3)的所有根都具有負實部,即系統(tǒng)(1)在正平衡點E=(x*,y*,z*)處是漸近穩(wěn)定的.

下面考慮時滯對系統(tǒng)(1)正平衡點E=(x*,y*,z*)穩(wěn)定性的影響.

情形2)τ1>0,τ2=0.

此時,方程(2)可轉(zhuǎn)化為

λ3+P02λ2+P01λ+P00+(P12λ2+P11λ+P10+P20)e-λτ1=0.

(4)

令λ=iω1(ω1>0)為方程(4)的根,分離實部和虛部可得

其中

于是可得

(5)

其中

θ10=-P00P10-P00P20,θ11=-P00P11+P01P11+P01P20,

θ12=-P01P11+P02P10+P02P20+P12P00,

θ13=P02P11-P10-P20-P01P12,θ14=P11-P02P12,θ15=P12,

將式(5)中兩式兩端取平方后再相加可得

(6)

其中

假設:

(H2)φ0<0或φ0≥0且Δ>0,s1>0,h(s1)≤0.

引理1當條件(H2)成立時,方程(5)存在正根.

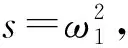
s3+φ2s2+φ1s+φ0=0.

(7)

再令

h(s)=s3+φ2s2+φ1s+φ0,

(8)

由式(8)可知

因此當s1>0,h(s1)≤0時,方程(7)有正根.

這里

令λ(τ1)=α(τ1)+iω(τ1)是方程(4)在時滯τ1=τ10處滿足α(τ1)=0,ω(τ1)=ω10的根.

假設:

(H3) 3s2+2φ2s+φ1>0.

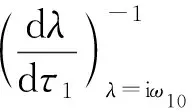
證明: 將方程(4)兩邊對τ1求導,可得

由方程(4)可得

(P12λ2+P11λ+P10+P20)e-λτ1=-λ3-P02λ2-P01λ-P00,

于是有

(9)

將λ=iω10代入式(9)可得

綜上,可得以下結(jié)論:

定理2對于系統(tǒng)(1),當τ1>0,τ2=0時,如果條件(H2),(H3)成立,則當τ1∈[0,τ10)時,系統(tǒng)(1)的平衡點E=(x*,y*,z*)是漸近穩(wěn)定的;當τ1>τ10時,系統(tǒng)(1)的平衡點E=(x*,y*,z*)是不穩(wěn)定的;當τ1=τ10時,系統(tǒng)(1)在正平衡點E=(x*,y*,z*)處產(chǎn)生Hopf分支.

情形3)τ1=0,τ2>0.

此時,方程(2)可轉(zhuǎn)化為如下形式:

λ3+F02λ2+F01λ+F00+F10e-λτ2=0,

(10)

其中

F00=P00+P10,F01=P01+P11,F02=P02+P12,F10=P20.

令λ=iω2(ω2>0)為方程(10)的根,分離實部和虛部可得

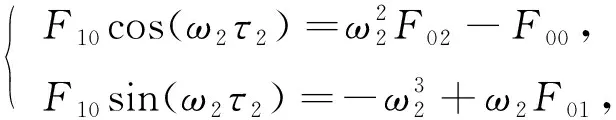
(11)

將式(11)中兩式兩端取平方后再相加可得

(12)

假設:

(H4)φ5<0或φ5≥0且Δ2>0,r1>0,h(r1)≤0.

引理3若條件(H4)成立,則方程(12)存在正根.

證明: 令

則方程(12)變?yōu)?/p>

r3+φ3r2+φ4r+φ5=0.

(13)

再令

g(r)=r3+φ3r2+φ4r+φ5.

由g(r)可知,

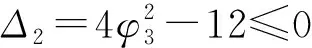
因此當r1>0,g(r1)≤0時,方程(10)有正根.

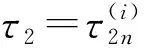
令λ(τ2)=α(τ2)+iω(τ2)是方程(12)在時滯τ2=τ20處滿足α(τ2)=0,ω(τ2)=ω20的根.

假設:

(H5) 3r2+2φ3r+φ4>0.

證明: 將式(10)兩邊對τ2求導,得

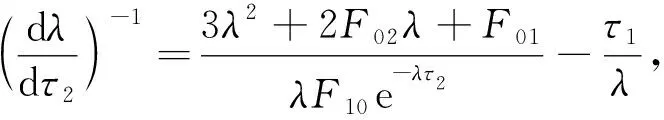
(14)

由于F10e-λτ2=-λ3-F02λ2-F01λ-F00,將λ=iω20代入式(14)可得

綜上,可得以下結(jié)論:

定理3對于系統(tǒng)(1),當τ1=0,τ2>0時,若條件(H4),(H5)成立,則當τ2∈[0,τ20)時,系統(tǒng)(1)的平衡點E=(x*,y*,z*)是漸近穩(wěn)定的;當τ2>τ20時,系統(tǒng)(1)的平衡點E=(x*,y*,z*)是不穩(wěn)定的;當τ2=τ20時,系統(tǒng)(1)在平衡點E=(x*,y*,z*)處產(chǎn)生Hopf分支.

情形4)τ1>0,τ2∈(0,τ20),即把τ2限制在其穩(wěn)定區(qū)間內(nèi),將τ1作為參數(shù).

系統(tǒng)(1)在平衡點E=(x*,y*,z*)處對應的特征方程為

λ3+P02λ2+P01λ+P00+(P12λ2+P11λ+P10)e-λτ1+P20e-λ(τ1+τ2)=0.

(15)

令λ=iω3(ω3>0)為方程(15)的根,則

其中

進一步可得

(16)

其中

e2=2P12P20,e1=2P11P20,e0=-2P10P20.

假設:

引理5若條件(H6)成立,則方程(16)至少存在一個正根.

證明: 令

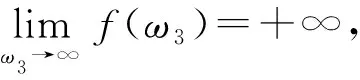
令λ(τ1)=α(τ1)+iω(τ1)是方程(15)在時滯τ1=τ30處滿足α(τ1)=0,ω(τ1)=ω30的根.

假設:

(H7)QRPR+QIPI>0.

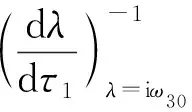
證明: 將式(15)對τ1求導,得

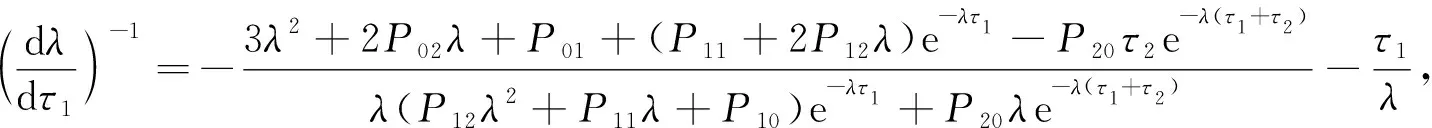
(17)

將λ=iω30代入式(17)可得

其中

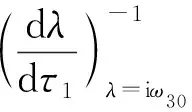
綜上,可得以下結(jié)論:

定理4對于系統(tǒng)(1),當τ1>0,τ2∈(0,τ20)時,如果條件(H6),(H7)成立,則當τ1∈[0,τ30)時,系統(tǒng)(1)的平衡點E=(x*,y*,z*)是漸近穩(wěn)定的;當τ1>τ30時,系統(tǒng)(1)的平衡點E=(x*,y*,z*)是不穩(wěn)定的;當τ1=τ30時,系統(tǒng)(1)在平衡點E=(x*,y*,z*)處產(chǎn)生Hopf分支.

2 Hopf分支的方向和穩(wěn)定性

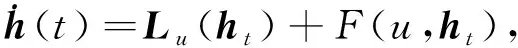
(18)

其中

ht=(h1,h2,h3)T∈C([-1,0],3),

由Riesz表示定理可知,存在3×3的矩陣函數(shù)η(θ,u)和變量θ∈[-1,0],滿足

事實上,可以選擇

對于φ∈C([-1,0],3),定義

則式(1)可轉(zhuǎn)化為

(19)

定義A的伴隨算子A*為

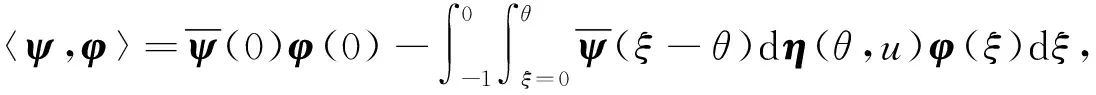
直接計算可得如下結(jié)論:

根據(jù)文獻[15],計算相關系數(shù)如下:

其中

這里E1,E2滿足

于是,經(jīng)計算可得

因此,系數(shù)μ2,β2,τ3決定了Hopf分支的性質(zhì).其中μ2決定Hopf分支的方向,當μ2>0,τ1>τ30時,系統(tǒng)在平衡點附近發(fā)生超臨界Hopf分支;當μ2<0,τ1<τ30時,系統(tǒng)在平衡點附近發(fā)生亞臨界Hopf分支.且在上述相應時滯范圍內(nèi)存在周期解,當T2>0(或T2<0)時,周期解的周期增加(或減少);當β2<0(β2>0)時,周期解是漸近穩(wěn)定的(或不穩(wěn)定的).

3 數(shù)值模擬

對于系統(tǒng)(1),取如下參數(shù)值:r=0.1,K=40,k1=0.03,k2=0.02,d1=0.02,d2=0.04,β=0.02,δ=0.006,v=0.05,則系統(tǒng)(1)可變?yōu)?/p>

圖1 當τ1=τ2=0時,系統(tǒng)(1)的時間序列曲線Fig.1 Time series curves of system (1) when τ1=τ2=0

經(jīng)計算可得該系統(tǒng)的正平衡點為E=(7.087,3.514,4.114 3).顯然有J10=0.000 982,J11=0.020 3,J12=0.235,J12J11=0.004 8>J10.根據(jù)Routh-Hurwitz穩(wěn)定性判據(jù)可知,當τ1=τ2=0時,該系統(tǒng)的正平衡點E是漸近穩(wěn)定的,如圖1所示.

當τ1>0,τ2=0時,經(jīng)計算可得τ10=10.291 4.當τ1<τ10時,該系統(tǒng)的平衡點E是漸近穩(wěn)定的,如圖2所示.當τ1>τ10時,該系統(tǒng)的平衡點E是不穩(wěn)定的,此時在平衡點E處出現(xiàn)Hopf分支,如圖3所示.

當τ1>0,τ2>0時,通過計算可知條件(H6)和(H7)均滿足.選取τ1=6<τ30=8.574 7,τ2=5∈(0,τ20)=(0,21.501 7),則系統(tǒng)的平衡點E是漸近穩(wěn)定的,如圖4所示.選取τ1=8.63>τ30=8.574 7,τ2=5,則系統(tǒng)的平衡點E是不穩(wěn)定的,此時在平衡點E處發(fā)生Hopf分支,如圖5所示.

圖2 當τ1=5,τ2=0時,系統(tǒng)(1)的時間序列曲線(A),(B),(C)及相圖(D)Fig.2 Time series curves (A),(B),(C) and phase diagram (D) of system (1) when τ1=5,τ2=0

圖3 當τ1=10.292,τ2=0時,系統(tǒng)(1)的時間序列曲線(A),(B),(C)及相圖(D)Fig.3 Time series curves (A),(B),(C) and phase diagram (D) of system (1) when τ1=10.292,τ2=0

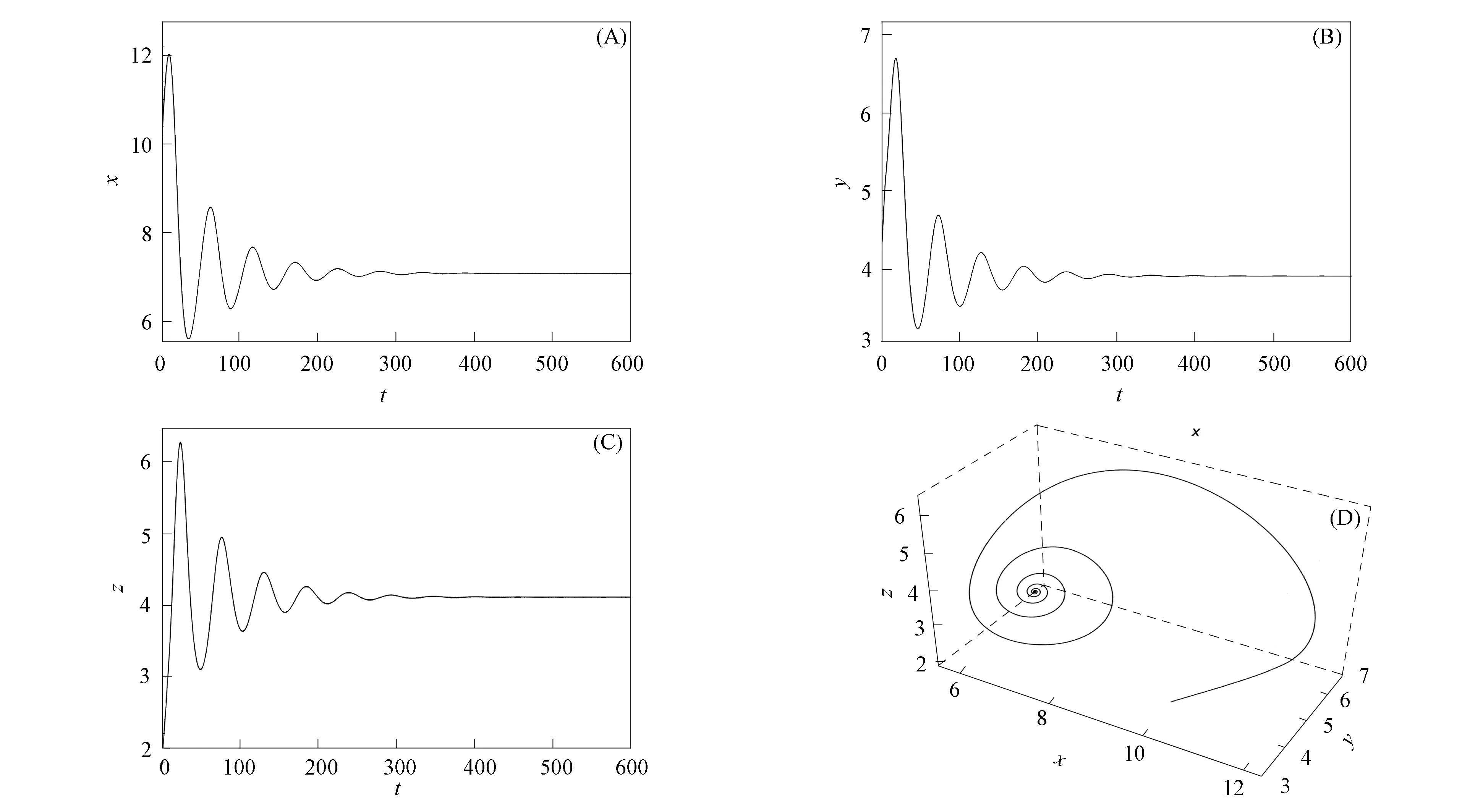
圖4 當τ1=6,τ2=5時,系統(tǒng)(1)的時間序列曲線(A),(B),(C)及相圖(D)Fig.4 Time series curves (A),(B),(C) and phase diagram (D) of system (1) when τ1=6,τ2=5

圖5 當τ1=8.63,τ2=5時,系統(tǒng)(1)的時間序列曲線(A),(B),(C)及相圖(D)Fig.3 Time series curves (A),(B),(C) and phase diagram (D) of system (1) when τ1=8.63,τ2=5

綜上所述,本文對一類捕食-食餌共生模型引入了食餌和共生者的發(fā)育時間兩個時滯.首先,得到了模型平衡點的穩(wěn)定性及Hopf分支存在性的充分條件,結(jié)果表明,在一定的條件下,系統(tǒng)的平衡點是漸近穩(wěn)定的,且當時滯超過一定閾值后,系統(tǒng)在平衡點處發(fā)生Hopf分支,并得到了一系列的周期解;其次,利用規(guī)范型理論和中心流形定理,給出了上述模型的Hopf分支方向和分支周期解的穩(wěn)定性;最后,利用Mathematica軟件對該模型進行數(shù)值模擬,驗證了所得結(jié)論的正確性.