基于神經隨機微分方程的期權定價

季鑫緣,董建濤,陶 浩

(1.西安電子科技大學 數學與統計學院,西安 710126;2.中電科思儀科技股份有限公司,山東 青島 266555;3.西安電子科技大學 網絡與信息安全學院,西安 710126)

期權定價是金融數學和金融工程領域的研究熱點,研究期權價格的建模和計算方法對于理解期權價格走勢、創造新的金融工具及評估與特定期權相關的風險至關重要.經典Black-Scholes模型[1]作為期權定價的基礎,先假設資產回報率和波動率均為常數,然后通過風險中性等價鞅測度下的折現計算期權價格.基于Black-Scholes模型,可以計算出期權價格的封閉式解.但Black-Scholes模型在實際計算期權價格時表現不佳[2].例如: Black-Scholes模型假設無交易成本,但事實上交易時存在手續費;Black-Scholes模型中假設波動率和無風險利率為常數,但事實上它們通常是不固定的.

目前,數據密集型的機器學習方法已廣泛應用于醫療保健、教育、制造和金融建模等領域.作為機器學習的重要組成部分,深度學習方法比傳統的機器學習方法更適應高維、非線性的復雜數據[3],但解決此類問題通常需要以大型數據集為依托,而獲取大量的期權價格數據用于神經網絡的訓練又需要非常高的成本.因此,本文考慮將深度學習與隨機微分方程(SDE)相結合,把Black-Scholes模型中的漂移項和擴散項參數化為神經網絡,既保留SDE的一般結構,又通過SDE的約束減少訓練神經網絡所需的數據.通過選取真實的日后復權股票價格數據作為訓練集和測試集進行實驗,經過反向傳播不斷更新網絡的權重使訓練損失收斂,最終得到的網絡在預測股票價格方面具有更高的準確度,進而實現對期權更準確的定價.

對于一個目標期權的價格,在每個時刻股票價格數據不可觀測時,無法再通過神經隨機微分方程(NSDE)的方法對其進行學習.由于目標期權和已知股票價格的期權都可以用其風險中性等價鞅測度表示,因此本文考慮把目標期權價格和一個已知期權價格的差值限制在它們的Wasserstein距離內,以實現對期權價格的估計.

1 模型建立

1.1 建立神經隨機微分方程模型

設(Ω,F,P,F=(Ft)t≥0)為一個過濾概率空間,其中過濾 F=(Ft)t≥0滿足通常條件,B=(Bt)t≥0為該概率空間下的一個標準布朗運動.假設股票價格過程(St)t≥0滿足如下隨機微分方程:

dSt=μStdt+σStdBt,

(1)

其中回報率μ∈,波動率σ>0.實際應用中,回報率和波動率通常很難估計,尤其是回報率μ.因此本文采用NSDE的方法估計回報率和波動率,下面假設和分別為NSDE的漂移參數和波動參數,即NSDE可表述為

(2)

其中St表示由NSDE得到的t時刻的股票價格,θμ和θσ分別表示深度學習中未知的權重和偏移參數.

則對任一初始值X0∈,NSDE存在唯一強解.

假設以某支股票為標的資產的期權合約到期日為T,則對于t∈[0,T],可將式(1)寫成如下積分形式:

(3)

St=S0exp{σBt+(μ-σ2/2)t}.

(4)

進一步,假設 Q表示與自然概率測度 P等價的風險中性等價鞅測度,則由資產定價第二基本定理可知,在無套利條件下,與 P等價的風險中性等價鞅測度存在且唯一[5].在測度Q下,貼現過程是鞅,本文以歐式看漲期權為例,其他類型的期權可用類似的方法建模和分析.根據Girsanov定理,BQt表示測度Q下的標準布朗運動:

BQt=Bt+κt,

其中κ=(μ-r)/σ表示風險的市場價格,r為無風險收益率[6].歐式看漲期權在0時刻的價格可表示為

P0=EQ[e-rTφ(ST)],

(5)

其中φ(ST)=(ST-K)+,K為行權價格,φ(·)為正部函數.下面通過測度變換技術,將定義在測度 Q下的歐式看漲期權價格重新表示為在自然概率測度 P下的表達式.

引理2若以式(1)中的St作為歐式看漲期權標的股票的價格,則該歐式看漲期權在0時刻的價格可表示為

(6)

其中t∈[0,T].特別地,對于零利率(r=0),有

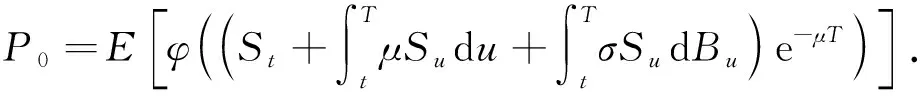
(7)

證明: 由式(4)得

將κ=(μ-r)/σ代入式(8)并化簡,得

(9)

將式(3)代入式(9),并展開ST項即可證明式(6).證畢.

(10)

特別地,當r=0時可將式(10)化簡為

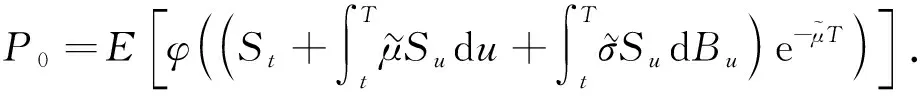
(11)

1.2 構建網絡結構

對于估計μ,建立含有3個隱含層的簡單神經網絡訓練參數μ,其中θμ=(Wμ,bμ)為漂移網絡的權重矩陣和偏移參數.對于估計σ,建立包含4個隱含層的神經網絡訓練參數σ,其中θσ=(Wσ,bσ)表示擴散網絡的權重矩陣和偏移參數[7].設兩個網絡中每個隱含層的節點數均為100個,分別建立如圖1所示的網絡結構.

圖1 神經網絡結構Fig.1 Structure of neural network

(12)

圖2 Tanh激活函數及其導函數圖像Fig.2 Tanh activation function and itsderivative function images

Tanh激活函數圖像如圖2所示.考慮將式(2)隨機微分方程的解離散化表示,將時間區間[0,T]等間距劃分為N份,當時間間隔足夠小時,股票價格過程有如下迭代形式[8]:

圖3 NSDE結構Fig.3 Structure of NSDE

2 實證分析

2.1 訓練神經隨機微分方程模型

圖4 股票價格數據Fig.4 Stock price data

實驗選取真實的股票價格數據作為輸入,以圖4中2012—2015年的958個交易日的日后復權股票價格數據為訓練集,2016年的前200個交易日的日后復權股票價格數據為測試集,以訓練后t時刻的股票價格作為網絡的輸出項.在標的資產為單一股票的情形下,在神經網絡前向傳播的過程中,輸入層將初始價格數據傳輸至隱藏層,通過梯度下降不斷訓練漂移和擴散參數,最終在輸出層通過激活函數得到模擬的股票價格數據.

訓練算法的過程實際是通過每次迭代后計算損失,然后交替更新漂移網絡與擴散網絡中的參數.Zhou等[9]研究表明,損失函數在神經網絡模型的訓練中具有重要作用,神經網絡的精度通常也受損失函數的限制.在深度學習的回歸問題中,通常可選擇均方誤差 (MSE) 或平均絕對誤差(MAE) 作為訓練的損失函數,考慮到使用MAE函數訓練收斂速度較慢,為保持模型的整體性能,本文選擇用MSE函數計算損失[10].由于股票價格走勢是非凸函數,因此對網絡權重的更新采用隨機梯度下降法.Hardt等[11]研究表明,雖然隨機梯度下降法在解決非凸函數的優化問題上沒有理論保證,但其仍然是一種快速穩定的神經網絡訓練算法.

設L表示訓練的損失函數,其數學表達式為

(14)

模型的校準問題通常可轉化為解決以下最小二乘問題,以找到網絡中最優的參數θμ和θσ:

(15)

其中θμ=(Wμ,bμ),θσ=(Wσ,bσ).下面以Wμ中的第一個元素W1為例給出計算損失函數關于參數偏導數的過程:

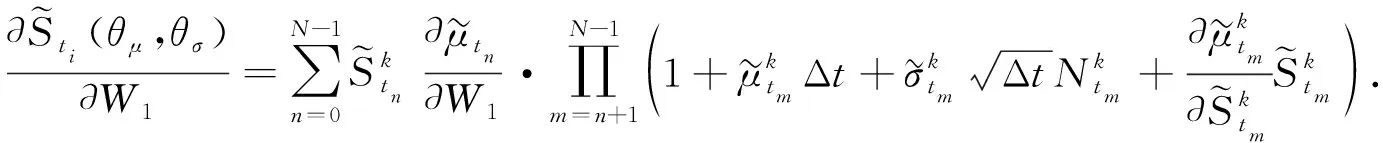
(16)

式(16)右端包含許多項的乘積,如果連乘項中某一項的值很小,則可能導致整體為零,稱為梯度消失.由于式(16)中的連乘項內每項都包含一個常數1,因此乘積不可能接近于0,這種結構解決了梯度消失的問題,使訓練更穩定.

算法1PyTorch神經網絡NSDE模型.

輸入: 價格數據矩陣x∈958×1,漂移網絡Drift,擴散網絡Diffusion,迭代次數為100;初始學習率α= 0.001;損失函數為

輸出: 每次迭代的損失值,訓練后漂移網絡和擴散網絡隱含層的權重和偏移參數Wμ*,bμ*,Wσ*,bσ*,訓練后的股票價格數據(Si)i∈[1,958].

步驟1) 隨機初始化漂移網絡和擴散網絡隱含層的參數:Wμ(0),bμ(0),Wσ(0),bσ(0).

步驟2) 構造一個NSDE類、前向傳播:

將漂移網絡Drift和擴散網絡Diffusion添加到迭代更新計算股票價格的表達式中,

for迭代次數k=0 to 99 do

end for

步驟3) 計算損失:

for迭代次數k=0 to 99 do

end for

步驟4) 反向傳播、更新漂移和擴散網絡的參數:

for迭代次數k=0 to 99 do

loss.backward( )

end for

步驟5) 動態調整學習率:

for每次迭代epoch=1,2,…,99 do

end for.

設迭代次數為100次,迭代完成時損失函數收斂,即經過訓練網絡達到了損失很小的狀態,使用NSDE模型模擬的股票價格準確率很高.整個實驗是在PyTorch中完成的,算法流程如算法1,唯一調優的超參數是優化器中的初始學習率.為使實驗能夠加速收斂,選擇動態變化的學習率,隨著迭代次數的增加學習率越來越小.實驗平臺采用具有Geforce RTX GPU的Linux服務器,內存64 GB,編程語言為Python.

2.2 實證分析結果

為檢驗NSDE模型的性能進行一個數值實驗,在測試集上分別使用NSDE模型和Black-Scholes(BS)模型模擬股票價格.NSDE模型用的回報率和波動率是在訓練集上訓練得到的,Black-Scholes模型中的回報率和波動率采用訓練集數據的平均回報率和歷史波動率.對比兩個模型的預測精度時,采用MAE,MSE,RMSE(均方根誤差)和R24個評價指標.

NSDE模型經過訓練得到的回報率和波動率如圖5所示.由圖5可見,NSDE模型經過訓練后的回報率和波動率隨時間和股票價格時刻變動,并非像Black-Scholes模型的假設那樣是常數.

圖5 NSDE模型訓練后的回報率(A)和波動率(B)Fig.5 Return rate (A) and volatility (B) of NSDE model after training

圖6 測試集上NSDE模型與Black-Scholes模型預測結果對比Fig.6 Comparison of prediction results of NSDE model and Black-Scholes model on test set

測試集上NSDE模型與Black-Scholes模型預測結果對比如圖6所示.由圖6可見: 由Black-Scholes模型在未來200 d(測試集)預測的股票價格明顯不接近真實值,但NSDE模型的預測效果很好;NSDE模型的預測誤差曲線也整體位于Black-Scholes模型預測誤差曲線的下方.為更具體地比較兩個模型的差異,表1列出了NSDE模型和Black-Scholes模型的損失評價指標.表1中的結果證實了根據圖像得出的結論是正確的,在測試集上本文提出的NSDE模型的MAE,MSE和RMSE均小于Black-Scholes模型對應的值,而R2高于Black-Scholes模型的計算值.說明NSDE模型預測的股票價格更接近真實股票價格,預測效果明顯優于Black-Scholes模型.

表1 NSDE模型和Black-Scholes模型測試集股票價格預測結果對比

3 近似目標期權價格

無論是Black-Scholes模型還是NSDE模型,都依賴于股票的一些基本信息,如每個時刻股票的價格數據,當無法觀測每個時刻的股票價格時,兩個模型都會失效,其對應的期權價格也無法計算.下面考慮在未知收益率,僅已知波動率和初始時刻股票價格數據的情況下,對期權價格進行估計和預測.

Wasserstein距離目前在統計和機器學習中應用廣泛[12].例如:lvarez-Esteban等[13]研究了一種基于截尾分布之間的L2-Wasserstein距離的分布相似性分析方法,通過實例驗證了這種數據驅動的方法可使分布之間的相似性最大化;Arjovsky等[14]將GAN與Wasserstein距離結合,提出的WGAN能通過訓練鑒別器達到最優性來連續估計EM(earth-morer)距離,解決了GAN存在的主要訓練問題.本文利用Wasserstein距離可作為概率測度之間度量的性質,考慮將期權價格用風險中性等價測度表示,最后給出一個關于目標期權價格的約束.

3.1 目標期權價格表示

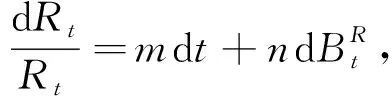
(17)

其中回報率m∈,波動率n>0.設目標期權0時刻的價格為Q0,可以用與 P對應的風險中性等價鞅測度 H表示為

Q0=EH[e-rTφ(RT)],

(18)

其中φ(RT)=(RT-K)+,兩份期權具有相同的到期日T和行權價格K,φ(·)為正部函數.由引理2可得Q0在自然概率測度 P下的表達式為

(19)

由于回報率m是未知的,除R0外Rt是不可觀測的,因此無法再使用NSDE模型訓練回報率和波動率.下面考慮用已知的期權價格P0預測估計未知的期權價格Q0,考慮到P0和Q0都可以在風險中性等價鞅測度下計算,因此選擇使用Wasserstein距離作為約束,給出期權價格的一個估計.

3.2 目標期權價格近似誤差

下面給出用P0近似Q0的近似誤差.

定理1目標期權的價格Q0可以用包含其標的資產且到期日和行權價格都相同的期權價格P0近似,近似誤差為

erT|P0-Q0|≤W1(νQS,νHR),

(20)

證明: 首先注意到

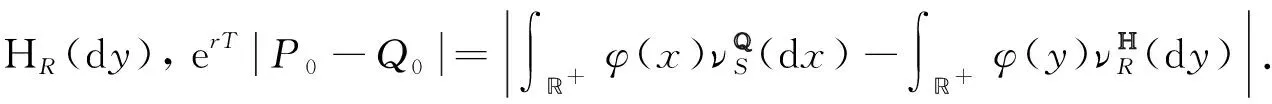
(21)

從而證明了不等式成立.由于在風險中性等價測度下,收益率等于無風險利率,所以對任意的x>0,有

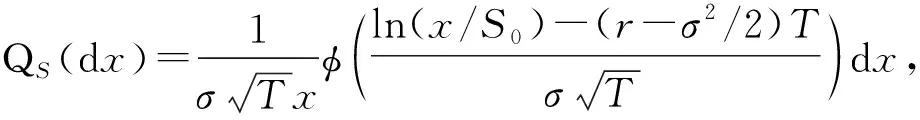
證畢.

其中:W1(νQS,νHR)表示νQS與νHR之間的Wasserstein-1距離;

下面給出簡化后近似誤差計算公式的結果.

推論1目標期權的價格Q0可以用P0近似,近似誤差為

(23)

4 結果與討論

基于現有的Black-Scholes模型進行期權定價,在實際應用中存在回報率和波動率難估計的問題.如果考慮簡單地將深度學習理論應用于期權定價,則需要通過獲取大型數據集為網絡提供信息,從而帶來較大的計算復雜度.本文考慮將經典Black-Scholes模型與深度學習相結合,將原來的回報率和波動率參數化為神經網絡,建立NSDE模型.在實驗中選取2012—2016年的股票價格數據用來訓練和測試網絡,實驗結果表明,用NSDE模型訓練可以得到動態變化的漂移項和擴散項,該模型預測效果優于Black-Scholes模型.當回報率未知且除初始時刻外每時刻股票價格不可觀測時,NSDE模型不再能通過訓練預測股票價格,因此本文在理論上提供了另一種估計方法,用一個已知期權的價格近似目標期權價格,并給出了近似誤差的計算公式.

事實上,Black-Scholes模型在期權定價中出現的問題還有很多,例如,Black-Scholes模型假設波動率是常數,但實際市場中波動率常呈現“微笑”形狀,因此對于NSDE模型可以添加針對波動率的約束進行優化.另一方面,在NSDE模型中采用隨機梯度下降(SGD)法對網絡權重進行更新,但SGD算法可能會導致收斂速度慢或陷入局部最小值等問題[15],而且如何選擇合適的學習率作為初始值較困難.Shi[16]已經證明了學習率和動量系數這兩個超參數在非凸優化問題中對線性收斂速度的重要作用,帶動量的隨機梯度下降可以加速收斂.因此,用帶動量的隨機梯度下降法替換SGD算法可以作為后續優化網絡的主要工作.