相對羅巴算子的擬跡函數方法和上同調

徐森榮,譚易蘭,趙 嘉

(1.江蘇大學 數學科學學院,江蘇 鎮江 212013;2.南通大學 理學院,江蘇 南通 226019)

代數的算子包括Nijenhuis算子和羅巴算子等,在量子場論、可積系統、數論等領域應用廣泛[1-2].3-李代數作為李代數的自然推廣,廣泛應用于幾何學、力學、弦論及M2-膜理論中,因此受到廣泛關注[3-6].3-李代數與李代數及Leibniz代數等有密切的聯系,例如,由李代數及其擬跡函數可以誘導3-李代數[7],并且3-李代數可以自然地誘導出Leibniz代數.

近年來,代數上算子的上同調理論研究也得到廣泛關注.文獻[8]研究了n-李代數的(n-1)-階形變和Nijenhuis算子的構造,證明了任意一個n-李代數上Nijenhuis算子的多項式仍然是Nijenhuis算子;文獻[9-10]分別構造了李表示對和3-李表示對上相對羅巴算子的上同調,并研究了其形變理論.

擬跡函數可以誘導相對羅巴算子.假設(G,ρ)是一個李表示對,τ∈G*是擬跡函數,T:V→G是(G,ρ)上的相對羅巴算子,則T也是擬跡函數τ誘導的3-李表示對(Gτ,ρτ)上的相對羅巴算子[11].基于此,本文先給出李表示對的相對羅巴算子的上同調群和擬跡函數誘導的3-李表示對的相對羅巴算子的上同調群在低階情形下的對應關系,再利用鏈映射構造出李表示對和誘導3-李表示對的相對羅巴算子的任意階數大于等于2的上同調群之間的同態.本文所有的線性空間和代數都在特征為零的域K上.

1 預備知識

定義1[7]設(G,[·,·])是一個李代數,令τ∈G*,如果

τ(x)τ([y,z])+τ(y)τ([z,x])+τ(z)τ([x,y])=0, ?x,y,z∈G,

(1)

則稱τ是李代數G上的擬跡函數.

李代數G上跡函數τ:G→K定義為τ([G,G])=0.文獻[7]證明了李代數G上一個線性函數是跡函數當且僅當Kerτ是G的理想;李代數G上一個線性函數是擬跡函數當且僅當Kerτ是G的子代數.因此,擬跡函數可視為跡函數的自然推廣.

定義23-李代數由一個向量空間G和一個三元線性運算[·,·,·]: ∧3G→G組成,且滿足如下基本恒等式:

[x,y,[z,w,t]]=[[x,y,z],w,t]+[z,[x,y,w],t]+[z,w,[x,y,t]], ?x,y,z,w,t∈G.

(2)

注1[7]設τ是李代數G上的擬跡函數.對?x,y,z∈G,定義三元線性括號

[x,y,z]τ∶=τ(x)[y,z]+τ(y)[z,x]+τ(z)[x,y],

τ([x,y,z]τ)=0, ?x,y,z∈G.

(3)

由文獻[7]可知,(G,[·,·,·]τ)為3-李代數,稱為由擬跡函數所誘導的3-李代數,簡記為Gτ.令(G,ρ)是G的李表示對.定義ρτ: ∧2G→Gl(V)為

ρτ(x,y)=τ(x)ρ(y)-τ(y)ρ(x),x,y∈G,

(4)

則(Gτ,ρτ)是由擬跡函數所誘導的3-李表示對.

定義4[9]設(G,ρ)是一個李表示對,若線性映射T:V→G滿足

[Tu,Tv]=T(ρ(Tu)(v)-ρ(Tv)(u)), ?u,v∈V,

則稱T是李表示對(G,ρ)上的相對羅巴算子.

下面給出李表示對相對羅巴算子的上同調[9].設G是李代數,T是李表示對(G,ρ)上的相對羅巴算子.在V上引入二元括號[·,·]T為

[u,v]T=ρ(Tu)v-ρ(Tv)u, ?u,v∈V.

定義ρT:V→Gl(G)為

ρT(u)(x)∶=[Tu,x]+Tρ(x)(u), ?x∈G,u∈V,

(5)

dρT(x)v=Tρ(x)v-[x,Tv], ?v∈V.

(6)

(7)

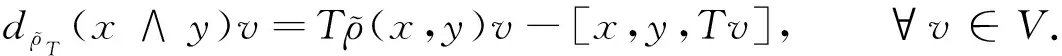
(8)

設G是李代數,T是李表示對(G,ρ)上的相對羅巴算子,則由式(7)給出的ρT是李代數(V,[·,·]T)上的表示.令τ是李代數G上的擬跡函數,則由注1知,(Gτ,ρτ)是擬跡函數誘導的3-李代數Gτ的3-李表示對.

引理1[11]若T是李代數G對應的李表示對(G,ρ)上的相對羅巴算子,則T也是3-李代數Gτ對應的3-李表示對(Gτ,ρτ)上的相對羅巴算子.

引理21) (V,[·,·,·]T)是3-李代數,這里[·,·,·]T定義為

[u,v,w]T=ρτ(Tu,Tv)w+ρτ(Tv,Tw)u+ρτ(Tw,Tu)v, ?u,v,w∈V;

(9)

(10)

注2由引理1可知,T是3-李代數Gτ對應的3-李表示對(Gτ,ρτ)上的相對羅巴算子,對于引理2中2),直接驗證可知

(11)

2 主要結果

設τ是李代數G上的擬跡函數,(G,ρ)是一個李表示對,T是李表示對(G,ρ)上的相對羅巴算子.令ρT:V→Gl(G)由式(5)給出.

先給出相對羅巴算子低階上同調群的一些結果.

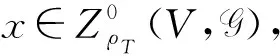
證明: 由式(8)直接計算可知,對任意的v∈V,有

對于1-階閉鏈,有如下包含關系.

1)τ(x)ω(y)=τ(y)ω(x);2)τ(x)ω([y,z])+τ(y)ω([z,x])+τ(z)ω([x,y])=0.

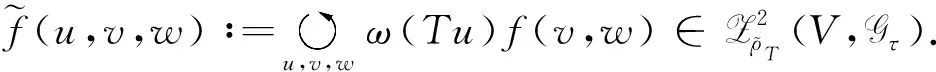
利用式(4),(11)以及ω滿足τ(x)ω(y)=τ(y)ω(x),直接計算可得

特別地,當線性函數ω:G→K取為擬跡函數τ時,有如下推論.

證明: 當線性函數ω:G→K為擬跡函數τ時,定理3中的條件1)自然成立,條件2)即是擬跡函數的定義,結論1)得證.

定理4存在一個鏈映射