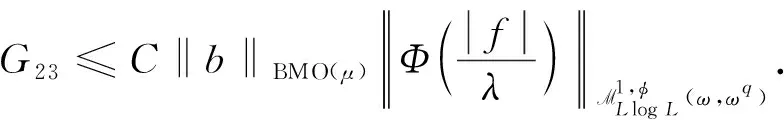RD空間上分?jǐn)?shù)次積分算子及其交換子在廣義Morrey空間的加權(quán)有界性
方光杰,陶雙平
(西北師范大學(xué) 數(shù)學(xué)與統(tǒng)計學(xué)院,蘭州 730070)
1 引言與主要結(jié)果
設(shè)(X,d,μ)為齊型空間[1-2],其測度μ滿足雙倍條件: 對任意的x∈X,存在常數(shù)C1∈(1,∞),使得
μ(B(x,2r))≤C1μ(B(x,r)),
(1)
其中B(x,r)={y∈X:d(x,y) μ(B(x,λr))≥C2μ(B(x,r)), (2) 關(guān)于RD空間的研究目前已有很多結(jié)果[4-9],例如: 文獻(xiàn)[4]引入了RD空間上的廣義加權(quán)Morrey空間;文獻(xiàn)[6]得到了RD空間上θ-型Calderón-Zygmund算子的BMO交換子在廣義加權(quán)Morrey空間中的有界性.本文主要考慮分?jǐn)?shù)次積分算子及其BMO交換子在RD空間上的廣義Morrey空間中的加權(quán)有界性,同時給出分?jǐn)?shù)次積分算子及其BMO交換子在該空間的端點估計. 對任意的球B?X,Muckenhoupt權(quán)類Ap(μ),A1(μ),A(p,q)(μ),A(1,q)(μ)分別由滿足下列條件的非負(fù)局部可積函數(shù)構(gòu)成[10]: 其中p′=p/(p-1)為p的對偶指標(biāo). 設(shè)1 (3) 且存在常數(shù)0<β<1,使得當(dāng)d(x,y)>2d(x,z)時,有 (4) (5) (6) 定義2[6]設(shè)1≤p<∞,φ: (0,∞)→(0,∞)為連續(xù)增函數(shù),給定非負(fù)可測函數(shù)ν,u∈X,廣義加權(quán)Morrey空間Mp,φ(ν,u)定義為 (7) 同理,對1≤p (8) (9) 往證當(dāng)條件(7)成立時,條件(8)和條件(9)也成立.條件(7)?條件(8)顯然成立,由于 則條件(7)?條件(9)也成立. 設(shè)ω∈A∞(μ),給定Young函數(shù)Φ和球B,則可測函數(shù)f在B上的加權(quán)平均Luxemburg范數(shù)定義[10]為 當(dāng)Φ(t)=t時,‖f‖Φ(ω),B=‖f‖L(ω),B;當(dāng)Φ(t)=t(1+log+t)時,‖f‖Φ(ω),B=‖f‖Llog L(ω),B.對ω∈A∞(μ)以及任意的球B?X,有如下廣義加權(quán)H?lder不等式[15]成立: (10) 設(shè)b∈BMO(μ),由加權(quán)John-Nirenberg不等式知,存在常數(shù)C>0,使得對任意的球B?X,有[6] ‖b-bB‖exp{L(ω)},B≤C‖b‖BMO(μ). (11) (12) 注意到當(dāng)t>0時,有t≤Φ(t)=t(1+log+t),且對任意的球B?X和ν∈A∞(μ),有 進(jìn)一步可得 (13) 本文主要結(jié)果如下: 定理1設(shè)0<α<1,1 定理2設(shè)0<α<1,p=1,1/q=1-α,ω∈A(1,q)(μ),若φ: (0,∞)→(0,∞)為連續(xù)遞增函數(shù),且滿足條件(8)和(9),則Iα從M1,φ(ω,ωq)到WMq,φq(ωq)有界. 定理3設(shè)0<α<1 ,1 本文C表示一個不依賴于主要參數(shù)的正常數(shù),在不同之處可表示不同值. 引理2[6]設(shè)(X,d,μ)為RD空間,若1≤p<∞,ω∈Ap(μ),則存在常數(shù)C5,C6>1,使得對任意的球B?X,有 ω(2B)≥C5ω(B), (14) ω(2B)≤C6ω(B). (15) 引理3設(shè)φ: (0,∞)→(0,∞)為連續(xù)遞增函數(shù)且滿足條件(9),則存在ε>0及充分小正數(shù)γ,使得 特別地,令p/q=1-γ,則對任意的0<η≤1,存在常數(shù)Cη>0,使得 證明: 利用文獻(xiàn)[6]中引理2.7的證明方法可得結(jié)論,故略. 引理4設(shè)(X,d,μ)為RD空間,若1≤p (16) 證明: 該引理的部分證明類似文獻(xiàn)[6]中引理2.9的證明.由于式(16)等價于 (17) 且φ滿足式(9),因此由引理3,只需證明 設(shè)bj=ωq(2jB),這里j∈,由式(8),(15),有 再由引理3,可得 引理5[6]若1≤p<∞,ω∈Ap(μ),b∈BMO(μ),則存在常數(shù)C>0,使得對任意的球B?X,j∈,有 |b2j+1B-bB|≤C(j+1)‖b‖BMO(μ), (18) (19) 引理6[10,16]設(shè)1 引理7[17]設(shè)(X,d,μ)為齊型空間,0<α<1,1 引理8[18]設(shè)(X,d,μ)為齊型空間,0<α<1,1 設(shè)B=B(x0,rB)={x∈X:d(x,x0) 首先估計D1.注意到ω∈A(p,q)(μ),由引理6可知ωq∈Aq(μ).利用式(8),(15)和引理7,得 其次估計D2.注意到當(dāng)x∈B,y∈(2B)c時,有d(x,y)~d(x0,y),V(x,y)~V(x0,y).由式(1),(3),(5),得 注意到ω∈A(p,q)(μ).利用A(p,q)(μ)條件、式(16)和H?lder不等式,有 結(jié)合D1和D2的估計并對所有的球B取上確界,即可得定理1的結(jié)論. 首先估計E1.注意到ω∈A(1,q)(μ),由引理6可知ωq∈A1(μ).利用式(8),(15)和引理7,得 其次估計E2.注意到ω∈A(1,q)(μ),由引理6可知ωq∈A1(μ)當(dāng)且僅當(dāng)ω∈A1(μ)∩RHq.利用式(16),(20)、Chebyshev不等式,A1(μ)條件和反H?lder不等式,有 結(jié)合E1和E2的估計并對所有的球B取上確界,即可得定理2的結(jié)論. 首先估計F1.注意到ω∈A(p,q)(μ),由引理6知,ωq∈Aq(μ).由引理8和式(8),(15),可得 其次估計F2.由交換子[b,Iα]的定義,對任意的x∈B,有 |[b,Iα](f2)(x)|≤|(b(x)-bB)||Iα(f2)(x)|+|Iα((bB-b)f2)(x)|. (21) 由式(20)的估計,同理可得 (22) 由式(20),(21),(22),得 注意到ω∈A(p,q)(μ),由引理6可知ωq∈Aq(μ).利用式(16),(18),(19)、H?lder不等式和A(p,q)(μ)條件,有 對于F23.設(shè)h(y)=ω(y)-p′,因為ω∈A(p,q)(μ),則由引理6可知h∈Ap′(μ).利用A(p,q)(μ)條件和式(19),得 利用式(16),(23)和H?lder不等式,得 綜合F1和F2的估計并對所有的球B取上確界,即可得定理3的結(jié)論. 首先估計G1.注意到ω∈A(1,q)(μ),由引理6可知ωq∈A1(μ).利用式(8),(12),(13),(15)和引理9,可得 其次估計G2.由式(20),(21),(22)和Chebyshev不等式,得 注意到當(dāng)t>0時,有t≤Φ(t).因為ω∈A(1,q)(μ),則由引理6可知ωq∈A1(μ)當(dāng)且僅當(dāng)ω∈A1(μ)∩RHq.利用式(18),(19)、反H?lder不等式和A1(μ)條件,可得 再利用式(12),(16)和反H?lder不等式,有 對于G23,因為ω∈A(1,q)(μ),故由引理6可知ω∈A1(μ).利用A1(μ)條件、廣義加權(quán)H?lder不等式和式(11),有 綜合G1和G2的估計并對所有的球B取上確界,即可得定理4的結(jié)論.
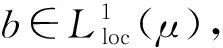






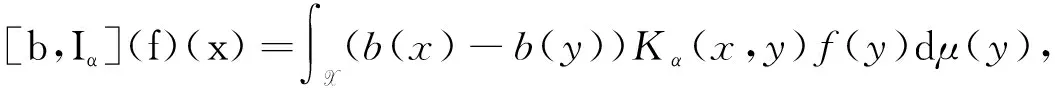







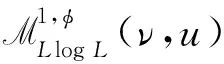




2 主要結(jié)果的證明




2.1 定理1的證明
2.2 定理2的證明

2.3 定理3的證明


2.4 定理4的證明