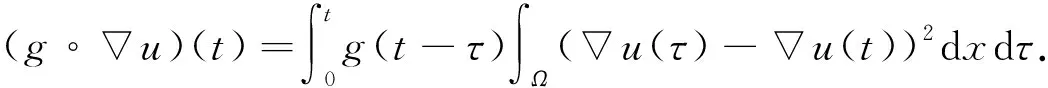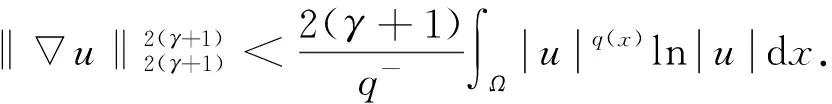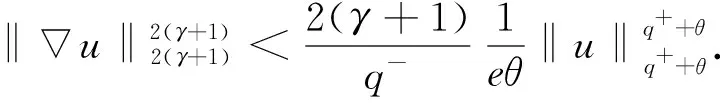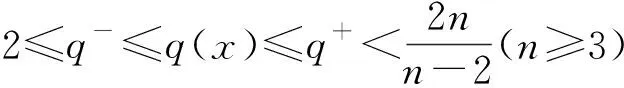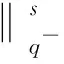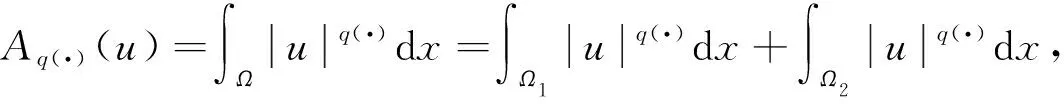具對數(shù)非線性項的Kirchhoff型黏彈性波動方程解的爆破性質(zhì)

武宇宇,高云柱

(北華大學 數(shù)學與統(tǒng)計學院,吉林 吉林 132013)

0 引 言

考慮如下具有變指數(shù)的對數(shù)非線性項的Kirchhoff型黏彈性波動方程:

(1)

其中Ω是n(n≥1)上具有光滑邊界?Ω的有界域.令M(s)=α+βsγ,α,β≥0,γ≥1.不失一般性,假設(shè)α=β=1.

設(shè)指數(shù)函數(shù)p(·)和q(·)是Ω上的可測函數(shù),且滿足

2≤p-≤p(x)≤p+

(2)

函數(shù)g(t)滿足如下條件:

(H2)g(τ)≥0,g′(τ)≤0且

近年來,具有變指數(shù)的偏微分方程受到廣泛關(guān)注,關(guān)于該類方程解的存在性、漸近性和爆破性研究已有很多結(jié)果[1-6].目前,具有對數(shù)非線性項的偏微分方程的研究也備受關(guān)注[7-8],而關(guān)于具有變指數(shù)的對數(shù)非線性項的相關(guān)研究結(jié)果相對較少[9].

本文記‖u‖L2(Ω)=‖u‖,‖u‖Lp(Ω)=‖u‖p.本文的C,c表示常數(shù),在不同之處可取不同值.

1 預備知識

設(shè)p:Ω→[1,∞)是一個可測函數(shù),Ω是n上的有界域,則變指數(shù)Lebesgue空間Lp(x)(Ω)定義為

給空間Lp(x)(Ω)賦予Luxemburg范數(shù)

這里Lp(x)(Ω)是一個Banach空間.變指數(shù)Sobolev空間W1,p(x)(Ω)定義為

W1,p(x)(Ω)={u∈Lp(x)(Ω):u存在且|u|∈Lp(x)(Ω)}.

易知,變指數(shù)Sobolev空間也是一個Banach空間,且有如下范數(shù):

‖u‖1,p(x)=‖u‖p(x)+‖u‖p(x).

(3)

這里A>0,0<δ<1.

引理1[10]設(shè)Ω是n上的有界域,p(·)滿足Log-H?lder連續(xù)條件,則對任意的有‖u‖p(·)≤C‖u‖p(·),其中C=C(p-,p+,|Ω|)>0.

引理3[7]對任意的θ>0,有

類似文獻[2,6],易得如下問題(1)弱解的存在性定理:

2 主要結(jié)果

引理4假設(shè)條件(H1),(H2)和式(2),(3)成立,則

是一個非增函數(shù),且

證明: 將式(1)乘ut,并在Ω上積分可得

估計式(5)等號左端最后一項,有

將式(6)代入(5)得

‖u‖2(γ+1)

證明: 由E(0)<0和式(4)可得

這里Ω1={x∈Ω: |u|<1},Ω2={x∈Ω: |u|≥1}.故

(10)

(11)

‖u‖2(γ+1)

證明: 1)和2)的證明過程可參見文獻[6].下面證明3)～5).

由H(t)的定義和條件(H1),可得

將式(12)代入1)可得

因此,3)得證.4)是3)的特殊情形.

(13)

(14)

令H(t)=-E(t),由式(7)可知,H(t)>0.由H(t)的定義和式(9),可知

(15)

由式(11)和引理5,可得

結(jié)合式(15)和式(16),有

(17)

所以

(18)

結(jié)合式(14)和式(18)可得

其中

(a+b)p≤2p-1(ap+bp).

(19)

當Aq(·)(u)≥1時,有

當Aq(·)(u)<1時,有

因此結(jié)論得證.

證明: 結(jié)合引理6中5)和式(17),可得

(20)

將Ψ(t)定義為

(21)

其中ε充分小,且

(22)

對式(21)求導可得

將式(1)乘u并在Ω上積分,可得

所以

由Cauchy-Schwarz不等式和Young’s不等式,得

(24)

將式(24)代入式(23),有

將等式H(t)兩邊同乘(-εq-(1-ξ)),得

這里0<ξ<1.在式(25)的不等號右邊同時加、減式(26),得

當ξ充分小時,可得

這里

若存在X,Y≥0,η>0,l′,l∈+,滿足條件則Young’s不等式成立.因此,可得

(29)

這里η是一個與時間t有關(guān)的常數(shù).將式(29)代入(28)得

選取η,使其滿足η-p(x)/(p(x)-1)=kH-σ(t),其中k>0充分大.則

利用引理6中5)和式(20),通過簡單計算可得

由引理6和式(22),有

或者

結(jié)合引理6中1)可得

(33)

將式(33)代入式(31),得

因此,結(jié)合引理6中5)和式(34)可得

另一方面,由H?lder不等式得

由Young’s不等式,有

(36)

這里s=2/(1-2σ)≤q-.利用引理6中4)可得

結(jié)合式(19)和式(21)可得

由式(35)和式(37)可得

Ψ′(t)≥ζΨ1/(1-σ)(t),

(38)