具有Allee效應(yīng)的不確定Logistic種群模型
高采文,張志強,劉寶亮
(山西大同大學 數(shù)學與統(tǒng)計學院,山西 大同 037009)
Allee[1]對生物種群的研究表明,群體生存有利于生物種群的存活、繁殖、抵御外敵,但過于密集或過于稀疏都會對繁殖產(chǎn)生負面影響,阻礙種群的發(fā)展,這就是Allee效應(yīng).具有Allee效應(yīng)的種群有自身的最佳密度,當密度低于一定閾值時,種群將會滅絕.Allee效應(yīng)的強弱影響生物種群的生殖狀態(tài)、進化方向以及生存狀態(tài).描述Allee效應(yīng)的數(shù)學模型目前已有很多,其中以確定性模型和隨機模型為主.確定性模型對種群數(shù)量增長的描述較籠統(tǒng),忽略了其他內(nèi)外因素隨時間波動對系統(tǒng)行為的影響,很難精準預(yù)測種群的變化趨勢.隨機模型盡管在實踐中應(yīng)用廣泛,但應(yīng)用隨機模型的前提是事件的概率分布函數(shù)充分接近實際頻率,即滿足大數(shù)定律.但由于各種原因,實踐中有時無法獲得樣本數(shù)據(jù),只能依靠領(lǐng)域?qū)<夜烙嬍录l(fā)生的可能性并給出其信度.此外,由于Wiener過程的性質(zhì),隨機微分方程在描述許多時變系統(tǒng)時存在不一致的現(xiàn)象[2].因此,為更好地描述生物種群動態(tài)過程中的各種噪聲需考慮新方法.
Liu[3]提出了不確定性理論,用于解決隨機模型中的悖論.為描述隨時間變化的不確定現(xiàn)象,Liu[4]引入了不確定過程的概念,Liu過程即為一種不確定過程,它是平穩(wěn)獨立的增量過程,具有連續(xù)的Lipschitz樣本路徑.與Wiener過程驅(qū)動的隨機微分方程不同,不確定微分方程由不確定過程驅(qū)動.目前,不確定微分方程已成為處理動態(tài)不確定系統(tǒng)的主要工具.不確定理論廣泛應(yīng)用于不確定規(guī)劃、不確定可靠性分析和不確定金融等領(lǐng)域.
考慮到種群系統(tǒng)不可避免地受自然界中各種不確定噪聲的影響,本文在具有Allee效應(yīng)的確定性種群模型基礎(chǔ)上進一步考慮不確定噪聲的影響,提出用不確定微分方程描述具有Allee效應(yīng)的不確定Logistic種群模型.該模型將噪聲項視為一個不確定變量,其期望值為0、方差為1.本文提出的模型為研究具有Allee效應(yīng)的種群動態(tài)行為提供了一種新方法.
1 預(yù)備知識
定義1[3]設(shè)Γ是一個非空集合,L是Γ上的σ代數(shù).不確定測度M是從L到[0,1]的函數(shù),滿足下列條件:
1)(規(guī)范性公理) 對全集Γ,有M{Γ}=1;
2)(對偶性公理) 對任意事件Λ,有M{Λ}+M{Λc}=1;

4)(乘積測度公理) 令(Γk,Lk,Mk)(k=1,2,…)是不確定空間,乘積不確定測度M滿足
其中Λk是Lk中的任意事件,k=1,2,….
定義2[5]如果不確定過程Ct滿足下列條件,則Ct稱為一個Liu過程:
1)C0=0,幾乎所有的樣本軌道Lipschitz連續(xù);
2)Ct具有平穩(wěn)獨立增量;
3) 每個增量Cs+t-Cs是一個期望值為0、方差為t2的正態(tài)不確定變量.



Liu等[8]證明了ξ=f(ξ1,ξ2,…,ξn)的期望值為


2 模型的建立
種群的數(shù)量通常以指數(shù)方式增長,連續(xù)的Malthus種群模型為

(1)
其中Nt表示t時刻種群的數(shù)量,r為種群的內(nèi)稟增長率.
種內(nèi)競爭是生物界普遍存在的現(xiàn)象,例如,雄蝗蟲為爭搶雌蝗蟲的角逐及雌蝗蟲為爭搶產(chǎn)卵場所而進行的斗爭,都會影響它們的生物潛能,并最終導致種群數(shù)量下降.考慮到密度限制和擁擠效應(yīng),在模型(1)上增加一個密度制約因子(1-Nt/K),即可得Logistic種群模型:

(2)
其中K為環(huán)境容納量.當Nt
為生存、繁衍并抵御外敵入侵,生物個體之間也需要相互合作.例如: 螞蟻作為一個團隊,可以把質(zhì)量是自己數(shù)十倍的物體搬回巢穴;食草動物的聚集可減少外敵入侵.這種生物個體間的合作會增加種群的繁殖成功率或存活率,從而增加種群的規(guī)模或密度,這些均可視為Allee效應(yīng).對具有Allee效應(yīng)的種群,在模型(2)上增加因子(1-K0/Nt),即可得具有Allee效應(yīng)的Logistic種群模型:

(3)
其中K0
不確定擾動在自然界普遍存在.模型(3)是確定性模型,忽略了噪聲項,引入不確定擾動項則更符合實際.一種引入的方法是假設(shè)不確定噪聲項主要擾動內(nèi)稟增長率,即

(4)
其中:Ct為Liu過程;σ為定義在[0,+∞)上的實數(shù),表示噪聲的強度.因此可得具有Allee效應(yīng)的不確定Logistic種群模型:

(5)
其中噪聲項dCt/dt為正態(tài)不確定變量,期望為0、方差為1.模型(5)不僅考慮了Allee效應(yīng)帶來的動態(tài)影響,而且考慮了實際應(yīng)用中不能忽略的不確定擾動,因此,模型更合理.下面討論具有Allee效應(yīng)的不確定Logistic種群模型的解及解的α軌道.
3 模型的解
定理1具有Allee效應(yīng)的不確定Logistic種群模型有解
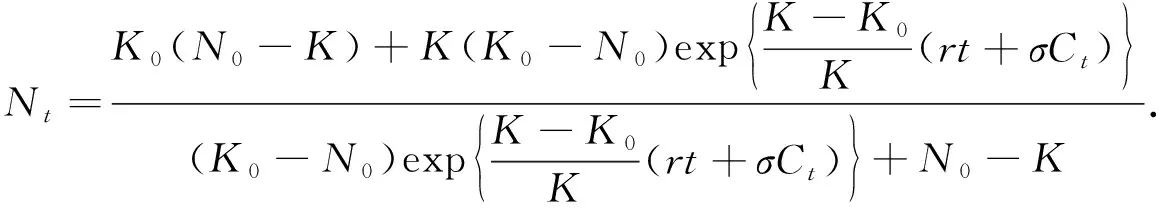
(6)

(7)
對式(7)兩邊從0到t求積分,得
即
從而

(8)
求解式(8)可得式(6).因此,具有Allee效應(yīng)的不確定Logistic種群模型的解完全由參數(shù)r,σ,K,K0和初值N0確定.
定理2若具有Allee效應(yīng)的不確定Logistic種群模型給定初值N0>0,則有α軌道

(9)

證明: 由定義3可知,具有Allee效應(yīng)的不確定Logistic種群模型解的α軌道滿足相應(yīng)常微分方程

(10)
對式(10)兩邊求積分可得式(9),因此結(jié)論得證.
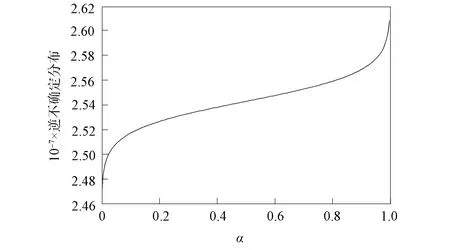
定理3對具有Allee效應(yīng)的不確定Logistic種群模型,當K0 當K0 證明: 考慮函數(shù) 分析表明: 當K0 定理4對于具有Allee效應(yīng)的不確定Logistic模型,當t→∞時,有 (11) 證明: 由式(8),有 整理得 從而 由于 因此可得結(jié)論.表明環(huán)境容納量K是一個平衡狀態(tài),在式(11)的意義下穩(wěn)定. 目前,關(guān)于不確定微分方程的參數(shù)估計問題已得到廣泛關(guān)注.Yao等[10]提出了一種基于不確定微分方程差分形式的矩估計法.對于矩估計法無解的情形,研究者們又提出了廣義矩估計法,將問題轉(zhuǎn)化為求目標函數(shù)最小化的最優(yōu)解.此外,Sheng等[11]用最小二乘估計法估計未知參數(shù);Lio等[12]討論了用不確定極大似然估計法估計不確定回歸模型中的未知參數(shù);Liu等[13]研究了基于不確定極大似然估計的不確定微分方程參數(shù)估計方法.本文利用廣義矩估計法對具有Allee效應(yīng)的不確定Logistic種群模型中的參數(shù)r和σ進行估計. 具有Allee效應(yīng)的不確定Logistic種群模型的Euler差分形式為 整理得 (12) 由式(12),有 (13) 模型的解Nt在時刻t1 (14) k階總體矩為 由于標準正態(tài)不確定分布的期望為0、方差為1,所以目標函數(shù)最小值為 (15) 根據(jù)廣義矩估計法知,式(15)的最優(yōu)解是未知參數(shù)r和σ的廣義矩估計值.所以,未知參數(shù)r和σ的廣義矩估計值等價于求下列方程組: (16) 求解方程組(16),可得r和σ的估計值分別為 (17) 下面對具有Allee效應(yīng)的不確定Logistic人口模型做參數(shù)估計,并研究模型解的性質(zhì).表1列出了美國1790年到1990年的人口統(tǒng)計數(shù)據(jù).根據(jù)文獻[14],模型中參數(shù)K=265×106,N0=3.9×106,同時假設(shè)K0=10. 表1 1790年到1990年美國人口統(tǒng)計數(shù)據(jù) 根據(jù)1790年到1990年美國人口的統(tǒng)計數(shù)據(jù),由式(14)可得標準正態(tài)分布的21個樣本: 目標函數(shù)最小值為 (18) 根據(jù)式(17)可知式(18)的最優(yōu)解,即未知參數(shù)r和σ的廣義矩估計分別為 (19) (20) 將樣本觀測值Nti+1(i=1,2,…,21)代入式(19)和式(20),解得 (21) 從而得到具有Allee效應(yīng)的不確定性Logistic人口模型: (22) 將式(21)代入式(18),計算可得目標函數(shù)的最小值為0.151 1×10-6,接近于0. 下面驗證估計值的合理性.對任意給定的α,β∈(0,1)且α>β,在時刻t0,因為 所以 在實際應(yīng)用中,為維持社會穩(wěn)定或生態(tài)平衡,當人口數(shù)量接近極值時,政府需要制定相應(yīng)政策限制人口數(shù)量的自然增長或減少,從而防止極端現(xiàn)象.下面討論具有Allee效應(yīng)的不確定Logistic人口模型解的極值及解的積分不確定分布. 假設(shè)具有Allee效應(yīng)的不確定性Logistic人口模型(22)中,N0=3.9×106,則模型的解為 解的α軌道為 圖1 Nt的觀測值和α軌道Fig.1 Observations and α-paths of Nt 圖2 Nt的α軌道Fig.2 α-paths of Nt 如圖4所示. 圖3 Nt極值的逆不確定分布Fig.3 Inverse uncertainty distributions of extreme values of Nt 圖4 Nt積分的逆不確定分布Fig.4 Inverse uncertainty distributions of integral of Nt 綜上所述,考慮到不確定噪聲的影響,本文提出了用不確定微分方程描述的具有Allee效應(yīng)的不確定Logistic種群模型.該模型的特點是將Allee效應(yīng)與不確定擾動相結(jié)合.首先,給出了具有Allee效應(yīng)的不確定Logistic種群模型的解及解的α軌道,并利用不確定分析方法討論了解的期望值和平衡態(tài)的穩(wěn)定性;其次,討論了模型的參數(shù)估計;最后,通過數(shù)值實例對模型的參數(shù)估計及解的極值與積分的逆不確定分布進行了說明.
4 模型的參數(shù)估計
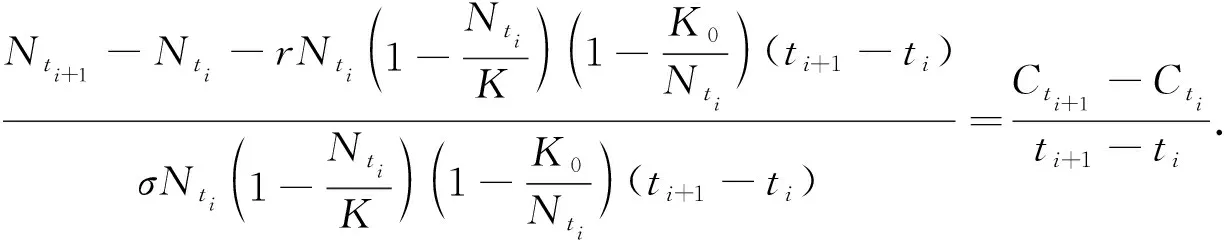
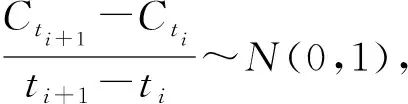




5 實例分析

5.1 具有Allee效應(yīng)的不確定Logistic人口模型的參數(shù)估計




5.2 具有Allee效應(yīng)的不確定Logistic人口模型解的極值和積分