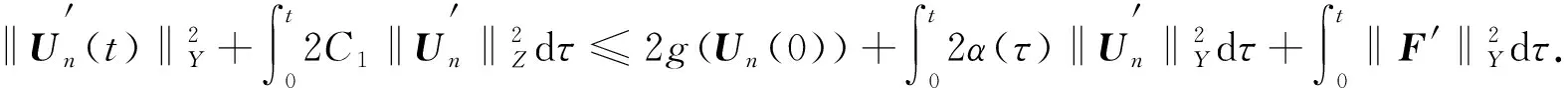二維不可壓縮磁-微極流初邊值問題的全局解
吳辰龍,劉瑞寬
(西南石油大學 理學院,成都 610500)
0 引 言
考慮如下二維不可壓縮磁-微極流體動力學方程組:

(1)
其中:Ω?2為邊界光滑的有界開區域;u(t,x)∈2,w(t,x)∈2,b(t,x)∈2和p(t,x)∈分別表示流速、微旋轉速度、磁場強度和靜水壓力;f(t,x),g(t,x)∈2為已知的外力函數.本文考慮如下的齊次邊界條件和初始條件:

(2)
u(0,x)=u0(x),w(0,x)=w0(x),b(0,x)=b0(x),x∈Ω,
(3)

磁-微極流方程常被用于描述具有微旋轉效應的導電流體(如等離子體、液態金屬)在磁場作用下的流動現象,對太陽或地球磁場的起源、超新星爆發、受控熱核反應等研究具有重要意義,目前已得到廣泛關注[1-8].例如,Rojas-Medar等[2-3]利用Galerkin方法討論了方程組(1)在無滑移型邊界條件下的全局弱解與局部強解,并解決了二維情形下弱解的唯一性問題;Ortega-Torres等[4]在小初值的前提下得到了全局強解的存在性;Yuan[5]獲得了方程組(1)光滑解的一個爆破準則;Xu[6]通過Fourier局部化方法改進了三維磁-微極流問題一些已知的弱解正則性結果;Zhang等[7]在Tribel空間中建立了僅用速度場梯度控制的弱解的正則性準則.馬天[9]建立了T-弱連續算子方法,該方法可有效解決一些非線性偏微分方程全局解的適定性問題;基于T-弱連續算子方法,馬天等[10]討論了一類二階非線性拋物方程初邊值問題全局強解的存在性與正則性;Zhang等[11]得到了一類描述多元體相分離現象的四階擬線性演化方程的整體弱解的存在性結果;Wang等[12]獲得了二維不可壓縮Marangoni問題整體弱解的存在性與唯一性定理;Wu[13]證明了一類完全非線性發展方程強解的整體存在性.受上述研究啟發,本文利用T-弱連續算子方法研究二維不可壓縮磁-微極流初邊值問題(1)-(3)全局解的存在性與唯一性.
1 預備知識
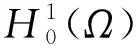

其中1≤p≤∞.
類似文獻[14],定義如下函數空間:
并始終假設:

Y=U1×V1×W1,H=U2×V2×W2,Z=U3×V3×W3.
注意到L2(Ω,2)可進行形如L2(Ω,2)=U1⊕的Leray分解,這里

下面用P表示從L2(Ω,2)到U1的正交投影算子,即P是Leray投影算子.本文始終假設U=(u,w,b),F=(f,g,0),并定義算子G:H×(0,∞)→Y*為

(4)
這里Y*是Y的對偶空間.于是,初邊值問題(1)-(3)可等價為如下形式:

(5)


成立,則U稱為問題(5)的一個全局弱解.
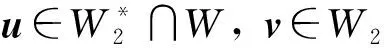
定義2[9]若對任意的xn∈W1,xn?x0,且有子列{xnk}∈W1滿足






則在L2((0,T)×Ω)上對任意的|α|≤m-1,有Dαun→Dαu0.
2 主要引理與估計
下面總假設?i=?/?xi,并約定出現指標i,j時,表示從1到2求和;出現指標k時,表示對1~3求和.為方便,記u=(u1,u2),w=(w1,w2),b=(b1,b2),u1,j=uj,u2,j=wj,u3,j=bj,j=1,2.
引理2若G為式(4)中定義的算子,則有如下不等式成立:
這里常數C>0.
證明: 對式(4)乘以U,并在Ω上積分可得
利用分部積分公式并結合divu=0,有
再注意到
則有
這里常數C>0.
引理3對任意的0 其中常數C>0. 證明: 定義算子 (6) 則對?S∈Y,由分部積分公式有 注意到U∈L2((0,T),H)∩L∞((0,T),Y),S∈E,則 進一步,有 綜合上述不等式,即有 引理4若G為式(4)中定義的算子,則G是T-弱連續的. 證明: 取L2((0,T),Z)中有界序列{Un}且Un?U0,則由引理1知,{Un}在L2((0,T),Y)中強收斂,即 Un→U0(L2((0,T),Y)), (7) 其中0 對?S∈E,顯然有 其中B為式(6)中定義的算子. 由分部積分公式,并結合式(7),(8)可得 同時有 從而 (13) 于是由式(9)~(13)可得 引理5若U=(u,w,b),S=(s1,s2,s3),則對任意的U∈H,S∈E, 成立,對任意的U,S∈E, 證明: 令U=(u,w,b),S=(s1,s2,s3),B為式(6)定義的算子,結合H?lder,ε-Young和Poincaré不等式及分部積分公式,可得 顯然,泛函g:H→[0,∞)是有界的. 又對任意的U,S∈E,有 利用H?lder和ε-Young不等式,有 取X0=Y,X1/2=Z,則有如下插值不等式[15]: (15) (16) 這里X1/4=W1/2,2(Ω,2)×W1/2,2(Ω,2)×W1/2,2(Ω,2).利用分數階Sobolev嵌入定理[15],有 (17) (18) 從而結合式(14)~(18),有 定理1令U0=U(0)=(u0,w0,b0),F=(f,g,0),且F(0,x)=0,則如下結論成立: 1) 對任意的U0∈Y,F∈L2((0,T),Y)和0 2) 對任意的U0∈H,F∈W1,2((0,T),Y)和0 記Yn=span{e1,…,en}.對方程(5)利用標準的Galerkin技術,并考慮如下常微分方程組: (19) (20) 在式(20)中令S=Un,則有 (21) 結合引理2與式(21),可得 利用Gronwall不等式,對任意的0 (23) 由式(22)顯然可得 再結合式(23),可推出 (24) 從而由式(23)與式(24)可知 {Un}?L∞((0,T),Y)∩L2((0,T),Z), (25) 由引理3和式(19)可知 (26) (27) 由引理4知,算子G是T-弱連續的,因此對任意的S∈Yn,有 (28) 2) 由算子G的Fréchet可微性,并結合式(19),易見Un滿足 (29) 由引理5可知 (30) 對任意的S∈Yn,有 (31) (32) 結合式(30)與式(32),有 (33) 由于E?H,U0∈H,因此在H中有Un(0)→U0.又由式(28)知α(τ)∈L1(0,T),則對式(33)應用Gronwall不等式,可得 利用中值公式,有 (34)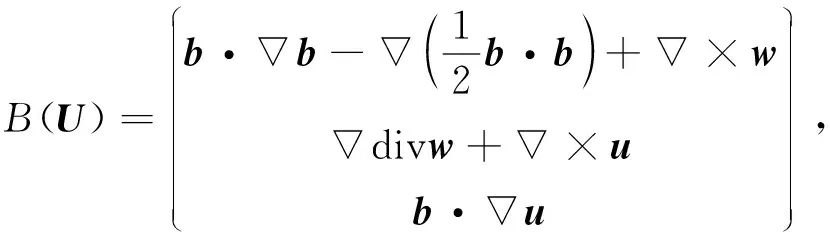

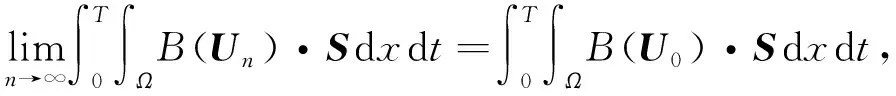





3 主要結果及其證明