螺旋纏繞復合材料圓柱殼屈曲特性

左新龍，張 建，唐文獻，李永勝，展 銘

(1.江蘇開放大學 信息工程學院，江蘇 南京 210000；2.江蘇科技大學 船舶與海洋工程工程學院，江蘇 鎮江 212003；3.中國船舶科學研究中心，江蘇 無錫 214082)

0 引 言

潛水器是人類探索海洋、開發海洋資源必不可少的基礎裝備，耐壓殼作為潛水器的核心部件，其結構形式及材料的選擇直接影響到潛水器的有效載荷[1]。圓柱形耐壓殼（下文簡稱圓柱殼）是最常用結構形式之一[2]，而復合材料圓柱殼具有良好的比強度、比剛度、抗疲勞、耐腐蝕和承載能力等，在潛水器、水下滑翔機等裝備的耐壓結構件上得到廣泛應用[3–4]。

復合材料圓柱殼制備可采用卷制與纏繞2 種工藝。圓柱殼纖維纏繞主要分單一螺旋纏繞、螺旋加環/縱向纏繞。國內外學者對靜水壓下卷制及纏繞2 種工藝制備的碳纖維復合材料圓柱殼屈曲特性，進行了一系列的理論、數值與試驗研究。卷制工藝制備的圓柱殼，其纖維層依次疊層、規律鋪設，力學性能研究比較成熟。Perry[5]、ASME[6]、NASA[7]和Shen[8]等基于層合板理論，分別給出了復合材料圓柱殼的臨界屈曲載荷理論求解公式。Messager[9–10]基于三階剪切變形理論，提出了缺陷下的圓柱殼屈曲理論模型，并與有限元模型、試驗進行驗證。潘光等[11–16]建立了圓柱殼層合板失效數學模型，優化了碳纖維層鋪設角度及鋪層數，并試驗研究了碳纖維復合材料圓柱殼的最終破壞模式和失效載荷。

復合材料圓柱殼纏繞工藝是以一定帶寬的纖維不間斷螺旋纏繞，可形成類似編織形殼體，在圓柱殼內外表面均有螺旋纖維帶，起到螺旋加強作用，其承載能力要高于卷制工藝。Moon 等[17]對靜水壓下螺旋加環型纖維纏繞復合材料中厚殼的屈曲特性及失效模式進行了數值和試驗研究，分析了螺旋纏繞角變化與環向纏繞層比例對屈曲臨界載荷和失效模式的影響。Schillo 等[18]設計了螺旋纏繞角為±30°的薄圓柱殼結構，試驗研究了圓柱殼軸向載荷下屈曲失穩模式。李卓禹等[19]基于蔡-吳強度理論、哈森理論和第四強度理論，建立了靜水壓下纖維纏繞復合材料圓柱殼的有限元模型，給出了纖維纏繞層和芯材的強度失效判據。然而，上述研究沒有考慮材料剛度退化對圓柱殼承載載荷及失效模式的影響，且針對螺旋纏繞工藝下的復合材料圓柱殼實際破壞過程未進行闡明。

為此，本文開展單一螺旋纏繞復合材料圓柱殼屈曲特性試驗與數值研究。首先制作不同長徑比（圓柱殼有效長度與內徑的比值）的單一螺旋纏繞復合材料圓柱殼，并對其制作誤差檢測，試驗研究靜水壓下圓柱殼的失效模式。其次，基于Hashin 強度準則及漸進損傷理論，建立復合材料圓柱殼等效有限元模型，并根據NASA SP-8 007[7]規范和Shen[8]理論公式，分別求解復合材料圓柱殼屈曲載荷，分析討論不同長徑比對復合材料圓柱殼屈曲特性的影響規律，比較分析理論模型、有限元模型和靜水壓力試驗結果。研究成果對單一螺旋纏繞復合材料圓柱殼承載載荷和失效模式分析具有指導意義。

1 試驗材料與方法

1.1 圓柱殼制作

采用樹脂基碳纖維預浸帶（UD600-SGL50K：層厚0.13 mm；樹脂陶氏760E/766H），不間斷濕纏繞工藝制作長1 m 復合材料圓柱殼，纏繞張力為50 N。考慮圓柱殼受均勻外壓下最佳纖維纏繞角區間[20]，本文制作圓柱殼螺旋纏繞角度選用[±55°]14。纏繞鋪層與分段切割方式如圖1 所示。

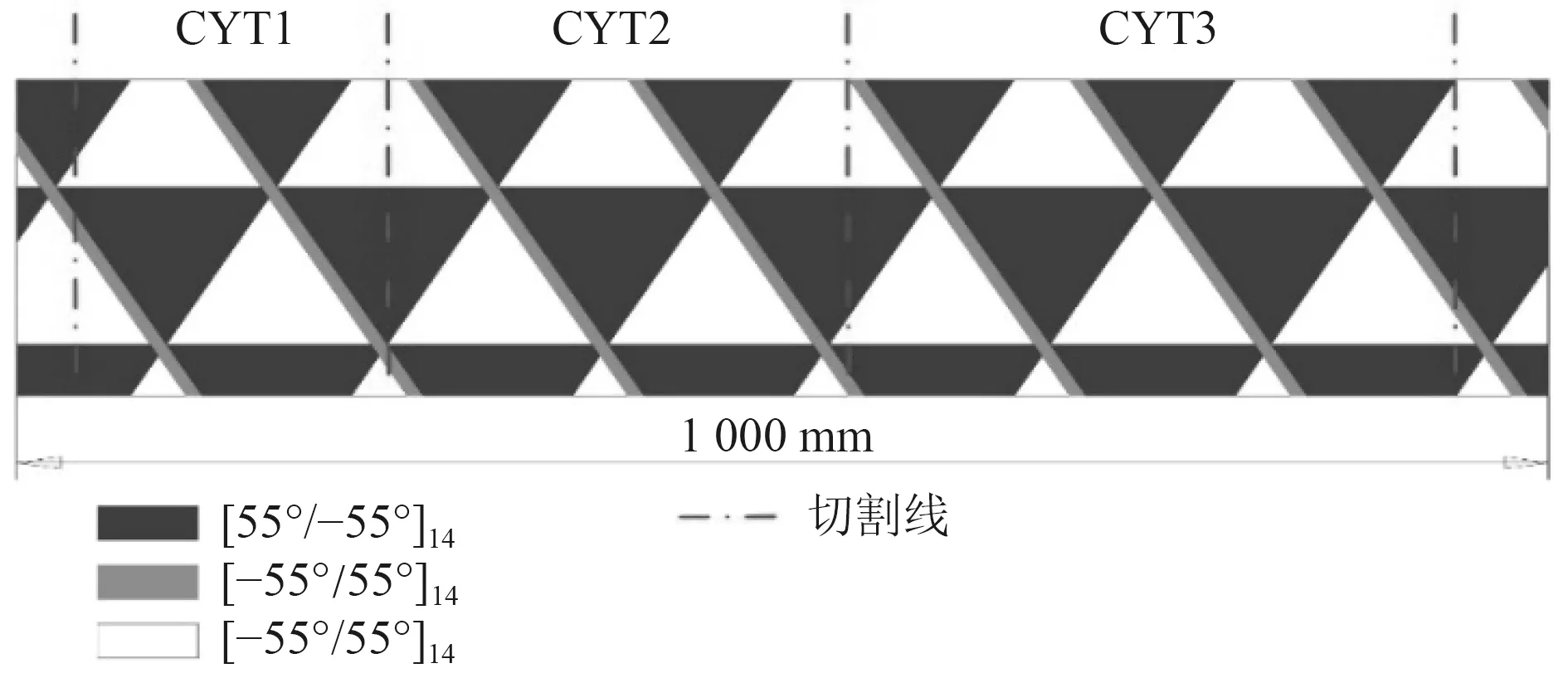
圖1 CYT 柱殼纏繞鋪層示意Fig.1 Layup patterns of cylinders CYT

長1 m 復合材料圓柱殼分割成3 段，依次為CYT1、CYT2 和CYT3（見圖1），其名義長度分別為195 mm、295 mm 和405 mm（見表1）。設計用于靜水外壓試驗的復合材料圓柱殼結構，如圖2 所示。復合材料圓柱殼兩端采用304 不銹鋼封蓋密封，主要參數為圓柱殼有效長度L、圓柱殼內徑d、圓柱殼壁厚t、不銹鋼封蓋外徑D=225 mm、不銹鋼封蓋厚度b=20 mm、不銹鋼封蓋凹槽深度h=15 mm。

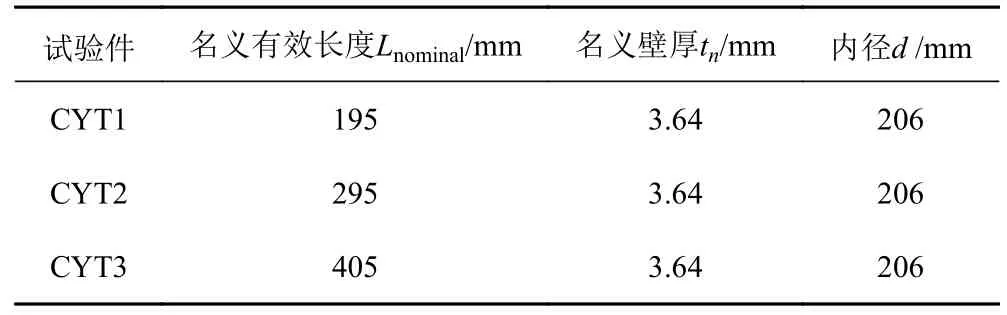
表1 圓柱殼試驗件幾何參數Tab.1 Geometric parameters of the composite cylinder

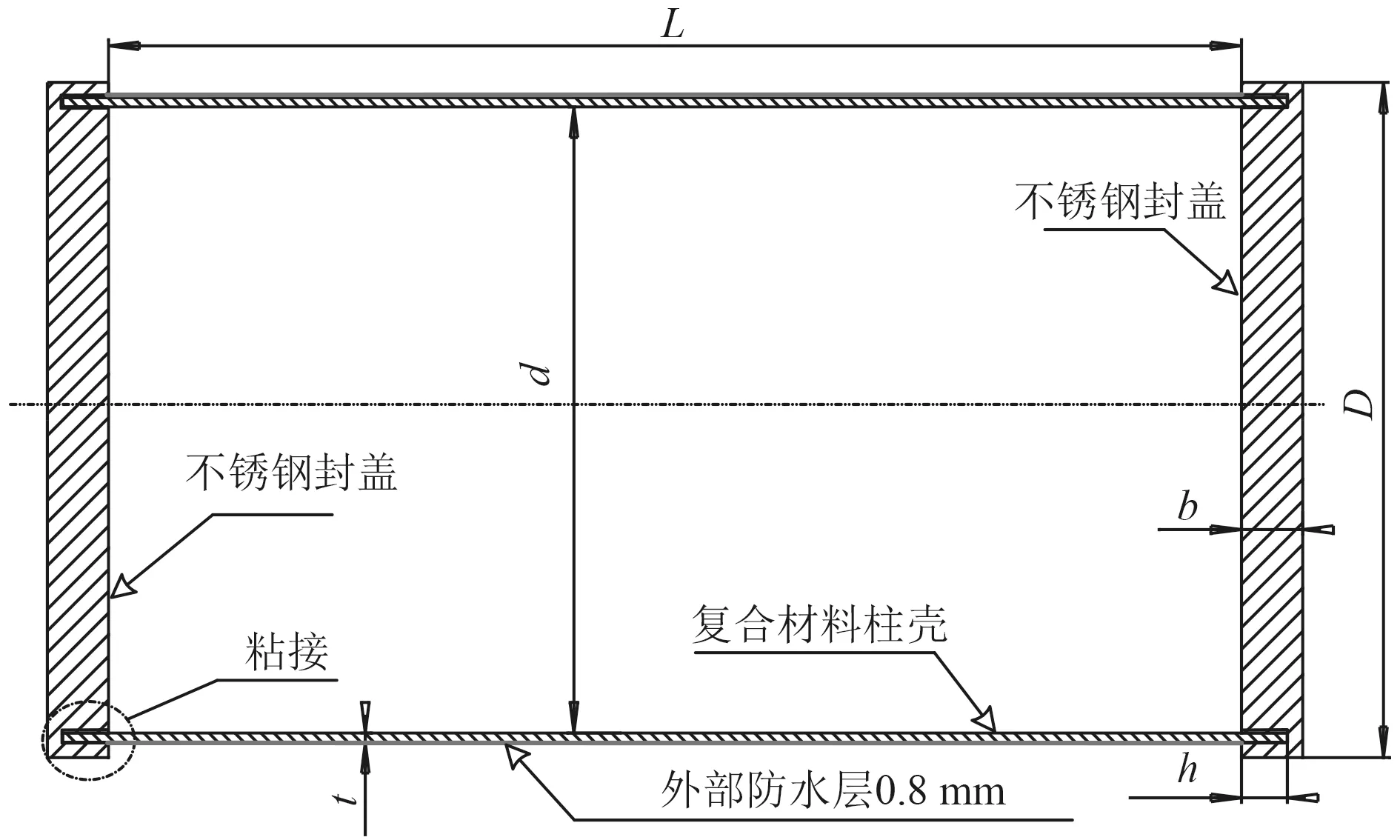
圖2 復合材料柱殼與不銹鋼封蓋相連示意Fig.2 Joining concept of composite cylinder and steel flanges

復合材料圓柱殼與封蓋使用Araldite 2015 環氧樹脂膠粘接固定。為避免圓柱殼外壓試驗時表面滲水，其外表面涂敷3 層GDJN001 聚脲防水涂料，總厚度約0.25 mm。復合材料圓柱殼試驗件如圖3 所示，設計尺寸參數如表1 所示，碳纖維層合板的材料屬性如表2所示。304 不銹鋼封蓋彈性模量為190 GPa，泊松比為0.31。

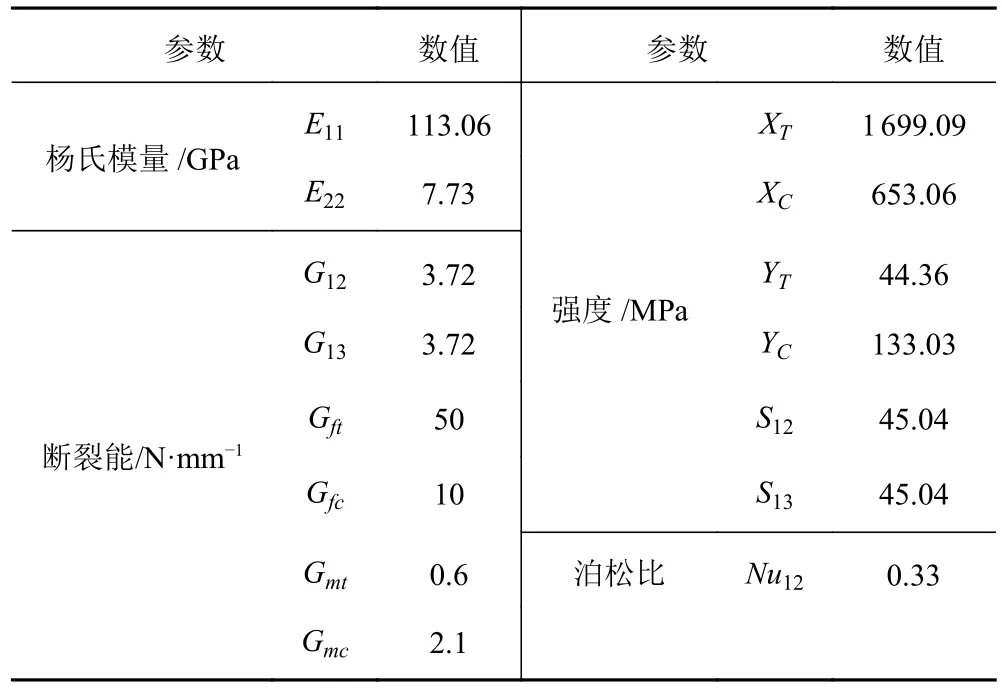
表2 復合材料層合板材料屬性Tab.2 Material properties of composite provided by the manufacturer

圖3 復合材料柱殼試驗件Fig.3 Composite cylinder specimens

1.2 制作誤差檢測

選用Open Technologies 3D 掃描儀（單筆掃描范圍150 mm×115 mm×150 mm；掃描儀像素200 M；精度0.02 mm），針對已制作的CYT1、CYT2 和CYT3 復合材料圓柱殼，規范操作，獲得其外表面三維輪廓。采用GOM INSPECT 三維檢測軟件，檢測試驗件與名義圓柱殼輪廓的誤差分布。分析結果如圖4所示，圖標為試驗件與名義外輪廓基于曲率半徑的誤差及誤差頻率。CYT1 柱殼與名義外輪廓最大曲率半徑誤差為0.73 mm，誤差為0.2～0.6 mm，占總誤差段的80%以上，最大誤差主要為柱殼最外層55°纏繞層。CYT2 最大曲率半徑誤差為0.78 mm，誤差主要分布在0.4 mm。CYT3 最大誤差為0.83 mm，誤差主要分布在0.2～0.6 mm。此外，Schilo[18]制作的纏繞編織復合材料圓柱殼（設計壁厚0.81 mm），最大誤差0.45 mm，誤差主要分布在0.24 mm 左右。考慮三維掃描設備精度0.02 mm，后處理曲面造型及軟件系統誤差，制作的復合材料柱殼制作誤差屬于纏繞工藝合理誤差范圍，可用于靜水壓力試驗研究。

圖4 CYT 柱殼外表面與名義柱殼誤差分布Fig.4 Deviations of the external surfaces of CYT cylinders from their perfect geometries

針對CYT1、CYT2 和CYT3 復合材料圓柱殼，沿周向15°間隔劃分壁厚測量參考線，參考線軸向方向間隔10 mm 截取參考點，采用定制千分尺（精度0.01 mm）進行壁厚測量。如圖5 所示，CYT1、CYT2 和CYT3總測點分別為24×20 個、24×30 個、24×40 個。因千分尺測量限制，CYT2 中部24×7 個及CY3 中部24×17 個參考點未進行測量，考慮CYT1、CYT2 和CYT3 為圓柱殼整體纏繞后切割分段，未測量區域不影響壁厚統計分析。各試驗件壁厚統計如表3 所示。CYT1、CYT2和CYT3 實測平均壁厚分別為3.755 mm、3.808 mm 和3.807 mm，平均壁厚最大值與最小值相差誤差Δ=0.053 mm，整體平均壁厚為toav=3.79 mm，Δ/toav僅為0.001 4。因此，復合材料圓柱殼試驗件壁厚均勻性較好。CYT1、CYT2 和CYT3 圓柱殼壁厚，相較于名義厚度tn=3.64 mm，分別高3.16%、4.62%和4.59%，主要由于預浸料自身誤差、樹脂加熱后厚度變化、纏繞殘留氣泡、纖維錯位等因素。

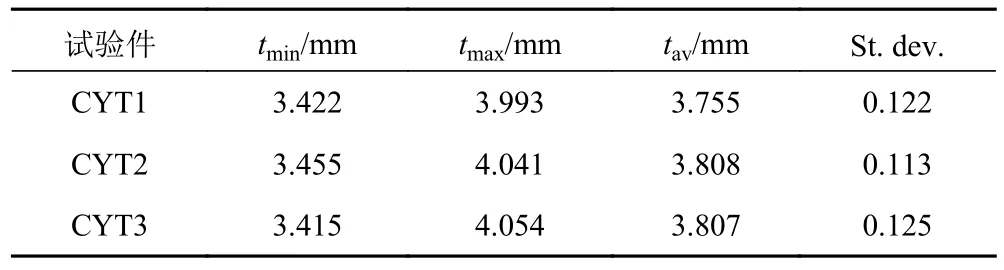
表3 復合材料試驗件壁厚Tab.3 Wall thickness of cylinders

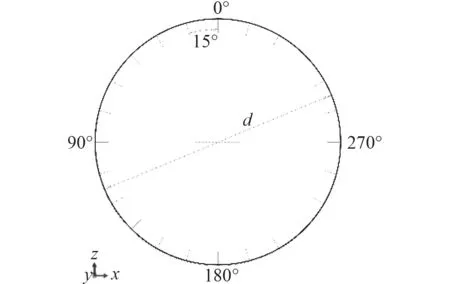
圖5 柱殼測厚點周向分布示意圖Fig.5 Distribution of points for measuring cylinder thickness

采用直尺（精度 1mm），測量CYT1、CYT2 和CYT3 柱殼周向0°、90°、180°、270°有效長度，統計分析如表4 所示，其中R為柱殼內半徑（R=d/2）。

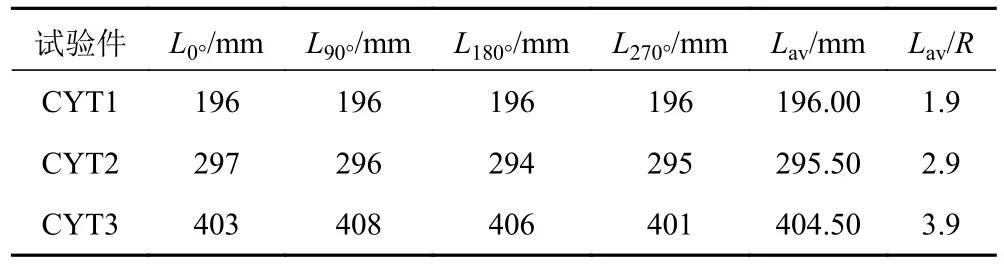
表4 柱殼有效長度Tab.4 Effective length of cylinders

選用OMNISCAN MX 相控陣探傷儀，對復合材料圓柱殼試驗件進行內部探傷檢測。以CYT1 為例，其周向0°、90°、180°、270°的軸向截面檢測分析結果如圖6 所示，上下淺色區域分別為圓柱殼外表面與內表面。由于纏繞工藝影響，外表面軸向方向的淺色區域呈微小波動起伏狀。90°截面掃面中部有深色帶狀區域，主要因制作工藝過程纖維錯位、殘留氣泡等因素引起，其他區域無明顯缺陷狀態，不影響靜水壓力試驗結果的普遍性。

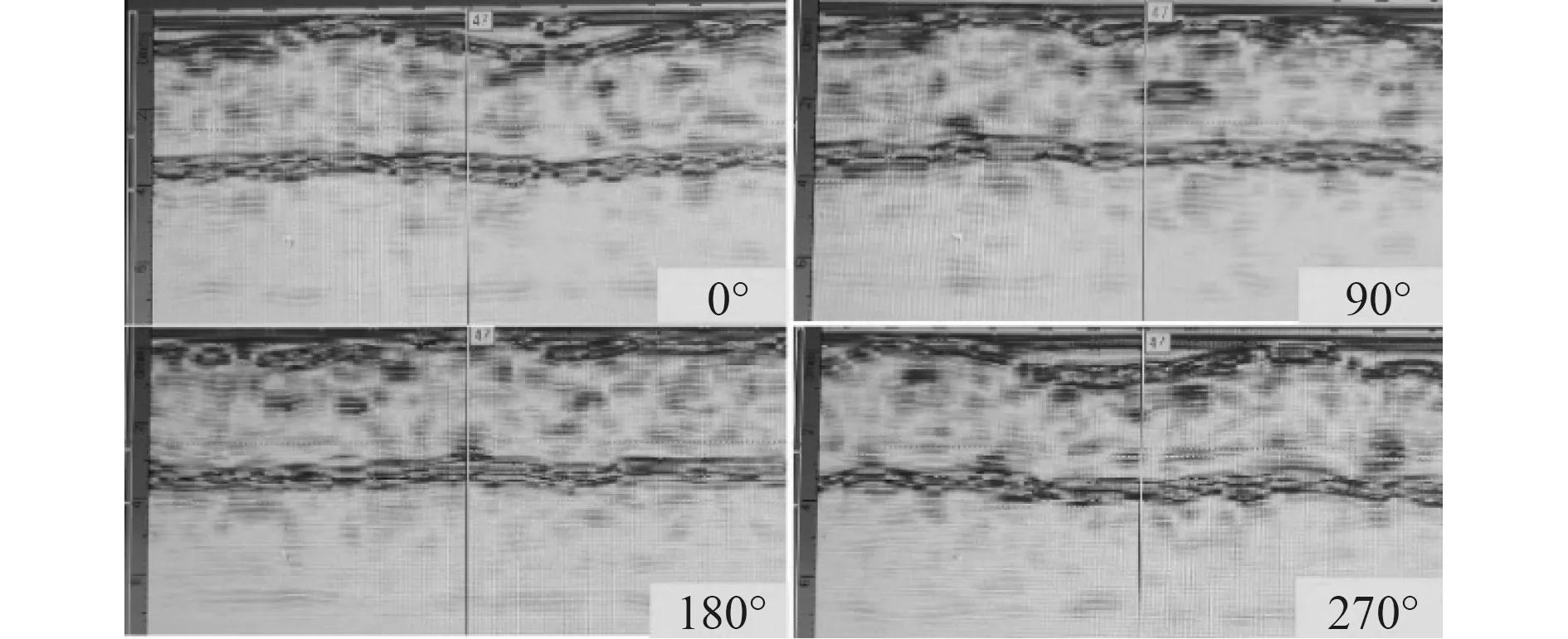
圖6 復合材料柱殼探傷檢測(CYT1)Fig.6 Flaw detection of composite cylinders (CYT1)

1.3 靜水壓力艙試驗

試驗壓力艙（內徑400 mm、高500 mm，量程0～8 MPa 且極限壓載10 MPa）采用靜水加壓，通過壓力傳感器（量程0～10 MPa，精度±0.1%）實時采集，采樣頻率50 Hz。因CYT3 浮力大于重力，在CYT3 下端蓋內表面粘接2 kg 配重，可使圓柱殼在加壓過程完全浸沒在水中。

依次將CYT1、CYT2 和CYT3 分別置于壓力艙內，采用手動閥逐步加壓，艙體內出現瞬間壓降，且伴隨巨大爆破聲，即可停止加壓，壓力艙內壓力變化如圖7 所示。因手動加壓方式，壓力曲線前端呈現鋸齒式增加趨勢。

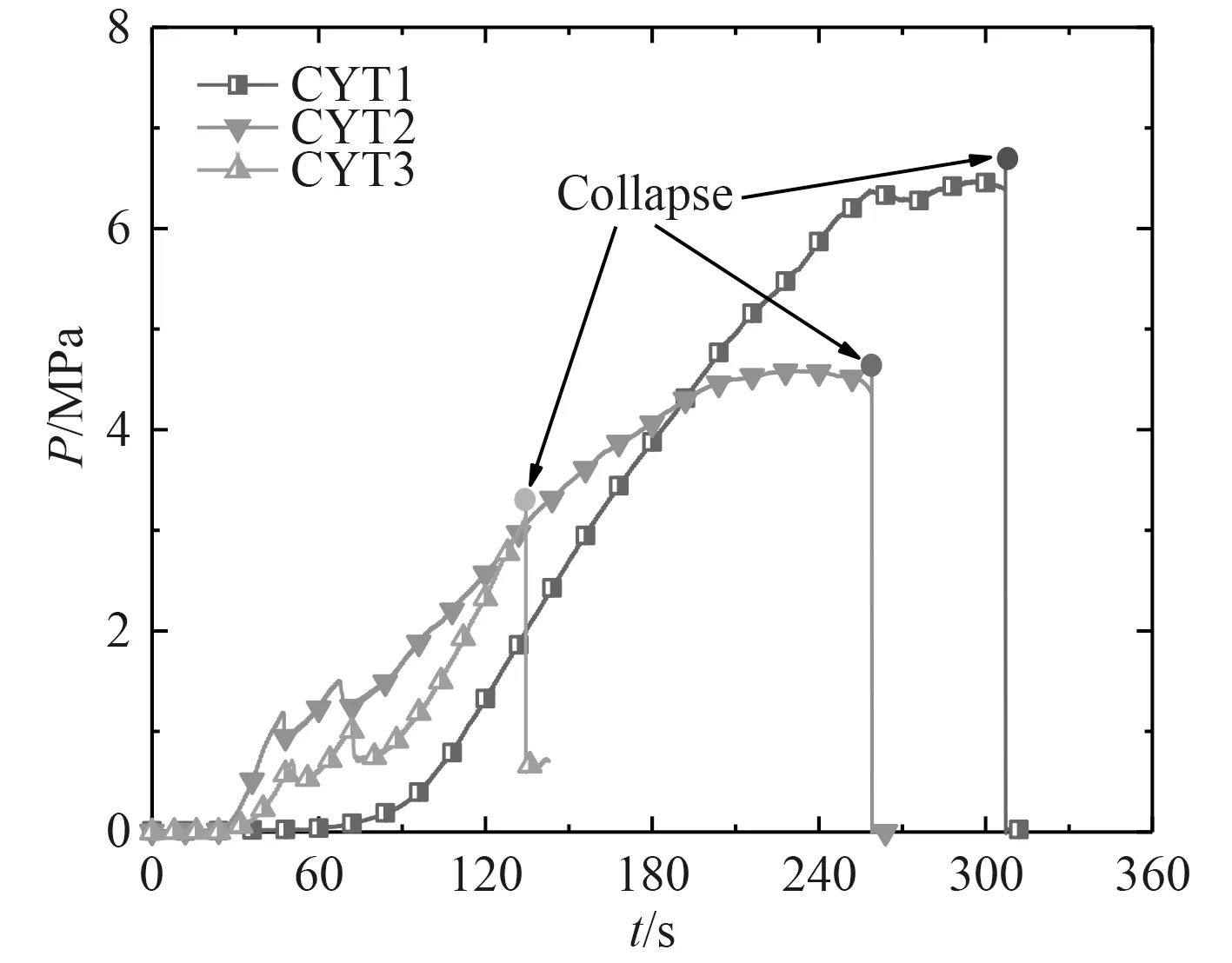
圖7 CYT 柱殼靜水加壓曲線Fig.7 Pressure–time curves obtained from the hydrostatic test of CYT cylinders

CYT3 曲線在加壓后程直線上升至壓潰，后壓降明顯。CYT1 與CYT2 承壓載荷分別在260～310 s、180～260 s 區間維持一段時間后，加載曲線徒增后瞬間直線下降。曲線峰值即為樣本破壞時的最大外壓載荷，CYT1、CYT2 和CYT3 柱殼最大破壞壓力分別為6.789 MPa、4.585 MPa 和3.251 MPa，壓潰形式如圖8 所示。

圖8 CYT 柱殼壓潰形式與裂痕路徑Fig.8 Typical final failure modes and crack propagation path of CYT cylinders

2 數學與數值模型

2.1 復合材料圓柱殼屈曲解析

1）NASA SP-8 700[7]

基于層合板理論，NASA SP-8 700 給出復合材料柱殼均勻受外壓下的屈曲載荷公式，如下式：

2）Shen 經驗公式[8]

Shen 提出適用于纖維纏繞的復合材料圓柱殼受均勻外壓下的屈曲載荷，如下式：

2.2 Hashin 失效及漸進損傷理論

復合材料層合板面內失效模式主要為纖維斷裂、纖維屈曲、基體開裂和基體擠裂。Hashin 強度準則針對4 種失效模式，分纖維方向拉伸、纖維方向壓縮、基體方向拉伸、基體方向壓縮等4 種失效判斷，兼顧不同失效模式對材料性能影響，應用較廣。Hashin[21]強度準則公式為：

其中：Fft為 纖維方向拉伸失效；Ffc為纖維方向壓縮失效；Fmt為基體方向拉伸失效；Fmc為基體方向壓縮失效。上述判定值達到1 時，損傷起始。

損傷起始后，材料剛度開始逐漸退化，進入損傷演化階段。采用基于能量損傷演化，剛度退化公式為：

2.3 數值模型

基于Abaqus 軟件建立復合材料圓柱殼有限元模型，圓柱殼為連續殼SC8R 單元，金屬封蓋為C3D8R單元，金屬封蓋與復合材料柱殼通過綁定約束連接。為消除模型剛性位移，選擇限制不共線3 個節點的6 個方向位移，該約束為虛約束，其支反力均約為0，能較好模擬柱殼靜水環境下受均布外壓工況[22]。邊界條件及網格收斂性驗證，如圖9 所示。為提高計算效率，且不影響計算精度，選擇單元尺寸為5 mm。

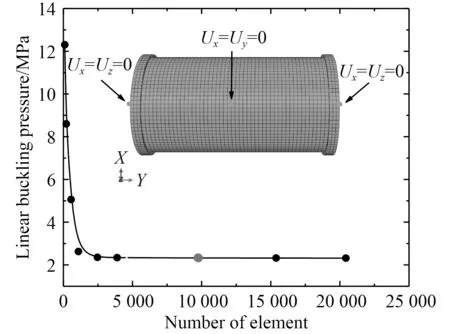
圖9 網格收斂性與邊界條件設置(CYT2)Fig.9 The convergence result of mesh size and boundary condition (CYT2)

復合材料柱殼外表面及兩端封蓋外均施加1 MPa均布壓力，建立試驗件模型及實驗樣本模型（圓柱殼長徑比：L/R；LRT1.0：L/R=1，LRT1.5：L/R=1.5，LRT5.0：L/R=5，LRT6.0：L/R=6，LRT7.0：L/R=7），進行線性屈曲分析。其中，基于CYT1、CYT2 和CYT3掃描模型線性屈曲分析結果如圖10 所示，其軸向波數均為1，周向波數分別為10、8、6。L/R增大，周向波數依次減少。此外，基于Hashin 強度準則及漸進損傷理論，采用弧長法， CYT1、CYT2 和CYT3 非線性屈曲結果如圖11 所示。CYT1、CYT2 和CYT3 圓柱殼后屈曲模態，中部均出現一處凹陷，與試驗破壞形式（柱殼中部塌陷，纖維及基體完全斷裂）一致。

圖10 CYT 復合材料柱殼線性屈曲模態Fig.10 Linear buckling modes of the CYT composite cylinders

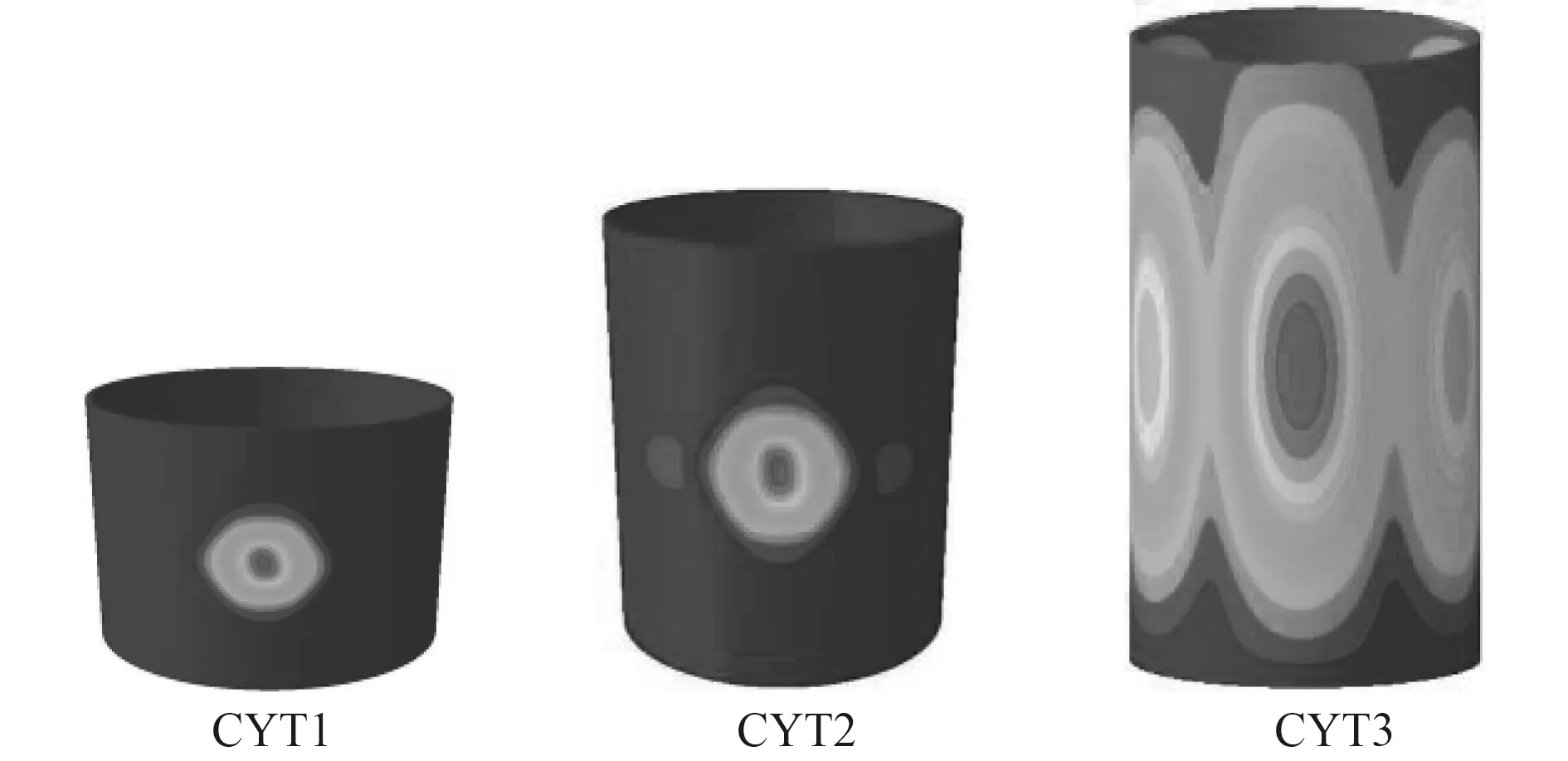
圖11 CYT 復合材料柱殼后屈曲模態Fig.11 Final nonlinear post-buckling modes of the CYT composite cylinders

3 結果分析

3.1 試驗結果分析

由圖10 可知，CYT1 與CYT2 圓柱殼中部一處塌陷，出現纖維完全斷裂破壞，且斷裂形式由外向內呈斜向斷裂。CYT1 圓柱殼纖維斷裂從中部分別反方向向兩端延伸，繼而在柱殼軸向1/3 處均分叉為2 條裂痕，裂痕一直延伸至封蓋，但封蓋與圓柱殼未分離，說明封蓋與圓柱殼粘接效果良好。分叉裂痕分別與圓柱殼軸向方向呈55°夾角，與纖維纏繞角度一致。Cho 等[23]設計纖維纏繞角為[±45°/90°]、[±60°/90°]圓柱殼，靜水壓潰后，其中部纖維完全斷裂，裂痕向兩端延展。在柱殼軸向約1/3 處裂痕分別呈45°、60°延伸，與本文試驗破壞結果類似。CYT2 圓柱殼中部纖維完全斷裂，以交叉反方向向兩端發展，分別至柱殼軸向1/3 處發展成2 條裂痕，且與軸向夾角均為55°。CYT2 上端右側裂痕與下端左側裂痕均延長至封蓋處。CYT3 圓柱殼外表面軸向兩端1/3 處分別出現兩處長4.6 mm、4.8 mm 裂痕，其他區域未破壞，如圖12 所示。Hur 等[24]設計的圓柱殼（長569 mm，壁厚2.612 mm）其破壞形式為兩處平衡于軸向的細小斷裂痕，與試驗結果類似。

圖12 CYT3 復合材料柱殼纖維斷裂Fig.12 Fiber breakage of the CYT3 composite cylinder

為表征圓柱殼內表面破壞形式，選擇在圓柱殼一端封蓋與柱殼交接處進行切割。CYT1、CYT2 和CYT3 圓柱殼內表面壓潰形式，如圖13 所示。CYT1、CYT2 和CYT3 圓柱殼破壞均在一側，且斷裂破壞均以中部向兩端擴散。CYT1、CYT2 和CYT3 圓柱殼破壞范圍占比依次減小，破壞程度也依次降低。

圖13 CYT 圓柱殼內部失效區域Fig.13 Typical final failure area of CYT cylinders

3.2 數學與數值模型結果分析

根據式（1）、式（2）及Abaqus 分析軟件獲得試驗件CYT1、CYT2 和CYT3 屈曲載荷，如表5 所示，其與試驗載荷值比值分別為0.8 4 5 0 ～0.9 7 9、0.728～0.822、0.913～1.007、0.891～0.992。式（2）計算結果相對較為保守；與CYT1、CYT2 和CYT3 試驗載荷值誤差分別為17.8%、21.2%、24.1%。NASA 公式計算結果更為接近實驗值，與C Y T 1、C Y T 2 和CYT3 試驗載荷值誤差分別為2.1%、14.1%、15.5%。長徑比L/R越大，理論與試驗值誤差越大。

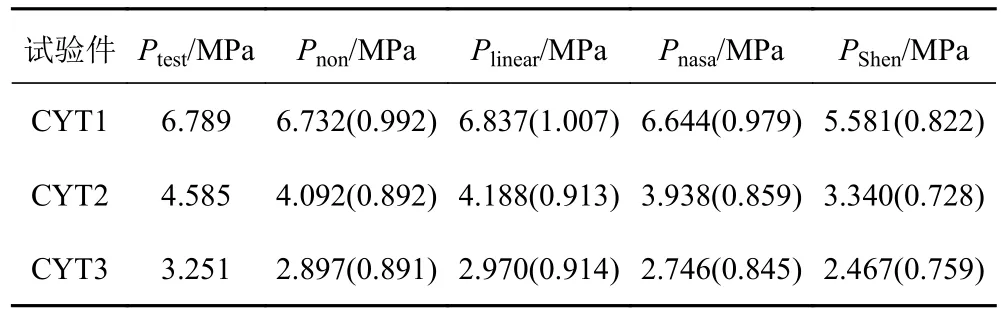
表5 試驗件數值（Pnon）、理論載荷值（Pnasa /PShen）對比及其與靜水壓力載荷比值Tab.5 Numerical (Pnon), and theoretical (Pnasa /PShen) buckling loads of composite cylinders; the ratio of the calculated values to test values is indicated in parentheses

CYT2 和CYT3 圓柱殼線性屈曲載荷與試驗值誤差分別為8.7%、8.6%，弧長法誤差分別為10.8%、10.9%。因此，對于長徑比L/R＞2.9 采用線性屈曲分析預測結果相比考慮材料漸進損傷的弧長法較為接近。CYT1（L/R＜2.9）采用線性屈曲載荷高于實驗值，宜采用考慮材料漸進損傷的弧長法更為保守，其誤差為0.8%。上述模型結果（除CYT1-Plinear載荷值外）與試驗載荷比值均小于1，可見采用層合板模型預測單一螺旋纏繞復合材料圓柱殼屈曲載荷相對保守。表6 為針對實驗樣本模型（LRT1.0：L/R=1；LRT1.5：L/R=1.5；LRT5.0：L/R=5；LRT6.0：L/R=6；LRT7.0：L/R=7），分別采用Abaqus、NASA 和Shen 方法獲得的載荷值。

表6 數值、NASA 和Shen 方法求解不同L/R 柱殼的載荷值Tab.6 Comparison of buckling loads calculated using Abaqus,NASA, and Shen

圖14 為屈曲載荷隨L/R值變化曲線，復合材料圓柱殼隨長徑比增大，其承載壓力緩慢下降，本文試驗結果與金屬圓柱殼類似[25]。可知，L/R＜2.8時，圓柱殼長徑比減小，Abaqus 線性屈曲、NASA 和Shen 方法計算的屈曲載荷值陡增，且LRT1.0 與LRT7.0 載荷比值分別為7.972、11.481、10.517。相比上述方法，Abaqus 弧長法屈曲載荷增加緩慢，且LRT1.0 與LRT7.0 載荷比值為7.501。

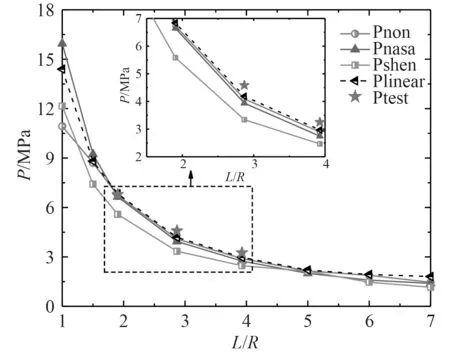
圖14 CYT 圓柱殼理論與試驗屈曲載荷對比Fig.14 Theoretical and experimental buckling results of CYT cylinders

4 結 語

本文基于復合材料層合板理論，建立了螺旋纏繞復合材料圓柱殼層合板等效有限元模型。分析比較理論模型、有限元模型和靜水壓力試驗結果，討論了不同長徑比對復合材料圓柱殼屈曲特性的影響規律。通過研究得到以下結論：

1）復合材料圓柱殼試驗破壞，其殼體穩定性占主要因素。圓柱殼L/R＜2.9，其在發生失穩后，雖未完全喪失承載能力，但承載載荷已達極限，材料剛度開始退化，最終達到強度極限，出現強度破壞；L/R＞2.9，圓柱殼破壞直接由失穩引起。

2）NASA 規范與Shen 理論值及試驗載荷比值均小于1（0.728～0.979），采用層合板理論模型預測單一螺旋纏繞復合材料圓柱殼屈曲載荷相對保守。理論模型預測結果最小誤差2.1%，最大誤差15.5%，且長徑比L/R越大，理論與試驗值誤差越大。

3）對于L/R＞2.9，采用線性屈曲分析預測結果相比考慮材料漸進損傷的弧長法較為接近試驗載荷值，最大誤差為8.7%；L/R＜2.9，宜采用材料漸進損傷模型預測更為保守，其誤差為0.8%。