高能量電子激發(fā)比壓阿爾芬本征模的全域模擬研究*

包健 張文祿 李定

(中國科學院物理研究所,軟物質(zhì)物理實驗室,北京 100190)

采用自主開發(fā)的本征值程序MAS,基于朗道流體-漂移動理學混合物理模型,針對近期實驗上觀測到的高能量電子激發(fā)比壓阿爾芬本征模(e-BAE)開展動理學模擬研究.通過在全域環(huán)幾何位形下非微擾求解e-BAE色散關系,得到了e-BAE 實頻率、增長率和模結構隨環(huán)向模數(shù)的變化特征,并發(fā)現(xiàn)e-BAE 在高能量電子密度-溫度參數(shù)空間下存在不穩(wěn)定島,而在傳統(tǒng)微擾理論下則不存在不穩(wěn)定島.進一步分析了高能量電子非微擾效應對e-BAE 模結構對稱性破缺的影響,結果表明: 增大高能量電子溫度可以引起顯著的極向?qū)ΨQ性破缺;移動高能量電子密度剖面使其驅(qū)動強度關于有理面不對稱時,e-BAE 模結構產(chǎn)生徑向?qū)ΨQ性破缺,并且擾動幅度在平行波數(shù)譜空間下分布不對稱,從而引起等離子體自發(fā)旋轉(zhuǎn).本文研究結果為理解實驗上e-BAE 的激發(fā)與傳播特征具有參考意義.

1 引言

隨著托卡馬克上中性束和射頻波加熱功率的提升,大量高能量粒子(energetic particles,EP)會在輔助加熱過程中產(chǎn)生[1],不同能量和投擲角的EP 可以通過波-粒子共振激發(fā)各類阿爾芬本征模[2,3],進一步造成EP 輸運和等離子體約束水平下降[4].近期,我國HL-2A 裝置上電子回旋波加熱實驗首次證實了高能量電子可以激發(fā)比壓阿爾芬本征模(energetic electron driven beta-induced Alfvén eigenmode,e-BAE)[5],EAST 裝置在相似實驗條件下也觀測到類似e-BAE 的磁流體不穩(wěn)定性[6],由于高能量電子的歸一化軌道及特征頻率與未來聚變堆等離子體中的α 粒子相接近,理解高能量電子激發(fā)低頻磁流體不穩(wěn)定性對研究α 粒子物理具有重要借鑒意義[7].

針對e-BAE 的激發(fā)機制和飽和機制已開展了一系列理論和初始值模擬研究,發(fā)現(xiàn)深度捕獲高能量電子通過進動共振激發(fā)e-BAE[8-11],并且共振高能量電子的非線性響應對e-BAE 產(chǎn)生帶狀流具有重要貢獻[12].然而,由于不同研究手段的局限性,e-BAE 的線性性質(zhì)尚未被完全理解.例如理論上采用氣球模表象求解e-BAE 色散關系,其要求平衡剖面和模結構具有較大的尺度分離[13],無法準確描述低環(huán)向模數(shù)的情況;而初始值模擬采用粒子-網(wǎng)格方法,包含高能量電子的動理學效應,一方面時空步長受到真實電子質(zhì)量的嚴格約束[14],另一方面需要模擬大量粒子降低數(shù)值噪聲,由于計算量大難以在參數(shù)空間中進行大量掃描.

本征值模擬是研究e-BAE 線性物理性質(zhì)的有效方法,一方面將物理方程在托卡馬克全域環(huán)幾何位形下離散并轉(zhuǎn)換為矩陣本征值問題進行求解,不依賴于空間尺度分離假設;另一方面對時間進行傅里葉變換,無需在時域上演化物理量,極大節(jié)省了計算量.基于朗道流體物理模型的MAS 本征值程序可以包含主等離子體的動理學效應,已被用于分析常見的阿爾芬本征模,包括環(huán)形阿爾芬本征模、反磁剪切阿爾芬本征模和比壓阿爾芬本征模等[15-17].近期MAS 程序中加入了高能量電子物理,通過求解漂移動理學方程得到擾動分布函數(shù),包含重要的動理學非絕熱響應和流體對流響應,并且經(jīng)過與第一性原理粒子-網(wǎng)格程序GTC 校驗,MAS 程序可以準確計算e-BAE 的模結構和色散關系.圍繞目前實驗上重點關注的高能量電子激發(fā)e-BAE 溫度/密度閾值及模結構對稱性破缺兩個重要問題,本文采用MAS 程序在參數(shù)空間下開展e-BAE 的動理學模擬研究.

本文第2 節(jié)介紹模擬采用的朗道流體-漂移動理學混合物理模型;第3 節(jié)分析了e-BAE 實頻率和增長率對環(huán)向模數(shù)、高能量電子溫度和密度的依賴關系,以及高能量電子非微擾效應引起的e-BAE模結構對稱性破缺;第4 節(jié)是總結和討論.

2 物理模型

MAS 程序采用朗道流體模型描述主等離子體,漂移動理學模型描述高能量電子,二者構成一個非微擾的混合物理模型,自洽包含主等離子體抗磁漂移、朗道阻尼、有限拉莫爾半徑,以及捕獲高能量電子進動共振等重要動理學效應.MAS 程序求解的方程組包括渦量方程、平行方向歐姆定律、離子壓強方程、平行方向動量方程和離子連續(xù)性方程,具體形式依次為[15,16]

電子擾動密度 δne和電子平行方向擾動速度 δu//e分別通過準電中性條件和平行方向安培定律進行求解:

高能量電子擾動密度 δnh、平行方向擾動速度 δu//h和擾動壓強 δPh由其擾動分布函數(shù)在速度空間積分得出,并且通過(1)式、(9)式和(10)式與主等離子體朗道流體模型進行耦合,具體形式是

3 模擬結果

3.1 平衡參數(shù)

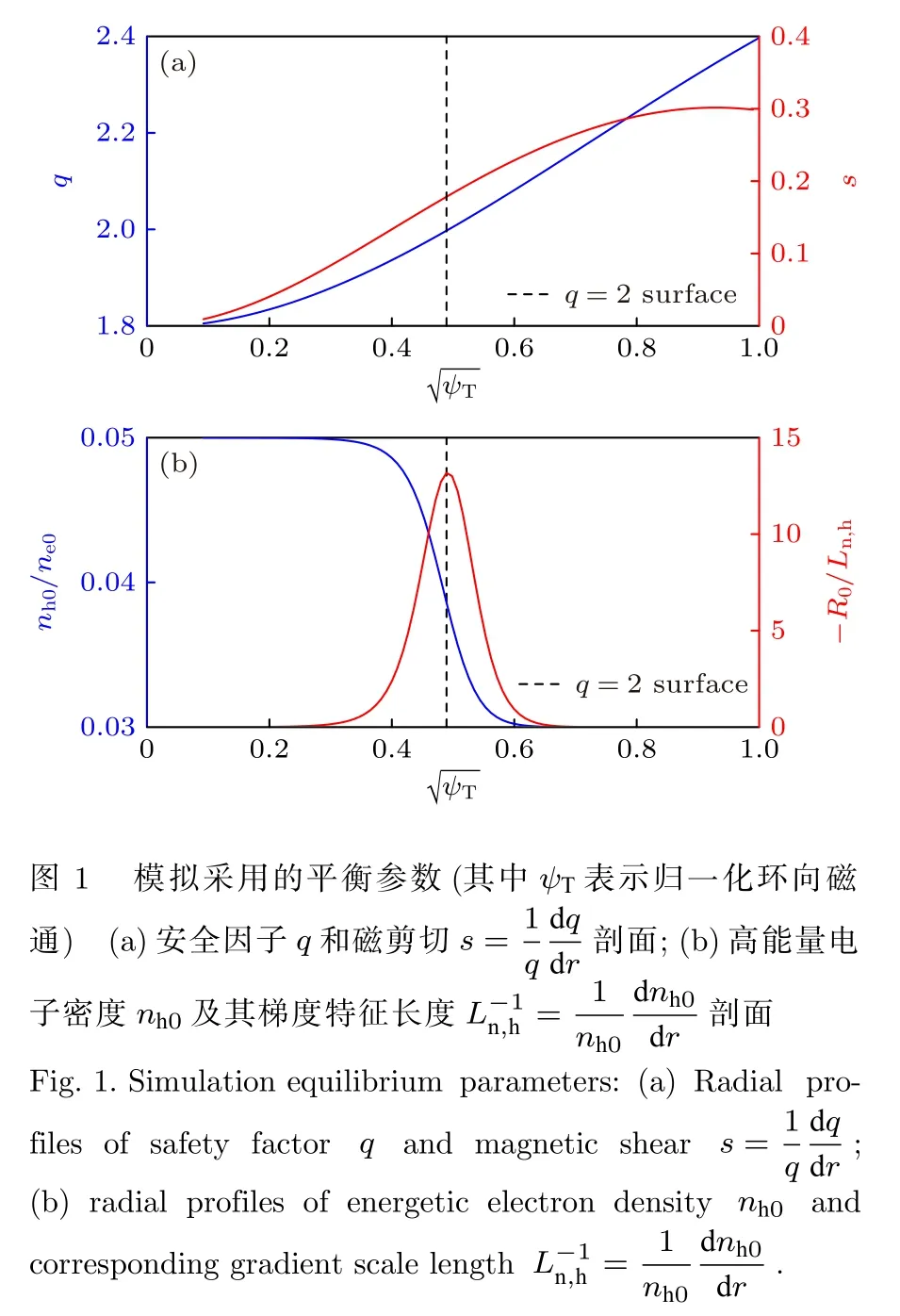
為了分析e-BAE 的主要物理特點,本文采用文獻 [10]中的同心圓截面解析平衡參數(shù)進行計算,具體包括: 磁軸處磁場強度大小B0=1.91 T、大半徑R0=0.65 m、小半徑a=0.333R0,安全因子q和磁剪切s=(1/q)(dq/dr) 剖面如圖1(a)所示.采用質(zhì)子為主離子(電荷為Zi=e),主離子和主電子、高能量電子溫度均勻分布,分別為Ti0=Te0=500 eV和Th0=25Te0.主電子密度均勻分布ne0=1.3×1014cm-3,高能量電子密度nh0剖面如圖1(b)所示.在q=2 有理面處驅(qū)動強度最大|R0/Ln,h|max=12.7,其中Ln,h=(?nh0/nh0)-1為梯度特征長度,主離子密度ni0則由準電中性條件Zini0+qe(ne0+nh0)=0確定.

3.2 阿爾芬連續(xù)譜與e-BAE 特征

首先在不同環(huán)向模數(shù)n下,計算理想磁流體連續(xù)譜和e-BAE 本征模,如圖2 所示.在q=2 有理面附近,m=nq的極向分量形成連續(xù)譜勢阱,其最低極值點是BAE 連續(xù)譜積累點(continuum accumulation point,CAP)[18],并且BAE-CAP 的頻率不隨n變化.結合圖2 和圖3 可以發(fā)現(xiàn),在n=2增大到n=5 的過程中,連續(xù)譜勢阱逐漸變窄,由于BAE 本征模是動理學阿爾芬波束縛在連續(xù)譜勢阱內(nèi)形成的[19],因此e-BAE 模結構的徑向?qū)挾纫蚕鄳冋?在圖3(a1)—(d1)中,e-BAE 靜電勢δφ的二維模結構呈現(xiàn)“回旋鏢”形狀,這是由高能量電子非微擾效應造成的: 即(15)式代入(1)式后,渦量方程(1)包含反厄米分量貢獻,引起e-BAE 極向模結構具有上-下不對稱性,這與近期e-BAE 的氣球模理論研究結論相似[9],并且在高能量離子激發(fā)BAE 的理論和模擬研究中也觀察到對稱性破缺現(xiàn)象[20,21];另一方面,如圖3(a2)—(d2)所示,e-BAE 由一個主極向分量和兩個邊帶極向分量組成,主極向分量在q=2 有理面處滿足共振條件m=nq且幅度遠大于邊帶極向分量,因此e-BAE 呈現(xiàn)弱氣球模結構.

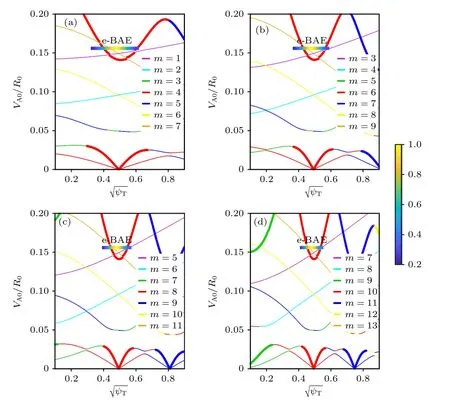
圖2 (a)—(d)環(huán)向模 數(shù) n=2,n=3,n=4和n=5 的連續(xù)譜,其中細線代表聲波,粗線代表阿爾芬波,彩色代表歸一化的e-BAE 振幅強弱;縱軸刻度單位是 VA0/R0 (即 磁軸處阿爾芬頻率),其中 VA0=B0,a/ 為磁軸處阿爾芬速度,R0 為 磁軸處大半徑,B0,a 為磁軸處磁場,ni0,a 為磁軸處離子密度Fig.2.(a)-(d) Continuous spectra of toroidal mode numbers n=2,n=3,n=4 and n=5,where the thin line represents the acoustic branch,the thick line represents the Alfvénic branch,and the colorbar represents the normalized radial amplitude of e-BAE.

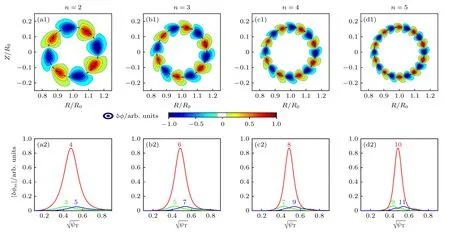
圖3 (a1)—(d1)環(huán)向模數(shù) n=2,n=3,n=4和n=5 的e-BAE 靜電勢 δφ 二維模結構;(a2)—(d2)各極向傅里葉分量剖面Fig.3.(a1)-(d1)The 2D poloidal mode structures of electrostatic potential δφ of toroidal mode numbers n=2,n=3,n=4 and n=5;(a2)-(d2) radial profiles of each poloidal harmonics.

進一步分析e-BAE 色散關系: 實頻率主要是由BAE-CAP 決定的,幾乎不隨n變化,如圖4 藍線所示.盡管高能量電子抗磁漂移頻率ω?n,h和ω*T,h與n成正比,自由能在高n時更容易釋放,但由于捕獲高能量電子通過進動共振驅(qū)動e-BAE,因此共振條件匹配度ζ=ω/ωD0與n成反比,最終使得e-BAE 增長率隨n先增大后降低,如圖4 紅線所示.

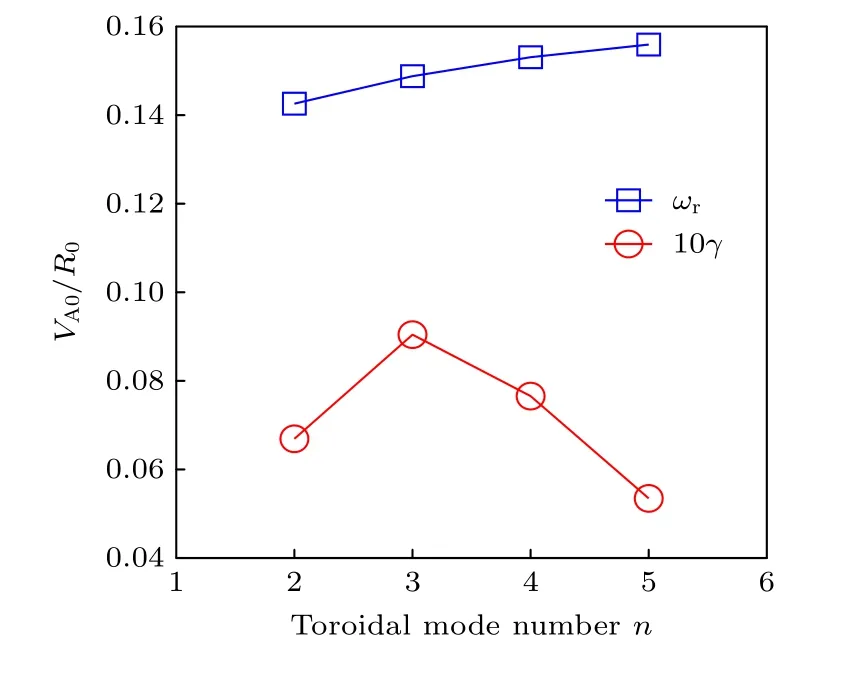
圖4 e-BAE 實頻率和增長率隨環(huán)向模數(shù) n 的變化,其中縱軸刻度單位是 VA0/R0 (即磁軸處阿爾芬頻率)Fig.4.The e-BAE real frequency and growth rate dependences on the toroidal mode number n.

3.3 高能量電子溫度和密度對e-BAE 色散關系的影響

傳統(tǒng)研究通常采用微擾方法計算高能量粒子激發(fā)阿爾芬本征模,即求解主等離子體方程計算阿爾芬本征模實頻率和模結構,再代入到EP 貢獻項中計算增長率[22].隨著實驗上加熱功率的提高,EP 與主等離子體的比壓已經(jīng)接近,實驗和第一性原理模擬研究均表明EP 對阿爾芬本征模實頻率和模結構的非微擾效應不可忽略[23-25].為了更加符合當前EP 實驗情況,MAS 程序采用非微擾模擬方法,自洽包含高能量電子貢獻項對模結構、實頻率和增長率的影響.這里選取圖4 中最不穩(wěn)定的n=3 e-BAE,計算實頻率和增長率在nh0,a-Th0參數(shù)空間中的分布,這里nh0,a代表磁軸處的高能量電子密度值,另外本文模擬中高能量電子溫度分布均勻,因此采用Th0代表其溫度值.如圖5(a)所示,實頻率ωr隨著nh0,a和Th0增大而降低,這是由于方程(14)代入(1)式后磁流體交換模項增大造成的[18];另一方面,由于ωr隨nh0,a的變化影響了共振條件匹配度ζ=ω/ωD0,因此增長率γ不再隨nh0,a單調(diào)增大,而是隨nh0,a先增大后降低,形成圖5(b)中的不穩(wěn)定島;另外MAS 模擬同時包含高能量電子驅(qū)動效應和背景等離子體阻尼效應,只有對于圖5(b)中青藍色實線(γ=0)邊界內(nèi)的nh0,a和Th0參數(shù)區(qū) 間,e-BAE 才可以不穩(wěn)定,激發(fā)e-BAE 的最低高能量電子比壓 min(βh,crit) 對應的nh0,a和Th0如圖5(b)中紅色五角星所示.

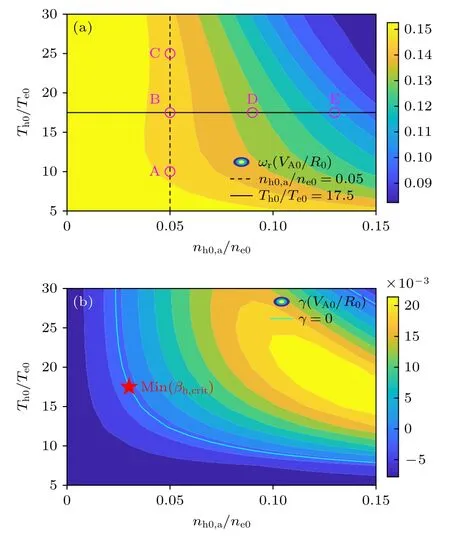
圖5 e-BAE (a)實頻率和(b)增長率隨高能量電子密度和溫度的依賴關系.A—E 為參數(shù)空間下的5 個代表算例,用于下一步模結構分析.青藍色實線為e-BAE 臨界不穩(wěn)定邊界 (γ=0),五角星為激發(fā)e-BAE 需要的最小高能量電子比壓對應的密度和溫度值Fig.5.The e-BAE (a) real frequency and (b) growth rate dependences on energetic electron (EE) density and temperature.A—E are five typical cases for next mode structure analysis.Cyan solid line represents the boundary of marginal stable e-BAEs with γ=0,and the pentagram marks the EE density and temperature locations of the minimal value of EE βh required for e-BAE excitation.

3.4 e-BAE 模結構對稱性破缺

如前文所述,e-BAE 模結構具有“回旋鏢”形狀特征,屬于典型的極向?qū)ΨQ性破缺,為了進一步明確nh0,a和Th0對e-BAE 模結構的影響,將圖5(a)中A—E 五個算例分為兩組進行內(nèi)部比較: 算例A,B,C 中高能量電子密度相同nh0,a=0.05ne0,溫度分別為Th0/Te0=10,Th0/Te0=17.5和Th0/Te0=25 ;算例B,D,E 中高能量電子溫度相同Th0/Te0=17.5,密度分別為nh0,a=0.05ne0,nh0,a=0.09ne0和nh0,a=0.13ne0.如圖6 所示: 算例A,B,C 中模結構的“回旋鏢”形狀特征依次增強,并且對于m=6的主極向分量,其相位角沿著徑向的變化增大(藍色實線),說明有限Th0對應的非微擾效應既導致ωr降低,也加劇了模結構的極向?qū)ΨQ性破缺.如圖7 所示,算例B,D,E 中模結構的“回旋鏢”形狀相似,m=6 主極向分量的相位角θr變化也基本一致,說明有限nh0對應的非微擾效應主要引起ωr降低,而對e-BAE 模結構的影響很小.

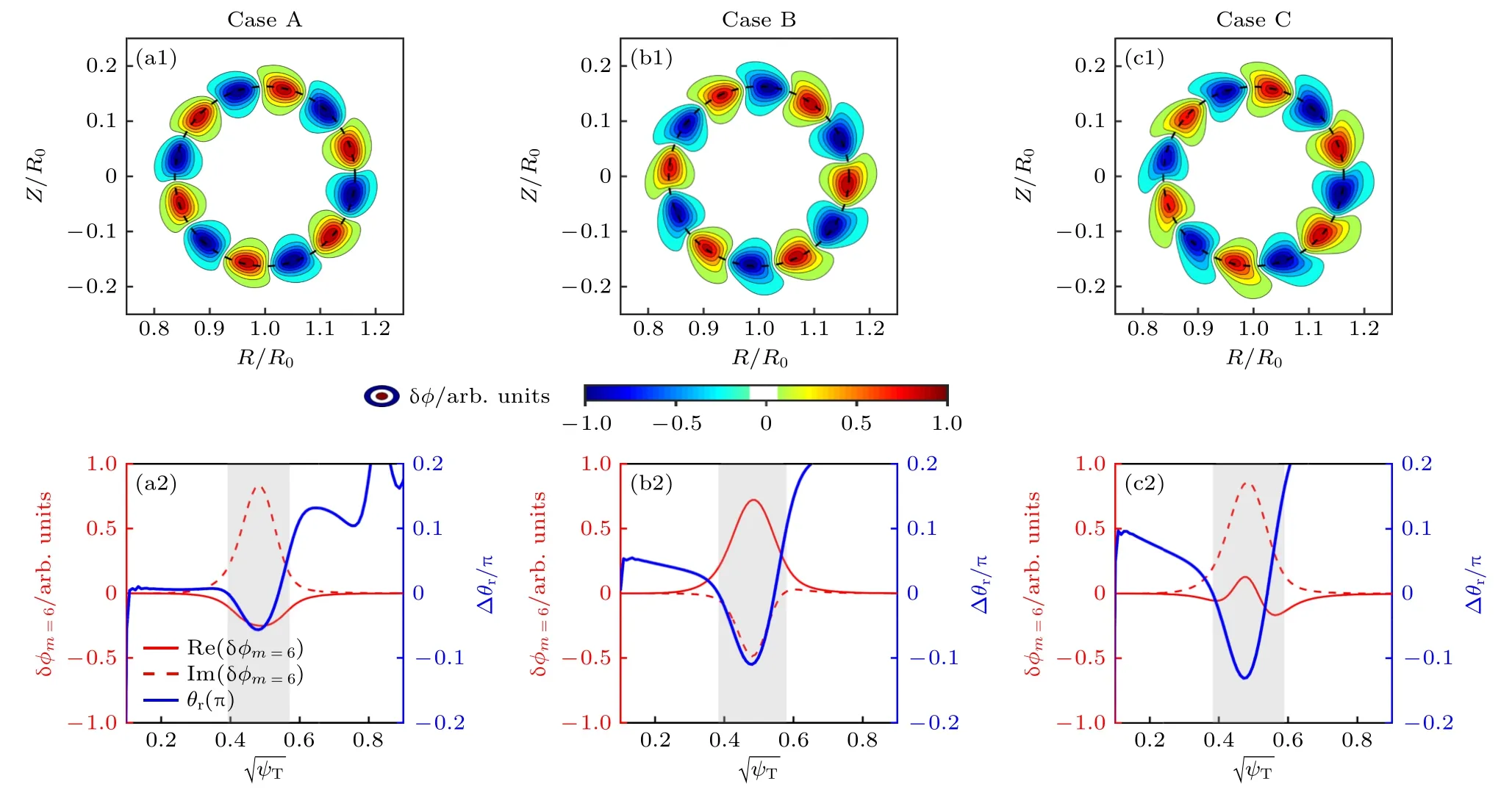
圖6 (a1)—(c1)圖5 中A,B,C 算例的靜電勢 δφ 二維模結構;(a2)—(c2) A,B,C 算例中主極向分量 δφm=6 及其相位角θr=arctan的徑向剖面,灰色陰影部分表示e-BAE 有限振幅區(qū)域Fig.6.(a1)-(c1) The 2D poloidal mode structures of electrostatic potential δφ for cases A,B and C in Fig.5;(a2)-(c2) the radial profiles of dominant principal poloidal harmonic of δφm=6 and corresponding phase angle θr=arctan,and the gray shaded region represents the radial domain with finite e-BAE amplitude.

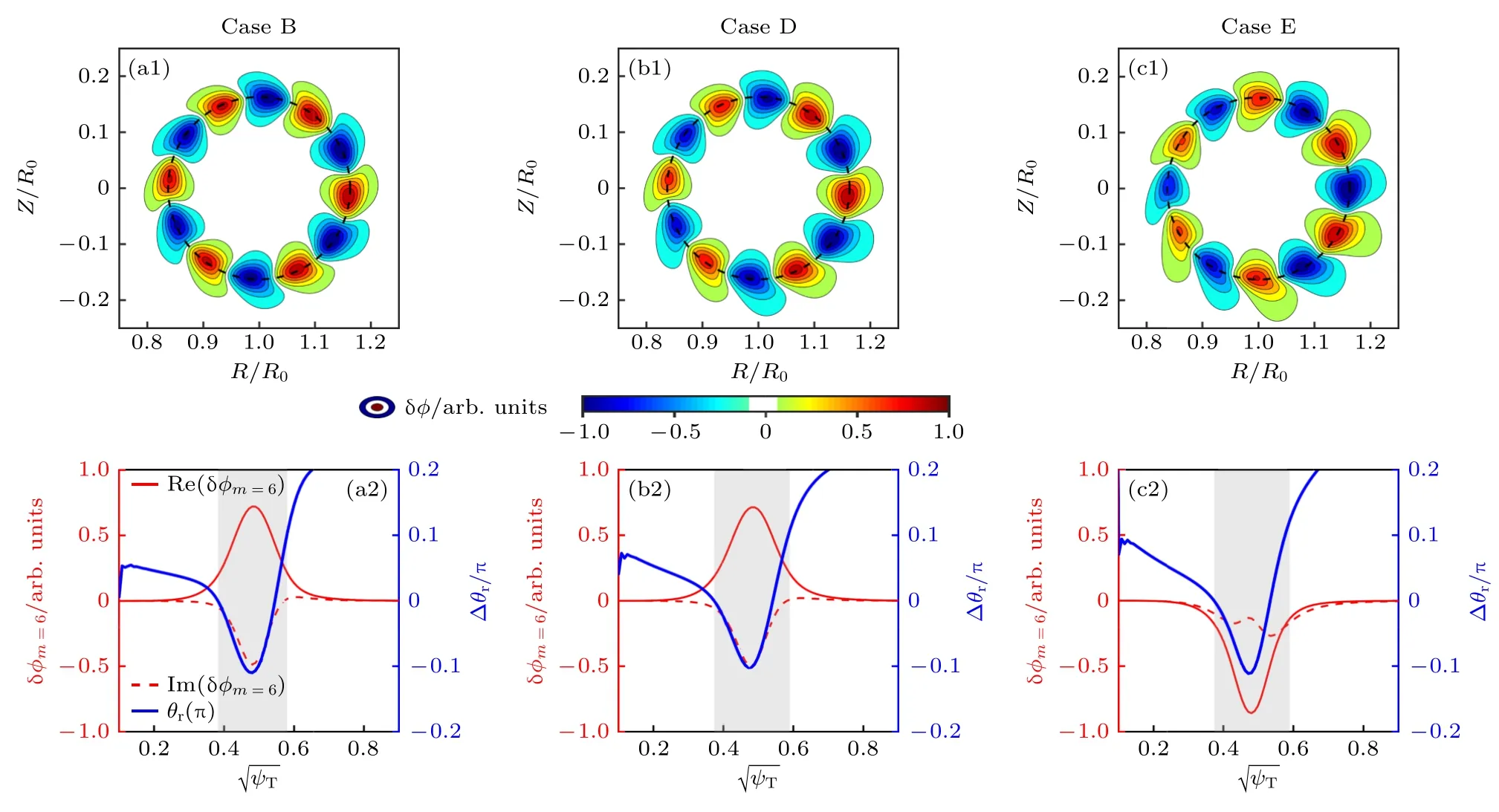
圖7 (a1)—(c1)圖5 中B,D,E 算例的靜電勢δφ 二維模結構;(a2)—(c2) B,D,E 算例中主極向分量 δφm=6 及其相位角θr=arctan的徑向剖面,灰色陰影部分表示e-BAE 有限振幅區(qū)域Fig.7.(a1)-(c1) The 2D poloidal mode structures of electrostatic potential δφ for cases B,D and E in Fig.5;(a2)-(c2) the radial profiles of dominant principal poloidal harmonic of δφm=6 and corresponding phase angle θr=,and the gray shaded region represents the radial domain with finite e-BAE amplitude.

高能量電子非微擾效應不僅使e-BAE 模結構產(chǎn)生極向?qū)ΨQ性破缺,當其密度或溫度梯度的特征長度剖面(即 |R0/Ln,h| 或 |R0/LT,h|)關于有理面不對稱時,還會引起模結構的徑向?qū)ΨQ性破缺.通過變化最強驅(qū)動 |R0/Ln,h|max與q=2 有理 面的 相對位置,選取了3 個算例分析徑向?qū)ΨQ性破缺,如圖8(a)所示,采用圖5 中算例C的nh0,a=0.05ne0和Th0/Te0=25 參數(shù)作為“零偏移(zero shift)”算例,向左和向右移動nh0剖面作為“左偏移(left shift)”和“右偏移(right shift)”算例.如圖8(b)所示: “左偏移”、“零偏移”和“右偏移”算例中|R0/Ln,h|max對應的徑向位置分別為rmax(-R0/Ln,h)/a=0.41,rmax(-R0/Ln,h)/a=0.49和rmax(-R0/Ln,h)/a=0.57,并且只有“零偏移”算例的 |R0/Ln,h|max位置與q=2 有理面重合.圖9(a1)—(c1)分別為“左偏移”、“零偏移”和“右偏移”算例的 δφ二維模結構: 當最強驅(qū)動|R0/Ln,h|max的徑向位置向左和向右偏離q=2 有理面時,δφ模結構強度分布也向左和向右偏移,“回旋鏢”模結構產(chǎn)生顯著的徑向不對稱性.圖9(a2)—(c2)為m=6 主極向分量及其相位角θr,發(fā)現(xiàn)只有“零偏移”算例中相位角變化 Δθr的極值點在灰色陰影區(qū)域的中間(即關于q=2 有理面對稱),而“左偏移”和“右偏移”算例中 Δθr極值點分別在灰色陰影區(qū)域的右側和左側,與 δφ模結構強度分布偏移正好相反.

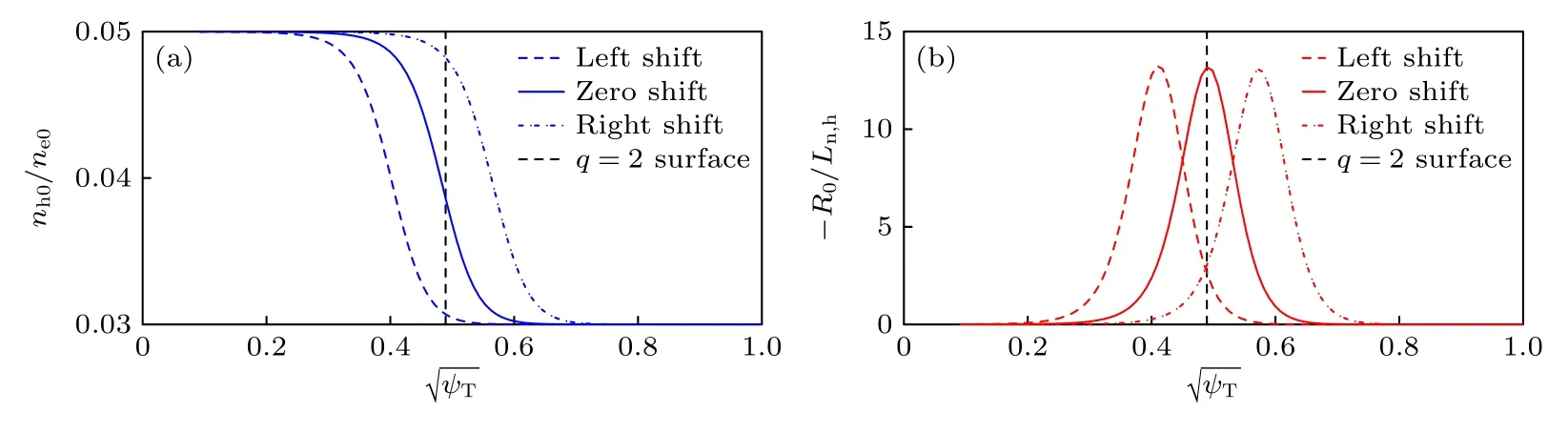
圖8 (a)固定高能量電子在磁軸處的密度 nh0,a/ne0=0.05,向左和向右移動高能量電子密度剖面;(b)對應的密度梯度特征長度剖面Fig.8.(a) Fix the on-axis EE density with nh0,a/ne0=0.05 and shift the density profile left and right;(b) the corresponding gradient scale length profiles.

徑向?qū)ΨQ性破缺還會導致 δφ擾動在平行波數(shù)k//=(nq-m)/(qR0)譜空間中分布不對稱,從而產(chǎn)生有限 〈k//|δφ|2〉V及相應的殘余協(xié)強(〈·〉V代表體積平均值),是驅(qū)動等離子體自發(fā)旋轉(zhuǎn)的重要機制之一[26].基于圖9 中3 個算例的模結構,計算相應的k//|δφ|2徑向剖面和體積平均值 〈k//|δφ|2〉V,如圖10(a)和圖10(b)所示,發(fā)現(xiàn)“左偏移”和“右偏 移”算例的k//|δφ|2剖面 關于q=2 有理面不 對稱,并且 〈k//|δφ|2〉V具有有限值;“零偏移”算例具有對稱的k//|δφ|2,由于正負區(qū)域相互抵消導致〈k//|δφ|2〉V接近于零.以上計算表明當高能量電子驅(qū)動強度關于有理面分布不對稱時,e-BAE可以引起有理面附近局域的等離子體自發(fā)旋轉(zhuǎn).

4 總結和討論

為了深入理解e-BAE 不穩(wěn)定性特征,本文利用自主開發(fā)的MAS 本征值程序開展全域動理學模擬研究.模擬采用朗道流體模型描述主等離子體,漂移動理學模型描述高能量電子,非微擾地在參數(shù)空間下計算e-BAE 模結構、實頻率和增長率.主要結果和發(fā)現(xiàn)如下:

1)隨著環(huán)向模數(shù)n增大,e-BAE 所在的阿爾芬連續(xù)譜勢阱寬度變窄,從而導致e-BAE 徑向模結構寬度變窄;但BAE-CAP 頻率不隨n變化,因此e-BAE 頻率隨n變化很小;e-BAE 增長率受到進動共振匹配條件的影響,隨n先增大后降低.

2)本文的亮點是通過計算不同nh0,a和Th0下e-BAE 實頻率和增長率,發(fā)現(xiàn)高能量電子非微擾效應可以定性改變e-BAE 色散關系圖譜: 即e-BAE實頻率隨nh0,a增大而顯著降低,進而影響共振條件導致增長率隨nh0,a先增大后降低.而傳統(tǒng)微擾方法則認為阿爾芬本征模實頻率不受nh0,a的影響,增長率隨nh0,a單調(diào)增大.另一方面,e-BAE 實頻率和增長率隨Th0的變化與nh0趨勢相似,導致e-BAE增長率在nh0,a-Th0參數(shù)空間存在不穩(wěn)定島,而微擾方法下則不存在不穩(wěn)定島.

3)高能量電子非微擾效應引起e-BAE 模結構對稱性破缺.當驅(qū)動強度剖面 |R0/Ln,h| 關于有理面對稱時,δφ二維模結構僅產(chǎn)生極向?qū)ΨQ性破缺,呈現(xiàn)沿極向上-下不對稱但關于有理面對稱的“回旋鏢”特征;當 |R0/Ln,h| 剖面關于有理面不對稱時,δφ二維模結構同時存在極向和徑向?qū)ΨQ性破缺,即“回旋鏢”模結構不再關于有理面對稱,通過計算發(fā)現(xiàn)徑向?qū)ΨQ性破缺可以產(chǎn)生有限 〈k//|δφ|2〉V并引起等離子體自發(fā)旋轉(zhuǎn).

本文重點分析了高能量電子非微擾效應對e-BAE 線性性質(zhì)的影響.下一步計劃研究主等離子體溫度、密度以及高能量電子各向異性分布函數(shù)的影響,并結合機器學習在參數(shù)空間下訓練高效代理模型[27],為理解和預測實驗上e-BAE 不穩(wěn)定性提供支持.

感謝核工業(yè)西南物理研究院陳偉研究員和浙江大學仇志勇教授的討論.