巖溶區鐵路列車荷載對新建下穿隧道動力響應規律

杜碧濤,劉遠明*,陳會宇,陳慶芝,陳林全,滕召磊

(1.貴州大學土木工程學院,貴陽 550025; 2.貴州省巖土力學與工程安全重點實驗室,貴陽 550025;3.貴州省交通規劃勘察設計研究院股份有限公司,貴陽 550008)

隨著全國各地城市軌道交通建設如火如荼地進行,隧道下穿既有鐵路的工況發生得愈發頻繁,例如貴陽市軌道交通3號線一期工程下穿鐵路的工點就達3個之多。貴陽屬于喀斯特山地城市,巖溶極其發育,因此在諸如貴陽這種巖溶地區地鐵隧道施工穿越既有鐵路過程中極有可能遇見拱頂溶洞,若不采取相應防控措施,地表和路基在列車長期循環振動荷載作用下,會有塌陷的風險,該事故在巖溶地區已屢見不鮮[1]。在實際工程中,遇到溶洞一般是采用注漿的方式進行填充加固,而列車動荷載對隧道及地層的動力響應在溶洞處理前后勢必呈現不同的規律。

近幾年,學者們關于空洞對淺埋暗挖隧道施工的影響做了不少研究[2-6]。例如,蔡義等[3-4]通過三維模型試驗及FLAC3D數值模擬分析了隧道上方含空洞地層在地鐵隧道施工擾動下的變形規律。趙文強[5]同樣采用模型試驗與數值模擬結合的手段研究了隧道開挖擾動下含空洞地層失穩機制,提出“超前地質預報+注漿防治”的控制方法并通過后期監測證實了該方法的可靠性。邢志豪等[6]依托深圳地鐵16號線盾構隧道穿越巖溶溶洞工程,采用數值計算分析方法,重點研究了不同位置處溶洞注漿加固前后對地鐵盾構隧道穩定性的影響作用。與此同時,關于列車動荷載對新建下穿隧道影響的研究也不少[7-10]。高玄濤[11]與龔倫等[12]通過數值分析分別研究了單線與雙線列車運行對下伏隧道的影響,前者發現隧道施工至交疊處時,列車動載對隧道影響最不利;后者發現當對向行駛的兩列車機車的后轉向架輪載同時作用于隧道正上方時,為隧道結構的最不利位置。于鶴然等[13]研究了高速列車動荷載作用下立體交叉鐵路隧道位移、加速度、內力的響應規律。Xu等[14]采用模型試驗和數值模擬結合的方法,揭示了高架橋列車荷載作用下,樁土復合地基與相鄰隧道的動力響應特性。魏云峰等[15]通過數值模擬對列車移動荷載作用下運營隧道-加固區-地層的系統動力響應進行研究,并得出了不同列車運行速度對結構-地層系統各測點加速度、動應力和動位移的響應規律。晏啟祥等[16]設計了有、無橫通道的 2 種平行交叉的盾構隧道模型,研究了列車荷載作用下平行交叉盾構隧道的動力響應特征,弄清了聯絡橫通道對兩主隧道振動響應的影響機制。

可以看出,現有研究要么是關于溶洞及注漿加固后隧道在土層中開挖時的靜力影響,要么是關于在無缺陷均質地層中列車動載引起的動力響應,而在隧道下穿鐵路時列車動荷載作用下,拱頂存在溶洞及注漿加固對新建隧道動力響應規律影響的研究尚有欠缺。因此,現以貴陽軌道交通3號線地鐵隧道下穿川黔鐵路為背景,考慮最不利條件,采用列車動力計算中常用的有限元軟件Midas/GTS[17-21],建模計算分析隧道與既有鐵路交疊處存在隱伏溶洞時,對其處理前后,鐵路列車移動荷載對下穿隧道、地表及地層的動力響應的規律,以期為巖溶地區隧道下穿既有線工程提供參考。

1 工程背景

1.1 巖溶發育概況

貴陽市軌道交通3號線一期工程沿南北向縱貫貴陽市主城區,線路全長40.86 km,根據工程勘測資料,隧道沿線所處巖層主要以白云巖和石灰巖等可溶性碳酸鹽為主。據鉆孔揭露,巖層常見溶隙及溶洞,全線693個鉆孔中見溶洞的鉆孔75個,鉆孔見洞率為10.8%,溶洞直徑與埋深分布如圖1所示。

1.2 隧道下穿鐵路段概況

地鐵隧道于花果園西站—花果園東站某區段以69°斜下穿川黔鐵路,該鐵路為單線,屬于客貨共線鐵路,鐵路路基底距離隧道頂部豎向最小凈距約10 m。該區間隧道采用上下臺階法施工,隧道斷面形狀為6.52 m(寬)×7.17 m(高)的馬蹄形,初支采用0.26 m厚C25噴射混凝土和I18型鋼鋼架0.6 m/榀。整個下穿段隧道均處于風化石灰巖地層中。

2 數值模型建立

2.1 基礎三維模型

由于該區間隧道下穿段處埋深為10 m,從圖1的溶洞分布圖可以看出,埋深10 m以下溶洞有18個,占24%,且其中洞徑最大的為5 m。基于該實際工程背景,考慮最不利條件,建立隧道施工至與鐵路交疊處時,拱頂無溶洞、有直徑為5 m的溶洞和溶洞注漿加固3種工況的數值模型(溶洞位于拱頂與地表正中間),計算分析列車駛過時3種工況的動力響應規律。注漿加固材料采用水泥砂漿,同時考慮漿液的擴散效應,將注漿加固區域保守地劃分為厚度均為0.5 m的2部分,3種計算工況詳情如圖2所示。

圖2 3種不同計算工況

在巖溶地區,地層情況多為上部覆蓋較薄的土層,下部為可溶性風化巖層,為使該研究成果對不同工程也具有廣泛的借鑒參考價值,地基簡化采用巖溶區地質條件較差的強風化石灰巖。參照實際工程資料與相關規范[22],最終確定模型材料力學參數如表1所示。其中,軌枕與初期支護采用彈性本構模型,分別用實體與板單元模擬;其余各結構層次材料強度準則均采用各向同性的摩爾庫倫本構模型,用實體單元模擬。

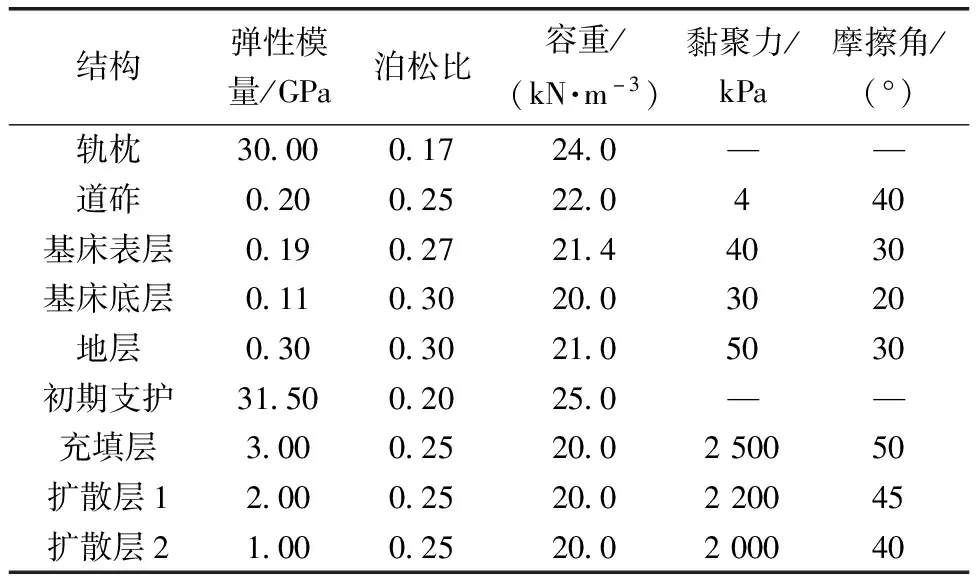
表1 模型材料參數

基于圣維南原理,取三維計算模型尺寸為:70 m(長)×50 m(寬)×50 m(高);鐵路路基相關幾何尺寸參照規范[22]取值:軌枕厚度為0.15 m,間距0.6 m;道砟厚度取0.3 m;基床表層與底層厚度分別為0.6 m、1.9 m。建立基礎三維模型如圖3所示。

2.2 特征值分析

在進行動力計算之前,需要對結構進行特征值分析獲得質量參與率最高的兩個模態周期,進而計算出結構的阻尼系數。根據式(1)和式(2)計算特征值分析的彈簧邊界值[23]。

豎向地基反力系數為

kv=kv0(Bv/30)-3/4

(1)

水平地基反力系數為

kh=kh0(Bh/30)-3/4

(2)

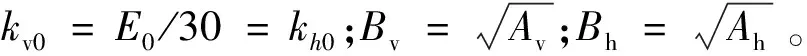
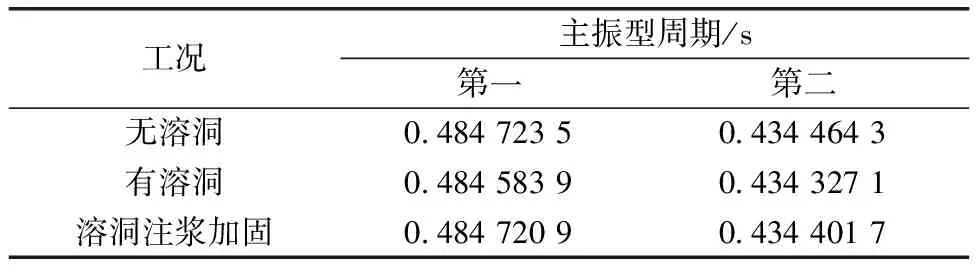
表2 3種工況主振型周期

2.3 動力計算模型

2.3.1 列車荷載模擬

在實際工程中,由于列車營運場地環境的復雜性,通過現場實測獲得列車動力荷載較為困難;因此,絕大多數研究對于動荷載的模擬都是采用國內外學者們根據現場試驗總結出的一些經驗分析方法。其中應用范圍最廣的是梁波等[24]提出的與高、中、低頻相應的,反映不平順、附加動荷和軌面波形磨耗效應的激勵力來模擬輪軌之間的相互作用力;后經充分考慮列車輪對力在線路上的移動,疊加組合與鋼軌、軌枕的分散傳遞因素,得到了作用在軌枕上用于模擬高速列車振動荷載的激振力函數[25]為

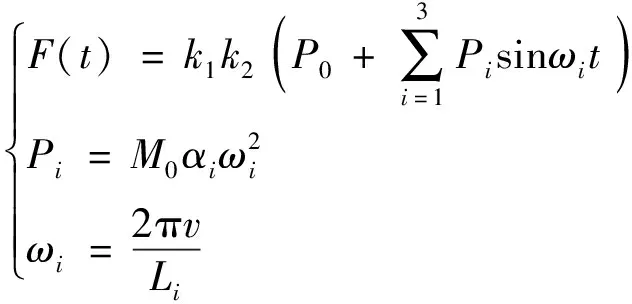
(3)

式(3)中:k1為相鄰輪軌力疊加系數;k2為鋼軌分散系數;P0為車輪靜載;i=1,2,3,分別對應低、中、高頻3種情況;Pi為振動荷載;M0為列車簧下質量;αi為軌道的幾何不平順矢高;ωi為不平順振動波長的角頻率;v為列車速度;Li為軌道不平順波長;t為時間。

列車行駛速度越大,列車荷載對鄰近建筑的動力響應也越大;因此,采用客貨共線鐵路最高設計時速v=200 km/h;k1、k2分別取1.6、0.8;取單輪靜載P0=80 kN,簧下質量M0=950 kg,低、中、高頻對應的典型不平順波長和矢高采用英國鐵路軌道不平順功率譜:L1=10 m,a1=3.5 mm,L2=2 m,a2=0.4 mm,L3=0.5 m,a3=0.08 mm;結合式(3)計算得到列車豎向荷載時程曲線如圖4所示。

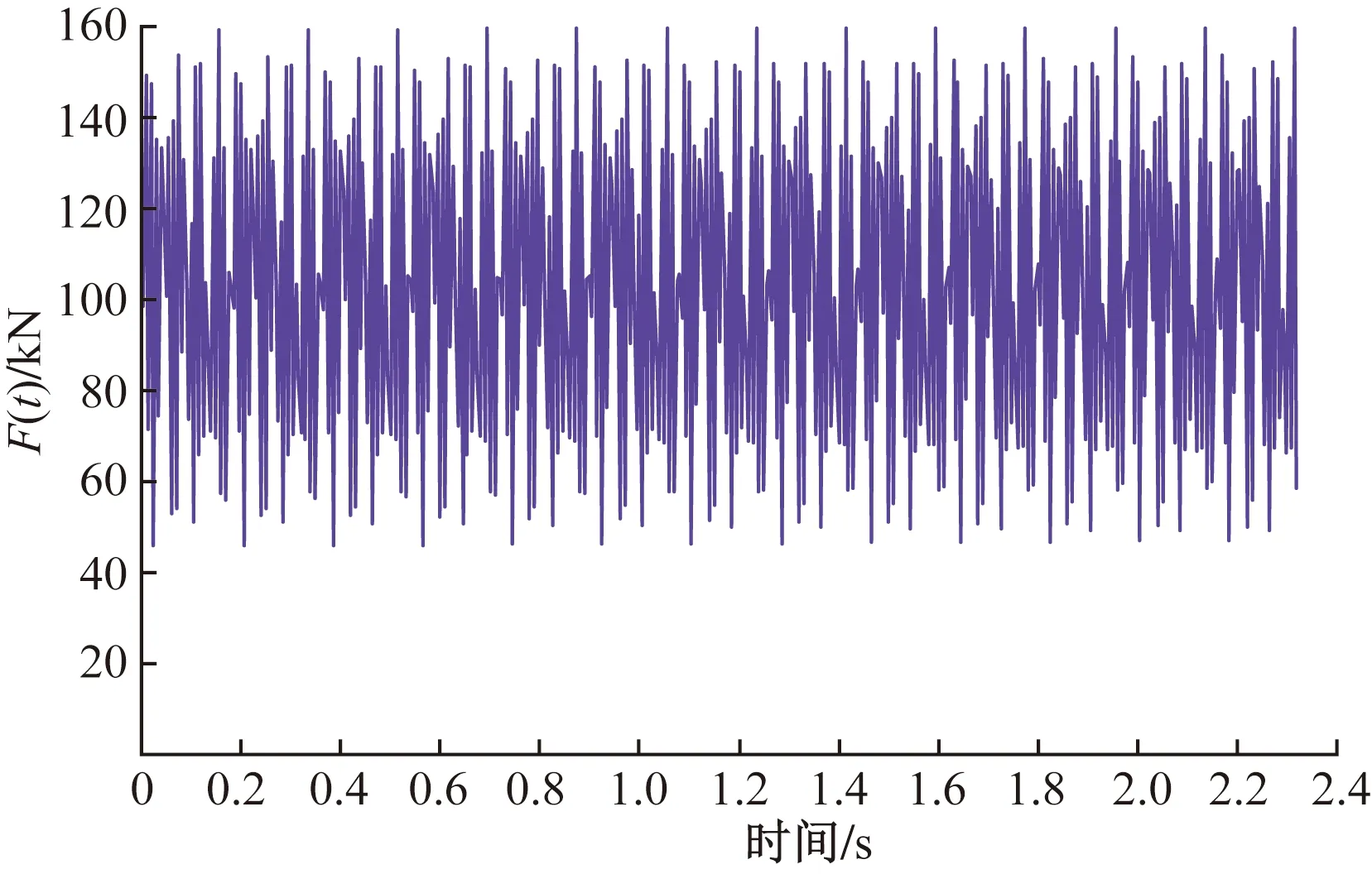
圖4 激振力時程曲線

2.3.2 列車荷載施加方式

列車動力荷載確定后,采用定點豎向加載的方式將荷載以固定的時間間隔依次施加在軌枕上,以模擬列車行駛過程,如圖5所示。本次模擬取列車長度為130 m,而列車時速是55.56 m/s,因此列車駛過一個軌枕的時間約為2.3 s(激振力作用時長);軌枕間距為0.6 m,故激振力施加于相鄰兩軌枕的間隔時間為0.010 8 s;該模型路基的長度為73.2 m,所以列車從進入到完全駛出模型邊界需要3.7 s。因此進行時程分析時,設置動力計算時間為4 s。為保證計算精度,隱式積分的時間步長不能大于模態分析中最高階振型周期的1/10,因此在此計算模型中取積分步長Δt=0.01 s。

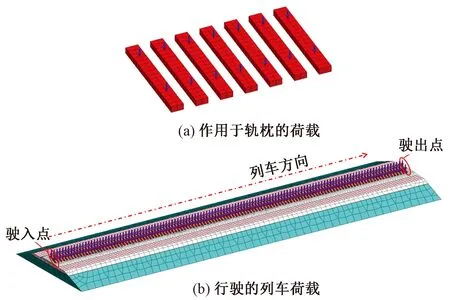
圖5 列車移動荷載布置

2.3.3 動力邊界條件

在進行動力理論或數值分析時,計算模型都是用有限區域代替無限區域。因此,為了合理地解決動力波在邊界上的反射問題,模型x、y方向設置黏性局部人工邊界,底部采用固定邊界。定義黏性邊界需要采用Lysmer等[26]提出的公式計算各結構材料的阻尼值。

P波阻尼系數為

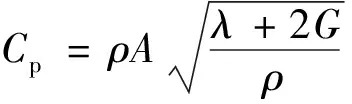
(4)

S波阻尼系數為

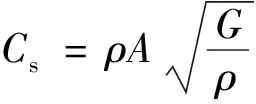
(5)

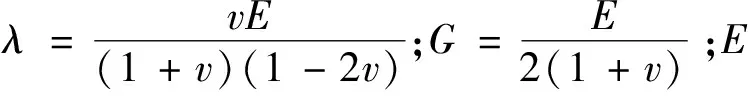
3 動力計算結果分析

3.1 分析內容與監測點布置

主要研究了在列車移動荷載作用下,交疊處隧道拱頂無溶洞、有溶洞及注漿加固3種工況下隧道結構的豎向動位移和最大主應力響應規律,地表的豎向動位移響應規律以及地層的動位移、動應力衰減規律。對研究目標的監測點布置如圖6所示,地表沿路基垂直方向布置4個測點,為了便于研究分析,使測點間距與溶洞直徑相近,同時要適應網格尺寸,因此取4個監測點距離隧道與路基中線交叉處分別為0.00、4.11、8.22、12.73 m。

3.2 隧道動位移響應分析

根據已有學者的研究,隧道施工至交疊處時,列車動載對隧道影響最不利[11]。因此當隧道開挖至交疊處時,在拱頂上方無溶洞、有溶洞與溶洞注漿加固3種工況模型中,分別施加激振力時程荷載模擬計算列車從駛入到駛出的完整過程,提取得到隧道拱頂的豎向動位移時程曲線如圖7所示。

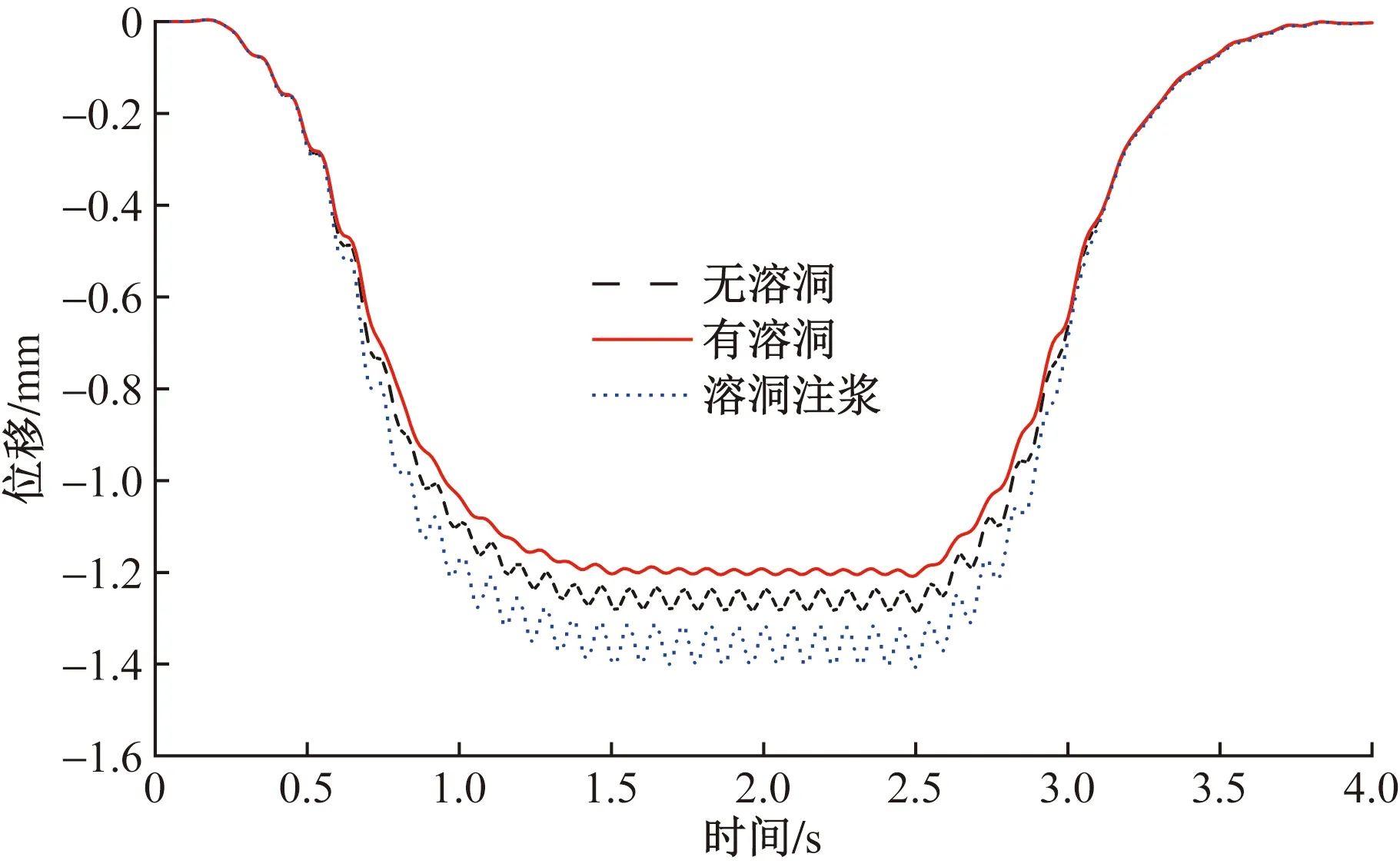
圖7 隧道拱頂豎向位移時程曲線

分析圖7可知,無論在哪種工況下,由于地層的阻尼特性對振動波傳播過程產生的滯后效應,拱頂在列車駛入模型邊界后約0.3 s才有位移響應,此后位移呈波動性逐漸增大;在列車完全駛入模型的時刻,即1.3 s后位移呈平穩波動趨勢;隨著列車行進,在2.3 s時車尾離開駛入點,同樣由于振動波傳播的滯后效應,拱頂豎向動位移在2.6 s后呈波動性逐漸衰減,直至列車完全駛出模型,在4 s時基本回彈恢復至零。這與張暢飛[27]采用FLAC3D計算分析上跨隧道中列車移動荷載作用下,下穿隧道拱頂的位移時程曲線具有一致的振動規律與趨勢。同時也將該曲線與Sekiya等[28]在地鐵運行時采用MEMS加速度計測得的隧道加速度數據進行兩次數學積分后得到的位移響應曲線進行了對比,由于兩者地質情況、隧道類型和列車時速不同,所以峰值大小有所差異,但同樣具有相同的振動規律,該數值模型計算結果與實際工程現場實測結果存在較高相似性,因此,本文研究對實際工程具有一定的理論指導意義和參考價值。

與此同時,列車荷載作用下隧道拱腰、拱腳和拱底豎向位移也具有與拱頂相同的振動響應規律,為了更直觀深入地研究分析,現將3種工況下隧道各監測點豎向動位移峰值變化情況如圖8所示。

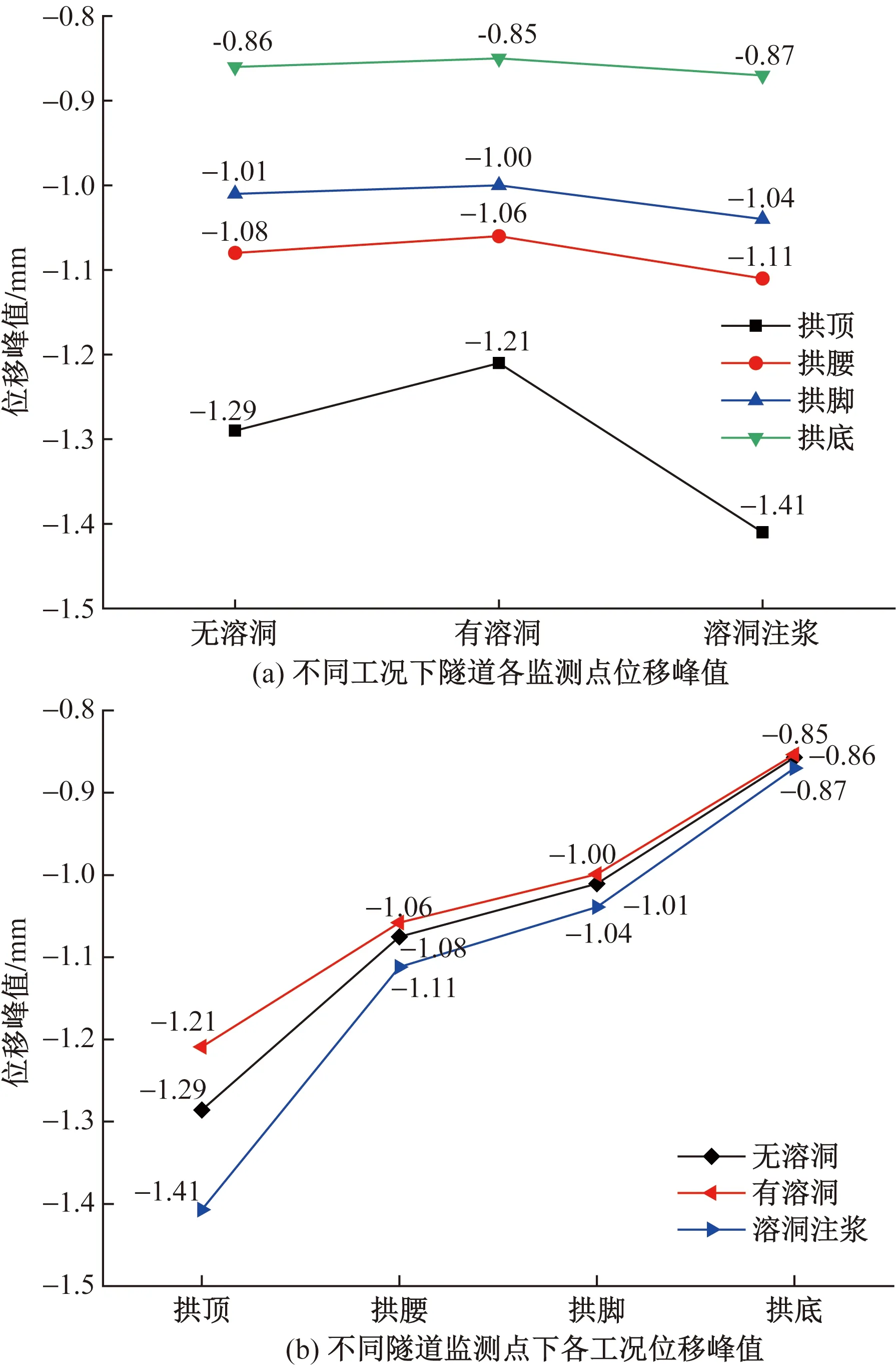
圖8 隧道監測點豎向位移峰值變化趨勢

綜合分析圖8可得如下結果。

(1)在列車動載作用下,隧道各監測點在不同工況下豎向動位移峰值大小排序均為:溶洞注漿>無溶洞>有溶洞;前者是由于注漿體的彈性模量比周圍地層更大,相對不容易發生壓縮變形,故將列車的豎向荷載更多地傳到了注漿體以下的地層,從而使隧道支護結構產生了更大的豎向位移;后者是由于臨空溶洞對動位移進行一定程度的釋放。

(2)無論何種工況,各監測點豎向動位移峰值大小排序均為:拱頂>拱腰>拱腳>拱底;同時,隧道各監測點動力響應受不同工況的影響程度也遵循該規律,溶洞的存在及對其注漿對拱頂的影響相對顯著,但對拱底的影響卻比較微弱;顯然這都是由于振動波在地層中傳播時隨著深度增加而逐漸衰減的緣故。

(3)隧道最大位移峰值發生在溶洞注漿工況下的拱頂位置,為-1.41 mm,相較于無溶洞和有溶洞工況分別增大了9.3%、16.5%,但即便如此,該位移仍遠未達到一般隧道拱頂沉降控制標準。

3.3 地表動位移響應分析

在3種不同工況下分別施加列車移動荷載,得到地表監測點1豎向動位移時程曲線如圖9所示。

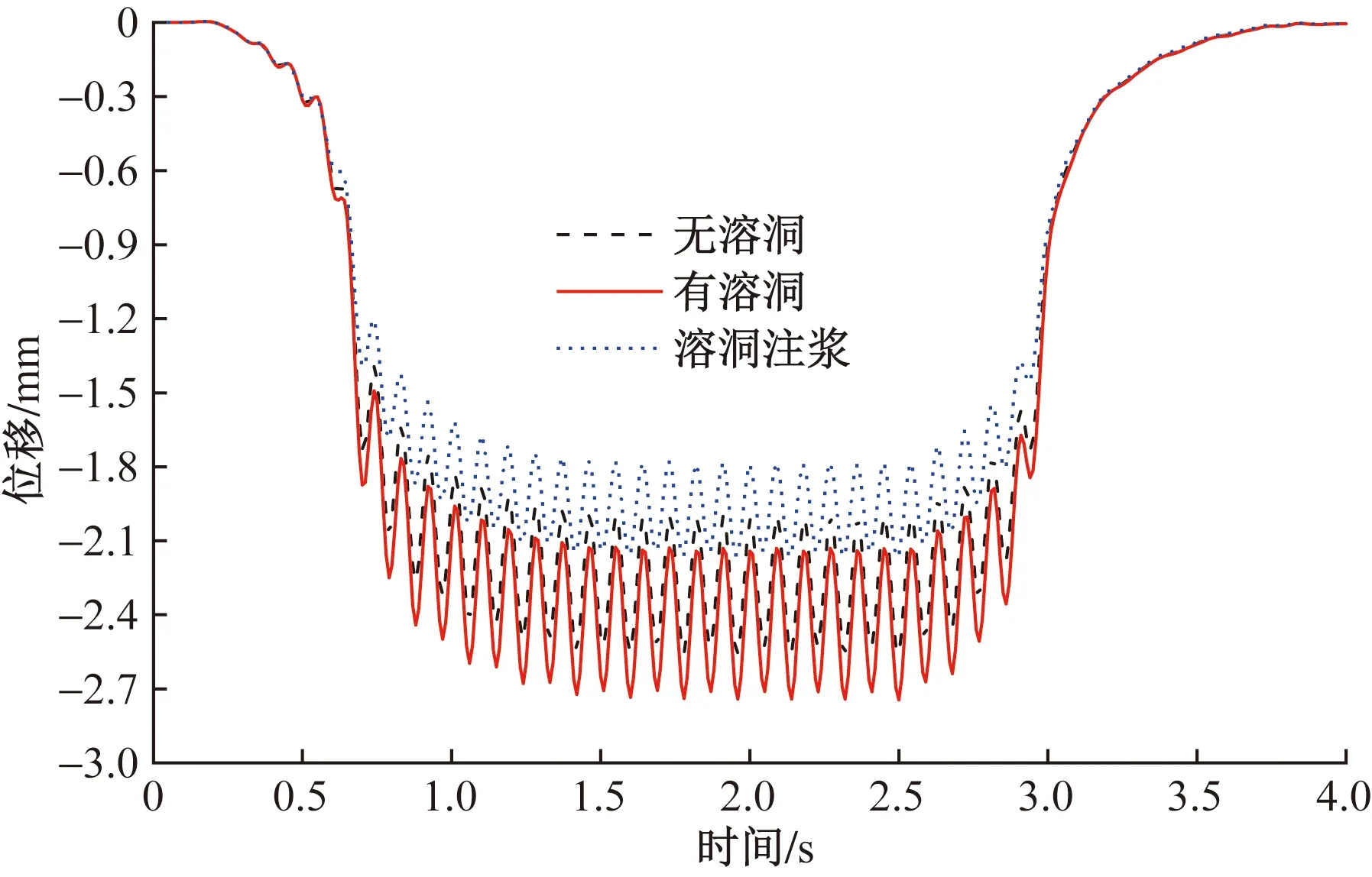
圖9 地表監測點1豎向位移時程曲線

不出所料,由于振動波還未經過地層阻尼的衰減,與隧道動位移相比,地表的動位移無論是波動幅度還是峰值都明顯更大;為了研究不同工況下位移振動沿地表橫向衰減的規律,將地表各監測點的豎向動位移峰值變化情況如圖10所示。

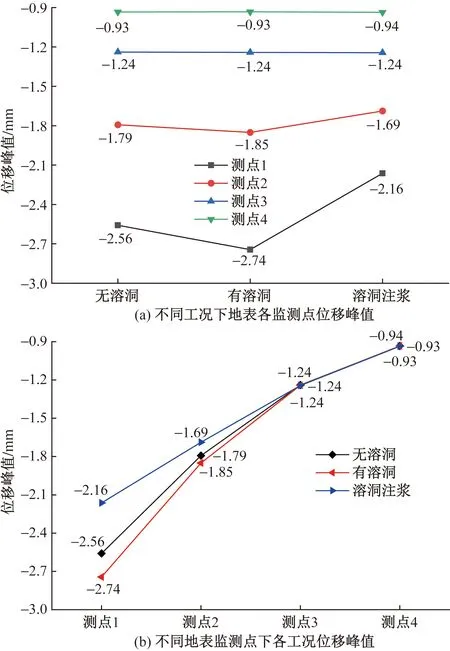
圖10 地表監測點豎向位移峰值變化趨勢

綜合分析圖10可得如下結果。

(1)當計算結果保留兩位小數時,從圖10中可以看出距離交疊處較近的地表監測點1和監測點2受溶洞的存在及對其注漿的影響相對較大,3種工況下位移峰值大小排序為:有溶洞>無溶洞>溶洞注漿,而測點3和測點4幾乎不受影響;由此可知在列車荷載作用下,溶洞的存在及對其注漿對地表動力響應的影響范圍大致為3.3倍洞徑以內(8.22×2/5≈3.3)。

(2)地表最大位移峰值發生在有溶洞工況下的測點1位置(路基中線與隧道中線交叉處),為2.74 mm,而無溶洞和溶洞注漿工況在此監測點的位移分別減小了6.6%、21.2%;由此可見,溶洞的注漿加固可以明顯改善降低列車動荷載引起的地表瞬時沉降峰值。

3.4 隧道最大主應力響應分析

由于混凝土結構的抗拉強度遠小于其抗壓強度,而最大主應力更接近于拉應力,故將初期支護的最大主應力響應也納入研究范圍。隧道各監測點最大主應力時程曲線如圖11所示。

由圖11分析可知,在列車動荷載作用下,隧道在不同工況下同一監測點處的最大主應力時程曲線都具有相同的振動規律,并且拱頂和拱底主要處于受拉振動狀態(正值為拉),而拱腰和拱腳則主要處于受壓振動狀態。為詳細分析不同工況對隧道受力狀態的影響規律,將各監測點的最大主應力峰值變化情況繪于圖12所示。

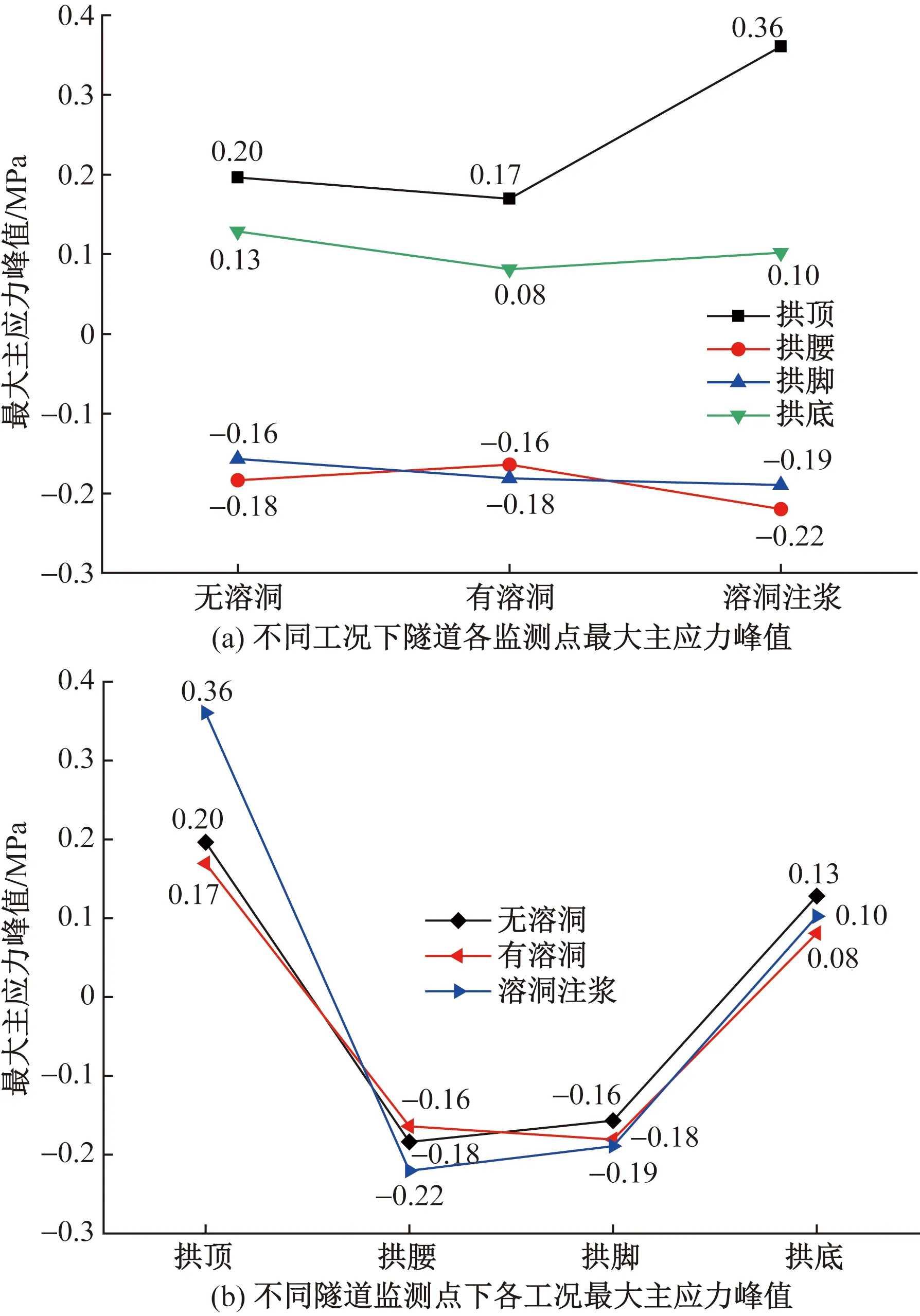
圖12 隧道監測點最大主應力峰值變化趨勢

綜合分析圖12可得如下結果。

(1)相較于無溶洞而言,溶洞的存在使振動波在地層的傳播削減后,隧道拱頂、拱腰和拱底的最大主應力峰值均有所減小;而溶洞注漿則使隧道拱頂、拱腰和拱腳的最大主應力峰值均有所增大。

(2)無論何種工況下,隧道拱頂和拱底的最大主應力峰值均為正,處于不利的受拉狀態,并且拱頂所受的拉應力總比拱底大;而拱腰和拱腳的最大主應力峰值均為負值,處于受壓狀態。

(3)溶洞注漿工況下的隧道拱頂是最不利受力點位,最大主應力峰值為-0.36 MPa,遠小于C25混凝土的極限抗拉強度1.78 MPa,因此列車動載作用下隧道結構是安全的。

3.5 地層動應力衰減分析

如圖13所示,列車通過時不同工況下地表監測點1的豎向應力也呈有規律的波動狀態。為詳細分析地層豎向應力的變化情況,將3種工況下監測點1和隧道拱頂的豎向應力峰值列于表3所示。

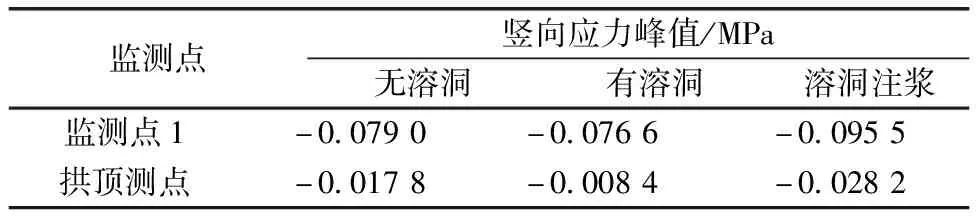
表3 地層不同監測點豎向應力峰值

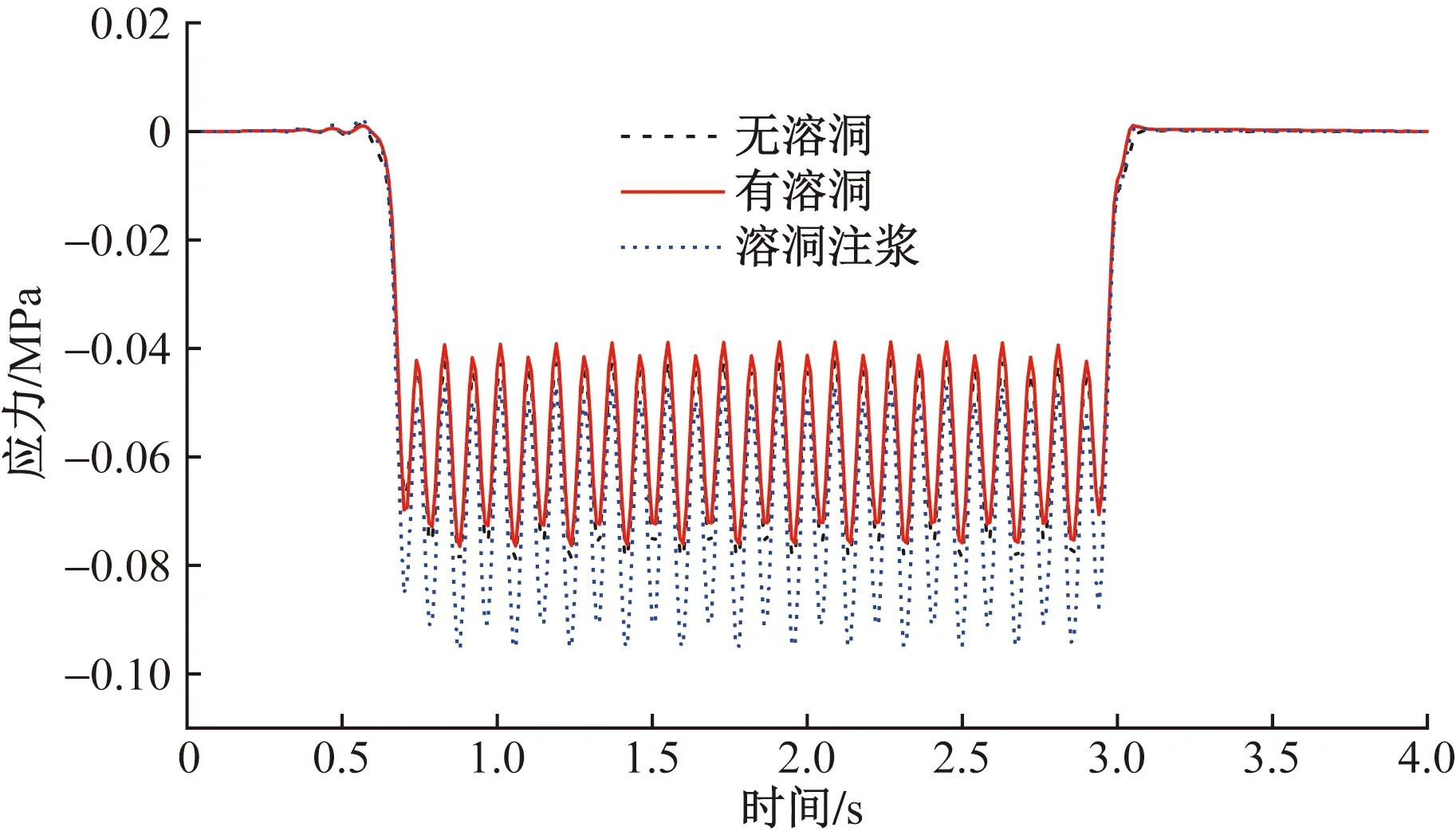
圖13 地表監測點1應力時程曲線

根據處于不同地層深度兩監測點的應力峰值可以看出,無論哪種工況都不會改變列車動載引起的應力響應隨地層深度衰減的現象。其中,衰減最明顯的是有溶洞存在的情況,從-0.076 6 MPa 衰減到-0.008 4 MPa,衰減率為89.03%;無溶洞和溶洞注漿兩種工況的地層應力衰減率分別是77.47%、70.47%,相對較小,這就直觀解釋了溶洞注漿加固后地表的動位移響應得到減小,而隧道動位移響應有所增大的現象。

4 結論

以貴陽軌道交通3號線的實際工程背景為依托,研究了在巖溶地層新建地鐵隧道下穿既有鐵路過程中,時速為200 km/h的列車振動荷載對隧道、地表及地層的位移和應力響應規律。得出如下結論。

(1)溶洞的存在和對其注漿加固并不會改變列車振動荷載引起隧道、地表及地層的位移和應力動力響應的時程規律,均是呈有規則的波動狀態,最后逐漸回彈恢復。

(2)溶洞存在及對其注漿加固對地表位移動力響應的影響范圍大致為3.3倍洞徑以內;對地層溶洞注漿加固后使地表最大瞬時沉降減小了21.2%,可以有效降低列車荷載在長期循環作用下地表振動塌陷的風險。

(3)由于振動波在地層中傳播時會隨深度增加而逐漸衰減,因此在3種工況中,隧道各監測點豎向動位移峰值大小和動位移響應受不同工況的影響程度遵循的規律為:拱頂>拱腰>拱腳>拱底。列車動載作用下,隧道拱頂和拱底處于不利的受拉狀態,且拱頂所受的拉應力總比拱底大;而拱腰和拱腳則處于受壓狀態。

(4)由于溶洞注漿加固減小了地層應力的衰減,因此使得隧道在外部列車動載作用下產生了相對大的動力響應,但均遠小于一般隧道拱頂沉降控制值和C25混凝土的極限抗拉強度,是滿足安全標準的;為了同時達到控制地表沉降和保證隧道安全的目的,建議選擇與地層彈性模量接近的注漿材料最佳。