改進小波閾值函數在手部姿態獲取中的應用*

徐晗昕，俞斌杰，柳 麗，3，王 英，3，杜森浩

（1.寧波大學機械工程與力學學院，浙江 寧波 315211；2.浙江智馬達智能科技有限公司，浙江 寧波 315336；3.浙江省零件軋制成型技術研究重點實驗室，浙江 寧波 315211）

0 引 言

手在人們日常生活中起著重要的作用，手功能障礙患者及時進行有效的康復訓練對加快恢復有著十分重要的影響［1］。然而康復訓練周期長，多次往返醫院的經濟、時間成本高，因此，迫切需要對手部康復訓練裝置及系統進行設計與開發，讓手部康復訓練智能化、便捷化。

手部康復系統中，手部姿態獲取方式主要有機器視覺和數據手套等。楊文璐等人［2］、Lapiana N 等人［3］、Xue Y等人［4］利用機器視覺于康復系統中，但該方式容易受到光線、遮擋等因素影響，且要求使用系統的患者手部須一直放置在攝像頭能夠拍攝到的范圍內。龔文等人［5］、趙裕沛等人［6］、Wang D等人［7］設計了力反饋數據手套，利用傳感器采集手部運動姿態信息，具有普適性。然而，由于微加工技術與集成工藝技術的限制和使用過程中外界環境多變等因素，使得傳感器輸出信號檢測不準確。如何高效降噪，提高傳感器輸出信號的精度這一難題亟待解決。

廣受青睞的小波變換法由于獨特的多分辨率特性能夠更好地分解非平穩信號，有效濾除噪聲干擾［8］。小波變換常用的方法包括模數最大法、系數相關法和閾值降噪法，其中，小波閾值法降噪具有計算速度快、信號保留完整等特點，得到了廣泛應用。

由Donoho教授于1995年提出的著名硬、軟閾值函數，其優點主要表現為易于實現，運算簡單，且變換后能夠降低熵值，但實踐應用中該方法仍然存在不足和缺陷［9］。硬閾值函數能較好地保留信號的局部邊緣特征，但在閾值處不連續，會導致小波重構時出現較為明顯的振蕩。軟閾值函數彌補了硬閾值函數在閾值處不連續問題，但其處理的小波估計系數與信號的小波系數之間存在固定偏差，使得部分信號丟失，影響了小波重構后原始信號的還原度。為此，研究人員采取了很多方法進行閾值函數的改進。Fong J等人［10］提出一種利用粒子群優化算法調整參數的改進小波閾值函數，并結合貝葉斯收縮閾值法重構小波系數；孫然然［11］提出CALE 閾值函數，通過在不同的分解層數設置不同的閾值使得閾值處具有連貫性；趙薇等人［12］提出一種雙參數閾值函數，通過加入調節參數使得改進的閾值函數能在硬閾值與軟閾值函數之間切換；甘若等人［13］提出將閾值函數與對數函數相結合解決傳統閾值函數不連續、失真等問題；田江龍等人［14］基于改進硬閾值法和雙變量小波閾值函數的方法使去噪后的信號在過分平滑與邊緣振蕩現象之間達到合理的平衡。以上改進策略中，或引入了多個暫定參數加大了計算量，或函數過于復雜加大了計算難度，降低了傳感器數據輸出的實時性。李朋等人［15］提出將閾值函數閾值內部分的小波系數從置零改為一定數值解決在閾值處間斷的問題，但仍不可避免會保留一部分噪聲。

針對手部康復系統對真實手與虛擬手運動同步性及精準性要求，本文基于極限的思想提出一種改進小波閾值函數，在不額外添加調節參數的前提下，解決傳統閾值函數不連續、失真等問題，使去噪信號無限逼近與原始信號，同時保證傳感器數據傳輸的穩定性、實時性。

1 小波閾值去噪原理

首先采用Mallat塔式算法逐層分解計算帶噪的小波變換系數，如圖1。分解后信號的小波系數（Cd）大于噪聲的小波系數（Ca），然后通過設定的閾值分離兩種系數，保留大于閾值的信號小波系數，置零小于閾值的噪聲小波系數，從而達到去噪的目的。小波閾值去噪基本流程如下：首先，通過選擇合適的層數和小波基對噪聲信號進行分解，得到小波系數wj，k；其次，選擇合適的閾值，利用閾值函數對各層系數進行量化，得到小波估計系數＾wi，j；最后，通過重構小波估計系數得到去噪后的信號。

圖1 小波變換示意

2 改進小波閾值函數

2.1 改進閾值函數推導

本文提出一種改進的小波閾值函數，表達式為

式中λ為閾值，wj，k為分解后得到j層第k個小波系數，為wj，k估計的小波系數。

該閾值函數具有以下特點：

1）連續性：

當wj，k→λ時

可知，改進閾值函數在wj，k→λ時是連續的。

同理，當wj，k→-λ時

可知，改進閾值函數在wj，k→-λ時是連續的。

因此，改進閾值函數在閾值處是連續的。

2）漸進性：

當wj，k→+∞時

同理，當wj，k→-∞時

因此，使用本文構造的改進閾值函數處理后的小波估計系數無限逼近于處理前的小波系數，減小了恒定偏差。

改進閾值函數與兩種傳統閾值函數圖像對比如圖2所示。

圖2 改進閾值函數、軟／硬閾值函數對比

2.2 改進閾值函數仿真與分析

本文通過仿真軟件設計了一個原始信號并且添加高斯白噪聲進行仿真。原始信號及含噪信號的表達式如下

式中 NoiseSignal（t）為含噪信號，Signal（t）為原始信號，GaussianNoise（t）為高斯白噪聲，Coe為噪聲的比例系數。

原始信號公式中，前面一段模擬了姿態傳感器靜止不動的情況，后面兩段模擬姿態傳感器運動時候的情況。原始信號和含噪信號如圖3所示。

圖3 仿真信號

對于含噪仿真信號分別用傳統的軟硬閾值函數和改進閾值函數進行去噪分析，其中小波基選取去噪效果較好且具有更好的正則性與對稱性的SymN 函數，分解層數為5層，去噪閾值選擇為固定閾值。處理后的數據如圖4 所示。從圖4 中可以看出，改進閾值函數去噪效果在信號整體平滑度和精度上都有明顯提升。

圖4 去噪效果對比

信號去噪效果評估通常采用信噪比（SNR）與均方根誤差（RMSE）來量化分析［16～18］。SNR和RMSE的定義為

式中Psig為不含噪聲原始信號的功率，PN為噪聲的功率，Nsig為含噪信號，sig為不含噪聲的原始信號，N為信號的長度。

對3種閾值函數處理后的數據分別計算信噪比與均方根誤差，結果如表1 所示。由表1 可以看出，3 種閾值函數處理后的信噪比，相比未處理前都有明顯提高，其中改進閾值函數提升效果最好；均方根誤差也是改進閾值函數處理后的數值更小。仿真結果表明，本文提出的改進閾值函數能夠在保留原始信號特征的基礎上，有效抑制重構信號振蕩。

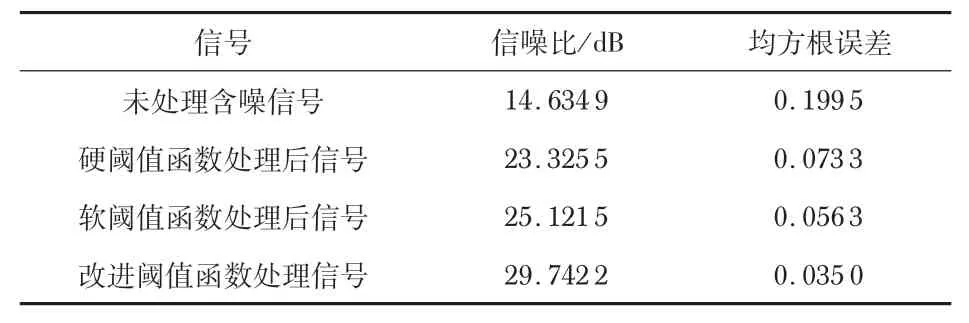
表1 降噪效果對比

3 實驗驗證

3.1 實驗方案

由于仿真信號添加的噪聲較為單一，而實際工作環境所含有的噪聲較為復雜且無規律［19］，現通過將改進閾值函數應用于手部康復系統中以進一步驗證其去噪能力。

如圖5所示，所設計的手部康復系統主要由數據手套、數據采集模塊、控制模塊、上位機、交互軟件等部分組成，針對處于康復中后期手指關節已經有了一定的力量與靈敏度的患者可協助進行靈敏度訓練［20］。患手穿戴手套訓練時，首先模擬抓取小球，然后手腕翻轉一定角度將小球拋出來鍛煉手指、手腕的關節活動度。傳感器采集患者手部運動姿態、手指彎曲度等數據傳輸給控制模塊，通過串口發送給上位機。上位機中交互軟件解碼傳感器數據控制虛擬場景變化，實現真實手與交互軟件中虛擬手的運動映射，進行小球抓／拋運動的可視化。同時，系統記錄訓練數據，為醫生指導患者訓練提供客觀依據。

圖5 實驗方案設計

3.2 系統搭建與實現

本文手部康復系統所使用的數據手套如圖6 所示。數據采集模塊采用Jy61 姿態傳感器和Flex2.2 彎曲度傳感器，控制模塊采用Arduino開發板。上位機系統硬件配置為Intel?CoreTMi7-8700處理器，CPU 主頻為3.2 GHz，運行內存4 GB，顯卡為NVIDIA GeForce GT730。交互軟件系統采用Windows 10平臺，利用Unity 3D搭建手部靈敏度康復訓練場景，模型構建使用3Dmax。開發語言為C＃，主要用于算法編寫，并實現系統與數據手套的串口通信。

圖6 數據手套

為測試改進閾值函數去噪效果的有效性，在完成康復系統調試后，測試者穿戴數據手套，與場景中虛擬手進行交互，通過真實人手模擬抓拋球運動，帶動虛擬手抓拋場景中的虛擬小球，如圖7。

測試實驗發現，虛擬手對真實手動作同步性良好，無明顯延遲，并且動作平穩順暢，基本避免了虛擬手因環境噪聲產生的抖動。實驗結果表明：本文構造的改進小波閾值函數可有效消除手部姿態獲取過程中的噪聲并與實際特征數據相契合。

4 結束語

本文提出了一種改進小波閾值函數，在不額外添加調節參數的前提下，解決傳統閾值函數不連續、失真等問題。通過仿真軟件對添加高斯白噪聲的數據信號進行去噪，結果表明：改進閾值函數去噪效果更佳，其信噪比和均方根誤差相比軟硬閾值函數都有明顯的優勢，均方誤差小，峰值信噪比大。

將改進閾值函數搭載在手部康復系統的數據手套上，對姿態傳感器（Jy61模塊）信號進行去噪實驗，驗證了方法的有效性。算法可有效提高手部姿態、手指彎曲度等信息獲取精度，以及系統映射的實時性，具有良好的實際應用價值。