電動汽車充電站選址智能決策與優化研究綜述

魏冠元，王冠群，阮觀梅，耿 娜

1.國網能源研究院有限公司，北京 102209

2.上海交通大學 中美物流研究院，上海 200030

近十年來，汽車數量快速增長，環境污染和能源短缺問題日益凸顯。據我國公安部統計，截至2022年6月底，全國汽車保有量高達3.10億輛[1]，比2012年增加近2倍。在此背景下，具有低碳環保、經濟高效等特點的EV受到了廣泛關注和重視[2]。然而，EV 續航里程短、充電設施不足等制約了其產業的發展[3]。對此，國務院辦公廳印發了《新能源汽車產業發展規劃（2021—2035年）》，指出要加快充換電基礎設施建設，科學布局充換電基礎設施[4]。作為EV 運行的關鍵保障，充電站的科學選址布局不僅對促進EV 的普及有重要作用，還有利于提高充電站相關企業的盈利水平以及用戶滿意度。而充電站不合理的選址也會帶來系列問題，如影響城市交通網絡的規劃布局等[5]。因此，對EV 充電站選址進行深入研究具有重要意義。

在20 世紀90 年代，一些學者主要基于經典選址方法對EV充電站選址布局展開研究[6-7]。隨著EV電池等相關技術不斷成熟，以及在政府政策推動下，越來越多學者深入研究EV 充電站選址問題，涌現出許多新內容和新方法。而目前關于EV充電站選址的研究綜述相對較少[8-10]，為全面觀察充電站選址研究的發展情況，本文選取近20 年CNKI 數據庫以及Web of Science 數據庫的相關文獻，對EV充電站選址問題展開系統綜述，分別從充電站選址基本原則和影響因素、充電需求估計方法、充電站選址模型和求解方法等系統梳理EV 充電站選址智能決策和優化的相關文獻，整體邏輯框架見圖1。最后總結現有研究存在的不足并對未來研究方向進行了展望，對今后關于EV 充電站選址智能決策與優化的相關研究提供參考和借鑒。

1 充電站選址基本原則和影響因素研究

1.1 EV充電站選址基本原則

選址基本原則是EV 充電站合理布局的重要標準指南。

（1）經濟性原則。在進行EV充電站布局規劃時，從運營商角度，需要盡可能選擇土地成本低、電力成本經濟、交通費用小、運行維護消耗少等投資運營成本最小的充電站布局[11]；從用戶角度，需要考慮繞行距離、出行時間和損耗成本最小；從社會角度，應綜合考慮充電公司和用戶成本最小化[12]。

（2）便利性原則。EV 充電站選址應考慮用戶異質性需求，并滿足充電站服務半徑需求，即服務半徑小于EV的續駛里程[13]。此外，應避免在車流速快、車道多的區域設置充電站[14]。

（3）可行性原則。EV 充電站選址主要涉及地理環境和社會環境的建設可行性。充電站選址應盡可能避免防洪條件差、地震多發的區域[14]；且應符合地區電網和路網規劃相關要求[15]。

（4）安全性原則。EV 充電站選址不僅要考慮最大負荷需求，滿足大規模EV電力需要，保障電網運行的安全性[16]，還應充分考慮防火防爆等安全需求，避免靠近容易發生火災或爆炸的危險區域[15]。

1.2 EV充電站選址影響因素

EV 充電站選址是一個復雜的過程，厘清充電站選址的影響因素是準確進行選址決策的重要前提。

宏觀層面，充電站選址影響因素主要包括經濟因素、政策因素、社會因素、環境因素和技術因素。其一，由于商業性質，EV充電站選址有必要考慮土地成本[17]、投資成本[18]、損耗成本[19]、運營維護成本[20]等經濟因素。其二，EV充電站的選址布局離不開國家、地區各類政策的引導與支持。政府作為第四方投資者，對所選地區建設充電站實施的政策主要包括規范文件、補貼政策、電價優惠和稅收優惠等[21]。不同地區的政策差異較大，需要對所選地區政策具體分析后再進行選址。其三，社會因素決定了EV 充電站選址能否滿足更多居民的需求，提高居民滿意度[22]。影響充電站選址的社會因素主要包括人口密度[23]、居民態度[24]、社會福利[25]等。同時道路情況、交通流量等交通環境對充電站選址具有重要影響[26]。Raveendran 等[27]認為充電站可以布局在機場、地鐵車站、校園、辦公大樓等區域。而Capar等[28]指出只有道路網絡的節點才能被視為候選選址。此外，技術因素是EV 充電站選址的重要支撐，主要考慮相關技術下電網容量、電能質量等能否滿足EV的充電需求[29-30]。由于充電站與配電系統相連，其選址布局時需要考慮配電系統的容量大小、電壓上下限值等[2]。而當大規模EV 接入配電系統時，會引起節點電壓嚴重下降，從而對其他用戶用電造成影響[31]，因此充電站選址時需要考慮提高電能質量的相關技術因素，如無功補償技術等。

微觀層面，充電站選址影響因素主要包括充電需求和供給因素。EV充電需求是影響充電站選址布局的關鍵因素[13]，主要包括充電需求量和需求類型。一方面，區域的充電需求總量主要與該區EV保有量、行駛里程、區域經濟水平、人口密度有關[32]；用戶充電需求量取決于用戶充電行為特征，如出行頻率、出行距離、充電選擇偏好、排隊時間接受度等[10]。另一方面，充電需求分為慢充需求、常規充電需求和快充需求三種類型，一般選擇在住宅區和辦公室停車場建立慢速充電站，在商業停車場建立額定功率相對較高的常規充電站，在道路沿線建立快速充電站[33]。充電站選址還應綜合考慮充電需求的時空分布特征，例如充電高峰和低峰時間段的比例分布[34]。胡培婷等[35]指出廣州充電需求高度集聚，應選擇緊湊型的充電站布局。此外，充電站在進行選址時需要對服務能力、服務時間、充電站可達性等供給能力進行分析，以匹配充電需求。大型充電站應具備為各類EV充電的能力，中型充電站則須具備為多種常見EV充電的能力[36]。服務時間主要受到EV 運行模式的影響。例如由于公交車和公務車晚間停運，因此可在其停運時間開放充電服務，利用電力低谷進行常規充電[13]。充電站可達性受服務半徑影響。較大的服務半徑雖然使得充電站數量減少，投資成本降低，但是可達性同時也降低，用戶體驗下降[32]。

2 EV充電需求估計方法

2.1 基于出行模擬的充電需求估計

較多研究采用基于概率統計的蒙特卡洛模擬（Monte Carlo simulation，MCS）方法估計充電需求，即通過模擬EV 出行時間、出行路線及隨機充電行為等，估計EV 充電需求時間、地點和功率。基于概率統計的蒙特卡洛模擬方法總結如表1所示。

早期學者主要研究充電模式、時間和地點固定的情形，利用MCS 抽取EV 起始荷電狀態（state of charge，SOC）來計算充電負荷需求。羅卓偉等[37]指出商場、超市停車場等地點存在充電時長限制，而單位和居民停車場則允許長時間充電，因此針對前者假設起始充電時間范圍給定，針對后者則假設EV充滿電才離開，分析了不同充電模式下EV充電需求，但是對起始SOC等參數選取具有一定主觀性。同時該種確定性概率分布的模擬方法難以反映現實中EV充電行為的隨機性特征。

部分學者進一步考慮了EV 出行的多樣性和隨機性。與常規概率模型假設EV 接入電網后立即充電不同，周念成等[38]針對混合動力EV 改進了初始SOC 的抽樣方法，考慮充電時間長度對開始充電時刻選擇的影響，同時引入隨機因素如EV實時充電數量，構建多種類型EV 接入配電網的充電需求概率模擬模型。然而，該類研究缺少對出行和停放地點、道路交通等空間因素的考慮，忽視了不同區域EV 的時空分布特性對充電需求的影響。

近年來，有關EV 充電需求的研究重點從需求時間分布預測發展到時空分布預測。許威等[39]基于馬爾可夫鏈描述EV 一天出行過程中荷電狀態的變化情況，考慮交通擁堵對行駛時間的影響，利用MCS 對用戶行為規律進行精細化模擬，能夠較好地體現工作區、住宅區、商業區等不同區域的EV 充電負荷曲線，但是對用戶行為考慮不夠充分。對此，鮑瓊等[40]構建用戶出行-充電行為鏈，結合模糊邏輯刻畫用戶充電行為，使用MCS模擬用戶群體的出行和充電行為，能夠將時間分布預測精確到分鐘，空間需求預測精確到路網節點，但是沒有考慮用戶群體與其行為模式異質性的影響。而Zhang等[41]通過MCS模擬各地區EV到達狀態，并將用戶分為緊急用戶和隨機用戶，其中緊急用戶必定選擇充電，而隨機用戶則根據模糊推理算法估計充電概率，針對不同用戶建立分層充電決策模型，再根據決策結果進行充電需求估計。該研究很好地解決了實際情況中不同用戶如何做出充電決策，以及不同決策下需求的時空分布問題，但是缺乏真實的EV軌跡數據支撐。

綜上，基于概率統計的MCS 方法優勢在于所需數據量較少，通過模擬用戶出行規律，能夠獲得EV充電需求的時空分布特征。但是隨著EV 的普及，該方法存在明顯局限性。一方面，由于充電需求影響因素較多且關系復雜，難以獲得準確的概率模型[42]。另一方面，該方法主要基于模擬數據進行需求預測，缺乏真實數據支撐，難以反映現實充電需求的真實情況[43]。

2.2 基于數據分析的充電需求估計

數據分析方法主要通過挖掘EV真實的歷史運行數據，分析EV 出行和充電行為的規律，進而估計充電需求。基于數據分析的充電需求估計方法如表2所示。

早期由于缺乏實際數據，許多學者基于社會人口特征、EV 保有量和交通流量等統計數據直接估計充電需求[44]。He 等[45]從《北京統計年鑒》和《全國人口普查》中選取了六個關鍵的社會人口特征，包括收入、車輛擁有量、教育水平、年齡、性別和家庭規模，并通過德爾菲法確定權重，將六個特征進行加權得到充電需求，其中人口普查數據比較老舊，且樣本量小。Luo 等[46]基于河南省私家車保有量、全國EV保有量和全國私家車保有量，采用灰色預測模型預測河南省EV保有量，以此衡量EV充電需求總量，大大削弱了EV 保有量預測的隨機性程度，提高了穩定性。王輝等[47]通過重力空間互動模型求得EV交通流量，并使用交通流量模擬EV充電需求，重力空間互動模型比較直觀且解釋性強，但是沒有考慮用戶行為，且當距離較小時，可能會夸大預測。

隨著EV 運行數據的積累和可獲得性，部分學者基于軌跡數據進行充電需求估計。不同于以統計數據估計的充電需求僅在地理單位上表示，基于軌跡數據的充電需求還涉及時間維度，通常表達為單位時間到達率。例如，Yang 等[48]基于一周長沙電動出租車GPS 數據，提取停靠站數，將每日平均停靠站數作為每日到達率即充電需求，但是沒有考慮SOC的影響，同時缺少對電動出租車以外的EV 的數據挖掘和充電需求研究。羅思杰等[49]深入分析了電動出租車的出行特征和停留偏好，根據出租車軌跡大數據挖掘出租車就餐、交接班、上洗手間等短暫非運營時間，并以非運營時間作為充電需求時間，該研究綜合考慮了用戶充電的便利性以及充電站經濟性，但是由于假設EV在多個地點停車，使得需求估計準確性不高。這些研究均沒有考慮用戶異質性的影響，而周椿奇等[50]分別針對電動私家車用戶和電動運營車用戶，通過開源數據平臺提供的EV出行軌跡數據，并根據微觀能耗模型，估計不同時間序列的EV充電需求，獲得了EV 充電需求的精確定位，缺點在于開源數據和規模有限。

隨著大數據時代的到來，近兩年許多學者基于數據驅動的方法智能估計充電需求。Zhang等[51]基于北京3個月25 489輛EV的大量運行數據，從時間、空間和能量多維度提取EV 的行為特征，基于高斯混合模型和Kmeans 的兩步聚類模型，將用戶分為具有不同使用習慣、屬性和特征的6 種類型，進一步建立基于出行鏈模擬的充電需求預測模型，實現了對實際充電需求的高精度預測，但缺少對不同地區和季節充電需求的分析。Yi等[52]基于兩個地區不同規模的真實數據，使用深度學習-序列到序列方法對每月EV 充電需求進行了長期預測，有效考慮了充電站屬性以及數據中的時間相關性，但由于需求數據按月匯總，導致訓練數據減少，使得該模型較一般機器學習模型和時間序列模型優越性不大。如果數據能具體到每個充電站的每日需求，則在海量數據支撐下，基于數據驅動的智能估計方法將表現出更優的充電需求預測精度。

綜上，統計數據獲取相對容易，但這些數據大多以年為周期，缺乏時效性，且不區分EV 類型，忽略了EV特點。軌跡數據通常使用調查數據或GPS數據，更能真實反映用戶真實出行情況，提高預測效果，但是許多研究使用燃油汽車的軌跡數據代替EV 軌跡數據，不能真實反映充電需求。基于數據驅動的智能估計方法能夠實現更高精度的充電需求預測，但前提是具備海量的詳細數據。

3 EV充電站選址模型與求解

3.1 基于不同需求的充電站選址模型

根據不同EV 充電需求的表達方式，可將充電站選址模型分為兩類基于點需求的選址模型、基于起訖點（origin-destination，OD）對流量需求的選址模型和基于軌跡的選址模型。

3.1.1 基于點需求的選址模型

基于點需求的選址模型假設需求發生在固定節點上（如住宅、辦公場所等），目前主要分為3種基本模型：P-中值模型（P-median），P-中心模型（P-center）和覆蓋模型（covering location model），如表3所示。

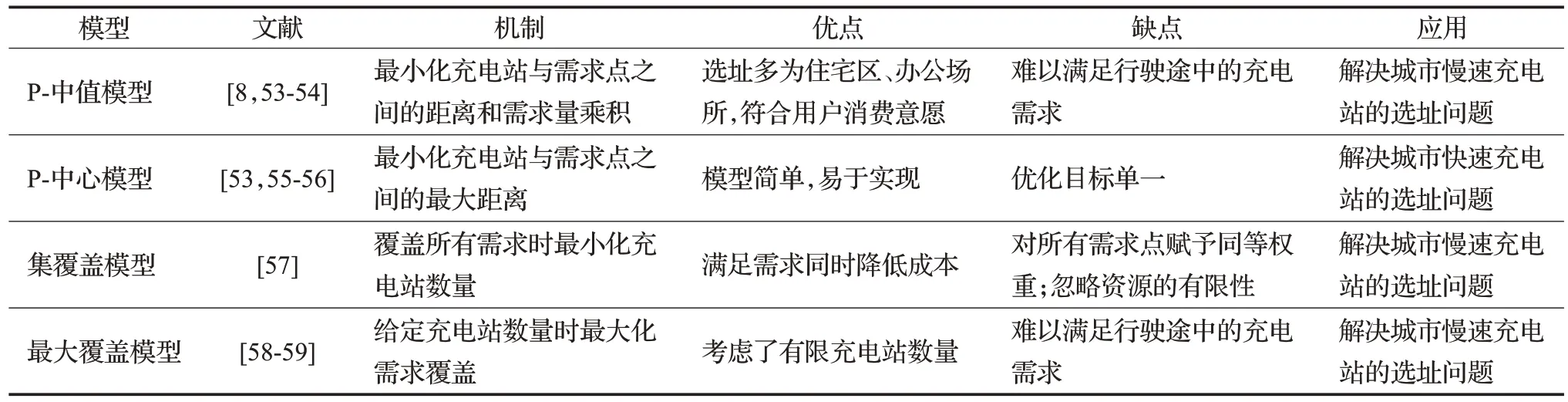
表3 基于點需求的選址模型Table 3 Location models of EV charging station based on point demand

P-中值模型由Hakimi[53]首次提出，即研究如何在給定候選位置下為P個充電站進行選址決策，使得充電站與需求點之間的距離和需求量乘積最小。不同于傳統P-中值模型，孫秉珍等[54]考慮了充電需求不確定性的影響，構建"預選址-增建選址"兩階段多目標區間P-中值模型，得到的充電站選址最優方案降低了充電中斷后的各項運營成本，但是該模型相對簡單，對影響需求的其他影響因素考慮較少。P-中值模型優點是選址通常發生在住宅或辦公場所，比較符合用戶消費意愿[8]，但是充電需求不僅發生在住宅和辦公場所，還可能發生在路上；該方法適用于城市環境的選址問題。

經典P-中值模型表示如下：

式中，i和j分別為需求點和充電站候選點的集合；hi為第i個需求點的需求量；dij為第i個需求點到第j個充電站之間的距離；yij=1 表示充電站j能滿足i點的需求，否則為0；xj=1 表示在第j點建立充電站，否則為0；P為建立充電站的數量。

P-中心模型旨在最小化充電站與需求點之間的最大距離[53]。賈龍等[55]考慮不同充電站間的相互影響，提出了改進的P-中心模型，令所有充電站與需求點之間距離與充電需求大小的乘積之和最小，有效滿足城市不同類型EV的充電需求，但是沒有考慮EV行駛路徑、充電偏好和道路擁堵等因素的影響。P-中心模型優點是易于實現，但是優化目標單一；該方法適用于需要緊急服務的設施選址問題[56]。

覆蓋模型又可以分為集覆蓋模型（set covering）和最大覆蓋模型（maximum covering）兩類。集覆蓋模型旨在覆蓋所有需求點時使得充電站建設成本和充電站數量最小。Wang 等[57]基于集合覆蓋和車輛加油思想，使用混合整數規劃方法確定充電站選址，以滿足城內和城市間的最大充電需求，同時最大限度地降低成本。集合覆蓋模型的局限性在于對所有需求點賦予同等權重，并且忽略了資源的有限性。于是Church 等[58]提出最大覆蓋模型，在有限充電站數量和服務半徑基礎上盡可能覆蓋較多的需求點。Hamed 等[59]基于最大覆蓋模型研究了不同充電場景下的選址問題，創新性引入隨機參數方法估計白天和黑夜的預期充電功率需求，然而所采用的用戶出行模式、汽車保有量等數據不是真實數據而是估計得來，容易受到其他因素如地區就業水平的影響，進而影響充電站數量和選址。

經典最大覆蓋模型表示如下：

式中，i和j分別為需求點和充電站候選點的集合；hi為第i個需求點的需求量；λi=1 表示i點的需求能被充電站在R距離內覆蓋，否則為0；xj=1 表示在第j點建立充電站，否則為0；P為建立充電站的數量。

綜上，基于點需求的選址模型主要適用于城市充電站的選址規劃。優點在于模型比較簡單，僅需有限的數據，是早期研究中常用的經典方法。但是該方法通常假設用戶不會距離固定的充電站位置太遠[60]，無法解決長途出行時EV有限行駛里程下的選址問題。

3.1.2 基于OD對流量需求的選址模型

基于OD 對流量需求的選址模相比于基于點需求的選址模型可能更符合現實情況，假設用戶可能在從出發地到目的地路程中的任何一點充電。基于OD 對流量需求的選址模型中充電需求由OD對替代，包括起末位點、路徑以及線路上的交通流量，交通流量往往由沿著該OD 對出行的行程數量表示。相關選址模型總結如表4所示。

表4 基于OD對流量需求的選址模型Table 4 Location models of EV charging station based on OD pair flow demand

Hodgson[6]于1990年首次提出了著名的截流選址模型（flow-capturing location model，FCLM），旨在需求路徑和充電站數量給定的情況下，通過選址使得截取的需求量最大。FCLM模型認為在OD對所在的路程中建立單個站點可以截取路徑的全部需求量，然而現實中單個充電站服務范圍是有限的，EV 可能在途中耗盡電量。對此，不同學者對FCLM模型進行了改進。Kuby等[61]進一步結合汽車行駛里程約束，提出了帶有能源補充的選址模型（flow-refueling location model，FRLM）。Liu等[62]基于FRLM 模型研究了高速公路網上的充電站選址，考慮了充電站數量約束、用戶充電選擇行為和里程焦慮等供需因素的影響，并通過沿路段增加充電站候選位置來擴展模型，但是該研究沒有考慮偏離路徑需求以及充電站容量的影響。實際上，用戶通常會因為需要充電而偏離原來的路徑，因此上述模型假設用戶沿著最短路徑到達充電站存在明顯局限性。

經典FCLM模型表示如下：

式中，fq為第q條路徑上的交通流量；λq=1 表示在第q條路徑上至少建一個充電站，否則為0；xj=1 表示在第j點建立充電站，否則為0；P為建立充電站的數量；NP為截取需求量的節點集合；N為所有節點的集合。

Kim等[63]不僅考慮行駛里程約束，同時還考慮繞行最短的情況，提出了偏離需求路徑的選址模型（deviationflow refueling location model，DFRLM），提高了覆蓋需求預測的準確性。偏離衰減函數和最大允許偏離的選擇對最優選址有重要影響，需要對偏離行為進行仔細建模，但會增加問題的復雜性和求解難度。Xu 等[64]首次開發了考慮路徑偏離的緊湊模型，并將非線性的里程焦慮特征納入EV 充電站選址的決策中，通過外逼近法求解，計算效率不高。

另外，Wu等[65]針對充電需求的不確定性，建立了隨機截流選址模型（stochastic flow-capturing location model，SFCLM），發現當充電站數量有限時，SFCLM 模型優于確定性模型，隨著充電站數量增加，SFCLM模型和確定性模型選址方案愈相似；但該研究沒有考慮不同區域EV具有不同滲透率，而是直接給定滲透率。

綜上，由于充電需求發生在EV 行駛途中，基于OD對流量需求的選址模型適合快速充電站的選址規劃。優點在于更細致地考慮了用戶出行特征，但是所需數據獲取較難，且很少考慮充電站的容量限制。

3.1.3 基于軌跡的選址模型

EV 尤其電動出租車在長時間、長距離行駛過程中可能需要進行多次充電，而在行駛途中建立多個充電站顯然不符合實際。對此一些學者提出了基于軌跡的選址模型，即根據含有多個OD對的行程鏈而不僅是單個OD行程進行充電站選址。相關研究總結如表5所示。

表5 基于軌跡的選址模型Table 5 Location models of EV charging station based on EV trajectory

Jung等[66]建立了隨機動態行程攔截選址模型，考慮了傳統選址模型欠缺的一些特征，如排隊時延、每輛電動出租車均根據隨機動態行程運行，且在每段行程結束后才產生充電需求。但是該模型結果缺乏空間公平，即出租車較多考慮在充電站附近的客戶。與Jung 等[66]基于交通規劃軟件合成隨機需求數據不同，Tu等[67]從現實中大量的GPS 數據中提取汽車軌跡和乘客需求的實際信息來構建時空需求覆蓋選址模型，基于用戶角度，最大化EV 總行駛距離和減少充電等待時間；該研究突破了以往大部分研究僅考慮空間問題的局限性，但是僅適用于電動出租車，且忽略了乘車需求的可變性，即客戶可能轉向地鐵或公交服務。

經典隨機動態行程攔截選址模型將問題定義為雙層規劃問題，模型表示如下：

上層：

式中，Ci( )S為最接近節點i的節點集合；λi為單位時間需求產生率，由下層問題求得；u為服務率；dij為i節點到j節點的行駛成本；Wki為在有k個充電站的節點上花費的期望時間；S為候選點集合；ki=1 表示在第i點建立充電站；P為建立充電站的數量；Dq,i為排隊時延。

Keawthong 等[68]基于曼谷出租車的GPS 軌跡數據，同時考慮了排隊時延和出行時間的影響，提出一種確定充電器數量和選址的分析工作流程；并通過真實反映曼谷交通情況的谷歌地圖距離矩陣API數據進行驗證，發現該方法能夠有效減少出租車到充電站的出行時間和排隊等待時間，但是數據成本和計算成本較高。

綜上，基于軌跡的選址模型同樣適用于城市中快速充電站的選址規劃。優點在于能夠綜合考慮EV軌跡信息和乘客需求信息，對充電需求時空分布進行深入分析，得到更加符合現實的選址方案。KO 等[69]指出如果具備詳細的車輛活動時空數據，則基于軌跡的選址模型比其他模型更具有潛力。但是該方法主要面向電動出租車，且海量數據較難獲得。

3.2 充電站選址模型求解方法

針對上述充電站選址模型，根據求解方法，可以分為精確算法、啟發式算法和深度學習算法。

3.2.1 精確算法

用于解決充電站選址問題的精確算法主要包括分支定界算法、分支切割算法、Bender 分解等。相關方法總結如表6所示。

表6 精確算法Table 6 Exact algorithms

分支定界算法是求解選址問題的經典方法[70]。該方法關鍵是確定目標上界和下界，通過在搜索過程中剪掉相關分支，從而提高搜索效率，適用于求解成本最小等單目標優化問題。Bao等[71]發現當EV行駛里程相對較低時，分支定界算法可以快速獲得全局最優，但是如果增加行駛里程，則計算時間會大幅增加。孫智勇等[72]結合降階子算法設計分支定界算法，縮小了問題的規模，進而加快求解基于最小開設費用的充電站選址問題。

分支切割算法在分支定界算法的基礎上，加入割平面來收緊線性松弛。Yildiz等[73]采用分支切割算法求解了同時考慮隨機充電需求、充電站容量限制和駕駛員的路線偏好的充電站選址問題，指出分支切割算法能夠有效處理具有大量場景和充電需求的大型問題實例，但是按照充電次數對充電需求分組時會顯著增加需求，嚴重影響計算效率。

Benders分解算法主要通過將復雜規劃問題分解為非線性和線性子問題來求解，適用于包含復雜特征如多種類型EV、偏離路徑的充電站選址問題。Kadri等[74]基于Benders分解算法對需求不確定下快速充電站選址的多階段隨機問題進行求解，指出Benders 分解算法的性能明顯優于獨立的數學規劃求解器，但是難以解決考慮充電站容量約束和擁堵的選址問題。

盡管精確算法能夠求得全局最優解，Kizhakkan等[75]指出精確算法需要對輸入數據進行預處理，以得到最短路徑、可行組、OD 對等，需要耗費大量時間。因此許多學者傾向于采用啟發式算法，雖然求解結果通常為局部最優解，但是求解速度較快。

3.2.2 啟發式算法

現有文獻主要通過遺傳算法、粒子群優化算法、免疫算法、貪婪算法、禁忌搜索和模擬退火等啟發式算法對充電站選址模型進行求解。相關方法總結如表7所示。

表7 啟發式算法Table 7 Heuristic algorithms

遺傳算法通過模擬自然進化過程來搜索最優解，在解決選址問題中得到廣泛應用。Zhou 等[76]運用遺傳算法求解了基于社會總成本的充電站選址模型，其中總成本包括建筑成本、運營成本、環境成本等；指出由于遺傳算法基于概率規則而不是確定性規則，搜索比較靈活，減小了參數對其搜索效果的影響，但是該算法效率通常較低，并且可能會出現過早收斂的問題。Zhang 等[77]提出一種改進的遺傳算法，利用適應度值、記憶和轉移優秀基因改變交叉率，避免過早收斂問題。與以往優化單一目標的遺傳算法不同，Zhang 等[78]提出了一種混合非支配排序遺傳算法，以解決充電站選址和用戶分配的多目標雙層規劃問題，缺點在于假設用戶偏好一致，因為多樣性偏好可能導致算法計算效率下降。總之，遺傳算法收斂速度相對較慢，但是能夠通過交叉變異或融合其他算法進行改進，很好地解決EV充電站選址規劃問題。粒子群優化算法是另一種常用于充電站選址問題的群體智能優化算法。汪和平等[79]通過改進粒子群算法對EV 快慢充電站選址進行優化，其中改進了慣性權重因子和縮放因子，引入變異概率和精英選擇策略，加快了收斂速度，并避免陷入局部最優，但是求解速度較慢。Muthukannan等[80]將粒子群優化算法與直接搜索法相結合，前者用來求解需求覆蓋最大化、總功率損耗和電壓偏差最小化的充電站選址優化問題，后者負責提高收斂性和準確性。總之，粒子群優化算法收斂速度快，但容易陷入局部搜索，現有關于充電站選址的研究主要通過改進粒子群算法或將其與其他算法融合，應用于多目標優化問題。

在其他算法方面，Zhang 等[81]將單點交叉兩點交叉相結合，并利用可變交叉率和突變率改進免疫算法，優化換電站選址問題，展現出更高的全局搜索能力和計算效率。免疫算法適用于多目標優化問題，孫秉珍等[54]驗證了免疫算法在求解多目標充電站選址問題時具有比傳統遺傳算法更高的優越性。Sun等[82]將考慮用戶滿意度的充電站選址問題視為單調子模最大化問題，用近似比證明了貪婪算法在求解大規模問題的適應性。何瑞輝等[83]通過禁忌搜索算法求解EV隨機行駛范圍下的充電站選址問題，在短時間內能夠獲得高質量的解。禁忌搜索算法收斂速度快，通過引入禁忌列表可以避免陷入局部優化[62]。肖白等[84]將模擬退火算法與迪克斯特拉算法結合，能夠有效地解決多約束條件下復雜非線性和強耦合性的充電站選址定容雙層規劃問題，有較強的全局尋優能力。

綜上，啟發式算法不需要預先生成組合，能夠在合適時間內解決復雜的選址問題。上述啟發式算法在收斂速度、全局搜索能力方面各有不同，通過混合應用，能夠取長補短，更好地解決EV充電站選址問題。

3.2.3 深度學習算法

隨著人工智能的發展，深度學習算法被逐漸應用于EV充電站選址。深度學習最早是由Hinton等[85]對人工神經網絡的研究中提出的。常用于解決選址問題的深度學習算法包括循環神經網絡、生成對抗網絡、深度強化學習等經典算法。相關方法總結如表8所示。

表8 深度學習算法Table 8 Deep learning algorithms

循環神經網絡呈樹狀結構，各網絡節點根據相應的輸入信息依次遞歸。循環神經網絡具有較強的學習能力，對數據的容忍度極強，能夠接受不連續的信息，同時在處理時間序列數據方面具有很強的優勢，但是該算法結構相對簡單，在面對更復雜的數據時容易陷入局部最優解，難以用單一的循環神經網絡算法對復雜的充電站選址問題進行研究。因此，Su[86]提出了一種集成螢火蟲算法的循環神經網絡算法，提高了全局優化能力，實現有效的充電站選址和定容目的。

生成對抗網絡算法通過對抗訓練過程構建生成模型。為了降低數據采集難度和模型構建所需的工作量，Wang 等[87]提出了條件生成對抗網絡算法，該算法能夠提取隱含信息，自動學習現有EV 充電站建設方案中的規則，并制定一個網絡模型，該模型可以根據輸入圖像輸出充電站建設位置。但是生成對抗網絡算法存在納什均衡有時得不到、訓練不穩定和模型崩潰的問題。

深度強化學習算法融合了深度學習和強化學習，提高了決策能力。Zhang 等[88]將EV 充電站規劃問題轉化為馬爾科夫決策過程，再利用深度強化學習算法解決該問題，實現了最小化EV總充電時間，并最大限度地縮短OD距離。深度強化學習算法具有較強的自適應能力和自我調節能力，能夠在環境的反饋中自動尋找最優策略，彌補了傳統啟發式算法復雜度高、泛化性差等不足，更適用于大規模地理空間數據背景下的充電站選址問題[89]。但是該算法要求樣本量大，訓練時間長，并且收斂性很容易受到參數影響。

其他深度學習算法，如卷積神經網絡、長短期記憶神經網絡等算法主要用于預測充電站需求而不是解決充電站選址問題[90-91]。

綜上，深度學習算法具有更出色的泛化和學習能力，能夠有效解決現實中復雜的充電站選址問題，但是所需數據規模大，訓練時間長，而且模型不穩定。

4 總結與展望

經過幾十年發展，現有關于EV 充電站選址的研究取得了很大進展。本文通過對這些研究進行梳理和歸納，分別對EV充電站選址基本原則和影響因素、充電需求估計方法、充電站選址模型和求解方法進行了系統介紹。發現這些研究在充電需求刻畫、模型構建方面仍存在一些不足。最后，結合理論與實際情況，指出了EV充電站選址的未來研究方向。

4.1 現有研究不足

（1）對充電需求刻畫不充分

影響因素方面，現有充電站選址模型大多忽略了EV充電技術、信息共享的影響。隨著充電技術的進步，EV的續航里程隨之擴大，充電需求也發生變化，當前最優選址在未來可能不是最優的，因此有必要考慮技術的影響。信息共享如告知充電等待時間和充電速度等對EV用戶充電需求產生重要影響，用戶可能會規避排隊，這取決于共享信息的頻率和精度，然而目前少有研究考慮信息共享這一因素。

充電需求估計方面，真實的充電需求涉及空間和時間維度，需要考慮隨機性和可變性，尤其在時間維度上需要從穩態均衡建模轉變為納入靈活的到達和服務過程。但既往研究通常將時間維度上的充電需求刻畫為每小時到達率，對充電站單日時刻上EV等待充電、離開等行為刻畫不充分。另外，既往研究通常將不同地區的全天充電功率需求刻畫為固定參數，很少考慮白天和夜間充電功率需求的顯著差異，對充電需求的無偏估計結果產生影響。

數據獲取方面，由于EV行業正處在發展階段，能夠獲得的真實駕駛數據較少，一些研究采用的燃油汽車數據不能準確刻畫用戶出行特征與充電需求的關系，尚需進一步挖掘EV軌跡數據并深入分析EV充電需求的時空分布。

（2）對充電站選址模型的目標考慮不全面

目標函數方面，在現有充電站選址模型中，大多數模型的最終目標旨在確定充電站的位置。然而充電站選址規劃除了確定最優位置，還需要考慮服務類型、容量選擇等問題。而且由于厘清EV充電需求是進行充電站選址的關鍵，目前充電站選址模型主要從用戶視角出發。面對當前EV充電站利用率低、盈利難等問題，需要綜合考慮用戶和運營方利益，權衡覆蓋范圍、成本和服務質量等多個目標。

約束條件方面，現有研究大多考慮充電站數量約束、充電站容量、交通條件約束、服務半徑約束等，很少考慮電網約束。大規模EV 充電可能會導致功率損耗、電壓驟降等電網問題，因此有必要考慮電網約束。但是現有研究很少考慮電網約束，尤其鮮有同時考慮電網和交通約束[92]。

4.2 未來展望

當前，EV 充電站在不同經濟發展水平的地區分布存在差異，導致空間不公平（spatial inequity）問題，影響EV 在不同收入群體間的普及率。如何量化EV 充電站布局的差異性和不公平性，分析其影響因素，在不同城市合理選擇充電站的位置和密度，實現有針對性的基礎設施投資，是未來研究的重要方向之一。

隨著信息技術的發展，EV 尋樁、充電更加智能化。EV充電站選址的未來研究有必要考慮智能交通系統和智能電網協同、車輛到電網技術（vehicle to grid）、可再生能源技術等。此外，相比于短期內建設充電站，考慮用戶偏好、等待時間的多周期動態選址可能更具現實意義。

現有研究大多采用遺傳算法、粒子群優化算法及其混合算法等求解選址問題，而隨著充電站選址問題復雜性的增加，設計更高效的求解算法成為未來關注重點。可以進一步考慮新型的啟發式算法、人工智能技術等。人工智能技術能夠實現充電站選址模型特征的獨立選擇，并解決模型演繹能力不足的問題，為涉及用戶、運營商和政府等多主體博弈的充電站選址復雜問題提供有效解決方法。