網絡畫板在初中數學教學中的應用

陳琪

摘 要：初中數學教學可以借助網絡畫板來開發資源，形成豐富的教學活動.本文就北師大版九年級上冊第一章《特殊平行四邊形》中的新授課、章節復習課、習題課的中相應課例應用網絡畫板進行繪制動態幾何，促進學生的幾何直觀和推理能力的發展，并形成網絡共享文件以期為初中數學教學提供一定的參考.

關鍵詞：初中數學；網絡畫板；特殊平行四邊形；幾何直觀

《義務教育數學課程標準（2022年版）》（下文簡稱課標）指出要促進信息技術與數學課程融合，以豐富的學習資源、生動的教學活動促進數學教學方式方法的變革^［1］.信息技術輔助數學教學活動是現在數學課堂中教師廣泛采用的手段，特別注意的是，信息技術要深入到學科之中，并結合學科特征進行設計并給予相應支持，否則就難以取得實際的教育教學效果^［2］.而網絡畫板是一款基于網頁操作的動態畫圖軟件，在如今網絡發達的情況下其方便性好、操作更加快捷，在培養學生數學幾何直觀的核心素養中具有推助力作用.

1 網絡畫板簡述

網絡畫板是在超級畫板的基礎上，為適應互聯網、移動互聯網環境下教育信息化發展的新趨勢，運用國內領先的動態幾何技術、智能推理技術、符號運算、網絡交互技術開發的第一款國內領先的移動互聯網環境下的動態數學學科教學工具.其具有免安裝、跨終端、跨平臺的特點^［3］.網絡畫板可以實現動態展示幾何圖形，并且智能畫筆功能強大，包含點、線、圓以及幾何的特殊關系的繪制；通過參數的設置，可以實現動態演示，如一次函數的一次項系數為可變參數，當參數變化時，一次函數圖象發生改變.當然，網絡畫板的功能不僅于此，網絡畫板網頁配備有學習資源以及共享資源，可以通過網絡視頻的學習進行網絡畫板操作，同樣可以通過他人共享的資源中作者的作圖步驟進行學習.總之，強大的網絡互通造就網絡畫板其應用性與便捷性.

目前希沃白板5.0課件提供網絡畫板輔助教學，形成互聯網下技術豐富、學生高度參與的智慧課堂環境^［4］.特別地，網絡畫板具有資源共享的功能，教師或其他用戶在完成創作時若呈現為共享形式，則其他人可以借助該資源進行學習或者幫助授課，是集眾數學教育者的智慧于一體的便攜式網頁輔助數學工具.

2 網絡畫板在初中數學課堂應用意義

《特殊平行四邊形》該章節是北師大版數學九年級上冊第一章的內容，承接八年級平行四邊形的性質與判定以及七年級簡單的平面圖形相關知識的學習，體現數學知識的螺旋式上升.初中數學強調在直觀理解和掌握圖形與幾何基本事實的基礎上，經歷得到和驗證數學結論的過程，感悟具有傳遞性的數學邏輯，形成幾何直觀和推理能力^［5］.利用網絡畫板輔助教學，形象的動畫演示、具體直觀的測量、充滿探究的拖拽變換等功能，可以使學生參與到數學探究活動中，幫助學生更好地理解幾何圖形中的定理，體會知識的本質，構建知識體系，進而提升學生的觀察聯想、類比學習的能力，進而發展數學幾何直觀和推理能力.

3 網絡畫板在初中教學中的應用例析

3.1 網絡畫板在新授課中的應用——“矩形的判定”

北師大教材中《矩形的性質與判定》關于“矩形的判定”內容部分涉及“平行四邊形活動框架”，該部分設計指出可以通過直觀教具引導學生進行對矩形的判定定理的猜想.

教材中在導入矩形的判定時，采用平行四邊形活動框架進行觀察，該活動在向學生展示四邊形不穩定性的同時，學生注意到平行四邊形的其中一個內角的變化，從而發現對角線長度以及平行四邊形的形狀也在發生變化.教師的教學設計意圖即著落于通過直觀教具的演示而引導學生得到一個猜想：對角線相等的平行四邊形是矩形.事實上，在整個教學過程中，除了教具的新舊會影響整個演示過程，學生實際參與度也缺乏.應用網絡畫板的技術則可以規避這些缺陷，同時其便捷以及資源共享的性質使得教師在自我動手創作時也可以就地取材——甄選其他教師共享的資源進行教學.

利用網絡畫板的技術可以快速得到一個平行四邊形活動框架，并且以動畫的形式展示從不同方向開始變化的平行四邊形形狀.如圖1中的演示界面上呈現的內容，教師可以以交互式教學與學生一起應

用網絡畫板進行操作，點擊“從右向左”或“從左向右”的播放鍵，此時平行四邊形框架中∠α的度數以及兩條對角線的數值都快速呈現在頁面右下方.以動畫的方式展示過程中，學生發現隨著平行四邊形的一個內角的變化成直角時，該活動框架形似矩形，此時的兩條對角線長度相等，由此推出“對角線相等的平行四邊形是矩形”的猜想.整個教學過程更為便捷且直觀，教師與學生在無法獲取實物工具時，網絡畫板不失為一劑良方，特別在智慧課堂——學習平板與希沃白板交互課堂中，學生可以自主進行操作.

3.2 網絡畫板在章節復習課中的應用——“特殊平行四邊形的對角線”

特殊平行四邊形的對角線相關知識是整個章節學習過程中的重點以及難點，菱形、矩形與正方形的兩條對角線的長度或位置關系各不相同，因此可從對角線的長度、角度對特殊平行四邊形的性質與判定進行專項復習.通過網絡畫板可以將菱形、矩形與正方形的對角線特征展示，即平行四邊形的兩條對角線特殊變化引起一般平行四邊形轉化為特殊的平行四邊形，整個動畫演示過程使得學生形成更為深刻的印象，知識結構更為完善.

平行四邊形的兩條對角線互相平分，在此基礎上，利用網絡畫板設置變量進行繪制，以便學生觀察變化進行知識聯結.如圖2中演示界面左側上方顯示兩條對角線長度，平行四邊形的A、C

兩點可以分別進行拖動以改變AC長度.左側下方a表示BDAC的值，拖動滑竿時BD長度會跟隨變化；α角為兩條對角線之間的夾角，已在平行四邊形中標出，拖動滑竿時α角發生變化.點擊“對角線長度變化”播放按鍵，BD長度開始變化，最終形成BD=AC，即平行四邊形兩條對角線相等，從一般平行四邊形變為矩形；點擊“對角線角度變化”播放按鍵，α角開始變化，最終形成α=90°即平行四邊形兩條對角線垂直，從一般平行四邊形變為菱形；同時點擊“對角線長度變化”播放按鍵與“對角線角度變化”播放按鍵，最終形成BD=AC、α=90°即平行四邊形的兩條對角線垂直且相等，從一般平行四邊化為正方形.同時在演示界面的右下方，點擊“線段”與“角度”圖標，可以分別顯示或隱藏平行四邊形四條邊、四個內角的數值.

在教學過程中，通過網絡畫板演示出平行四邊形兩條對角線的變化從而形成不同的特殊平行四邊形，平行四邊形、菱形、矩形以及正方形之間的包含關系也就躍然紙上.

3.3 網絡畫板在習題講解中的應用——“菱形中求線段和最小值”

學生在學習完知識后需要及時鞏固常見的手段就是必要的練習，在《特殊平行四邊形》該章節中幾何圖形的練習中重在考查學生的幾何直觀和推理能力，如利用特殊平行四邊形的性質求解習題.下文對菱形中求線段和最小值一類問題進行應用網絡畫板技術繪制動態演示，以此促進學生的幾何直觀和推理能力的發展.

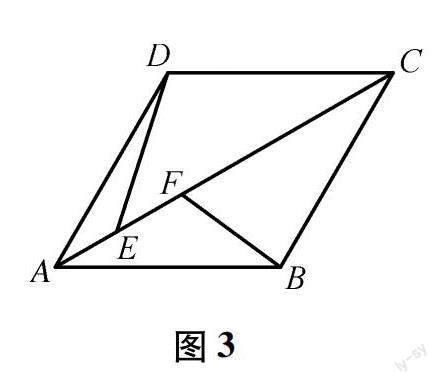
例1 （2020·陜西模擬）如圖3，菱形ABCD的邊長為3，∠BAD＝60°，點E、F在對角線AC上（點E在點F的左側），且EF＝1，則DE+BF最小值為_________.

該題中平行四邊形為特殊平行四邊形——菱形，問題的要求的是DE+BF的最小值，從題中可以發現E點、F點是動點，B點、D點則為定點，但是E點與F點之間存在EF=1，實際上只要考查E點、F點中的一點，則另外一點的位置也隨之而定.于是不妨考慮使得兩個點“合為一個點”，即作出某個線段使得與另一個線段的一端同為一個端點，由于圖中沒有此條件，此時考慮做輔助線.

此題的講解可以利用網絡畫板進行，本文繪制如下圖4所示資源：第一，點擊左側按鈕“幫助”出現E點、F點在AC上移動的軌跡動畫，并且可視DE、BF、DE+BF的值，實際上也可通過拉動E點，發現DE+BF的值會經歷從大到小再到大的過程，引導學生發現存在最小值以及其大致位置；第二，點擊“步驟一”，畫面呈現作輔助線DM∥AC，使得DM=EF=1，則得到四邊形DEFM為平行四邊形，即DE=MF，同時出現“解答過程一”，如何找到將DE、BF化為連接的兩條線段是本題的關鍵，引導學生利用平行四邊形的性質可以作出平行四邊形DEFM，以達到DE=MF；第三，點擊“提示”，F點移動到DM與AC的交點處，即連接BM交AC于F點，當F點為DM與AC的交點，這是依據兩點之間線段最短找到，此時MF+BF的值最小即DE+BF的值最小；第四，點擊“步驟二”，找到符合條件的F點位置后，根據菱形、平行四邊形以及∠BAD＝60°，即連接BD作出直角三角形，利用勾股定理進行求解，同時呈現“解答過程二”.

回望本題，考查了菱形的性質、平行四邊形的判定和性質、兩點之間線段最短、勾股定理等知識，在整個解題中要借助輔助線將問題進行轉化，即兩點之間線段最短.通過網絡畫板進行動態演示的意圖在于，學生在變化中找到特殊的位置，通過觀察后判斷出解題的要點在于畫出輔助線，最終得到結果.

4 結語

信息技術與數學課堂的融合是現代數學教師們在努力嘗試并付諸行動的課題，由于數學的抽象性區別于其他學科，幾何圖形的學習考驗學生的幾何直觀和推理能力，數學教師利用網絡畫板進行相關方面的教學可以起到事半功倍的效果.本文對《特殊平行四邊形》章節中各種課例中可使用網絡畫板環節進行設計繪制并形成網絡分享文件，助力學生發展幾何直觀素養，一線教師以及學生都可以通過掃碼的方式進行觀看以及應用，以期為初中數學教學與信息技術的融合提供一定的參考.

參考文獻：

［1］ 中華人民共和國教育部. 義務教育數學課程標準（2022年版）［S］. 北京：北京師范大學出版社，2022.

［2］ 張景中，葛強，彭翕成. 教育技術研究要深入學科［J］. 電化教育研究，2010（2）：8-13.

［3］ 王鵬遠. 網絡畫板平臺支持下的新一代數學實驗室［J］. 中小學信息技術教育，2018（6）：54-56.

［4］ 方海光，魏文雅，劉嘉琪，張景中. 互聯網數學實驗室支持的智慧課堂實驗活動研究［J］.中小學數字化教學，2019（6）：24-27.

［5］ 單墫.解題研究［M］.上海：上海教育出版社，2013.

［6］ 劉敏.巧作輔助線解決梯形相關的幾何問題［J］.數理天地（初中版），2022（7）：67-69.