熱力聯合作用下熱塑性復合材料懸臂梁的彈塑性分析
唐雨 雷勇軍 吳棟 于寶石 張大鵬


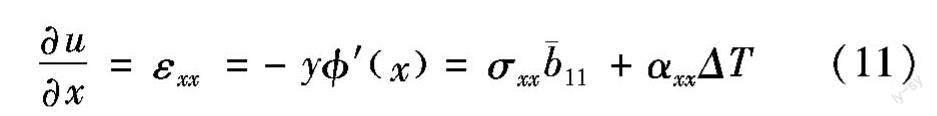
基金項目:國防科技大學自主創新科學基金項目“可重復使用碳纖維增強熱塑性復合材料力學特性與失效機理研究”(22-ZZCX-077)。
通訊作者:張大鵬,男,副教授。研究方向為計算固體力學理論與應用方向。E-mail: zhangdapeng@nudt.edu.cn
摘 要 纖維增強熱塑性復合材料由于基體韌性的增大導致其彈塑性特性突出,而考慮溫度影響后其力學行為則更為復雜。考慮非線性熱載荷與彎矩聯合作用的影響,基于Timoshenko梁和塑性線性強化理論,建立了針對纖維增強熱塑性復合材料懸臂直梁彈塑性問題的理論分析模型,得到了懸臂直梁應力和位移的解析解,并將解析解分別與文獻和有限元的計算結果進行對比,驗證了所建理論分析模型的正確性。在此基礎上,分析了不同彎矩、纖維鋪層角和跨高比對懸臂直梁彈塑性行為的影響。相關結論可為纖維增強熱塑性復合材料的設計和工程應用提供參考。
關鍵詞 熱塑性復合材料;熱力聯合;彈塑性;懸臂直梁;本構模型
Elastic-plastic Analysis of Thermoplastic Composite?Cantilever Beams Under Combined?Thermodynamic Action
TANG Yu1,2, LEI Yongjun1,2,WU Dong1,2, YU Baoshi1,2,ZHANG Dapeng1,2
(1.College of Aerospace Science and Engineering, National University of?Defence Technology,Changsha 410073;2.Hunan Key Laboratory of Intelligent Planning?and Simulation for Aerospace Missions,Changsha 410073)
ABSTRACT The elastoplastic properties of fiber-reinforced thermoplastic composites are prominent due to the increase of matrix toughness, but the mechanical behaviors of fiber-reinforced thermoplastic composites are more complicated considering the influence of temperature. Considering the combined effects of nonlinear thermal loads and bending moments, a theoretical analysis model for the elastoplastic problem of a cantilever straight beam reinforced with fiber reinforced thermoplastic composites is established based on Timoshenko beam and the theory of plastic linear strengthening. The analytical solutions of the stress and displacement of the cantilever straight beam are obtained, and the analytical solutions are compared with the calculated results in literature and finite element respectively. The correctness of the theoretical analysis model is verified. On this basis, the effects of different bending moments, fiber ply Angle and span height ratio on the elastic-plastic behavior of the cantilever beam are analyzed. These conclusions can provide reference for the design and engineering application of fiber reinforced thermoplastic composites.
KEYWORDS thermoplastic composites; thermal union; elasticity; cantilever straight beam; principal structure model
1 引言
在航空航天領域,飛行器既要滿足結構功能特性,同時還要充分的考慮減重優化,從而具備更好的結構設計靈活性,所以,其對材料的綜合性能需求日益增加[1]。復合材料由于引入增強纖維并通過基體的協同賦予了其相較于傳統金屬材料更加優越的比剛度、比強度,且有效降低了飛行器結構的重量,提高了有效載荷。與熱固性復合材料相比,以聚醚醚酮(PEEK)、聚苯硫醚(PPS)等基體為代表的高性能纖維增強熱塑性復合材料具有韌性高、損傷容限大、抗沖擊性能、耐熱性好等優點,同時兼具可在線修復和可重復使用的特性,被認為是未來航空航天結構邁向輕量化、功能化與綠色環保化的有效途徑之一。目前,纖維增強熱塑性復合材料已初步應用于航空領域中的電子氣動外殼、電子復雜構件等結構件以及航天領域中的整流罩、適配器、網狀發射器等結構件,并在升級換代過程中不斷提高應用比例,成為制造現有和未來飛行器不可或缺的關鍵材料[2-3]。
實驗表明[4-5],溫度對纖維增強熱塑性復合材料的力學行為有顯著的影響,開展溫度對其力學性能的影響研究是有必要的。Wang等[6]從不同層面討論了纖維增強熱塑性復合材料的殘余熱應力的形成原因,并進一步研究了基于非破壞性和破壞性方法的殘余熱應力測試方法。Eacute等[7]建立了一個熱力學模型來預測復合材料薄板在冷卻成型過程中的應變和應力狀態,并解釋了層壓板的傳熱、結晶動力學和力學行為。Tullu等[8]開發了基于徑向基函數(RBF)的數學模型,模擬了熱塑性復合材料成型過程中的層間剪切應力。
纖維增強熱塑性復合材料是典型的正交各向異性材料,且由于基體韌性增加而具有明顯的彈塑性力學特性[9],使用過程中材料一旦發生塑性變形,可能會導致結構過早失效。在對纖維增強熱塑性復合材料的彈塑性分析中,國內外學者們目前主要采用的方法包括有限元法、解析法和半解析法。在均勻熱載荷下,Sen等[10]采用有限元法對粘合的單層搭接纖維增強熱塑性復合材料進行了彈塑性分析,并指出材料的正交各向異性特性導致其不同方向熱應力差異較大。Ucsular等[11]采用有限元法分析了熱塑性復合材料帶孔圓盤冷卻時的塑性力學性能,結果表明,孔的尺寸對圓盤冷卻時的塑性變形區域有重要影響。Sen等采用有限元法分別對溫度沿著熱塑性復合圓盤的徑向截面從內表面到外表面呈線性變化[12]和拋物線變化[13]兩種情況下的彈塑性力學行為進行了分析。Ondurucu等采用半解析法對溫度沿著熱塑性復合材料層壓板的厚度呈拋物線變化[14]的彈塑性力學行為進行了分析。Arslan等[15]基于理想彈塑性理論,對自由端受集中力加載的懸臂梁進行分析,得到了彈性段和塑性段材料的應力解,但該研究中采用的理想彈塑性模型不能較好地描述材料的實際彈塑性力學行為。Wang等[16]采用線性強化彈塑性理論對偏軸張力下的懸臂梁進行了彈塑性分析。對于纖維增強熱塑性復合材料短粗梁,雷勇軍等[17]通過Timoshenko梁理論獲得了自由端受彎矩懸臂梁的應力位移解,結果表明,使用Timoshenko梁理論可在一定程度上提高求解精度。
考慮溫度影響下對熱塑性復合材料彈塑性力學性能的研究中,較多使用有限元法和半解析法。然而,基于連續介質力學理論推導的彈塑性分析的解析表達式,可以從機理層面對彈塑性行為做出解釋。
因此,本文基于Timoshenko梁和塑性線性強化理論,建立非線性熱載荷和彎矩作用下的懸臂直梁彈塑性理論分析模型,采用解析解方法得到懸臂直梁的應力與位移解,通過與文獻和有限元的計算結果進行對比來驗證理論分析模型的正確性。最后分析不同彎矩、纖維鋪層角和跨高比對熱塑性復合材料彈塑性響應的影響規律。
2 熱力聯合作用下彈塑性分析模型
建立纖維增強熱塑性復合材料懸臂梁幾何模型,如圖1所示,懸臂梁長為l,高為2c,厚為t,材料坐標系為1o2,o1為纖維鋪層方向,全局坐標為xoy,全局坐標與材料坐標夾角為θ。梁左端固支,右端受彎矩作用,高度方向受一個非線性變化的熱載荷ΔT。
2.1 彈性段建模
假設纖維增強熱塑性復合材料是正交各向異性的,且在xoy平面內滿足平面問題假設,考慮溫度的影響,則其本構方程如公式(1)所示。
其中,b-ij、bij(i或j=1、2、6)分別為全局坐標系xoy下和材料坐標系1o2下柔度矩陣中各項元素,ΔT表示溫度變化,αxx、αyy表示在x軸、y軸方向的熱膨脹系數,β為xoy坐標系與1o2坐標系的轉換矩陣。
熱膨脹系數在全局坐標系xoy方向上的分量如公式(2)所示。
其中,α1、α2表示在材料坐標系1o2方向的熱膨脹系數。
對于平面應力問題的幾何方程,如公式(3)所示。
設應力函數為φx,y,σxx、σyy和σxy可表達如公式(4)所示。
考慮熱載荷后,懸臂梁自由端僅受彎矩,即∫-c+cσxxytdy=M,可知σxx僅與y相關,可假設應力函數的表達式如公式(5)所示。
φx,y=yAx+Bx+Cy ???(5)
其中,Ax和Bx為僅含x的待求函數、Cy為僅含y的待求函數。將公式(5)代入公式(4),得到的結果如公式(6)所示。
結合公式(1)、公式(3)和公式(6),可得控制方程,如公式(7)所示。
熱膨脹在沒有約束下不產生力,對自由端受彎矩的懸臂梁模型,邊界條件如公式(8)所示。
懸臂梁在高度方向上受非線性熱載荷,設熱載荷為ΔT=gy2,其中g為熱載荷梯度。聯立公式(6)、公式(7)和公式(8)解得彈性階段應力解,如公式(9)所示。
根據Timoshenko梁理論,得出如公式(10)所示。
其中?x為轉角。
聯立公式(1)、公式(3)和公式(10)可得,如公式(11)所示。
結合邊界條件?l,y=0,對公式(11)積分可得如公式(12)所示。
其中,y≠0,考慮位移連續,計算軸向位移時,忽略y=0的奇點。將公式(12)代入公式(10),根據邊界條件ul,y=0,可得懸臂梁彈性階段軸向位移u表達式如公式(13)所示。
由公式(1)、公式(3)和公式(13),再根據邊界條件vl,0=0,可得懸臂梁彈性階段橫向位移v表達式如公式(14)所示。
2.2 彈塑性段理論建模
采用Tsai-Hill屈服準則可以有效描述熱塑性復合材料屈服狀態[18]。假設熱塑性復合材料為線性應變強化、拉壓同性材料。對于拉壓同性材料,Tsai-Hill屈服準則可如公式(15)所示。
其中,X、σ11為熱塑性復合材料沿纖維方向的屈服強度與應力,Y、σ22為垂直纖維方向的屈服強度與應力,S12、σ12為面內剪切強度與應力。
根據公式(15)定義等效應力,如公式(16)所示。
在材料主軸方向的應力分量,如公式(17)所示。
將公式(17)代入公式(16),得出等效應力如公式(18)所示。
進入屈服階段后,基于線性強化假設,屈服應力可由Ludwik方程表示,如公式(19)所示。
其中,σ0的大小為X,K為塑性常數,εpeq為等效塑性應變。熱塑性復合材料屈服條件滿足如下關系,如公式(20)所示。
其中,X1為σxx達到屈服條件下的應力值,即當σxx值大于X1時,熱塑性復合材料進入塑性階段。
對于塑性階段,選用相關塑性流動法則,得到材料坐標系1o2下的塑性應變增量,如公式(21)所示。
發生塑性變形后,應變增量等于彈性階段應變增量加上塑性應變增量,即dε=dεe+dεp,對公式(21)積分,可得熱塑性復合材料在材料坐標系1o2下的總應變增量如公式(22)所示。
其中,C1、C2和C3為積分后對應的常數,對于全局坐標系xoy坐標系下,懸臂梁塑性區域的應變分量如公式(23)所示。
根據全局坐標系xoy坐標系與纖維坐標1o2轉換矩陣β,結合公式(22),可得常數項C4、C5、C6如公式(24)所示。
結合彈性階段應力解公式(9),懸臂梁應力解如公式(25)所示。
其中,懸臂梁的上下表面首先進入塑性,-c,-h1與h2,c分別為懸臂梁上表面和下表面處發生塑性的區域,h1,h2為彈性區域,m、n為待求常數。
根據Bernoulli-Navier假設[19]得出如公式(26)所示。
其中,ρ為曲率半徑,由于梁在彈塑性分界區域有σxx=X1,再聯立公式(1)、公式(23)和公式(26)可得如公式(27)所示。
在彈塑性邊界處有σxx=X1,代入公式(25),可得如公式(28)所示。
根據公式(1),再結合公式(10),以及邊界條件?l,y=0,以0 將公式(1)、公式(3)、公式(25)和式(29),代入邊界條件,得出如公式(30)所示。 求得懸臂梁橫向位移v的表達式如公式(31)所示。 3 結果分析 3.1 模型驗證 文獻[17]基于Timoshenko梁和塑性線性強化理論,建立了彎矩作用下纖維增強熱塑性復合材料懸臂梁模型,得到了應力與位移的彈塑性解析解。文獻[20]基于Timoshenko梁理論分析了彎矩作用下雙層復合材料懸臂直梁的彈性靜變形。但文獻[17]和[20]都未考慮溫度對熱塑性復合材料彈塑性力學性能的影響,為驗證本文所建理論分析模型的正確性,在忽略熱載荷情況下,通過設置與文獻[17]一致的材料及幾何參數來進行對比研究,參考點設在懸臂梁自由端的下表面處。本文應力、位移計算結果與文獻和有限元對比結果如表1所示。由表1可知,本文所建理論分析模型在純彈性與彈塑性分析下得到的位移解和應力解均與文獻和有限元結果吻合較好。 為進一步驗證本文模型的正確性,考慮非線性熱載荷作用下,將本文理論分析模型與有限元的計算結果進行對比。材料基本參數[21]如表2所示,幾何參數設懸臂梁長l為80mm、高2c為12mm、厚t為6.4mm,彎矩M=2000N·mm,纖維的鋪層角θ=45°。有限元分析采用雙線性平面應力四邊形單元,劃分3840個單元,屈服準則為各向異性Tsai-Hill屈服準則,硬化方式為各向同性硬化,所建有限元模型材料參數及幾何參數與本文理論分析模型一致。 本文理論分析模型與有限元計算結果在高度方向上的應力(σxx)截面分布變化曲線如圖(2)所示,其中圖2(a)是未考慮塑性變形時應力截面分布,圖2(b)是考慮塑性變形時應力截面分布。從圖2中可以看出,在不同熱載荷下本文理論分析模型與有限元計算結果吻合較好。以上分析驗證了本文所建理論分析模型的正確性。 通過圖2(a)可知,當懸臂梁未發生塑性變形時,在不同的熱載荷作用下其應力截面分布差異明顯,主要表現在熱載荷ΔT=gy2中的梯度g越大,懸臂梁上表面應力絕對值越大,而下表面處應力隨之越小。 圖2(b)可以看出,當發生塑性變形后,熱載荷越大,懸臂梁上表面處塑性區域也越大,而懸臂梁下表面處塑性區域則有減小趨勢。造成該現象的原因是在懸臂梁上表面處,熱應力與彎矩作用下的應力方向是相同的,而在下表面處方向相反。該規律也可以通過公式(9)進行解釋,由于應力表達式為二次函數,熱載荷越大導致其二次項系數f/2越大,進而導致此現象。在驗證本文理論模型正確性的基礎上,下面進一步分析不同彎矩、纖維鋪層角和跨高比對彈塑性響應的影響規律。 3.2 影響因素分析 3.2.1 彎矩對懸臂梁應力和位移的影響 在本節及后續的計算中,如無特別說明,基本材料及幾參數同上述表2,溫度變化取ΔT=y2,計算位移橫截面取x=20mm。圖3給出了不同彎矩下純彈性分析與彈塑性分析的應力、位移截面分布情況。 不考慮熱載荷(ΔT=0)時,由公式(9)可以看出,此時應力截面分布是一個過點(y=0,σxx=0)的一次函數;僅考慮熱載荷作用下(M=0kN·mm)時,由公式(9)和圖3(a)中均可以看出此時應力截面分布是一個對稱軸為y=0的二次函數;同時考慮熱載荷和彎矩的作用,應力截面分布可看成是二次函數與一次函數疊加作用的結果。 對比圖3(a)與圖3(b)中彈性區域的應力截面分布,圖3(b)相比與圖3(a)應力增長更快,且隨著彎矩增大,懸臂梁上表面率先發生塑性變形,上表面塑性變形區域隨彎矩的增大而增大。這是由于發生塑性變形后,懸臂梁上下表面處率先發生塑性變形,而塑性區域承受應力增長緩慢,導致懸臂梁中部的彈性區域應力增量更大。從推導的理論模型也可以看出,發生塑性變形后,為保證力邊界條件公式(8)的連續性,導致應力數值在懸臂梁彈性區域增長明顯。 在圖3(c)軸向位移u分布中,發生塑性變形后曲線斜率的絕對值將變大。而力越大,變形和產生的位移越大,在發生塑性變形后,彈性區域應力斜率增大,所以軸向位移u斜率絕對值變大;在懸臂梁塑性區域,應變由彈性應變和塑性應變組成,而公式(23)中計算結果表明C4比11大4個數量級,即發生塑性變形后,塑性應變增量是大于彈性應變增量,因此圖3(c)中軸向位移u在塑性區域的斜率絕對值要比彈性區域更大。 從圖3(d)中可知,隨著彎矩的增加,橫向位移v絕對值增大,橫向位移v絕對值在彈塑性分析要比純彈性分析下增大更加顯著,可以根據位移解析式做出合理解釋。 3.2.2 纖維鋪層角對懸臂梁應力和位移的影響 本節分析不同纖維鋪層角θ對懸臂梁應力與位移的影響,其中M取1000N·mm。纖維鋪層角θ對懸臂梁應力和位移截面分布影響情況如圖4所示。 從圖4(a)可以看出在純彈性分析中隨θ減小,懸臂梁上表面的應力絕對值減小,而下表面的應力值增大。由表達式(9)可以得出,當懸臂梁不受熱載荷作用時,θ的變化不會對懸臂梁應力數值產生變化,只對有熱載荷作用時產生影響。具體影響的大小表現在:在懸臂梁上表面時,θ=50°相比θ=90°應力絕對值小了11.20%,在懸臂梁下表面時,應力絕對值大了48.98%。而當熱載荷分別取ΔT=y2/3與ΔT=3y2時,在懸臂梁上表面時,應力絕對值分別小了5.03%、18.97%;在懸臂梁下表面時,應力分別大了7.69%、61.91%。說明熱載荷越大,這種影響越明顯。 由圖4(b)可知纖維鋪層角θ越大,懸臂梁越容易達到屈服條件,上表面處發生塑性變形區域越大。因為熱塑性復合材料的抗彎強度主要是由纖維提供,且沿著纖維方向的強度遠大于垂直纖維方向,因此纖維鋪層角θ越大,抗彎強度越小。根據式(20),σxx達到屈服條件下時應力值X1只和纖維鋪層角θ以及材料固有參數相關,不同的纖維鋪層角θ導致X1的數值變化從而對懸臂梁應力與位移產生影響。所以當鋪層角較小時,將更難達到屈服條件。 由圖4(b)可知,隨θ增大,在懸臂梁上表面越容易發生屈服,應力絕對值將相應減小,而為保證邊界條件公式(8)成立,懸臂梁下表面應力也將增加,此時上下表面應力發生明顯變化,在懸臂梁上表面,θ=50°相比θ=90°應力絕對值大了62.03%,在下表面應力小了11.88%。 由圖4(c)可知,θ越大,軸向位移u截面分布曲線斜率的絕對值越大,彈塑性分析斜率比純彈性分析絕對值大,3.2.1節分析指出軸向位移u分布與應力截面分布和應變成正比,在發生塑性變形后,總應變將明顯增加。由于θ越大,塑性變形區域越大,再結合應力截面分布規律,可以得出此規律原因。由圖4(d)可知,θ越大,塑性區域越多,進一步橫向位移v絕對值越大,對此規律解釋同軸向位移u截面分布分析。 3.2.3 跨高比對懸臂梁彈塑性應力的影響 本節計算取θ=50°,M=1000N·mm,通過改變懸臂梁的高(2c)的大小從而改變跨高比(l/2c),跨高比越大,則表示懸臂梁高(2c)越小。 3.2.1節指出,懸臂梁的應力截面分布是熱載荷與彎矩共同作用的結果。從公式(9)可以看出,跨高比越大(2c變小),應力解中代表彎矩作用的一次函數斜率越大,而對應熱載荷作用的二次函數整體下移。因此圖5(a)中,l/2c=80/8時,懸臂梁應力截面分布主要表現為代表彎矩作用的一次函數的影響;l/2c=80/12時,懸臂梁應力截面分布表現的是彎矩和熱載荷疊加作用的影響;l/2c=80/20時,懸臂梁應力截面分布主要表現熱載荷作用的影響。即跨高比越大,彎矩對懸臂梁的應力截面分布影響越大;跨高比越小,熱載荷對懸臂梁的應力截面分布影響越大。 由圖5(b)可知,在考慮塑性變形后,懸臂梁上表面先達到塑性,當l/2c=80/8時,懸臂梁的截面87.91%都是達到塑性狀態,結構從懸臂梁上下表面往懸臂梁中部處快速失效;當l/2c=80/12、80/20時,懸臂梁的塑性區域分別占3.88%和4.48%。可以得出,在懸臂梁的彈塑性分析中,跨高比較小時,懸臂梁上表面處率先發生屈服,懸臂梁中部應力增長明顯,而隨跨高比增大,懸臂梁更容易發生屈服。 4 結語 (1)建立的熱力聯合作用下熱塑性復合材料彈塑性理論模型物理意義明確,可有效得出彈塑性狀態下應力位移解; (2)熱載荷作用的效果受纖維鋪層角的影響明顯,纖維鋪層角度越大,越容易導致發生屈服,合理設置纖維鋪層角可改變塑性變形的區域; (3)熱載荷顯著影響懸臂梁的塑性區域,且跨高比越大,懸臂梁應力截面分布受熱載荷的影響越小,但懸臂梁發生塑性變形區域越大。 參 考 文 獻 [1]陳超,張帥,倪敏軒,等.自動鋪層技術在民航復合材料的應用及發展[J].纖維復合材料,2022,39(4):131-134. [2]趙天,李營,張超,等.高性能航空復合材料結構的關鍵力學問題研究進展[J].航空學報,2022 ,43(6) :526851. [3]VAIDYA U, 李進松, 管佳明. 熱塑性復合材料在航空航天中的應用[J]. 航空制造技術, 2015, (14): 69-71. [4]ZHANG Y, SUN L, LI L, et al. Effects of strain rate and high temperature environment on the mechanical performance of carbon fiber reinforced thermoplastic composites fabricated by hot press molding[J]. Composites: Part A, Applied Science & Manufacturing, 2020, 134: 105905. [5]WANG S, WEN L, XIAO J, et al. The Out-of-Plane Compression Response of Woven Thermoplastic Composites: Effects of Strain Rates and Temperature[J]. Polymers, 2021, 13(2): 264. [6]WANG C, YUE G, ZHANG J, et al. Formation and test methods of the thermo-residual stresses for thermoplastic polymer matrix composites[C]. 2016年土木、建筑與環境工程國際學術會議, 2016: 607-610. [7]EACUTE, RON M, JACQUEMIN F, et al. Measurement and prediction of residual strains and stresses during the cooling of a glass fibre reinforced PA66 matrix composite[J]. Composites: Part A, Applied Science & Manufacturing, 2020, 137: 106039. [8]TULLU A, LEE B-S, Hwang H-Y. Surrogate Model Based Analysis of Inter-Ply Shear Stress in Fiber Reinforced Thermoplastic Composite Sheet Press Forming[J]. Appl. Sci., 2020, 10(16). [9]CHILALI A, ZOUARI W, ASSARAR M, et al. Analysis of the mechanical behaviour of flax and glass fabrics-reinforced thermoplastic and thermoset resins[J]. Journal of Reinforced Plastics and Composites, 2016, 35(16): 1217-1232. [10]SEN F. Elastic-plastic thermal and residual stress analysis of adhesively bonded single lap joint[J]. Advanced Composites Letters, 2016, 25(1): 22-28. [11]UCSULAR I A, ZOR M B, SAYMAN O B. Hole diameter effects on fiber-reinforced thermoplastic composite discs possessing distinct fiber arrays under thermal loading(Article)[J]. Journal of Thermoplastic Composite Materials, 2014, 27(10): 1334-1348. [12]SEN F, ALDAS K. Elastic-plastic thermal stress analysis in a thermoplastic composite disc applied linear temperature loads via FEM[J]. Advances in Engineering Software, 2009, 40(9): 813-819. [13]SEN F. The Effect on Thermal and Residual Stresses of Parabolic Temperature Loading in a Thermoplastic Composite Disc[J]. Journal of Reinforced Plastics and Composites, 2008, 27(1): 51-67. [14]ONDURUCU A, TOPCU M. Thermal Residual Stresses in Simply Supported Thermoplastic Laminated Plates under a Parabolic Temperature Distribution[J]. Journal of Thermoplastic Composite Materials, 2006, 19(2): 155-171. [15]ARSLAN N, ZBEN T. An Elastic-Plastic Stress Analysis in a Unidirectional Reinforced Steel Fiber Thermoplastic Composite Cantilever Beam Loaded by a Single Force at the Free End[J]. Journal of Reinforced Plastics and Composites, 2005, 24(5): 457-469. [16]WANG X, DONG K, XIAO J. An analytical method for elastic-plastic stress in a thermoplastic composite cantilever beam subjected to bias-axis tension load[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2005, 219(10): 1017-1026. [17]雷勇軍, 劉明偉, 張大鵬, 等. 彎矩作用下熱塑性復合材料懸臂梁彈塑性分析[J]. 國防科技大學學報, 2022, 44(2): 24-33. [18]張貴杰, 夏亮亮, 楊莉英, 等. 屈服準則研究的新進展[J]. 鑄造技術, 2017, 38(01): 20-23. [19]SAYMAN O, AKSOY S, AYKUL H. An elastic/plastic solution for a thermoplastic composite cantilever beam loading by bending moment[J]. Composites Science and Technology, 2000, 60(14): 2739-2745. [20]BALDUZZI G,MORGANTI S,FüSSL J, et al. Modeling the non-trivial behavior of anisotropic beams: a simple Timoshenko beam with enhanced stress recovery and constitutive relations [J]. Composite Structures, 2019, 229:111265. [21]BEKTAS N B, SAYMAN O. Elastic-plastic stress analysis on simply supported thermoplastic laminated plates under thermal loads varying linearly[J]. Journal of Reinforced Plastics and Composites, 2003, 22(2): 149-168.

