采用改進多尺度符號動力學(xué)熵的鐵路機車軸承故障診斷

張龍 劉皓陽 肖乾

摘要：針對鐵路機車軸承在真實復(fù)雜環(huán)境下故障特征難以提取而導(dǎo)致故障診斷困難的問題，提出一種改進多尺度符號動力學(xué)熵（IMSDE）的鐵路機車軸承故障診斷方法。首先，通過鄰域滑移均值化的方式改進多尺度符號動力學(xué)熵，克服了傳統(tǒng)粗粒化造成的熵值偏差缺陷；然后，利用IMSDE充分提取振動信號在不同尺度下的關(guān)鍵故障特征；最后，結(jié)合極限學(xué)習(xí)機（ELM）實現(xiàn)鐵路軸承不同故障類型與程度的識別。在此基礎(chǔ)上，分別進行了3組試驗分析。結(jié)果表明，對人為構(gòu)造的軸承故障和工程實際產(chǎn)生的軸承故障，該方法都具有精準的故障識別效果，對比其他4種方法故障識別率更高，驗證了該方法具有一定的工程實際應(yīng)用價值。

關(guān)鍵詞：機車軸承；故障診斷；特征提取；多尺度符號動力學(xué)熵；極限學(xué)習(xí)機

中圖分類號：U279；TH133.33 文獻標志碼：A

本文引用格式：張龍，劉皓陽，肖乾. 采用改進多尺度符號動力學(xué)熵的鐵路機車軸承故障診斷[J]. 華東交通大學(xué)學(xué)報，2023，40（5）：32-40.

Fault Diagnosis of Railway Locomotive Bearings Using Improved Multiscale Symbolic Dynamic Entropy

Zhang Long1，2，Liu Haoyang1，2，Xiao Qian1，2

（1. Key Laboratory of Conveyance and Equipment of Ministry of Education， East China Jiaotong University， Nanchang 330013， China； 2. State Key Laboratory of Performance Monitoring and Protecting of Rail Transit Infrastructure， East China Jiaotong University， Nanchang 330013， China）

Abstract：Aiming at the problem that it is difficult to extract the fault features of railway locomotive bearings in a real complex environment， which leads to the difficulty of fault diagnosis， an improved multiscale symbolic dynamic entropy（IMSDE） fault diagnosis method is proposed. Firstly， the MSDE is improved by utilizing neighborhood slip averaging， which overcomes the defects of entropy deviation caused by traditional coarse-graining. Then， IMSDE is used to fully extract the key fault features of vibration signals at different scales. Finally， the identification of different fault types and degrees of railway bearings is achieved by combining with an extreme learning machine（ELM）. On this basis， three separate sets of tests were analyzed. The results show that the method has an accurate fault identification effect for both artificially constructed bearing faults and bearing faults generated by engineering reality， and the fault identification rate is higher compared with the other four methods， which verifies that the method has a certain value of practical application in engineering.

Key words： locomotive bearing; fault diagnosis; feature extraction; multiscale symbolic dynamic entropy; extreme learning machine

Citation format：ZHANG L，LIU H Y，XIAO Q. Fault diagnosis of railway locomotive bearings using improved multiscale symbolic dynamic entropy[J]. Journal of East China Jiaotong University，2023，40（5）：32-40.

滾動軸承可以同時承受徑向與軸向聯(lián)合負載作用，是維持鐵路機車正常運轉(zhuǎn)的重要零部件。由于長期處于復(fù)雜的環(huán)境下，發(fā)生疲勞點蝕和塑性變形的概率極高，最終會導(dǎo)致軸承完全失效[1-3]。因此，能夠及時、有效的對鐵路機車軸承進行故障診斷就顯得尤為重要。但是，由于受到噪聲、信號衰減以及復(fù)雜傳輸路徑等因素的影響，使軸承振動信號所含有效故障信息較為輕微，特征難以被提取，進而影響故障診斷模型的建立[4]。

熵作為度量時間序列復(fù)雜性的一種工具，已經(jīng)被廣泛應(yīng)用于旋轉(zhuǎn)機械的健康監(jiān)測。一些學(xué)者通過提取旋轉(zhuǎn)機械不同健康狀態(tài)下的熵值特征，然后對其進行故障診斷[5-6]。傳統(tǒng)的熵值計算方法有兩種，分別是樣本熵（sample entropy，SE）和排列熵（permutation entropy，PE）。但是，上述方法分別存在計算時間長、受噪聲干擾嚴重等問題。王斐等[7]提出了一種多尺度樣本熵（multiscale sample entropy，MSE）的方法，結(jié)果證明可以識別軸承不同類型的故障。鄭近德等[8]通過多尺度排列熵（multiscale permutation entropy，MPE）提取特征并結(jié)合支持向量機（support vector machine，SVM）實現(xiàn)滾動軸承的故障診斷。然而，對于較長的時間序列，MSE仍存在計算速度慢的缺點。雖然MPE計算速度有所提升，但是僅考慮信號幅值在升序排列時不同數(shù)值的大小關(guān)系，容易導(dǎo)致故障信息丟失[9-10]。

為了應(yīng)對上述問題，李永波提出了一種衡量復(fù)雜度計算的新方法—符號動力學(xué)熵（symbolic dynamic entropy，SDE），并在SDE的基礎(chǔ)上結(jié)合多尺度分析，提出了多尺度符號動力學(xué)熵（multiscale symbolic dynamic entropy，MSDE）[11]。相比于MSE和MPE，MSDE克服了故障信息在單一尺度下難以被充分提取的缺陷，在多尺度下將時間序列的幅值大小進行符號化，能夠捕捉到振動信號實際的幅值信息，因此擁有更高的計算效率和更強的魯棒性。Han等[12]提出了一種局部均值分解（local mean decomposition， LMD）和MSDE相結(jié)合的滾動軸承故障診斷方法，并且驗證了該方法有效性。然而，隨著尺度的不斷增大，傳統(tǒng)粗粒化方式將會引起時間序列急劇縮小，進而導(dǎo)致關(guān)鍵故障信息難以被充分挖掘。

綜上，針對鐵路機車軸承在復(fù)雜環(huán)境下難以提取故障特征而導(dǎo)致故障診斷困難的問題，本文提出一種改進多尺度符號動力學(xué)熵（improved multiscale symbolic dynamic entropy，IMSDE）的鐵路機車軸承故障診斷方法。首先，采用鄰域滑移均值化的方式改進傳統(tǒng)的粗粒化過程；然后，利用IMSDE充分地提取非線性振動信號的關(guān)鍵故障特征并構(gòu)建特征矩陣；最后，將特征矩陣隨機劃分的訓(xùn)練集輸入ELM中形成故障診斷模型，并通過測試集進行驗證，最終實現(xiàn)鐵路軸承不同故障類型與程度的識別，為提高鐵路工程故障診斷模型精度提供了一種有效的方法。

1 改進的多尺度符號動力學(xué)熵

1.1 多尺度符號動力學(xué)熵

采用SDE計算時間序列X=[x1，x2，…，xN]的過程可以劃分為4個步驟。

1.2 改進多尺度符號動力學(xué)熵

通過上述粗粒化分析可知，尺度因子τ的大小與時間序列的長短成反比。因此，當(dāng)τ取值越大時，時間序列越短，可能造成熵值計算出現(xiàn)誤差。為了解決這一問題，采用鄰域滑移均值化代替?zhèn)鹘y(tǒng)粗粒化的方法，其方法主要分為兩個過程。

1） 鄰域滑移均值化：通過鄰域滑動平均的方式對時間序列Uj=[u1，u2，…，uN]進行處理，第k個滑移均值化序列為

式中：1≤k≤τ。

2） 計算所有尺度IMSDE

IMSDE鄰域滑移均值化是對粗粒化過程進一步的細化，相比于MSDE粗粒化方式，IMSDE考慮了同一類別相鄰點之間的符號動力學(xué)特性，不會將狀態(tài)模式相異的嵌入矢量視為同一種符號動力學(xué)模式，因此可以有效解決熵值誤差這一問題。

1.3 參數(shù)討論分析

由上述分析可知，IMSDE需要預(yù)先設(shè)置4個參數(shù)。分別為：尺度因子τ，符號數(shù)ε，時間延遲λ以及嵌入維度m，不同參數(shù)設(shè)置可能導(dǎo)致特征提取效果具有明顯的差異。采用仿真白噪聲對上述參數(shù)進行分析，然后通過MSDE進行對比。

1） 符號數(shù)ε：通過控制嵌入維度m，尺度因子τ以及時間延遲λ的大小來確定符號數(shù)ε的影響。圖1為m=3，τ=[1，20]，λ=1時IMSDE和MSDE的熵值變化曲線。由圖1（a）可以看出，隨著ε的增大，MSDE呈現(xiàn)遞減的趨勢，并且不同ε熵值差異明顯。由圖1（b）可以看出，隨著ε的增大，IMSDE遞減的趨勢減弱，在τ=20時熵值保持穩(wěn)定。通過對比分析可知，相比于MSDE，IMSDE熵值變化更小，具有更好的魯棒性。當(dāng)ε<7時，IMSDE包含的狀態(tài)模式減少，不同尺度下熵值接近，無法充分捕捉數(shù)據(jù)中動力學(xué)特性；當(dāng)ε≥9時，IMSDE無法消除背景噪聲的干擾，可能造成熵值計算出現(xiàn)偏差。綜上所述，當(dāng)且僅當(dāng)ε=8時，IMSDE才能有效實現(xiàn)信號在不同尺度下的動力學(xué)特性提取。

2） 嵌入維度m：通過控制符號數(shù)ε，尺度因子τ以及時間延遲λ的大小來確定嵌入維度m的影響。圖2為ε=8，τ=[1，20]，λ=1時IMSDE和MSDE的熵值變化曲線。通過圖2（a）和圖2（b）對比可知，經(jīng)過鄰域滑移均值化處理的IMSDE波動較小，具有更高的穩(wěn)定性。當(dāng)m<3時，構(gòu)成向量的狀態(tài)模式較少，將呈現(xiàn)狀集中分布，法充分檢測時間序列是否發(fā)生突變，不同尺度下熵值難以區(qū)分；當(dāng)m≥3時， IMSDE逐漸趨于平穩(wěn)，但隨著狀態(tài)模式增多，時間成本將會升高，總體運行效率將會下降。當(dāng)m=3時，IMSDE才能在較短的時間內(nèi)實現(xiàn)時間序列動力學(xué)特性的精準表達。綜上所述，本文選擇嵌入維度為m=3。

3） 時間延遲λ：通過控制符號數(shù)ε，嵌入維度m以及尺度因子τ的大小來確定時間延遲的影響。圖3為ε=8，τ=[1，20]，m=3時IMSDE和MSDE的熵值變化曲線。可以清楚看出，不同λ下IMSDE基本重合，MSDE小部分差異，證明了IMSDE具有更優(yōu)的一致性，也說明了λ對熵值計算影響較小。綜上所述，本文選擇時間延遲為λ=1。

2 極限學(xué)習(xí)機

ELM（extreme learning machiane）是一種單隱層前饋神經(jīng)網(wǎng)絡(luò)算法，其模型如圖4所示。由圖4可看出該模型的網(wǎng)絡(luò)結(jié)構(gòu)主要由輸入層、隱含層以及輸出層構(gòu)成。其核心思想是通過設(shè)定隱含層節(jié)點數(shù)，在求解出輸出權(quán)重后使其最小化，從而達到模型泛化性能最大化。由于輸入權(quán)重和隱含層閾值無需人為設(shè)定，具有學(xué)習(xí)速度快、魯棒性好等優(yōu)點[14-16]。圖4中：x為輸入的軸承故障特征；y為模型輸出的軸承故障類型；ωi為第i個隱含神經(jīng)元的輸入權(quán)重；βi為第i個隱含神經(jīng)元的輸出權(quán)重；b為隨機獲得的隱含層偏置。

對于含有N1個樣本數(shù)據(jù)集，其中xi=[xi1，xi2，…，xin]T，ELM的網(wǎng)絡(luò)結(jié)構(gòu)為

式中：wi和βi分別為第i個隱含神經(jīng)元的輸入權(quán)重和輸出權(quán)重；bi和g分別為隨機獲得的隱含層偏置和激活函數(shù)，通常選取Sigmoid函數(shù)。

通過激活函數(shù)的選取以及隱含層節(jié)點確定后，ELM學(xué)習(xí)的步驟分為三步。

1） 初始化并隨機設(shè)定輸入權(quán)值w和隱含層偏置bi；

2） 計算隱含層輸出矩陣v；

3） 通過輸出的權(quán)重矩陣wo=vyi得到輸出權(quán)值。

3 基于IMSDE鐵路機車軸承故障診斷流程

針對鐵路機車軸承在真實復(fù)雜環(huán)境下故障特征難以提取而導(dǎo)致故障診斷困難的問題，本文提出一種IMSDE的鐵路機車軸承故障診斷方法。故障診斷流程分為三步。

1） 采集鐵路機車軸承7種不同健康狀態(tài)的振動信號。

2） 利用IMSDE提取軸承振動信號中包含的故障特征并構(gòu)成多維特征矩陣，然后對特征矩陣進行歸一化處理。其中IMSDE參數(shù)設(shè)置如下：符號數(shù)ε=8，嵌入維度m=3，尺度因子τ=[1，20]和時間延遲λ=1。

3） 將歸一化處理后的多維特征矩陣輸入到ELM模型中進行分類，實現(xiàn)對鐵路機車軸承故障的精準診斷。

4 試驗分析

為了測試IMSDE方法在實驗室數(shù)據(jù)和工程實測數(shù)據(jù)提取故障特征的效果，本節(jié)分別采用凱斯西儲大學(xué)軸承數(shù)據(jù)、南昌鐵路局機車軸承故障數(shù)據(jù)以及中車青島四方輪對軸承故障數(shù)據(jù)進行試驗分析。

4.1 凱斯西儲大學(xué)軸承數(shù)據(jù)試驗分析

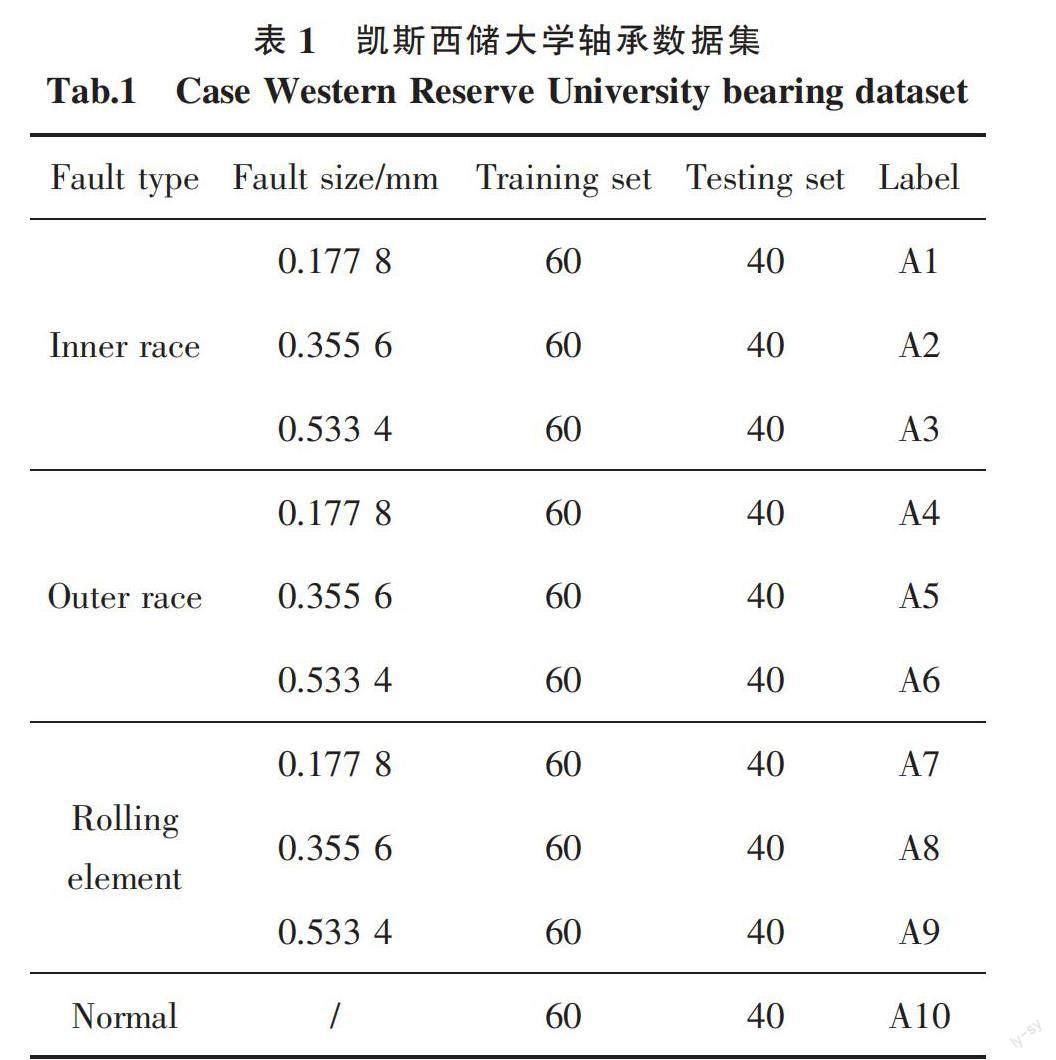
凱斯西儲大學(xué)試驗軸承型號為6205-2RS深溝型球軸承，安裝位置位于驅(qū)動端一側(cè)，采樣頻率為Fs=12 kHz。通過電火花加工出10種不同狀態(tài)的軸承數(shù)據(jù)，并將其依次編號A1～A10，如表1所示。

在凱斯西儲大學(xué)軸承數(shù)據(jù)集中共包含10種不同健康狀態(tài)數(shù)據(jù)，將每種狀態(tài)原始數(shù)據(jù)分為100組樣本，10種狀態(tài)共計1 000個完備樣本，每組樣本數(shù)據(jù)長度設(shè)置為1 024個樣本點。每種故障類型的數(shù)據(jù)樣本隨機取60個作為訓(xùn)練集，剩余的40個作為測試集。10種狀態(tài)下訓(xùn)練集總樣本數(shù)量為600，測試集總樣本數(shù)量400。分別計算其在20個尺度下IMSDE，得到大小分別為600×20訓(xùn)練集特征矩陣和400×20的測試集特征矩陣。

然后將訓(xùn)練集特征矩陣輸入到ELM模型中進行訓(xùn)練，將測試集特征矩陣輸入到訓(xùn)練完成的ELM模型中，得到單次試驗分類結(jié)果如圖5所示。

由圖5可知，采用凱斯西儲大學(xué)軸承數(shù)據(jù)數(shù)據(jù)集分析得到的單次的故障識別率為100%，初步驗證了所提方法能夠有效識別滾動軸承的不同故障類型與程度。

為避免實驗存在的偶然性情況，使獲得的實驗結(jié)果更具權(quán)威性，將所有樣本隨機劃分后進行了20次隨機試驗，并與MSDE、改進多尺度排列熵（IMPE）[17]、改進多尺度樣本熵（MMSE）[18]進行對比，試驗結(jié)果如表2所示。

可以看出，本文所提方法所獲得的平均識別準確率最高，最大識別準確率為100%，最小識別準確率為99%，前后者之間相差1%，再次證明了所提方法具較優(yōu)的故障識別能力。

4.2 南昌鐵路局機車軸承故障數(shù)據(jù)試驗分析

本節(jié)所使用的軸承數(shù)據(jù)來自南昌鐵路局機務(wù)段的JL-501機車軸承試驗臺。試驗臺的主要由臺身、主軸箱、液壓系統(tǒng)、電氣系統(tǒng)組成，如圖6所示。主軸箱用于安裝定位、旋轉(zhuǎn)等過程；液壓系統(tǒng)的功能為徑向載荷的施加和卸載，本次試驗轉(zhuǎn)速設(shè)定為500 r/min。DF4型內(nèi)燃機車所采用的軸承型號為NJ2232WB系列圓柱滾子軸承。如圖5所示，加速度傳感器A、B、C位于3個不同位置，用于多方位采集機車軸承信號，采樣頻率為20 kHz。采用振動傳感器B采集7種不同狀態(tài)的機車軸承真實損傷數(shù)據(jù)，并將其依次編號B1～B7，如表3所示。6種機車軸承不同程度的真實損傷如圖7所示。

在南昌鐵路局機車軸承故障數(shù)據(jù)集中共包含7種不同健康狀態(tài)數(shù)據(jù)，將每種狀態(tài)原始數(shù)據(jù)分為100組樣本，7種狀態(tài)共計700個完備樣本，每組樣本數(shù)據(jù)長度設(shè)置為1 024個樣本點。每種故障類型的數(shù)據(jù)樣本隨機取60個作為訓(xùn)練集，剩余的40個作為測試集。7種狀態(tài)下訓(xùn)練集總樣本數(shù)量為420，測試集總樣本數(shù)量280。分別計算其在20個尺度下IMSDE，得到大小分別為420×20訓(xùn)練集特征矩陣和280×20的測試集特征矩陣。

然后將訓(xùn)練集特征矩陣輸入到ELM模型中進行訓(xùn)練，將測試集特征矩陣輸入到訓(xùn)練完成的ELM模型中，得到單次試驗分類結(jié)果如圖8所示。

由圖8可知，采用南昌鐵路局機車軸承故障數(shù)據(jù)集分析得到的單次的故障識別率為97.5%，初步驗證了所提方法能夠有效識別滾動軸承的不同故障類型與程度。

為避免實驗存在的偶然性情況，使獲得的實驗結(jié)果更具權(quán)威性，將所有樣本隨機劃分后進行了20次隨機試驗，并與MSDE、IMPE、MMSE進行對比，試驗結(jié)果如表4所示。

可以看出，本文所提方法所獲得的平均識別準確率最高，相比于MSDE、IMPE以及MMSE方法的分別提升了22.27%，10.63%，15.92%。

4.3 青島四方輪對軸承故障數(shù)據(jù)試驗分析

青島四方輪對軸承試驗臺如圖9所示，試驗臺主要由驅(qū)動電機、皮帶傳動系統(tǒng)、徑向加載裝置、橫向加載裝置、風(fēng)扇電機以及控制裝置組成。其采樣頻率為20 kHz，車輛運行速度為90 km/h，軸承轉(zhuǎn)速為589 r/min，垂向載荷為146 kN。

真實產(chǎn)生的故障類型一共8種，將其依次編號C1～C8，如表5所示。7種輪對軸承全生命周期運行過程中產(chǎn)生的不同程度損傷如圖10所示。

同樣地，將8種狀態(tài)原始數(shù)據(jù)分為100組樣本，10種狀態(tài)共計800個完備樣本，每組樣本數(shù)據(jù)長度設(shè)置為1 024個樣本點。每種故障類型的數(shù)據(jù)樣本隨機取60個作為訓(xùn)練集，剩余的40個作為測試集。8種狀態(tài)下訓(xùn)練集總樣本數(shù)量為480，測試集總樣本數(shù)量320。分別計算其在20個尺度下IMSDE，得到大小分別為480×20訓(xùn)練集特征矩陣和320×20的測試集特征矩陣。

然后將訓(xùn)練集特征矩陣輸入到ELM模型中進行訓(xùn)練，將測試集特征矩陣輸入到訓(xùn)練完成的ELM模型中，得到單次試驗分類結(jié)果如圖11所示。

由圖11可知，采用青島四方輪對軸承故障數(shù)據(jù)集分析得到的單次的故障識別率為98.4%，初步驗證了所提方法能夠有效識別滾動軸承的不同故障類型與程度。

為避免實驗存在的偶然性情況，使獲得的實驗結(jié)果更具權(quán)威性，將所有樣本隨機劃分后進行了20次隨機試驗，并與MSDE、IMPE、MMSE進行對比，試驗結(jié)果如表6所示。

可以看出，本文所提方法所獲得的平均識別準確率最高，相比于MSDE，IMPE以及MMSE方法的分別提升了44.76%，1.06%，6.22%。不同試驗數(shù)據(jù)產(chǎn)生的結(jié)果具有一定的差異，相比于凱斯西儲大學(xué)軸承數(shù)據(jù)，青島四方軸承故障數(shù)據(jù)獲得識別準確率較低。可能的原因是由于凱斯西儲大學(xué)軸承數(shù)據(jù)集是采用電火花方式構(gòu)造出人工故障，其缺陷處較為光滑與平整，而青島四方軸承故障數(shù)據(jù)是工程實際產(chǎn)生的軸承故障，其缺陷處具有不規(guī)則形狀，所以故障識別率低于人工構(gòu)造的軸承故障。

5 結(jié)論

1） 在多尺度符號動力學(xué)熵（MSDE）的基礎(chǔ)上，提出了一種改進多尺度符號動力學(xué)熵（IMSDE）的方法。然后通過信號的仿真分析，確定了IMSDE參數(shù)選擇的標準。將IMSDE與MSDE進行對比，結(jié)果表明IMSDE能夠準確表達信號時間序列的動力學(xué)變換，解決了傳統(tǒng)時間序列的粗粒化會導(dǎo)致時間序列長度急劇縮短的問題，提升了提取大尺度因子下的粗粒化序列關(guān)鍵故障特征的能力。

2） 采用IMSDE的方法應(yīng)用于3組數(shù)據(jù)分析，結(jié)果表明對實驗室構(gòu)造的軸承故障，由于其缺陷處較為光滑與平整，振動信號噪聲較少，故障識別平均準確率達到99%以上。對于工程實際產(chǎn)生的軸承故障，其缺陷處具有不規(guī)則形狀，振動信號噪聲較高，故障識別平均準確率達到95%以上，驗證了該方法具有一定工程實際應(yīng)用價值。

3） 通過3種特征提取方法對軸承不同故障類型識別結(jié)果的對比分析，進一步驗證了IMSDE不僅能夠有效提取軸承的故障信息，還能夠?qū)Σ煌收铣潭鹊奶卣鬟M行提取。與MSDE相比，IMSDE能夠更全面、更豐富的提取故障信息。與IMPE、MMSE相比，IMSDE能夠通過符號化的過程實現(xiàn)更加穩(wěn)定的特征提取效果。

參考文獻：

[1] 張龍，彭小明，熊國良，等. 基于MSE與PSO-SVM的機車輪對軸承智能診斷方法[J]. 鐵道科學(xué)與工程學(xué)報，2021，18（9）：2408-2417.

ZHANG L，PENG X M，XIONG G L，et al. Intelligent diagnosis of locomotive wheelset bearings using MSE and PSO-SVM[J]. Journal of Railway Science and Engineering，2021，18（9）：2408-2417.

[2] LIU W，YANG S，LI Q，et al. The mkurtogram：A novel method to select the optimal frequency band in the AC domain for railway wheelset bearings fault diagnosis[J]. Applied Sciences，2020，11（1）：9.

[3] 卓鵬程，嚴瑾，鄭美妹，等. 面向滾動軸承全生命周期故障診斷的GA-OIHF Elman神經(jīng)網(wǎng)絡(luò)算法[J]. 上海交通大學(xué)學(xué)報，2021，55（10）：1255-1262.

ZHUO P C，YAN J，ZHENG M M，et al. GA-OIHF Elman network algorithm for fault diagnosis of full life cycle of rolling bearing[J]. Journal of Shanghai Jiaotong University，2021，55（10）：1255-1262.

[4] LI Y，YANG Y，LI G，et al. A fault diagnosis scheme for planetary gearboxes using modified multi-scale symbolic dynamic entropy and mRMR feature selection[J]. Mechanical Systems and Signal Processing，2017，91：295-312.

[5] 姚德臣，楊建偉，程曉卿，等. 基于多尺度本征模態(tài)排列熵和SA-SVM的軸承故障診斷研究[J]. 機械工程學(xué)報，2018，54（9）：168-176.

YAO D C，YANG J W，CHENG X Q，et al. Railway rolling bearing fault diagnosis based on muti-scale IMF permutation entropy and SA-SVM classifier[J]. Journal of Mechanical Engineering，2018，54（9）：168-176.

[6] YANG Y，ZHENG H，YIN J，et al. Refined composite multivariate multiscale symbolic dynamic entropy and its application to fault diagnosis of rotating machine[J]. Measurement，2020，151：107233.

[7] 王斐，房立清，齊子元. 基于多尺度樣本熵和VPMCD的自動機故障診斷[J]. 振動.測試與診斷，2018，38（3）：564-569.

WANG ，F(xiàn)ANG L Q，QI Z Y. Automatic machine fault diagnosis based on multi-scale sample entropy and VPMCD[J]. Journal of Vibration，Measurement & Diagnosis，2018，38（3）：564-569.

[8] 鄭近德，程軍圣，楊宇. 多尺度排列熵及其在滾動軸承故障診斷中的應(yīng)用[J]. 中國機械工程，2013，24（19）：2641-2646.

ZHENG J D，CHENG J S，YANG Y. Multi-scale permutation entropy and its applications to rolling bearing fault diagnosis[J]. China Mechanical Engineering，2013，24（19）：2641-2646.

[9] LI Y，LIANG X，WEI Y，et al. A method based on refined composite multi-scale symbolic dynamic entropy and

ISVM-BT for rotating machinery fault diagnosis[J]. Neurocomputing，2018，315：246-260.

[10] 陳祥龍，張兵志，馮輔周，等. 基于改進排列熵的滾動軸承故障特征提取[J]. 振動工程學(xué)報，2018，31（5）：902-908.

CEHN X L，ZHANG B Z，F(xiàn)ENG F Z，et al. Fault feature extraction of rolling bearings based on an improved permutation entropy[J]. Journal of Vibration Engineering，2018，31（5）：902-908.

[11] 李永波. 滾動軸承故障特征提取與早期診斷方法研究[D]. 哈爾濱：哈爾濱工業(yè)大學(xué)，2017.

LI Y B. Investigation of fault feature extraction and early fault diagnosis for rolling bearings[D]. Harbin：Harbin Institute of Technology，2017.

[12] HAN M，WU Y，WANG Y，et al. Roller bearing fault diagnosis based on LMD and multi-scale symbolic dynamic?information entropy[J]. Journal of Mechanical Science and?Technology，2021，35（5）：1993-2005.

[13] COSTA M，GOLDBERGER A L，PENG C K. Multiscale entropy analysis of biological signals[J]. Physical Review E，2005，71（2）：021906.

[14] HUANG G B，WANG D H，LAN Y. Extreme learning machines[J]. International Journal of Machine Learning and Cybernetics，2011，2（2）：107-122.

[15] HE C，WU T，GU R，et al. Rolling bearing fault diagnosis based on composite multiscale permutation entropy and reverse cognitive fruit fly optimization algorithm-extreme?learning machine[J]. Measurement，2021，173：108636.

[16] 周建民，劉露露，楊曉彤，等. 自編碼器及其改進算法在滾動軸承故障診斷的應(yīng)用[J]. 華東交通大學(xué)學(xué)報，2023，40（3）：88-96.

ZHOU J M，LIU L L，YANG X T，et al. Application of Auto-Encoder and Its Improvement in Rolling Bearing Fault Diagnosis[J]. Journal of East China Jiaotong University，2023，40（3）：88-96.

[17] LI Y，ZHANG W，XIONG Q，et al. A rolling bearing fault diagnosis strategy based on improved multiscale permutation entropy and least squares SVM[J]. Journal of Mechanical Science and Technology，2017，31（6）：2711-2722.

[18] MAHAJAN R，MORSHED B I. Unsupervised eye blink artifact denoising of EEG data with modified multiscale sample entropy，kurtosis，and wavelet-ICA[J]. IEEE journal of Biomedical and Health Informatics，2014，19（1）： 158-165.

通信作者：張龍（1980—），男，教授，博士，研究方向為裝備服役性能監(jiān)測、診斷與智能運維。E-mail：longzh@126.com。

（責(zé)任編輯：姜紅貴）