柔性壁擴張式消聲器的消聲性能分析及優化

劉曉昂,韓子康,李 浩,甄 冉,李來鑫,上官文斌

(1.河北工業大學 機械工程學院 天津市新能源汽車動力傳動與安全技術重點實驗室,天津 300130;2.河北工業大學 化工學院,天津 300130;3.山東美晨工業集團有限公司,山東 濰坊 262200;4.華南理工大學 機械與汽車工程學院,廣州 510641)

汽車在生活中的大量應用帶來了顯著的噪聲問題,給人們的日常生活造成了很大影響。在汽車產生的各類噪聲中,進氣噪聲不僅是車外噪聲的主要組成部分,也是汽車駕駛艙的主要噪聲源之一,因此對進氣噪聲進行控制十分重要[1]。進氣系統噪聲的主要控制方式為安裝消聲器,這其中又以抗性擴張式消聲器耐氣流沖擊、結構簡單等特點而被廣泛應用。

基于抗性擴張式消聲器,研究人員多以傳遞損失為評價指標[2],對具有不同結構特點的擴張式消聲器消聲性能進行分析或優化。左曙光等[3]利用二維解析方法研究了兩腔抗性消聲器的聲學性能,得出了不同結構參數影響消聲器傳遞損失的主次關系;Almeida等[4]引入聲子晶體概念設計了一種擴張腔周期排布式消聲器并對擴張腔的尺寸進行了優化調整,得到了較好的消聲效果;Lee等[5]以消聲器內部的分區體積做為優化變量,對消聲器進行了基于噪聲頻率和噪聲溫度不確定性的優化,并通過試驗驗證了優化后消聲器的噪聲衰減性能;Li等[6]考慮消聲器腔室間的耦合效應,研究了關鍵結構參數對消聲器腔室耦合效應的影響,并在此基礎上對結構參數進行了優化,提升了消聲性能;Fu等[7]研究了不同結構設計參數下消聲器的傳遞損失,為消聲器結構參數的設計提供了理論依據;劉志恩等[8]提出了一種多腔微穿孔管消聲器結構,并采用遺傳算法對多腔微穿孔管消聲器的結構參數進行了優化設計,得到了較好的消聲效果。呂傳茂等[9]設計了一種亥姆霍茲消聲器,采用遺傳算法對亥姆霍茲消聲器的結構參數進行了優化并進行了試驗驗證,證明了優化結果的有效性。

綜上所述,研究人員主要就擴張式消聲器結構參數與傳遞損失之間的關系進行了探討及優化,這表明了消聲器開發過程中結構參數的重要作用,但這些研究均基于消聲器剛性壁條件,目前已有研究人員指出了聲固耦合效應在柔性壁消聲器設計中起到的重要作用[10]。在汽車內部空間越發有限的前提下,基于剛性壁擴張式消聲器所進行的結構參數調整越來越難以滿足汽車的降噪要求,而考慮聲固耦合效應的柔性壁擴張式消聲器與剛性壁擴張式消聲器相比,可調的結構參數增添了材料的彈性模量和壁厚兩項,且所述結構參數的調整不影響消聲器的外部尺寸,利用聲固耦合效應對柔性壁擴張式消聲器進行設計優化是一條新出路。

考慮聲固耦合效應,趙曉臣等[11]以應用于空氣輸運系統的鼓型消聲器為研究對象,分析了膜片位置、單雙腔等結構因素對鼓型消聲器聲學性能的影響;何濤等[12]研究了彈性板式消聲器聲振特性與消聲性能,為艦船水管路的消聲設計提供了理論基礎。然而,較少有看到關于柔性壁擴張式消聲器在車用進氣管路中應用的詳細報道,且在以往的研究中,針對消聲器的結構參數,研究人員多進行了評價指標下的單因素分析,較少對結構因素之間的主次關系進行研究,而分析結構因素間的主次關系可以為消聲器的優化設計提供重要優化方向。因此,本文將柔性壁擴張式消聲器應用于車輛進氣管路系統,并開展了以下研究：首先,建立了柔性壁擴張式消聲器的解析模型,與有限元計算結果對比,驗證建立模型的正確性;然后,給出了消聲器分別在剛性壁及柔性壁條件下的傳遞損失曲線,肯定了聲固耦合效應對消聲器傳遞損失的影響;設計正交試驗,得到了影響消聲器傳遞損失性能的結構因素之間的主次關系;采用遺傳算法對所設計消聲器進行優化,與優化前消聲器傳遞損失進行對比,驗證優化方案的有效性;最后,采用有限元法對優化后柔性壁擴張式消聲器的耐進氣管路負壓性能進行了分析,驗證了所設計消聲器在進氣管路系統中具有較好的適用性。研究為車用進氣管路領域擴張式消聲器的設計與性能分析提供了新思路與新方法,可為相關工作提供參考。

1 柔性壁擴張式消聲器聲固耦合模型

柔性壁擴張式消聲器模型如圖1所示。

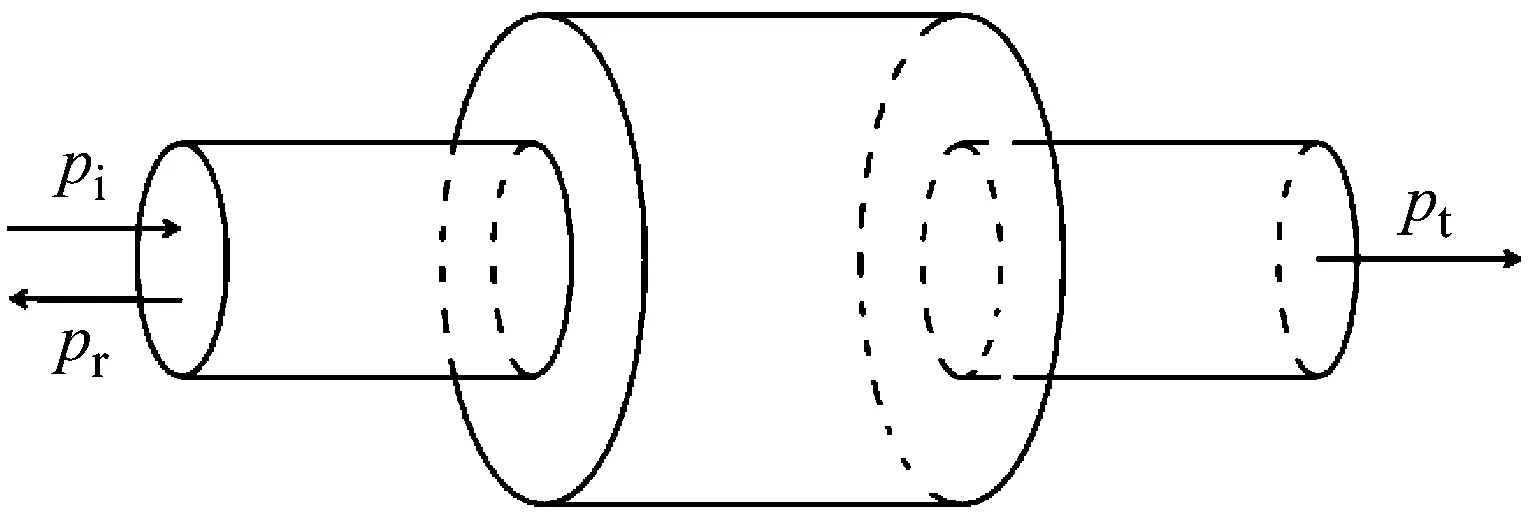
(a) 消聲器三維結構

如圖1所示：消聲器擴張腔長度為L;進出口半徑為R1;擴張腔半徑為R2;柔性壁壁厚為e;pi為入射波聲壓;pr為反射波聲壓;pt為透射波聲壓。

參考文獻[13-14]中提到的相關理論,在擴張腔上,基于一維平面波理論,設激勵源總聲壓為P,振速為V,消聲器軸向為z向,介質密度為ρ,時間為t,在軸向上介質流體有動量方程

(1)

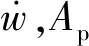
(2)

根據廣義胡克定律得到擴張腔固體的幾何物理方程

(3)

式中：ν為泊松比;E為彈性模量。根據流體連續方程,結合聲固交界面法向振速聲壓連續條件得到耦合方程

(4)

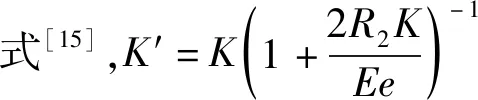
2 解析模型的求解與驗證

2.1 模型的求解方法

2.1.1 場傳遞矩陣

引用張立翔等的求解思路,將式(1)～式(4)利用拉氏變換從時域轉換到頻域上進行求解。令

(5)

式中：y(z,t)為4×1矩陣,其中的4個參數分別代表流體振速、聲壓、消聲器固體振速、消聲器軸向上所受內力,結合式(5)可將式(1)～式(4)寫為如下矩陣形式

(6)

式中,A,B,C均為4×4的系數矩陣,對式(6)進行拉氏變換,經過推導可得

(7)

V-1·Δ·V=T

(8)

T=diag[λ1,λ2,λ3,λ4]

(9)

式中,λ1～λ4為T矩陣的4個特征值,將式(9)代入式(7)推導得

(10)

r(z,s)=E(z,s)·r0(z,s)

(11)

式中,r0(z,s)為待定向量,其值需結合邊界條件進行計算,E(z,s)表達式如下

(12)

在消聲器入口,z=0,此時E(0,s)為單位陣,將其代入式(11)中得

(13)

將式(13)進行整理得

(14)

2.1.2 點傳遞矩陣

對于本文消聲器來說,為方便接下來的公式推導,分別用下標1,2,3代表消聲器的進口段、擴張腔段以及出口段。狀態向量傳遞進入消聲器擴張腔時,據聲壓以及體積速度連續條件求得狀態向量的點傳遞矩陣為

式中,Al為流體域的橫截面積,同理可得到狀態向量從擴張腔傳入出口段的點傳遞矩陣φ2。

因此,狀態向量進出擴張腔的點傳遞矩陣分別為φ1,φ2,入口段、擴張腔段、出口段的場傳遞矩陣分別為U1,U2,U3,此時總傳遞矩陣為Uall=U3U2U1。

2.1.3 邊界約束矩陣與激勵矩陣

在入口處給流體施加1 m/s的階躍振速信號,根據力平衡方程結合式(5)得到消聲器入口處的邊界約束矩陣D1與激勵矩陣F1如下

消聲器出口為無反射出口條件,聲阻抗等于流體的特性阻抗,設介質中聲速為c,對本文消聲器來說有

(15)

出口處無聲源激勵,結合式(15)得到出口處的邊界約束矩陣D3與激勵矩陣F3

2.1.4 消聲器的傳遞損失

基于2.1.3節推導可得

(16)

(17)

聯立式(16)、式(17),可求得消聲器入口處的狀態向量

(18)

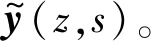
基于一維平面波理論,傳遞損失[16]定義表示為

LT=10lg(Wi-Wt)

(19)

式中：LT為傳遞損失;Wi和Wt分別為消聲器入口處的入射聲功率和出口處的透射聲功率。Wi和Wt可表示為

(20)

(21)

式中：S為橫截面積;pi與pt分別為入射波與透射波聲壓。

將式(19)、式(20)代入式(18),在消聲器進出口橫截面積相同,介質相同條件下可整理為如下形式

(22)

根據聲學理論,將本文參數代入式(21)推導得傳遞損失為

(23)

2.2 解析模型的驗證

計算時參數取值如表1所示。

表1 參數取值

為驗證解析模型的正確性,分別采用解析法與有限元法兩種方式對柔性壁擴張式消聲器的傳遞損失進行計算。在有限元軟件COMSOL中選用聲-固耦合模塊計算柔性壁擴張式消聲器的傳遞損失。

消聲器外殼區域為聲-固耦合面,在軟件里選中該耦合面打開多物理場耦合開關,激活耦合面處的振速及聲壓連續條件,同時,按照表1中所示的取值對兩種方法下的柔性壁面結構參數進行設置,從而使兩種方法在計算時具有較好的一致性。網格劃分尺寸選為2～5 mm,在入口處給流體施加1 m/s的階躍振速信號。按照表1中取值進行計算,解析法與有限元法結果對比如圖2所示。圖2中可見兩種方法結果吻合良好,在高頻帶范圍內差值逐漸變大是因為解析法模型基于一維平面波理論,而在高頻段消聲器內部出現了高次波;兩種方法所得傳遞損失峰值在低頻處的差異來源于解析法未對柔性壁的阻尼進行考慮。總體誤差可接受,驗證了所建立模型的正確性。

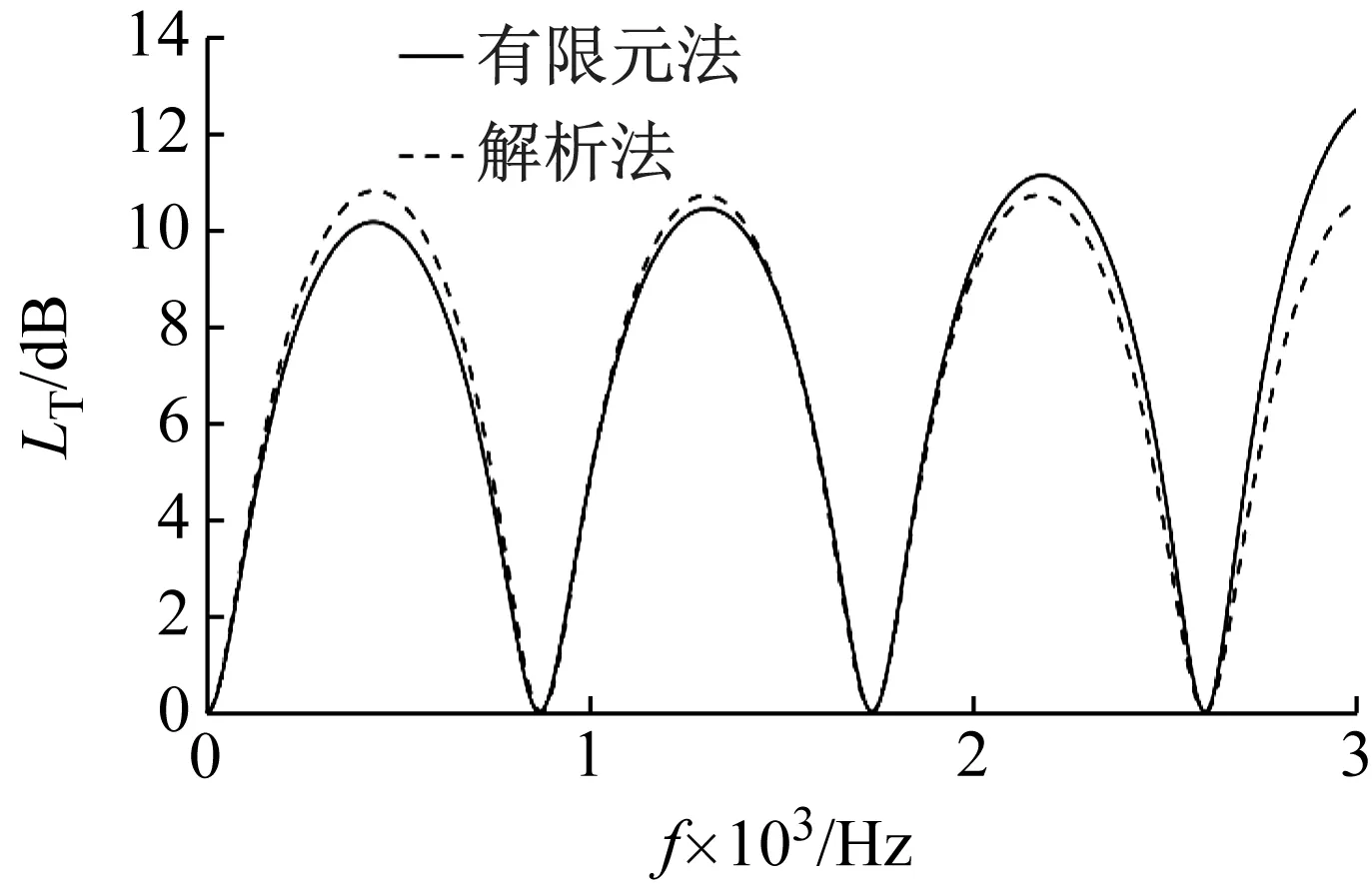
圖2 不同方法結果對比

3 影響消聲器傳遞損失性能的結構因素主次分析

3.1 聲固耦合效應對消聲器傳遞損失的影響

消聲器在剛性壁條件與柔性壁條件下的傳遞損失如圖3所示。

圖3 有無耦合傳遞損失曲線對比

如圖3所示,在柔性壁條件下,消聲器傳遞損失峰值頻率向低頻移動,峰值提升。以下見表2,給出剛性壁與柔性壁條件下聲模態前6階特征頻率對此現象進行說明。

表2 不同條件下聲模態前6階特征頻率

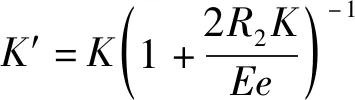
3.2 正交試驗設計

消聲器的傳遞損失性能只與結構有關,實際應用中結構參數之間可能存在多種組合,因此,本文設計了正交試驗探討結構因素之間影響柔性壁擴張式消聲器傳遞損失性能的主次關系,為柔性壁擴張式消聲器的設計與優化提供參考。消聲器擴張比定義為擴張腔半徑與進出口段半徑的比值,本文將擴張腔長度、擴張比、柔性壁彈性模量、柔性壁壁厚作為考慮因素,每個因素選取4個水平進行分析,分別以A,B,C,D代表擴張腔長度、柔性壁壁厚、柔性壁彈性模量、擴張比。因素水平表設置如表3所示。

表3 消聲器正交試驗設計因素水平表

3.3 正交試驗結果及極差分析

基于表3進行計算,以消聲器在0～3 kHz內的傳遞損失峰值以及在不同頻段內的傳遞損失平均值為評價指標,結果如表4所示。

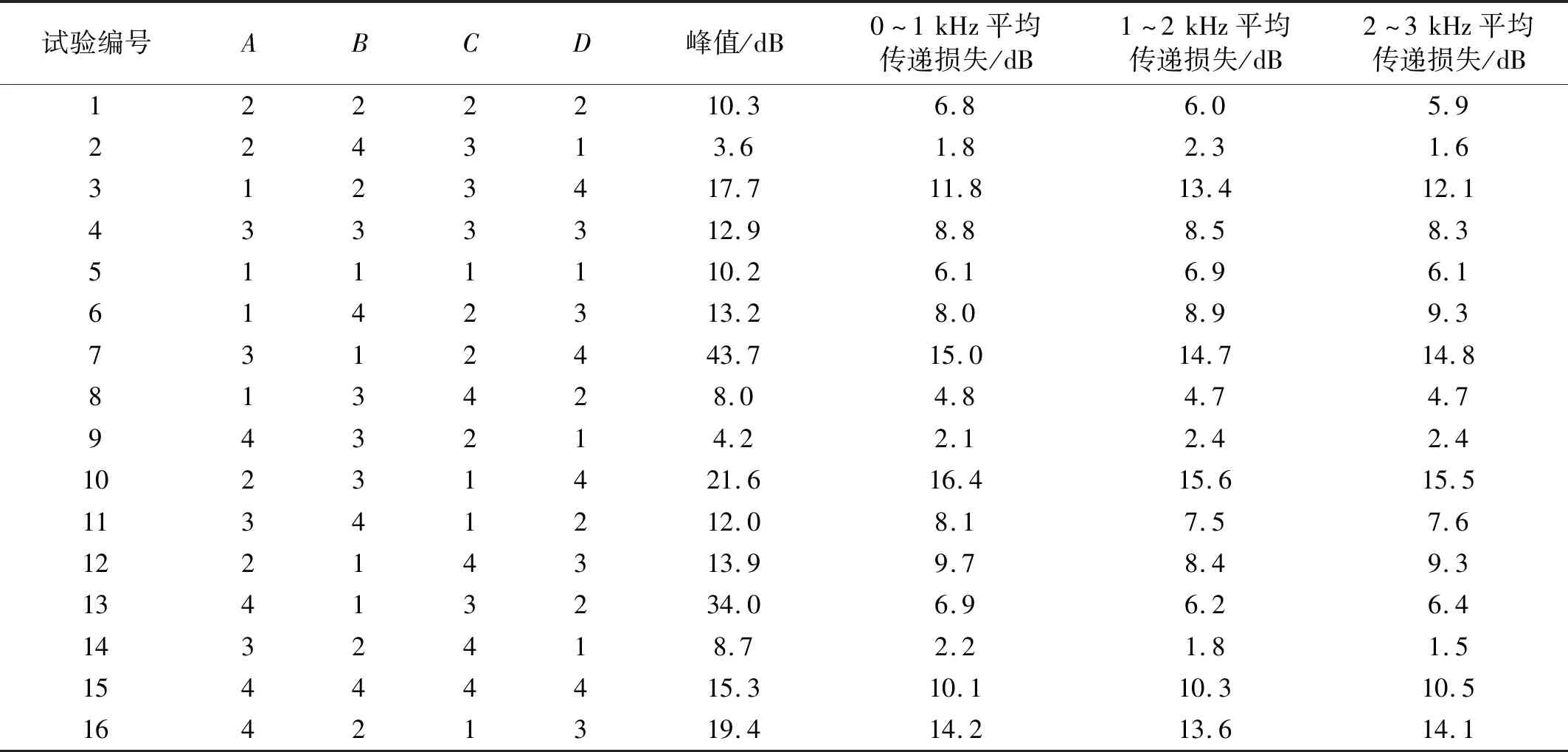
表4 消聲器正交試驗結果

對于正交試驗結果,本文采用極差分析,通過計算各因素的極差值Y分析各因素間的主次關系。極差的計算公式如下

(24)

(25)

Gi=∑hi

(26)

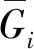
以傳遞損失峰值為例進行說明,以傳遞損失峰值為目標的極差分析見表5。

表5 以傳遞損失峰值為目標的極差分析表

影響消聲器傳遞損失的結構因素主次可通過極差大小來辨別,表5中,影響消聲器傳遞損失性能的結構因素主次排序為擴張比、柔性壁壁厚、擴張腔長度、柔性壁彈性模量。使消聲器傳遞損失峰值取得最大值的結構參數最優組合為擴張腔長度0.25 m,壁厚0.000 3 m,彈性模量20 MPa,擴張比3。

基于正交試驗結果,將評價指標下極差最小值結構因素看做單位1,給出結構因素在不同評價指標下的表現,如圖4所示。

圖4 結構因素對消聲性能的影響

由圖4可見：在不同評價指標下,消聲器擴張比均為主要影響因素;柔性壁彈性模量主要影響除傳遞損失峰值之外的評價指標;擴張腔長度對4個評價指標影響均較小。除去消聲器擴張比,在傳遞損失峰值評價指標下,第二影響因素為柔性壁壁厚;在其余3個評價指標下,第二影響因素為柔性壁彈性模量。

4 消聲器結構參數的優化設計

4.1 目標函數

據3.3節主次因素分析,消聲器擴張腔長度對4個評價指標影響均較小。因此,優化時為簡化計算量可只取消聲器擴張比、彈性模量、壁厚3個結構因素進行分析,取消聲器在0～3 kHz內的傳遞損失峰值與3個頻率區間內的傳遞損失平均值權重各為0.25,設置目標函數為

(27)

式中：LTP為傳遞損失峰值;LTiave為傳遞損失在0～1 kHz,1～2 kHz,2～3 kHz內的傳遞損失平均值。

4.2 優化結果及對比

以消聲器擴張比、柔性壁壁厚、柔性壁彈性模量為優化變量,選用遺傳算法進行優化,優化前后結構參數取值及取值范圍如表6所示。

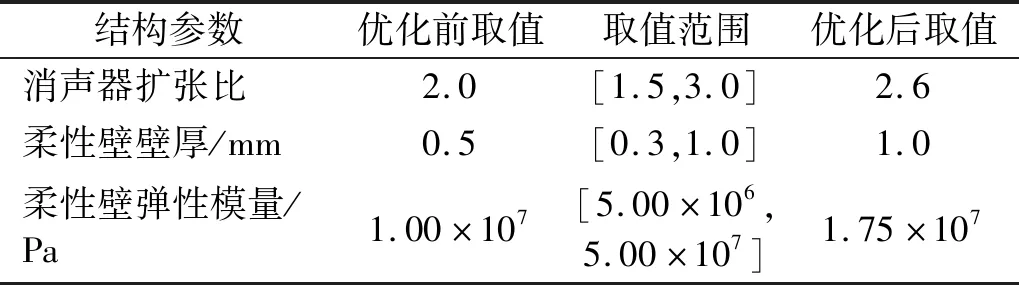
表6 結構參數優化前后取值及取值范圍

在該優化方案下,優化前后柔性壁擴張腔式消聲器傳遞損失性能對比如表7所示。

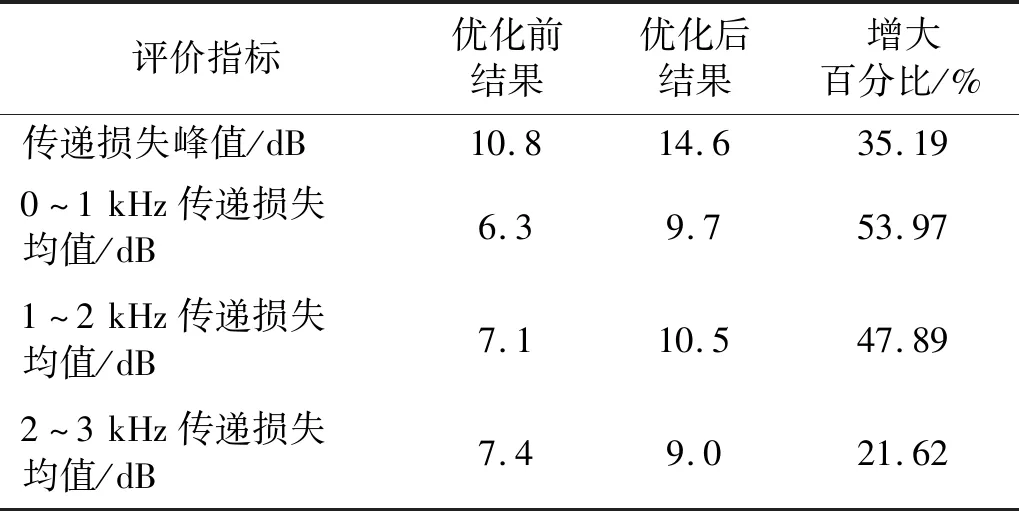
表7 優化前后評價指標值

由表6、表7可見,本文提出的優化方案使消聲器各評價指標下的消聲性能均得到了提升。優化前后消聲器傳遞損失均值增幅在0～1 kHz,1～2 kHz,2～3 kHz內依次遞減,表明優化后消聲器的低頻消聲性能得到了更好的提升。根據絕對數值來看,優化后消聲器在各頻段的消聲能力趨于一致。

5 消聲器耐負壓性能驗證

由于所設計消聲器應用對象為車用進氣管路,因此有必要考慮所設計消聲器的耐負壓性能。網格劃分尺寸為2 mm。

以某在研發型號進氣管路為例,裝配該管路的車型在怠速狀態下的最大進氣負壓為60 kPa,技術要求在該負壓下,管路形變率小于10%。在有限元軟件ANSYS中進行計算得到形變云圖,如圖5所示。

圖5 60 kPa負壓下的消聲器形變云圖

由圖5可見,在60 kPa負壓下,所設計柔性壁擴張式消聲器的單側最大形變為2.93 mm,由于消聲器為軸對稱結構,則雙側最大形變為5.86 mm。與消聲器擴張腔橫截面直徑相比,最大形變率為5.63%,符合設計要求。實際消聲器在使用時形變率會在0%～5.63%區間內往復振動,此時消聲器的最小擴張比為2.45,給出當優化后的消聲器擴張比變為2.45時,考慮負壓與否對消聲器消聲性能的影響,如表8所示。

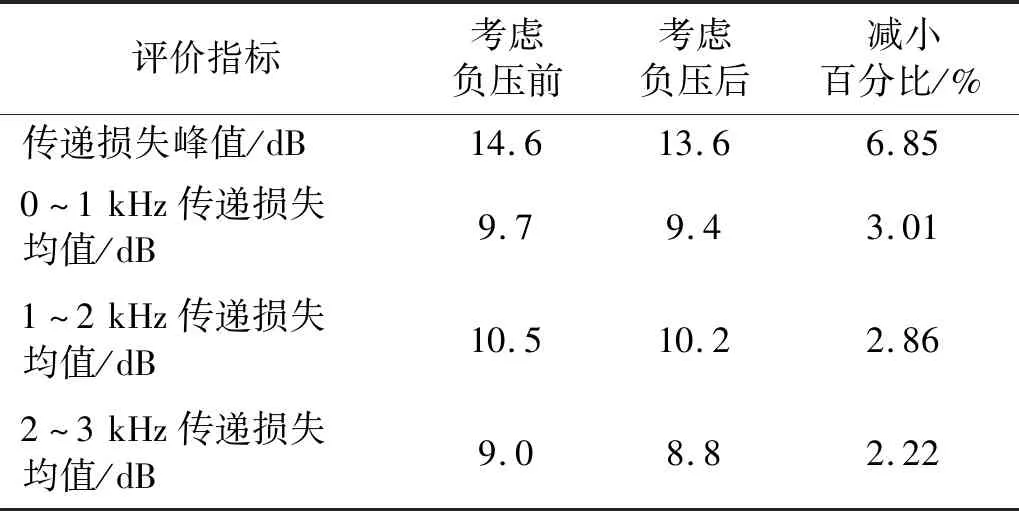
表8 考慮負壓前后評價指標值

由表8可見,考慮負壓后各評價指標下的消聲性能均有一定幅度的降低,但仍然要高于優化前消聲器的消聲性能。然而,擴張比為2.45的區域只占擴張腔的一小部分,消聲器的平均擴張比要大于2.45,所以實際上的消聲性能降低幅度更小,且車輛大多數時候處于行駛狀態,進氣負壓遠小于怠速狀態,消聲器最大形變也會小于5.86 mm。因此,綜上考慮,認為考慮進氣管路負壓時的消聲器消聲性能不會受到較大影響,所設計消聲器在車用進氣管路中具有良好的適用性。

6 結 論

(1) 基于一維平面波理論建立了聲固耦合解析模型,該模型擁有較高的精度。

(2) 與剛性壁消聲器對比,柔性壁消聲器的傳遞損失峰值頻率降低且峰值提高。

(3) 基于正交試驗探討了柔性壁擴張式消聲器結構因素與傳遞損失性能之間的關系,結果表明：在不同評價指標下,消聲器擴張比均為最主要影響因素,除去消聲器擴張比,影響傳遞損失峰值的第二結構因素為柔性壁壁厚,影響傳遞損失均值的第二結構因素為柔性壁彈性模量;擴張腔長度對4個評價指標影響均較小。

(4) 對所設計柔性壁擴張式消聲器的結構參數進行了優化,對比了不同評價指標在優化前后的值,結果表明：優化后消聲器的低頻消聲性能得到了更好的提升。根據絕對數值來看,優化后消聲器在各頻段的消聲能力趨于一致。

(5) 采用有限元的方式對所設計消聲器的耐負壓性能進行了分析,驗證了所設計消聲器在進氣管路中具有良好的適用性。