脈動環狀流作用下輸流管道的非線性振動特性分析

周云龍,米列東

(東北電力大學 能源與動力工程學院,吉林 吉林 132012)

隨著國民經濟的快速發展,輸流管道系統在石油、化工、電力等行業起著至關重要的作用。然而,因內部流體的流動引起的管道振動現象普遍存在。當管內流體的流速達到一定值時,管道結構會變得不穩定甚至破壞[1-2]。顯然,管道振動特性與其流體的流動特性密切相關。對于環狀流,氣、液兩相介質的速度相差幾十倍甚至數百倍且液膜厚度很小而常被忽視。然而,液、氣的密度相差數百倍,進而使得液、氣兩相速度歸一化后相差無幾,但二者的單位長度質量相差很大。此外,管道系統會因管內流體的脈動產生參數共振等豐富的動力學變化。因此,對液相速度及其脈動特性引起管道的振動特性變化的研究是至關重要的。

輸流管道振動是典型的流固耦合問題。近幾十年諸多學者做了大量的研究。Liang等[3]對旋壓流體輸流管道進行了大量的研究,結果表明當管內流體的流速達到臨界值時管道發生失穩。Yang等[4-5]分析了輸流管道振動特性。梁峰等[6]研究了外部周期激勵下兩端固定輸流管道伴隨內共振的非線性受迫振動問題。柳博瀚等[7]探討了管內流動對海洋柔性管道振動的影響。孟丹等[8]對管內流動和管外流動共同作用下的管道振動特性進行了研究。這些學者都關注單相流輸送管道共振參數問題,并且指出隨著液速的增加,管道固有頻率降低。

工程上,氣液混輸的現象十分普遍。多相流誘導的管道振動受到了廣泛關注。Liu等[9]指出管道在段塞流態下振動最大。Miwa等[10]對流致振動進行了細致的總結并指出在段塞流和環狀流態下管道振動明顯,同時強烈建議應重點關注環狀流的流致振動特征。Riverin等[11]在11種試驗條件對U型接頭和T型接頭進行應力測試,結果表明應力與兩相流過程中截面內氣體含量的變化有關。Liu等[12-13]對水平氣-液段塞流輸流管道固有頻率進行了研究,結果表明固有頻率受段塞流間歇性影響較大,固有頻率呈現間歇性變化。Ortiz-Vidal等[14]認為兩相流的流動參數直接影響振動特性。劉剛等[15]對環狀流管道振動模型進行了研究,并分析了固有頻率的變化情況。

在工程應用過程中由于泵、風機等動力設備的不穩定導致輸送的介質產生脈動。已有的文獻表明,兩端簡支的輸流直管系統在脈動流的作用下管道會出現參數共振[16-18]。在工程應用過程中由于泵、風機等動力設備的不穩定導致輸送的介質產生脈動。此外,對于多相流輸流管道,管道內各相介質沿管線的流速并不是恒定的。為了便于計算,常采用“One-dimensional channel flow”理論計算管道內流體的流動參數[19]。

基于上述研究,有一些細節值得注意。在以往的研究中主要關注穩定的氣液兩相環狀流水平管的振動特性。然而,液相介質的脈動將會引起管道系統非線性振動更加復雜,產生包括分岔、混沌等振動形態。因此,本文著重考慮在脈動的液相介質作用下,環狀流輸流管道的非線性振動特性。采用“One-dimensional channel flow”理論計算環狀流輸流管道內氣、液相介質的速度及單位長度質量。考慮液相介質以簡單的周期形式脈動。結合Euler-Bernoulli梁模型構建橫向振動數學模型。采用Galerkin方法將方程離散,并將各參數進行歸一化處理。通過求解方程線性部分獲得管道固有頻率及臨界氣速隨表觀氣速、表觀液速的變化規律。采用四階Runge-Kutta法對方程進行迭代求解。采用包括位移幅值,位移-速度相圖以及位移的功率密度譜(power spectral density,PSD)等手段來研究管道系統非線性振動特性。

1 環狀流水平輸流管道橫向振動模型

兩端簡支環狀流輸流管道系統,如圖1所示。氣、液相分別以表觀流速uSG和uSL從入口流入并在管道內形成環狀流從出口流出。系統由長度為L,截面積為Ai,抗彎強度為EI的水平直管及兩端簡單支撐構成。

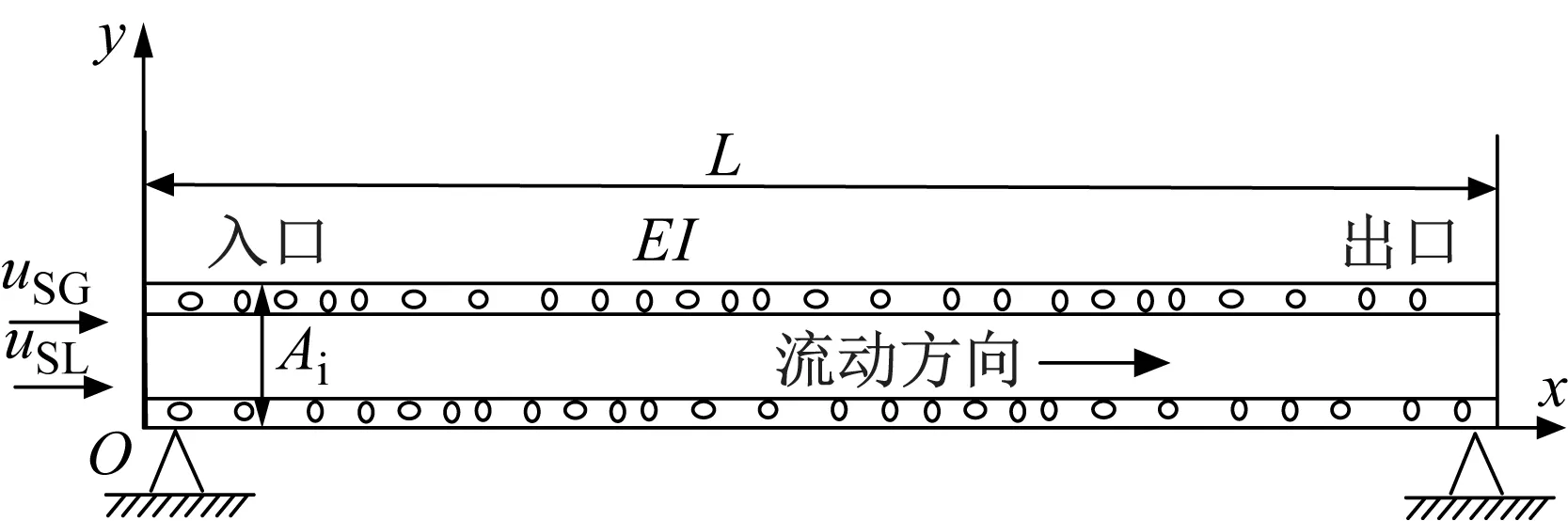
圖1 輸送環狀流兩端簡支管道系統示意圖

研究基于以下假設：①管道不計剪切力的影響采用Euler-Bernoulli梁模型描述;②忽略外部阻尼的影響;③管道材料為黏彈性,且符合Kelvin-Voigt假定。

對于兩端簡支的水平管道系統,管道在振動過程中因彎曲變形而伸長產生附加軸力。此外,根據Pa?doussis[20]忽略重力效應影響。基于Dai等[21]和Monette等[22]的研究結果,考慮軸向附加力忽略重力效應的影響時,輸送氣-液兩相環狀流的運動方程可以寫為

(1)

uSL=HLFuL

(2)

uSG=(1-HLF)uG

(3)

式中：HLF為液膜持液率;uL,uG為氣、液相真實流速,因此單位長度氣、液質量mL=ρLAiHLF,mG=ρGAi(1-HLF)。基于氣芯與液膜動量平衡

(ρL-ρG)gsin(θ)=0

(4)

式中：τF,τI分別為液-壁與氣-液間的剪切力;SF,SI分別為相應剪切力作用下的濕周。分別由下式計算

SF=πdΘ

(5)

(6)

(7)

其中,

(8)

SCD=dsin(πΘ)

(9)

(10)

(11)

(12)

利用式(2)～式(12)便可以獲得流動參數,具體求解過程詳見Zhang等[23]的研究。

引入如下變量和參數將式(1)進行歸一化處理

從中可以看出,vg,vl與各自的單位長度質量和管道長度有關。由于氣、液兩相介質的密度差較大,因此,即使二者的速度相差很大,但歸一化后二者將相差很小。

將各分量無量綱參數代入式(1)整理

(13)

vl=u0[1+μcos(ωτ)]

(14)

式中：μ為脈動幅值;ω為脈動頻率。

將脈動的液相流速代入式(13),并將脈動項和非線性項移到方程右側

(15)

采用Galerkin離散方法將式(15)高階偏微分方程離散化為低階常微分方程,橫向位移用式(16)表示

(16)

式中：qj(τ)為廣義坐標;N為階數,本文考慮振動前兩階振動情況因此N取2;Q=[q1(τ),q2(τ),…,qN(τ)];Φ=[φ1(ξ),φ2(ξ),…,φN(ξ)];φi(ξ)為振型函數,這里采用對應于梁模型的振型函數代替,對于兩端簡支管道

(17)

將式(16)代入式(15),左乘ΦT并對ξ在[0,1]進行積分,得

(18)

其中,

其中,

B=[0,-b;b,0],D=[d11,0;0,d22],

(19)

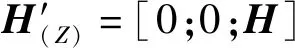
(20)

管道系統的固有頻率用系數矩陣S的特征根表示

(21)

特征根Γ的虛部ω1和ω2為對應于管道系統的一階和二階固有頻率,特征根Γ的實部r1和r2為對應于系統一階和二階模態的能量。管道系統的非線性振動特性采用四階Runge-Kutta法進行求解。

2 結果與討論

2.1 模型驗證

模型分析過程中參數選擇為：管道內徑Di為0.025 m,外徑Dout為0.032 m;管道的彈性模型E為4.35 GPa;管道密度ρp為1 180 kg/m3。兩相介質采用水、空氣,其密度ρL,ρG為998 kg/m3,1.209 kg/m3;氣、液表觀速度分別選取為uSL=0.1～0.9 m/s,uSG=20～40 m/s。根據文獻[24]此速度范圍處于環狀流。由于缺少關于環狀流管道振動位移的相關研究,采用本文方法計算獲得的固有頻率與劉剛等的計算結果進行對比用以驗證本模型,如圖2所示。值得注意的是,實部和虛部分別代表管道振動能量和頻率,從圖2可以看出二者吻合的很好。

(a) 一、二階固有頻率虛部

2.2 固有頻率與臨界氣速

本節主要研究了管道固有頻率與臨界氣速隨表觀氣速與表觀液速的變化規律。圖3為管道一階固有頻率實部與虛部隨表觀氣速與表觀液速變化情況。從圖3(a)中可以看出對應于每個表觀液速下的管道固有頻率隨著表觀氣速增加而降低。當固定表觀氣速時,固有頻率隨著表觀液速增加而降低。也就是說無論增加液速還是增加氣速均會導致管道固有頻率的降低。值得注意的是,表觀液速對固有頻率的影響更為顯著。此外,當uSL≥0.5 m/s時存在臨界氣速,且臨界氣速ucr隨著表觀液速增加而降低。這也再次說明表觀液速的增加對系統的穩定性是不利的。需要指出的是,這并不意味著臨界氣速只存在于uSL≥0.5 m/s系統,隨著管道長度或表觀氣速的增加,臨界氣速也會發生在uSL<0.5 m/s的管道系統中。

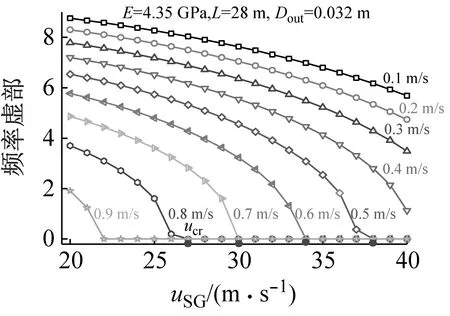
(a) 一階固有頻率虛部隨表觀氣、液速度變化圖

從圖3(c)中可以看出,當uSL=0.1 m/s時,固有頻率隨表觀氣速增加降低的幅度較為平緩,最大降幅為0.251 3。固有頻率降低幅度隨著表觀液速增加而顯著增加。

在環狀流動狀態下,管道內氣、液兩相的速度相差很大,然而二者速度歸一化后相差很小,如表1所示。這主要是由于氣、液兩相介質的密度差造成的。在固定表觀液速條件下,增加表觀氣速導致相間剪切力增加,因此使得液膜厚度降低,氣芯面積增加,這也將導致單位長度液體質量降低,單位長度氣體質量增加。因此,氣、液兩相介質對管道固有頻率及臨界氣速的影響主要取決于液相介質的液膜厚度(單位長度液相質量)。

表1 歸一化速度與單位長度質量

2.3 非線性振動特性

圖4為在uSG=40 m/s,μ=0,ω=0條件下,以管道長度為控制參數的分岔圖。從圖4可以看出表觀液速從0.9 m/s減小到0.2 m/s過程中,對應管道分岔起點由21.8 m增加到31.9 m。這意味著在低表觀液速條件下管道更穩定。此外,隨著表觀液速增加位移幅值增大。值得注意的是在不考慮速度脈動時所呈現的分岔為Pitchfork分岔。

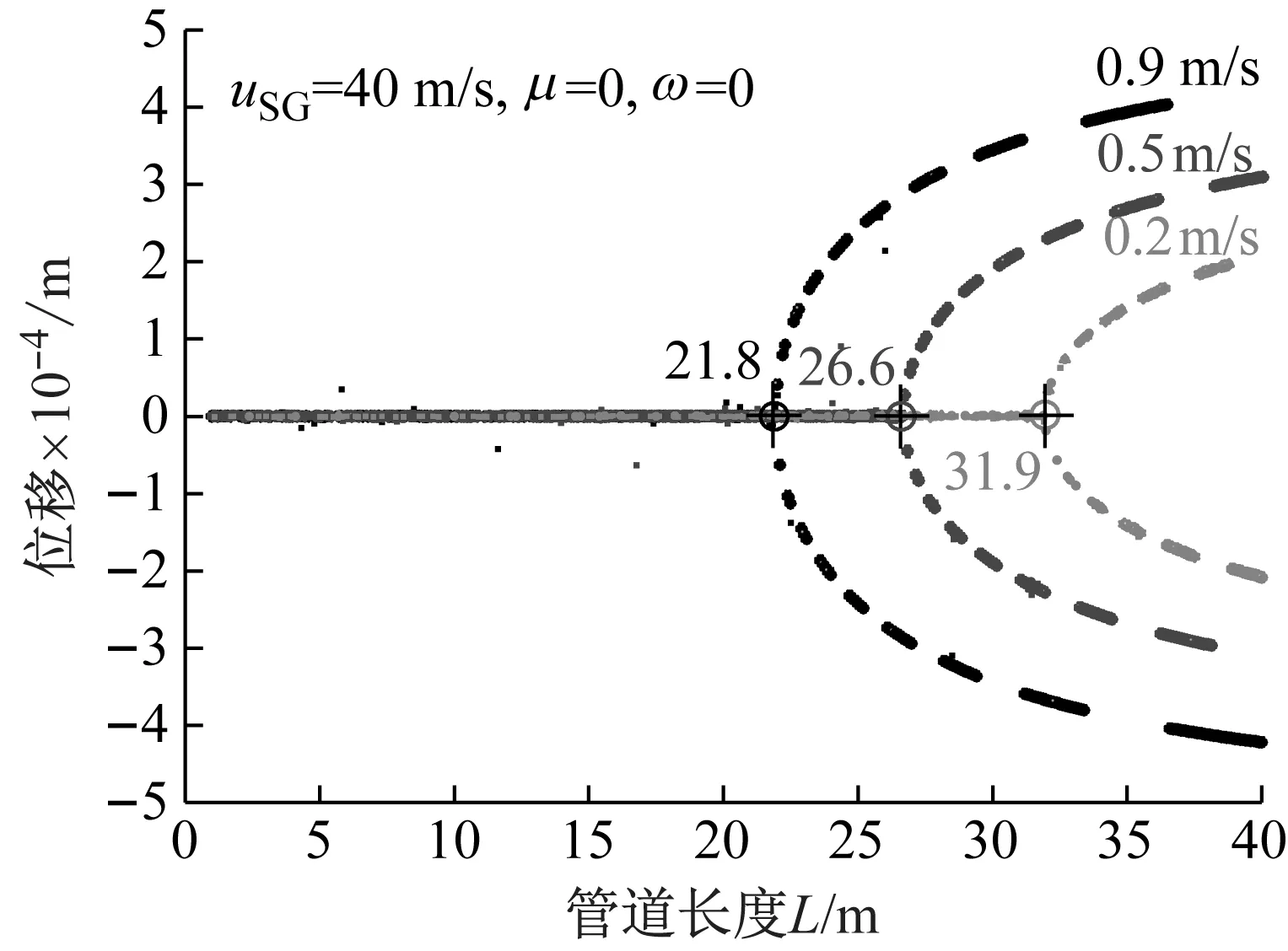
圖4 不同液速條件下以管道長度L為控制參數的分岔圖

圖5為在uSL=0.9 m/s,uSG=40 m/s,ω=25,μ=0.4條件下,以管道長度為控制參數的分岔圖。從圖5可以看出,在管道長度為18.3 m處出現了分岔,隨著管道長度進一步增加,系統經過多次分岔后最終達到了混沌狀態。這意味著液相介質的脈動使得系統更加不穩定,而且這種不穩定將導致系統出現混沌。

圖5 ω=25,μ=0.4,uSL=0.9 m/s,uSG=40 m/s條件下以管道長度L為控制參數的分岔圖

對比圖4、圖5可以發現當考慮液相速度的脈動時,系統的分岔起始位置不僅由21.8 m降低至18.3 m而且還會使得系統的振動變得混沌。因此,有必要進一步研究激勵頻率對管道振動特性的影響。圖6為以激勵頻率ω為控制參數的分岔圖。基本參數如下：uSL=0.9 m/s,uSG=40 m/s,L=40 m,μ=0.4,ω=0～70。從圖6可以看出隨著ω變化管道振動狀態發生了數次突變。然而,從分岔圖中無法具體分辨出分岔路徑和振動形態。

圖6 以ω為控制參數的分岔圖

為了能夠清楚的展示系統振動形態的轉換過程,借助相軌跡圖、PSD以及龐加萊截面方法來研究激勵頻率ω=35～42變化過程中系統振動形態的變化。當ω=35時(見圖7(a)),系統顯示出非常混亂的軌跡線,這些軌跡線看似非常混亂但又不缺乏一定的自相似特性。從其PSD圖中可以看出曲線具有寬頻特性,而且龐加萊截面圖顯示出雜亂的點,這表明系統處于混沌狀態。當ω=38.1時(見圖7(b)),從其PSD圖中可發現其并不具備寬頻性質,只顯示出一些譜尖點出現了概周期的性質,其龐加萊截面圖上的點呈現一條線,說明系統處于概周期運動。當ω進一步增加至42時,系統出現倍周期和周期運動的振動形態。綜上,液相流速的脈動將會導致管道系統出現包括混沌、概周期、倍周期的非線性振動形態,這與所選擇的激勵頻率值有關。

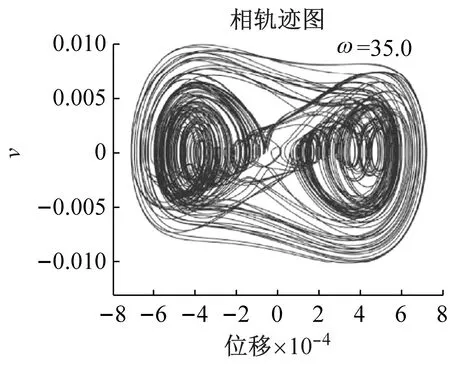
(a) ω=35.0系統相圖、PSD圖以及Poincare圖

此外,混沌對初值非常敏感。圖8為不同初始條件下管道中心位移混沌響應。從圖8(a)中可以看出當初始條件初始位移大小相等僅改變初始振動方向時,管道中心振動位移的時間響應曲線卻又很大的變化,出現了大小相等但振動方向相反的現象。當初始位移方向相同僅有很小的改變由-0.001改變為-0.002,管道中心振動位移的時間響應曲線也出現了很大的不同(如圖8(b)),隨著時間的變化并沒有出現振動的一致性。說明在這種條件下振動對初始條件極其敏感。

3 結 論

本文對氣液兩相環狀流水平輸流管道非線性振動特性進行了分析,方程采用Galerkin法進行離散。研究了固有頻率、臨界氣速、混沌與分岔等基本動力學特征并得到如下結論：

(1) 表觀液速對系統線性不穩定性影響較大,在L=28 m,uSG在20～40 m/s條件下,固有頻率隨著表觀液速的增加而降低。當uSL≥0.5 m/s時系統存在臨界氣速且其隨著表觀液速的增加而降低。

(2) 不考慮脈動時管道系統出現Pitchfork分岔,表觀液速由0.2 m/s增加到0.9 m/s過程中分岔起點由31.9 m降低到21.8 m,說明隨著表觀液速的增加,管道的穩定性降低。

(3) 當液相介質脈動時,分岔起始點降低至18.3 m,且隨著長度增加分岔次數加倍直至出現混沌。此外,隨著激勵頻率的增加,系統存在多種振動形態包括多種形式的周期運動、概周期運動同時也有混沌運動的可能。這種混沌狀態對初值十分敏感。

綜上所述,液相速度的大小及脈動特性對管道振動特性影響十分顯著,該研究對工程應用具有一定的指導意義。