復雜載荷下動態拉桿力測試方法研究

李盼菲，周琦，劉勇，謝雙林

（鄭州機電工程研究所，河南鄭州，450015）

0 引言

拉桿用于支撐重機械的大梁或者前臂，其作用十分重要，拉桿的強度以及安全系數是設備安全性能的重要保障。由于拉桿的強度不足而導致的斷裂事故屢見不鮮，因此拉桿的安全系數已經成為重機械安全性能的首要指標。研究拉桿強度的計算方法和測試技術，從理論和實踐兩方面同時著手來對拉桿強度進行研究，具有十分重要的意義[1]。通過應力應變測試以及力的動態測試結果，可以在一定程度上判斷矢穩的大致位置和狀態，從而有針對性的進行結構優化設計，來達到提高強度的目的[2]。目前，工程應用上使用壓力傳感器、多向或單向應變片等來進行應力測量，但是，應力應變的測量通常是在施工現場進行的，拉桿的受力并不是規則和均勻的，其同時受到多種復雜的載荷耦合作用，導致測試十分困難。因此，我們要得到高質量的數據，達到較高的測試準確度，同時能夠避開這些復雜載荷帶來的測試難度大的問題，需要對測試方法進行進一步的探索和研究。

本試驗工況中，某系統使用拉桿進行復雜作用力的傳遞，期間拉桿隨著結構動作上下運動，且運動不在一條直線上，拉桿上承受拉力和壓力不規則交替循環。為了測量此拉桿軸向受力情況和彈性變形，判斷其是否屈服，需要對其同時進行軸向拉壓力和應變測量。由于工作狀態的安裝空間限制，測量傳感器不能安裝在桿兩端，且重量不能太大，以免干擾拉桿受力情況，因此普通的力傳感器不能夠滿足此試驗測試要求。張紅星[3]使用應變計埋填法，將應變片埋入螺栓孔中，通過粘合劑進行應變的傳遞，有效地解決了復雜工況下傳感器安裝困難的問題；桂永旺等[4]在同一錨桿上使用多種方法測試，指出在復雜受力時應采用多面粘貼應變計的方法進行測試；蘇橋等[5]通過電阻應變計和力傳感器兩種方法對轉向橫拉桿的受力情況進行測試，來計算最大齒條力，并得出結論，此兩種方法用于測力均比較合理。在動態測量環境中，鄭韜等[6]的試驗證明，應變式力傳感器對于高速拉伸載荷震蕩有明顯改善，因此，本試驗使用應變片構造惠斯通電橋來測試拉桿受力情況。

1 測量原理

本試驗拉桿是一個一次超靜定結構，需要找出變形協調條件，其變形協調條件又不同于一般的固定支座，而是一個拉桿的彈性變形支座位移，并且在安裝之后是傾斜的，并不垂直，所以需要先將傾斜力分解，這種不與受力桿件垂直的超靜定結構的支座位移并不為零，也就是變形協調條件的變形綜合并不為0，因此其不是一般意義的一次超靜定結構的力法正則方程。而我們的計算采用解除拉桿約束，代之以力表示，后拉桿的彈性變形量也就是后拉點支座變形的總和[7]。根據本試驗件的力學模型，除了自重載荷外，其余的外載荷并非同時作用在拉桿上，也就是說，其作用的位置和作用的方向、時間也有一定的偏差，那么我們計算的時候，分別計算其載荷情況進行線性疊加即可。另外，由于傾斜的拉桿力對其形心產生的附加彎矩不可忽略，我們曾經比較過考慮此彎矩和忽略此彎矩的計算結果，發現差別比較大，所以計算時，雖然比較麻煩，但是我們依然將其考慮在內[8]。在正式試驗加載復雜載荷的時候，我們通過貼在拉桿表面的應變片來將軸向應變記錄下來，并轉化為電阻變化量，利用采集裝備再將其轉化為電壓的變化量，通過信號的調理和放大來進行采集處理，能夠最大程度的提高信噪比，獲取有用信號。

應變表達式為：

式中：ε 為微應變，Δl 為彈性形變量，l 為桿總長。

在實際測量中，應變量是極其微小的，由應變引起的電阻的變化量也是非常小的，但是電壓的變化卻較為明顯。在工作過程中，拉桿受到拉壓力時，其表面的軸向應該是單向應力，但是橫向也存在應變，其應變量與軸向應變量有一定的關系，我們把它們之間的比例成為泊松比，用μ 來表示。這個橫向應變并不是我們想要測量的，因此，我們需要采取一定的方式將其抵消掉。一般情況下，構建惠斯通電橋，將其橫向應變的兩個橋臂作為相對橋臂可以抵消。如圖1 所示。

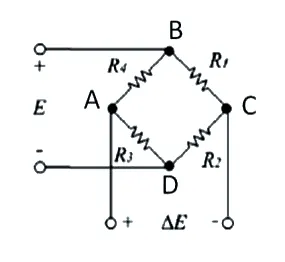
圖1 惠斯通電橋

圖1 中，四個橋臂電阻分別為R1、R2、R3、R4，我們在BD 兩端給全橋電路供電，供電激勵電壓為E，同時在AC 兩端測量全橋電路的輸出電壓ΔE。本試驗應變片采用T 型貼法，相對橋臂的兩個應變片R1、R3 敏感柵與拉力方向平行，即軸向，R2和R4 的敏感柵方向與拉力方向垂直，可以消除偏載誤差和溫度帶來的誤差[9～11]，如圖2 所示。

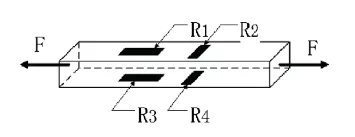
圖2 應變片粘貼示意圖

圖2 中，R1、R3 應變片的敏感方向為軸向，主要用來測量拉桿的軸向應變，是本實驗中的工作應變 片。R2、R4 的 敏感方向為橫向，與軸向垂直，主要用來補償和抵消橫向應變產生的影響，因此，其為補償應變。圖中F 表示拉桿的軸向受力。其軸向受力是復雜的、動態的多種載荷疊加的結果。在試驗中，由軸向作用力F 產生的應變片R1、R3 的應變量為εF，同時考慮到應變片受到溫度變化而產生的感應應變量εt，則各個橋臂產生的應變量為：

式中：μ 為拉桿材料的泊松比。

圖1 中，在BD 處加激勵電壓E，AC 點輸出電橋電壓ΔE。電阻R1、R2、R3、R4 為橋臂電阻，則電橋輸出電壓表達式為：

本試驗中使用四個相同應變片搭建電橋，應變片型號為KFGS-1-120-D17-11L1M2S，應變公式為式(5)。其應變電阻均為120Ω，即R1=R2=R3=R4。應變系數相同，均為2.06，即式(5)中，四個橋臂的K 值相等。

將式(2)(3)(5)帶入式(4)中，可得：

通過輸出電壓ΔE 的變化可以得到軸向作用力F 產生的應變為：

在拉桿的屈服強度內，軸向應變量εF與軸向拉力F 成正比關系，根據式(7)可知，拉桿所承受的拉力與電橋輸出ΔE 成正比關系，即：

因此需要對測量系統進行標定得到式(8)中K 與b 值，即可通過橋路輸出電壓測量拉桿所承受的軸向拉力。

2 系統標定

對前面構建的系統進行標定，首先，根據圖中示意將軸向應變片和橫向應變片粘貼在拉桿表面，將應變片的線路按照電路圖構建全橋電路，在材料機上對拉桿進行標定。我們規定當拉桿受到壓縮力時，輸出為負，收到拉伸力時，輸出為正。

在BD 兩端加載電橋電壓E 為2.5V，在AC 兩端測量橋路輸出。將拉桿豎直掛起，標定之前，已經有重力等作用力加載到拉桿上，此時電橋已經有電壓輸出。在加力之前，將測量系統進行清零處理，即設定b 值為0。因為試驗時并沒有初始拉力，但采集系統仍具有微小的電壓輸出，此電壓受到環境溫度影響并不固定，需要在實驗前進行清零操作，即設定b 值為0。

在拉桿上加載拉力，穩定之后記錄電橋的輸出，通過最小二乘擬合算法，算出K 值。得到測量數據與施加力的關系曲線如圖3 所示。

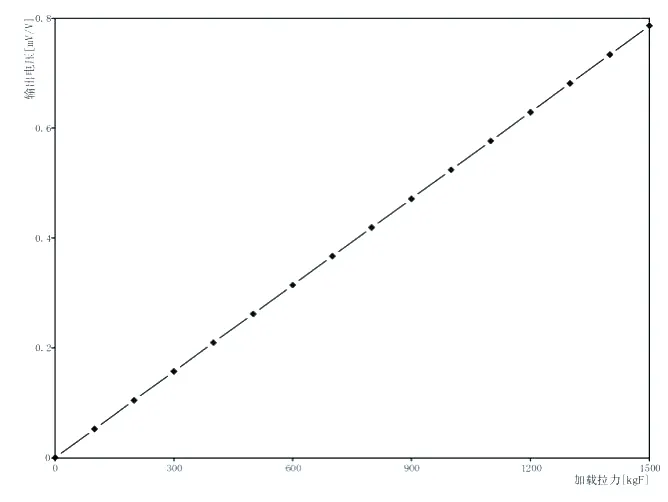
圖3 標定數據

根據最小二乘擬合算法，得到k 值為1907.145kgF/mV/V。將標定后的拉桿安裝在試驗樣機上，檢查其他參數設置，使之滿足試驗要求。

3 試驗數據分析

為了測試電橋測量方法的穩定性和可靠性，試驗時同時在拉桿上測量應變。測量設備使用DEWETRON 公司的DEWE-50-PCI，搭載STG 程控模塊進行測試，測量精度高達0.05%。試驗進行四次，每次試驗開始時對設備進行電壓清零操作，即不保留初值。數據如圖4 所示。圖中曲線S1 為應變曲線，單位為微應變（με），F 為通過惠斯通電橋測出的拉力曲線，單位為公斤力（kgF）。

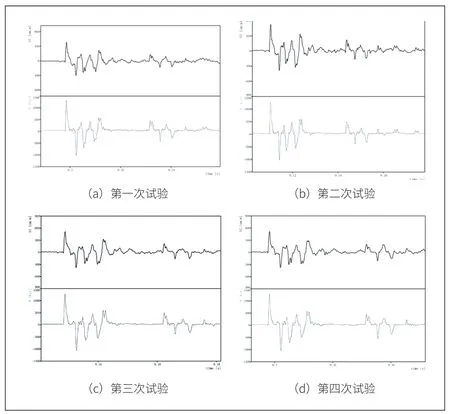
圖4 試驗測試數據

從上述試驗結果可以看出，四次的機構動作基本相同，先是機構拉伸動作，緊接著開始壓縮，在拉伸受力和壓縮受力之間震蕩幾次后恢復原狀。在此過程中，由于拉力與應力的測量手段相同，因此其頻率響應基本相同，從圖中可以看出，測量頻率范圍能夠滿足機構動作測量需求。四組試驗數據中，應變曲線與拉力曲線的幅值基本一致，證明本試驗通過應變片組成惠斯通電橋測力的方案可行[12]，同時，也驗證了文中式(7)與式(8)的理論正確性。試驗中，綜合采集設備、標定設備、應變片粘貼誤差等，計算出其擴展不確定度為2.24%（k=2）。四次重復試驗，曲線一致性良好，且與本結構件的試驗狀況和預示值基本吻合，證明本次測試數據可信度高，本方案用于工程測試中比較可靠。但是本實驗方法也有一定的不足之處，在測量時將拉桿等效為二力桿，而在實際試驗中，結構發生平面外變形時，撐桿是彎曲的，應該等效成梁進行計算。

4 結語

由于計算系數時的擬合算法比較復雜，文章省去了其推導和計算的過程，直接給出了計算結果。即便如此，計算和測量過程依然十分復雜。本文利用了先進的設備和計算軟件，最終計算出了在實戰狀態下的應力應變值和拉桿動態受力值，即為各工作狀態下的拉桿力大小，由此來驗算拉桿的屈服狀況。

由以上分析可以知道，本文所采取的使用應變片直接粘貼于結構件表面組成惠斯通電橋測量拉壓力的方法，具有很強的可操作性，不會改變拉桿的原始結構及受力狀態，并且測量結果精準可靠，能夠滿足工程應用，對于結構件的后續安裝和使用提供了強有力的數據支撐。

本試驗方法試驗成本低，安裝簡單，數據可靠性高，測試結果合理，拉壓力的測量與拉桿的應變變化規律基本一致，并且有效避開了拉壓力傳感器安裝困難的問題，在大多數復雜載荷、復雜環境的拉壓力測試環境中具有極大的優勢。