考慮功率平滑的混合儲能系統容量優化方法研究

王 偉 程 辰 宋光明 祁 鳴

（國網安徽省電力有限公司合肥供電公司，安徽 合肥 230022）

0 引言

隨著微電網中風力發電、光伏發電等波動性電源的比例與日俱增，其輸出功率的隨機性與波動也越來越大，給電網運行帶來了沖擊[1]。儲能系統具備雙向出力、響應速度快、運行靈活等優點，給微電網波動問題帶來了新的解決途徑。其中混合儲能技術能夠整合各種儲能裝置的優點，可應用于微電網的功率平滑[2]。

合理選取儲能容量是保障微電網經濟運行的前提，本文首先建立了包含鋰電池與超級電容的混合儲能等效模型，在此基礎上以成本最低為目標，采用遺傳算法求解滿足功率波動約束的混合儲能系統最優配置。考慮到功率波動的隨機性，引入柔性約束，分析了允許儲能系統實際輸出與目標輸出之間存在一定偏差時對其容量的影響，為混合儲能系統配置時性能與成本的折中提供參考。

1 混合儲能等效模型

儲能系統能夠協助微電網參與功率平滑，增強系統穩定性，但單一的儲能裝置存在局限性[3]，因此本文采用混合儲能系統，結合鋰電池與超級電容，整合兩種儲能裝置的優勢，協助微電網實現功率平滑。

1.1 鋰電池等效模型

為簡化混合儲能模型，采用等效電路模型對鋰電池的動態特性進行分析，如圖1所示。

其具體動態特性如下：

式中：Pb為鋰電池輸出功率；Uob為鋰電池開路電壓，一般為定值。

則鋰電池的荷電狀態可由下式得出：

式中：Qb為鋰電池額定容量。

1.2 超級電容等效模型

采用等效電路模型對超級電容的動態特性進行分析，如圖2所示。

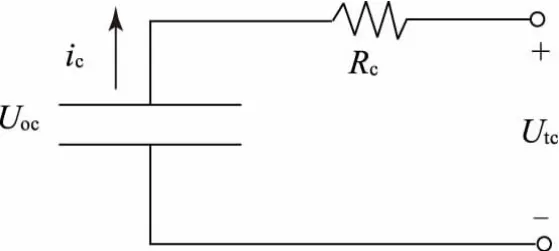
圖2 超級電容等效電路

其具體動態特性如下：

式中：Puc為超級電容輸出功率。

則超級電容的荷電狀態可由下式得出：

式中：Qc為超級電容額定容量。

由于超級電容開路電壓會隨SOC變化，所以開路電壓Uoc可由下式得出：

式中：Umax為超級電容滿電量時的電壓。

綜上所述，本文建立了鋰電池與超級電容的電流、電壓、輸出功率等包含儲能動態特性數據的等效模型。將上述鋰電池與超級電容模型相結合即可得到混合儲能模型，其中鋰電池與超級電容在充放電特性上各有優劣，在對包含混合儲能系統的微電網進行功率平滑時，可以分析兩者動態特性，根據所需平滑功率對鋰電池與超級電容承擔的功率進行合理分配，充分利用兩種儲能裝置優勢，提升功率平滑的精度與速度。

2 混合儲能容量優化

2.1 優化目標和約束

儲能系統的容量越大，平滑的效果越理想，但相應的投資成本也會隨之增加。以最小的成本投入獲得最優的性能，即實現儲能系統的最高性價比是普遍追求的目標。在性能目標上，要求平滑后整個系統的聯合輸出功率在最大程度上滿足設定的波動率約束；從經濟性的角度，要求整個儲能系統的投資成本最小。

如此來說，微電網中混合儲能系統容量優化目標可描述為：

目標函數一：混合儲能系統的投資成本Ctotal，HES最小。

式中：Ctotal，HES表示混合儲能系統總投資成本；CP，SC、CP，B分別表示單位功率的超級電容和鋰電池的成本；CE，SC、CE，B分別表示單位容量的超級電容和鋰電池的成本；PSCN、ESCN分別表示超級電容的額定功率與額定容量；PBN、EBN分別表示鋰電池的額定功率與額定容量。

目標函數二：使平滑后目標外電量百分比最小。

式中：RE，abd表示系統輸出目標外電量百分比；Ptarget表示系統聯合目標輸出功率；PG表示電網中可再生能源輸出功率；PHES表示t時刻混合儲能系統實際的聯合輸出功率，即：

式中：PSC（t）、PB（t）分別表示超級電容和鋰電池t時刻的實際輸出功率，超級電容與鋰電池是各自獨立管理的。

對于上述多目標優化問題，本文采用目標函數一作為混合儲能系統容量優化的綜合目標函數，而將目標函數二通過罰函數轉化為相應的約束條件，轉化后的模型可用式（9）和式（10）表達。

目標函數：混合儲能系統的總投資成本最小。

約束條件：

式中：RE，abd表示目標外電量百分比；RE，abd_permit表示平滑后目標外電量百分比的最大允許值；SOCSC，max與SOCSC，min分別表示超級電容荷電狀態允許的上、下限；SOCB，max與SOCB，min分別表示鋰電池荷電狀態允許的上、下限。

2.2 優化問題的求解

針對式（9）、式（10）構成的優化問題，約束條件中平滑后目標外電量百分比不超過最大允許值為柔性約束條件，即在一定的概率下允許混合儲能系統的輸出功率與給定目標值之間存在偏差。針對這類優化問題的求解，遺傳算法具有較好的適應性[4]。求解主要包括以下幾個步驟：

1）初始化種群，輸入種群中的個體數、交叉率、變異率及迭代次數，通過隨機化方法產生初始種群，種群中每個個體攜帶的染色體包含了混合儲能系統中各儲能介質的額定功率與容量。

2）功率分配，對混合儲能系統中超級電容與鋰電池的輸出功率進行分配，獲得功率型儲能介質和能量型儲能介質的荷電狀態、最大充放電功率以及混合儲能系統的總出力。

3）計算適應度函數值，計算每個個體所代表的混合儲能系統的額定功率和容量所對應的總投資成本，以此為基礎計算每個個體所攜帶的染色體的適應度函數值。滿足約束條件的染色體適應度函數值高，不滿足約束條件的染色體適應度函數值低。

4）選擇，選取種群中適應度函數值較高的染色體直接遺傳給下一代，適應度函數值較低的染色體被淘汰。

5）交叉與變異，按照設定的交叉率和變異率，將交叉算子和變異算子作用于種群，獲得經過交叉與變異的新一代染色體，遺傳給下一代。

6）循環迭代，檢驗是否達到設定的迭代次數，是則進入步驟7），否則重復步驟2）至步驟5）。

7）給出最優解，選取計算尋優過程中適應度函數值最高的染色體所對應的混合儲能系統各儲能介質的額定功率與容量作為最優配置方案。

3 算例分析

采用由超級電容和鋰電池組成的混合儲能系統平滑可再生能源輸出功率的波動。超級電容和鋰電池的仿真參數如表1所示[5]。

表1 超級電容和鋰電池的仿真參數

表2 混合儲能系統容量優化結果

采用本文所述的混合儲能系統容量優化方法，運用遺傳算法求解混合儲能系統最優配置容量。種群個體數目為50，遺傳進化過程中種群規模維持不變，最大進化代數取為50代，交叉率為0.7，變異率為0.01。計算得到超級電容和鋰電池的容量及功率如表2所示。

若允許混合儲能系統平滑后的系統實際輸出功率與給定的目標輸出之間存在偏差，即RE，abd不為零，圖3給出了目標外電量百分比RE，abd=5%時平滑后的輸出功率。

圖3 目標外電量百分比RE，abd=5%時平滑后的輸出功率

允許目標外電量存在，對混合儲能系統額定功率和容量的要求也會相應發生變化，不同目標外電量百分比對應的混合儲能優化配置結果如圖4所示。

圖4 儲能優化配置結果隨目標外電量百分比的變化情況

從圖4可以發現，隨著目標外電量百分比的增加，鋰電池的額定功率和容量單調下降；超級電容的額定功率先緩慢增加，在RE，abd為5%～10%時達到最大，然后迅速下降，超級電容的額定容量也隨之呈現先上升后下降的趨勢。由此可見，目標外電量百分比允許值低于10%時，超級電容逐漸占據主導地位，而鋰電池的作用越來越弱。

綜合比較可知，混合儲能系統的額定功率隨著目標外電量百分比的增加而減少，例如，RE，abd從0增加到5%時，混合儲能系統的額定功率下降27.4%；RE，abd為10%時，降幅接近50%。混合儲能系統的額定容量也隨之減少，但下降速度相對較慢。

4 結論

本文建立了包含鋰電池與超級電容的混合儲能等效模型，以混合儲能系統的總成本最低為目標，運用遺傳算法求解混合儲能系統的最優配置。通過仿真驗證，得到如下結論：采用遺傳算法求解包含柔性約束的優化問題能夠收斂至最優解，適當放寬對平滑目標的要求能夠大幅減少混合儲能系統的功率與容量，這可以為混合儲能系統配置時性能與成本的折中提供參考。