技術搭臺覓本質，深度探究現通法

崔豪東　方處云

［摘? 要］ 信息技術與深度探究的融合發展，不是讓信息技術來刺激眼球，而是在必要的時刻來推波助瀾，讓學生去深度探究知識本質，發現解題通法，進行高效的課堂學習.

［關鍵詞］ 信息技術；深度探究；GeoGebra軟件；動點路徑；圖形變換

《教育信息化2.0行動計劃》指出：“應將教育信息化作為教育系統性變革的內生變量，支撐引領教育現代化發展，推動教育理念更新、模式變革、體系重構. ”信息技術下的數學課堂既要達成教學模式變革的新時代要求，又要讓課堂成為培育學生實踐與創新的搖籃. 今年，筆者有幸開設了以“技術支持下的初中數學創新課堂教學”為主題的市級公開課“動點路徑與圖形變換”. 下面筆者呈現本節課的教學背景和教學過程，并結合本節課談談對信息技術與深度探究融合發展的一些思考.

教學背景

動點路徑問題是一類抽象程度較高、思維深度較大的數學問題，它是九年級常考的一類問題. 依托粉筆黑板，以傳統的講授法去教學，學生無法直觀感受動點的變化，教師很難講清，學生很難理清，課堂沉悶無趣. 借助信息技術，以簡單的演示法去教學，學生雖能直觀觀察到動點的運動，但由于視覺直接，未經思維推理，難以顯現通法. 因此，筆者在“信息技術何時亮相，深度探究如何開展”上進行了深入思考，以期促進信息技術與深度探究高效融合發展，經過三次磨課、三次修改，本節課得以成型. 適時引入信息技術手段，助力學生深度探究，思考此類問題的本質，彰顯解決問題的通法，這是本節課的全新探索和大膽嘗試.

教學過程

1. 探究激發猜想，技術展露風采

問題1? 如圖1所示，點P在線段MN上運動，A是MN外一定點，△PAQ是等腰直角三角形，∠PAQ=90°，AP=AQ，試探究點Q的運動路徑.

師生活動1：教師呈現問題1，給足時間讓學生思考. 學生思考后分享自己的想法.

生1：如圖2所示，我先讓點P與點M重合，找到點Q所在的位置M′，再讓點P與點N重合，找到點Q所在的位置N′. 連接M′N′，我發現點Q就在線段M′N′上運動.

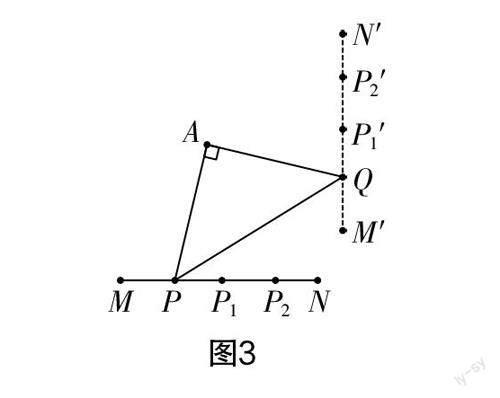
生2：如圖3所示，我和生1一樣，先找到了點M′和點N′. 接著我在線段MN上取兩點P和P，然后讓點P分別與P，P重合，找到點Q所在的位置P′，P′，我發現點P′，P′也在線段M′N′上.

生3：可以盡可能多地在線段MN上取點P，P，P，…，然后讓點P分別與P，P，P，…重合，找到點Q所在的位置P′，P′，P′，…，點P′，P′，P′，…應該都在線段M′N′上.

師生活動2：教師引導學生利用平板上的GeoGebra軟件作圖驗證，并利用平板的屏幕巡視功能及時查看學生的作圖情況，當學生遇到作圖難點時適時介入.

生4：作好線段MN和點A后，我在線段MN上任取一點P，連接線段AP，接著如何作出點Q呢？

師：點P和點Q有什么變換關系嗎？

生5：點Q可看作點P繞點A逆時針旋轉90°得到的. 首先點擊“變換—旋轉”的命令，接著依次選中點P（旋轉對象）和點A（旋轉中心），然后輸入90°（旋轉角度），即可得到點Q.

生6：如圖4所示，我在線段MN上取點P，P，P，P，P，然后讓點P分別與P，P，P，P，P重合，借助GeoGebra軟件的旋轉變換功能，找到點Q所在的位置P′，P′，P′，P′，P′. 經驗證，點P′，P′，P′，P′，P′都在線段M′N′上.

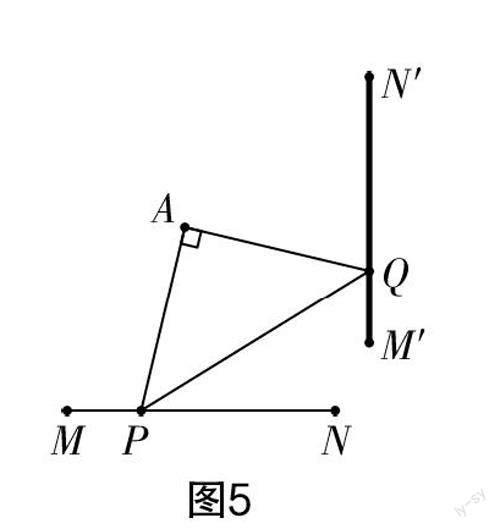
生7：如圖5所示，借助GeoGebra軟件的顯示軌跡功能，我拖動點P使其在線段MN上運動起來，點Q的運動路徑就形成了. 可以看到，點Q的運動路徑是線段M′N′.

生8：生7借助技術，使點P取遍了線段MN上的每一個點，找到了點Q走過的每一個位置. 完美地驗證了點Q的運動路徑是線段M′N′.

師生活動3：小組成員相互合作，完成作圖的學生去指導未完成作圖的學生，確保每一位學生都經歷取點個數“由少到多”的作圖過程，成功驗證點Q的運動路徑是線段M′N′.

生9：如圖6所示，我和組內同學借助GeoGebra軟件的旋轉變換功能，把線段MN（點P的運動路徑）繞點A逆時針旋轉90°得到線段M′N′，就把線段MN上的每一個點P經旋轉變換后的對應點Q全部找到了，可以發現點Q的運動路徑是線段M′N′.

生10：在顯示動點路徑時，我發現點Q是由點P繞點A逆時針旋轉90°得到的，所以點P的運動路徑MN繞點A逆時針旋轉90°就能得到點Q的運動路徑M′N′.

生11：這道動點路徑問題與圖形的旋轉變換有關系，即只需知道動點P與動點Q之間的旋轉變換關系，就可確定點P的運動路徑與點Q的運動路徑之間的旋轉變換關系，因此把點P的運動路徑進行對應的旋轉變換即可得到點Q的運動路徑.

生12：旋轉不改變圖形的形狀和大小. 點P的運動路徑是線段，點Q的運動路徑也是線段（形狀相同），而且點P與點Q的運動路徑的長度相等（大小相同）.

2. 觸類何以旁通，再借技術探秘

問題2? 如圖7所示，點P在線段MN上運動，A是MN外一定點，Q為AP上一點，AQ=AP，試探究點Q的運動路徑.

師生活動4：教師呈現問題2，給足時間讓學生思考. 學生思考后分享自己的想法.

生13：如圖8所示，我先讓點P與點M重合，找到點Q所在的位置M′，再讓點P與點N重合，找到點Q所在的位置N′. 連接M′N′，我發現點Q在線段M′N′上運動.

生14：如圖9所示，我和生13一樣，先找到了點M′和點N′. 接著在線段MN上取兩點P，P，然后讓點P分別與P，P重合，找到點Q所在的位置P′，P′. 我發現點P′，P′恰好在線段M′N′上.

師：你們認為點Q的運動路徑是什么？

生（齊聲）：線段M′N′.

師生活動5：教師引導學生利用平板上的GeoGebra軟件作圖驗證，并利用平板的屏幕巡視功能及時查看學生的作圖情況，當學生遇到作圖難點時適時介入. 學生深刻體會作圖過程，積極分享對問題的認識.

師（發現作圖難點后）：作好線段MN和點A后，在線段MN上任取一點P，連接線段AP，接著如何作點Q呢？

生15：點Q可看作點P以點A為位似中心、按位似比縮小得到的. 首先點擊“變換—位似”的命令，接著依次選中點P（位似對象）和點A（位似中心），然后輸入（位似比），即可作出點Q.

生16：借助GeoGebra軟件的顯示軌跡功能，我拖動點P使其在線段MN上運動起來，點Q的運動路徑就直接顯現出來了. 可以看到，點Q的運動路徑是線段M′N′.

生17：借助GeoGebra軟件的度量長度功能，我度量出線段M′N′和線段MN的長度，然后借助GeoGebra軟件的數據計算功能，計算出=0.75，也就是M′N′=MN.

生18：因為點Q可看作點P以點A為位似中心、按位似比縮小得到的，所以點Q的運動路徑M′N′可看作點P的運動路徑MN以點A為位似中心、按位似比縮小得到的.

生19：位似不改變圖形的形狀，但會把圖形按照相應的位似比放大或縮小. 點P的運動路徑是線段，點Q的運動路徑也是線段（形狀相同），點Q的運動路徑的長度等于點P的運動路徑的長度乘.

3. 技術踏月留痕，尋跡領悟精髓

問題3? 結合問題1、問題2，談談動點路徑問題（雙動點旋轉位似類）的解題策略.

師生活動6：教師呈現問題3，告知學生動點P、動點Q可分別稱為“條件動點”和“目標動點”，然后讓學生思考后分享自己的想法.

生20：旋轉和位似都不改變圖形的形狀，所以條件動點P的路徑是“線”，目標動點Q的路徑也是“線”.

生21：兩點確定一條直線，因此要確定目標動點Q的路徑只需確定其路徑的兩個端點即可.

生22：旋轉不改變圖形的大小，但位似會改變圖形的大小，所以要計算目標動點Q的路徑長度，只需關注條件動點P到目標動點Q的變換中是否存在位似變換.

生23：若不存在位似變換，則目標動點Q的路徑的長度等于條件動點P的路徑的長度；若存在位似變換，則目標動點Q的路徑的長度等于條件動點P的路徑的長度乘位似比.

生24：如果條件動點P的路徑是“圓（圓弧）”，那么目標動點Q的路徑也是“圓（圓弧）”. 由于確定圓（圓弧）只需確定其圓心和半徑，因此確定目標動點Q的路徑只需確定圓心和圓（圓弧）上一點.

……

4. 深化思維印記，智慧引領創新

問題4? （2022年鼓樓二模第22題改編）如圖10所示，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，E為線段AB上一動點，∠ECF=90°且CF=CE，當點E從點B運動到點A時，點F的運動路徑的長為______.

師生活動7：教師呈現問題4，先讓學生獨立思考，再讓學生分享不同的解法.

學生解法1（通法）：如圖11所示，當點E分別與點B，A重合時，找到點F所在的位置F，F，則點F的運動路徑是線段FF. 連接CF，因為△FAC∽△ABC，且相似比為=，所以FF=AB=，即點F的運動路徑的長為.

學生解法2（巧法）：點F（路徑）可看作點E（路徑）先繞點C逆時針旋轉90°，再以點C為位似中心、按位似比縮小得到的. 所以點F的運動路徑的長為AB=.

教學反思

技術支持下的初中數學課堂教學是一種新型的教學模式，是未來教學發展的必然趨勢. 信息技術是深度探究的助推器，在讓學生更好地參與、體驗和感悟方面能發揮關鍵作用，真正實現課堂教學的創新. 要使信息技術與深度探究能夠融合發展，數學課堂教學應努力做到以下三點：

1. 全面搭建技術平臺，突破瓶頸尋覓本質

《義務教育數學課程標準（2022年版）》指出：“教學時可利用數學專用軟件等教學工具開展數學實驗，將抽象的數學知識直觀化，促進學生對數學概念的理解和數學知識的建構. ”借助數學專用軟件搭建技術平臺，能夠解決傳統教學不能解決的問題，快速尋覓問題的“根”與“本”. 在本節課中，當學生遇到探究瓶頸（無法盡可能多地在線段MN上取點）時，教師利用平板為全體學生全面搭建了繼續探究的平臺，引導學生利用平板上的GeoGebra軟件深入探究，在探究中尋覓并領悟動點問題的本質是圖形間的變換.

2. 有效加工邏輯組合，精準構圖全新建模

《教育信息化十年發展規劃（2011—2020年）》指出：“要利用信息技術開展啟發式、探究式、討論式、參與式教學，鼓勵發展性評價，探索建立以學習者為中心的教學新模式. ”在信息技術環境下，幾何探究式、課堂討論式、全體參與式教學可盡情開展，邏輯思維可奮起飛躍. 幾何語言包括文字語言、符號語言和圖形語言，理清三種語言之間的邏輯聯系是幾何教學的應然追求. 在本節課中，學生有效組合題干中的文字語言、符號語言和圖形語言，借助GeoGebra軟件的圖形變換功能完成精準構圖，這是對抽象問題全新建模的探究學習過程.

3. 多維開展實驗探究，深化思維彰顯通法

《義務教育數學課程標準（2022年版）》指出：“‘圖形的變化’應強調從運動變化的觀點來研究圖形，理解圖形在軸對稱、旋轉和平移時的變化規律和變化中的不變量. ”運用技術手段，數學實驗能夠“操作”起來，學生的思維也能“蹦跳”起來，解題方法自然就顯露出來了. 在本節課中，學生借助GeoGebra軟件，從圖形變換的視角開展實驗探究. 不同的學生探究的維度不同，但在實驗操作和交流分享中對問題都有了深層認識，學生的思維水平也在螺旋式上升，感悟出動點問題的通性通法，并能利用通法甚至巧法解決此類問題.

綜上所述，信息技術與深度探究可以融合發展，能收獲極佳的教學效果. 本文所述的教學課例，全面詮釋了信息技術與深度探究如何融合發展，它可以推廣到許多抽象的幾何問題的探究教學中，如“SSA”問題、將軍飲馬問題、圓周角定理證明、直線與圓的動態位置關系問題等. 積極開發技術支持下的教學范例，應成為一線教師的一項重要任務. 唯有如此，信息技術與深度探究才能更開放、更適合、更持久地融合發展.

作者簡介：崔豪東（1991—），本科學歷，中學二級教師，主要從事數學教育與信息技術融合研究，曾獲南京市數學基本功大賽一等獎、南京市數學優質課大賽一等獎.