稀疏軌跡毫米波雷達三維高分辨成像算法

馬宇欣 海 宇 李中余 黃 鵬 王朝棟 武俊杰 楊建宇

(電子科技大學信息與通信工程學院 成都 611731)

1 引言

隨著微波器件工藝和雷達系統技術的快速發展，毫米波雷達的應用得到了進一步的擴展。由于其優異的穿透性能[1]、較小的器件體積以及優異的成像分辨能力[2,3]，毫米波雷達被廣泛應用在安檢[4]、無損檢測[5]、醫學診斷[6]、自動駕駛[7]等領域。

毫米波雷達在應用于小目標成像識別時，為了達到多個維度的毫米級成像分辨，僅依賴發射高頻段大帶寬信號是難以實現的，因此許多學者提出了利用合成孔徑原理，通過在高度和方位向合成二維實孔徑的方式實現高的方位-高度分辨。根據成像分辨的計算式[8]，一方面，毫米波雷達通過發射中心頻率較高的大帶寬信號，利用增大帶寬提升距離分辨；另一方面，通過采樣操作，在方位向和高度向獲得大的合成孔徑同樣能提高分辨。

實際應用中，為了達到高分辨成像的目的，往往利用平臺搭載雷達，通過掃描合成大的方位-高度二維孔徑，實現高度向和方位向的二維高分辨。當毫米波雷達平臺通過多軌跡掃描采集回波數據時，增大軌跡間隔減少軌跡運動時間能降低操作的復雜度[9]，以上場景下采集的回波在高度維無法滿足奈奎斯特定理，具有稀疏特性。這就導致當采用傳統算法，如距離多普勒(Range Doppler,RD)、后向投影(Back Projection,BP)成像時，高度向的數據缺失會導致主瓣能量泄露、旁瓣抬升、目標混疊甚至無法成像。

為了解決該問題，常用的技術有壓縮感知[10-12](Compressive Sensing,CS)和矩陣填充[13,14](Matrix Completion,MC)，其中壓縮感知的概念于2006年被提出，它利用信號數據的冗余性，通過設計測量矩陣找到信號的稀疏表示，實現信號的稀疏恢復。在文獻[15,16]中，多次采用壓縮感知技術實現稀疏數據下的毫米波三維成像，但CS的稀疏恢復性能非常依賴測量矩陣的設計，當設計矩陣的稀疏基與場景中目標的分布不匹配時，恢復質量大打折扣。文獻[16]提出了結合深度學習的恢復成像方法，對傳統壓縮感知的迭代軟閾值算法(Iterative Soft Thresholding Algorithm,ISTA)展開設計unrolling網絡，通過網絡的訓練，學習符合場景的測量矩陣，能夠在數據稀疏度較大的場景高精度成像，不過網絡的訓練依賴大數量的樣本并且耗時較長。

不同的是，MC是一種利用數據的低秩約束恢復缺失數據的技術，目前已經應用在醫療成像[17]、稀疏信道估計[18]、陣列信號處理[19]等領域。MC具有效率高、恢復精度高等優點，因而也被用于解決稀疏成像的問題。文獻[20]提出了一種基于矩陣填充的二維稀疏毫米波三維成像方法，但矩陣填充技術不能從矩陣子集恢復原矩陣，即待恢復矩陣的每一行和每一列都要存在觀測信息，因而不適用于某一維度的大量缺失。文獻[21]提出了一種基于矩陣填充的稀疏線陣合成孔徑雷達(Synthetic Aperture Radar,SAR)成像方法，通過對信號切面矩陣做旋轉變換使得矩陣符合矩陣填充的工作前提，但由于僅考慮回波的低秩先驗，矩陣填充恢復效果不佳，不適用于高度向稀疏度較高的場景。

考慮到上述方法在應用于稀疏軌跡毫米波雷達成像中仍存在不足，本文提出了一種基于Hankel矩陣構造和矩陣填充的成像算法，實現了高稀疏軌跡下的毫米波雷達回波重構以及高分辨成像。本文的主要工作和創新點主要體現在以下3個方面：

(1) 構建了稀疏軌跡毫米波雷達的回波模型，并分析了回波的稀疏-低秩先驗特性，為成像算法的提出奠定了基礎；

(2) 提出了一種基于稀疏-低秩先驗的矩陣填充方法，利用回波高度-距離切面的稀疏-低秩特性，建立了基于截斷Scatten-p范數與l0范數的雙重約束優化模型，解決了傳統矩陣填充由于無法對行列缺失矩陣恢復從而無法直接應用于回波重構的問題；

(3) 提出了一種基于Hankel矩陣變換和矩陣填充的高精度成像方法，通過引入Hankel矩陣構造解決了高度向缺失度較高時難以實現高精度數據恢復的問題。

2 稀疏軌跡毫米波雷達回波建模與信號特性分析

2.1 稀疏軌跡毫米波雷達回波建模

根據引言的介紹，毫米波雷達在實際的應用中，存在通過手持或機械平臺搭載毫米波雷達掃描采集回波數據的場景，為了降低操作復雜度，通過增大軌跡間隔縮短軌跡時間，其掃描路徑往往稀疏不確定性，其幾何構型見圖1。經過孔徑校正后[22]，回波在方位向上均勻采樣而在高度向上非均勻稀疏采樣。其中X代表距離向，Y代表方位向，Z代表高度向，圖中的圓圈代表毫米波雷達稀疏軌跡采樣點，距離采樣點數為K，方位采樣點數為M，高度采樣點數為N′。

理想情況下，為了滿足奈奎斯特采樣定理，毫米波雷達在方位向和高度向的采樣點間隔需要小于等于半波長，三維回波采樣布局圖見圖2，稀疏軌跡孔徑校正后的高度向采樣點采樣間隔為半波長的整數倍，采樣點數為N′，符合奈奎斯特采樣定理的滿采情況下，高度向采樣間隔為半波長，所需的高度向采樣點數目為N，因此軌跡稀疏度為I=N′/N，兩種采樣布局的高度孔徑長度均為LN，因此理論可達的最高分辨一樣，而數據量相對減少1-N′/N。

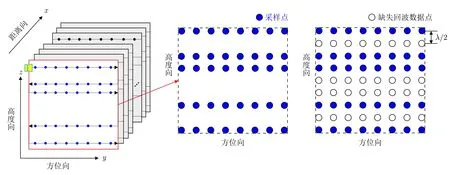
圖2 采樣布局圖Fig.2 Diagram of sampling layout

毫米波雷達由于工作頻段高，波長短，可以將目標視作多個散射點的集合。對于目標上的一個散射點Pp(xp,yp,zp)，采樣點Pr(x0,ym,zn)發射線性調頻信號，基于散射點模型，可以得到目標的回波信號表達式：

其中，t表示距離向時間，c是光速，fc是中心頻率，P為目標散射點總數，σp表示第p個散射體的反射系數，wr(·)表示距離向窗函數，λ為信號波長，Kr為信號調頻率，R(m,n,p)表示雷達采樣位置Pr(x0,ym,zn)到目標上散射點Pp(xp,yp,zp)的距離歷史，可以做以下近似：

其中，B是線性調頻信號的帶寬，由于不同方位和高度采樣過程是獨立的，通過對不同高度、方位的采樣點采集回波可以組合得到最終的三維回波形式S3D∈CK×M×N：

其中，Z={z1,z2,...,zN′}為掃描軌跡的高度向采樣點位置集合。

2.2 高度-距離切面信號的特性分析

同時，本節分析了采樣點間隔為半波長時，三維回波高度-距離切面信號的先驗特性。根據式(3)，對于第y0個方位時刻，經過距離壓縮、距離徙動校正后回波的高度-距離切面寫作：

其中，exp{-j2πfc(2R0/c)}常數可忽略，當在某一方位時刻時，exp[-j2π(/(λR0))]看作常數也可忽略，為了對式(5)中的高度-距離切面矩陣做進一步分解，對高度向的相位解耦合，即做相位補償，補償如下：

補償后的矩陣可以分解為

其中，T ∈CK×P,Γ ∈CP×P,Z ∈CP×N，具體表達式如下：

2.3 Hankel矩陣構造及特性分析

為了充分利用切面矩陣的低秩先驗特性以及高度向間相關性，引入Hankel構造變換，記作H(·)，變換示意圖見圖3。

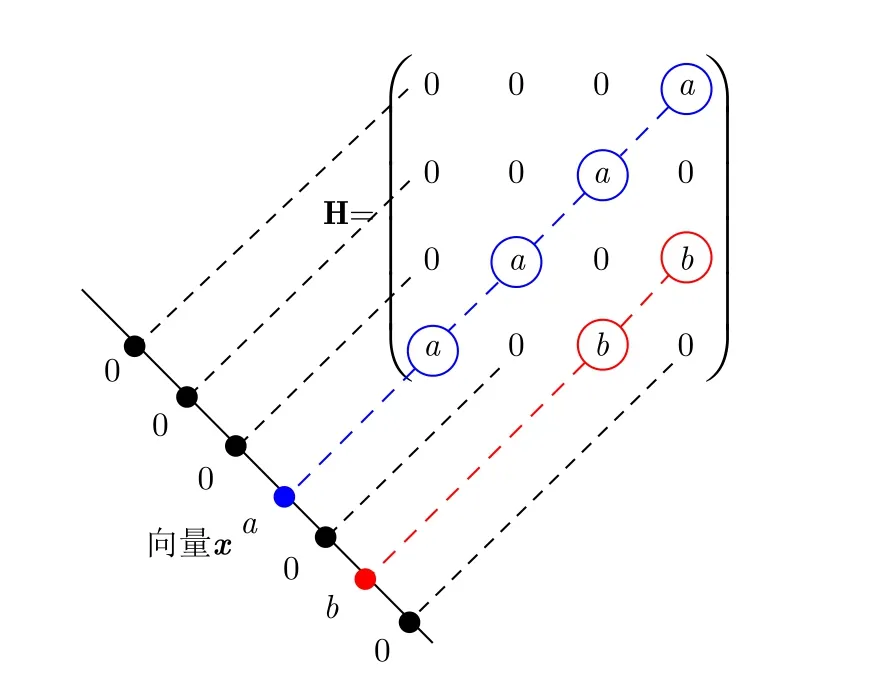
圖3 Hankel構造變換示意圖Fig.3 Diagram of Hankel structural transformation

取高度-距離切面矩陣中的距離單元向量做Hankel構造變換，高度-距離切面的距離單元向量記作SH(t0,y0,z)=[SH(z1),SH(z2),...,SH(zN)]∈C1×N，經變換后為

其中，C=sinc[B(t0-2R0/c)]可以看作常數，d是Hankel矩陣的間隔參數，經過Hankel構造變換后的矩陣維度為(N -d)×(d+1)。利用范德蒙德分解[23]，式(9)矩陣分解如下：

由于式(11)中各項頻率項相互獨立不同，并且r ?min{n1,n2}，Sfull是一個低秩矩陣，rank(Sfull)≤P。

除此之外，本文引入離散余弦變換(Discrete Cosine Transform,DCT)分析Sfull的稀疏性，DCT變換是在1974年由Ahmed等人[24]提出的，目前主要應用在圖像壓縮、音頻壓縮等領域，是一種類似于傅里葉變換的數學運算。當對Sfull做DCT變換時，變換后的矩陣幅度大小從左到右、從上到下遞減，數據主要集中在左上角區域，具有明顯的稀疏特性。綜合以上分析，取一個距離單元向量做Hankel構造變換后的矩陣具有稀疏-低秩先驗特性。除此之外，經過Hankel變換后的矩陣，具有更強的行列相關度。

3 一種基于Hankel-TSPN的三維成像方法

根據第2節的分析，滿采樣回波的高度-距離切面信號矩陣具有低秩性質，此外，對單個距離單元向量做Hankel構造變換可以增加待恢復矩陣的相關性，并且構造后的矩陣具有稀疏-低秩特性。

為了充分利用上述的低秩和稀疏先驗信息，本文介紹一種融合低秩和稀疏先驗的基于截斷的Schatten-p范數(Truncated Schatten-p Norm,TSPN)的矩陣填充算法，假設S ∈CM×N為一個距離單元向量做Hankel構造變換后的待恢復矩陣，建立優化模型：

其中，M是高度向稀疏采樣下觀測矩陣，μ>0是稀疏正則化參數，P?(·)是投影算子：P?(M)m,n=,? 是觀測矩陣的位置集合。由于低秩問題的求解是NP-hard的，這里采用截斷Schatten-p范數[25]逼近秩，相比傳統核范數可獲得更好的近似效果，優化問題轉化為

其中，tr(·)表示矩陣的跡，A,B是由S奇異值分解得到的，[A,Σ,B]=svd(S)，Ar和Br是通過對A,B取前r行得到，以達到截斷的效果。將以上問題轉化為無約束優化問題，對應的增廣拉格朗日函數為

其中，β是懲罰參數，Y,Z為拉格朗日乘子，ρ>1確保懲罰參數遞增。采用交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)[26]進行模型求解：

具體求解流程如下：

為了將變量X與變換算子DCT(·)分開，根據Parseval定理和DCT變換性質進行變換處理[27]，對式(17)應用逆變換可得

其中，IDCT(·) 是DCT(·)變換的逆變換，根據廣義軟閾值算法進行求解，通過已知參數，可得到閾值，如下所示：

對應的廣義閾值收縮方程如下：

對式(22)求偏導，令求導結果等于0，可得到Dk+1更新方程：

根據以上分析，得到聯合Hankel構造變換的TSPN矩陣填充算法流程，如算法1所示。該算法可以精確地實現回波高度-距離切面信號的重構。

為了對目標實現高分辨三維成像，通過循環方位向對高度-距離切面做Hankel-TSPN，實現對回波的三維重構，得到成像算法流程圖見圖4。

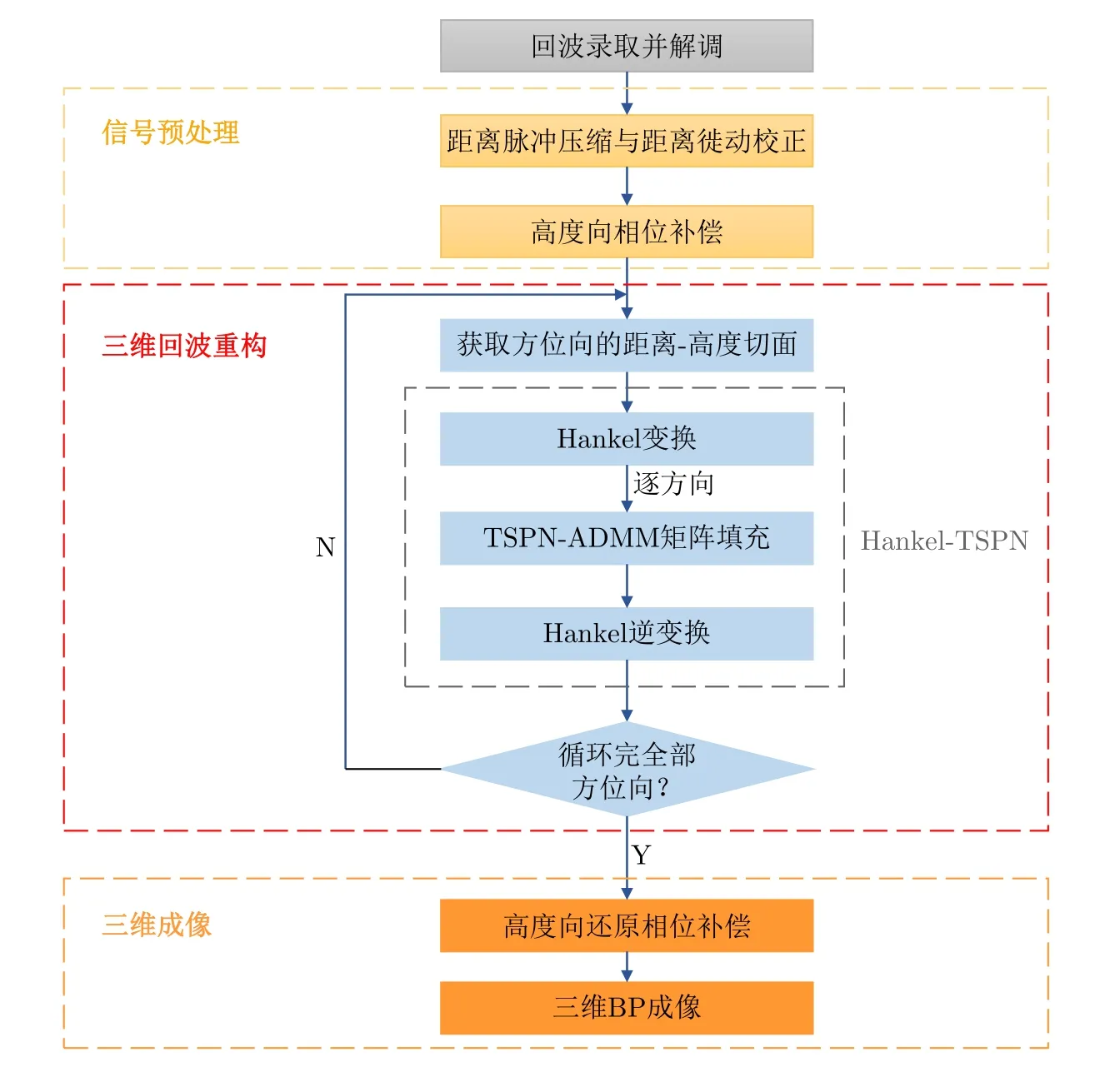
圖4 成像方法流程圖Fig.4 Flow diagram of imaging method

本文算法的核心在于利用回波的稀疏-低秩先驗特性建立優化模型，通過求解優化問題實現對三維回波重構，重構的三維回波相當于在方位-高度向上以半波長間隔采樣，從而提升成像質量。因此，從原理上講，本文算法同樣適用于高度向軌跡稀疏以外的其他缺失場景，如方位向稀疏采樣或高度-方位隨機缺失采樣。

4 仿真與實驗驗證

本節將通過點目標仿真和實測數據驗證上述稀疏軌跡毫米波雷達成像方法的性能，首先通過點目標仿真，初步驗證了算法的可行性；進一步采用本文提出算法對多組實測數據進行處理，并與傳統算法相比較，論證了算法的優越性。

算法 1 聯合Hankel變換的TSPN矩陣填充算法(Hankel-TSPN)Alg.1 TSPN matrix completion algorithm combined with Hankel transformation (Hankel-TSPN)

4.1 仿真實驗

為了驗證本文方法的有效性，首先設置多點目標仿真，仿真參數如表1所示，點目標布局如圖5(a)所示，共有5個點目標位于同一YOZ平面，每個點目標均具有相同的散射系數，采用BP算法處理成像結果見圖5。

表1 仿真參數Tab.1 Simulation parameter

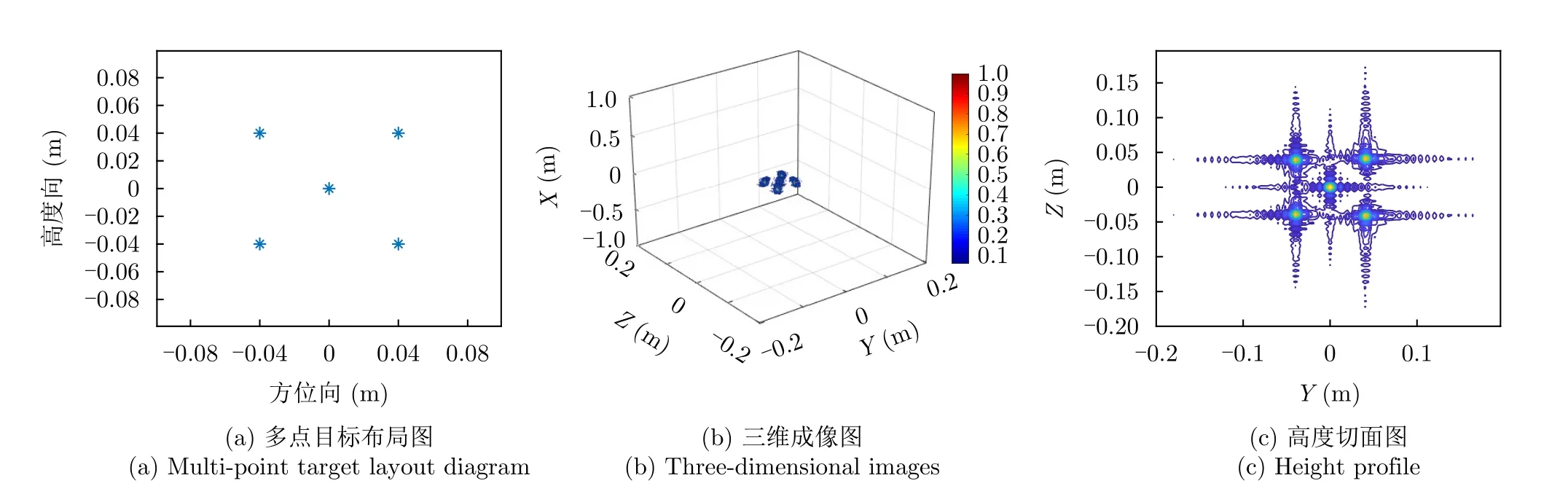
圖5 多點目標布局及成像圖Fig.5 Multi-point target layout and imaging diagram

首先，利用仿真驗證Hankel-TSPN算法的優越性，TSPN算法由于結合了稀疏先驗，解決了傳統矩陣填充無法對行列缺失等結構性缺失矩陣恢復的問題，并且聯合Hankel矩陣構造后可以進一步提升對矩陣的重構恢復效果。本文將本方法與一些經典的矩陣填充算法進行了對比。圖6比較了奇異值閾值算法(Singular Value Thresholding,SVT),TSPN和Hankel-TSPN對一個高度-距離切面矩陣的恢復效果。從圖中可以看出SVT算法由于僅考慮低秩先驗無法對行缺失矩陣做恢復，低秩-稀疏先驗的TSPN算法可以對行缺失矩陣一定恢復，但恢復效果不佳，而Hankel-TSPN恢復結果與原圖基本一致。

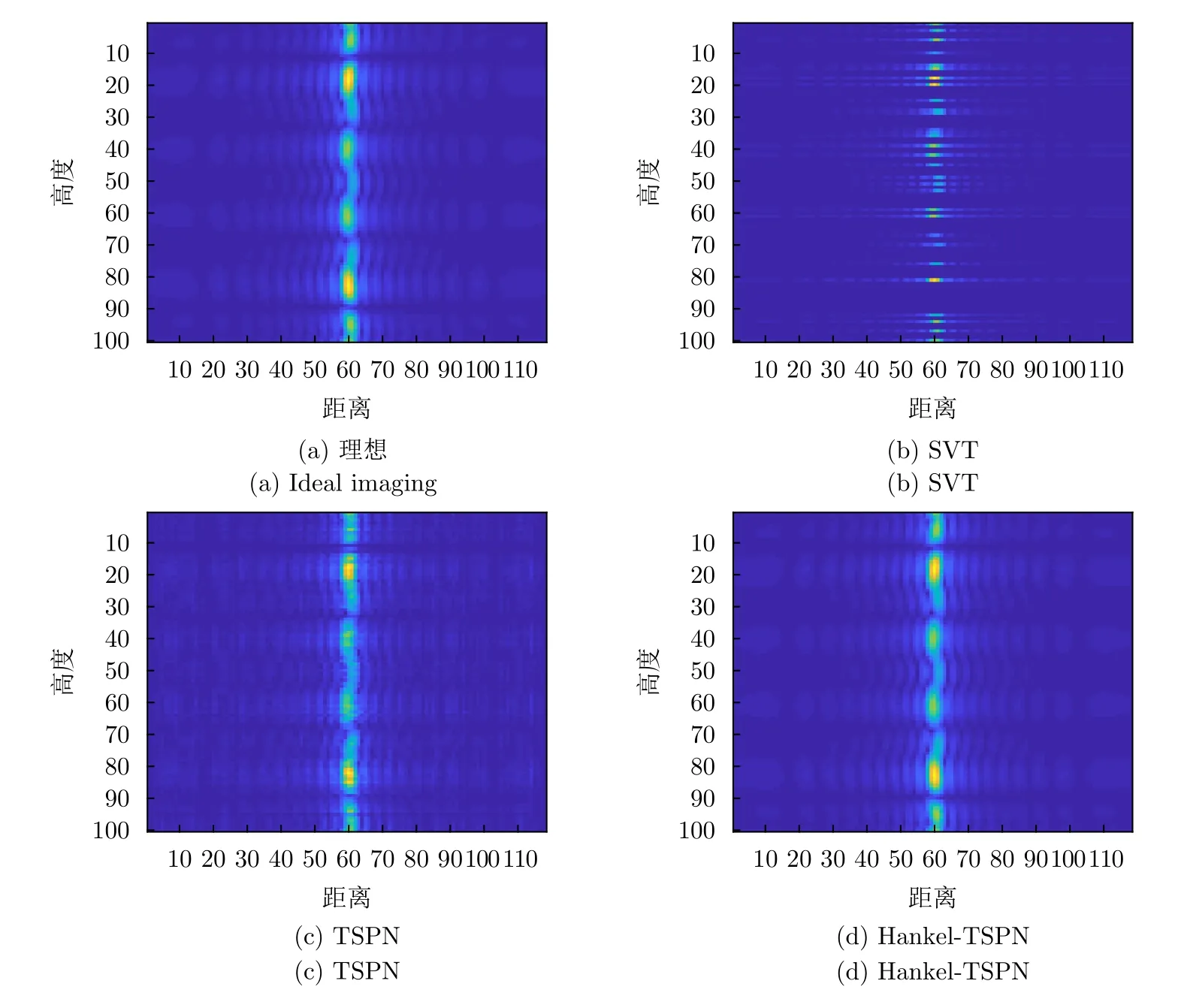
圖6 不同方法的高度-距離切面矩陣恢復圖Fig.6 Different methods of height-distance section matrix restoration

進一步，分別采用30%,20%,10%稀疏軌跡驗證本文方法的成像質量，圖7給出了不同稀疏度的稀疏軌跡直接3D-BP成像結果和基于Hankel-TSPN的成像結果，圖7(a)的軌跡稀疏度為30%；圖7(b)軌跡稀疏度為20%；圖7(c)軌跡稀疏度為10%。當直接利用稀疏軌跡回波BP成像時，在高度維會出現嚴重散焦，而采用本文所提出的基于Hankel-TSPN的算法成像時，目標清晰可分辨，且目標能量得到聚焦。

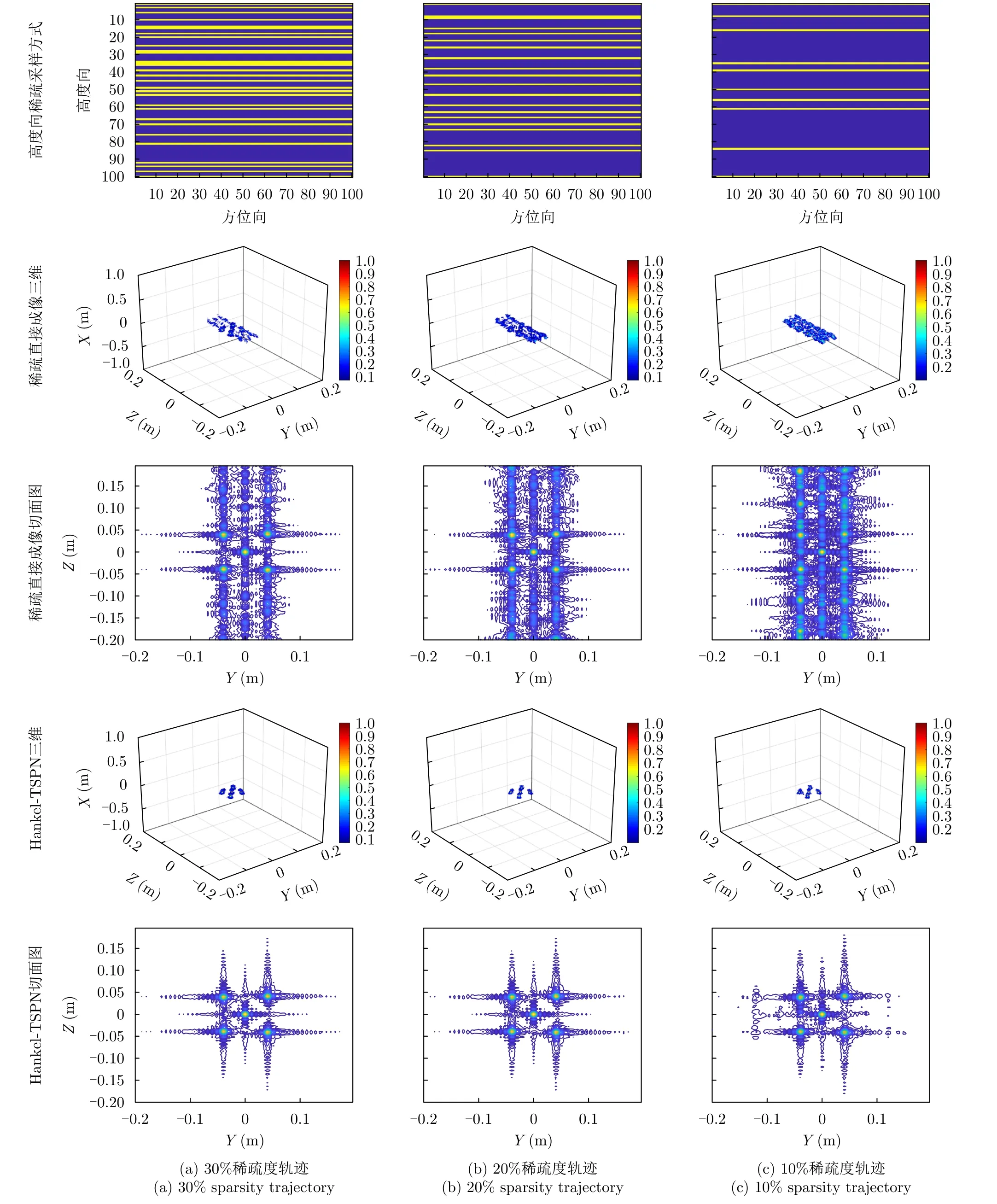
圖7 點目標不同稀疏度軌跡下成像結果Fig.7 Imaging results of point targets with different sparsity trajectories

圖8中，利用20%稀疏軌跡下單點的成像做高度向剖面圖分析，當采用本文提出的方法處理時，目標旁瓣得到了有效的抑制。除此之外，圖8中不同算法處理的信號剖面可以用峰值旁瓣比(Peak side lobe ratio,PSLR)和積分旁瓣比(Integral side lobe ratio,ISLR)兩個指標進行分析，結果見表2，可以直觀地說明采用本節方法處理后的回波成像結果具有更高的聚焦度。

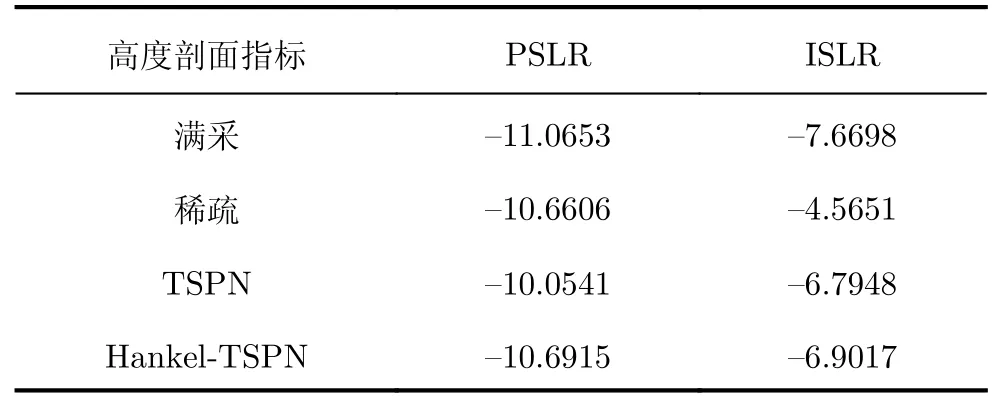
表2 20%稀疏軌跡下高度剖面的峰值旁瓣比與積分旁瓣比(dB)Tab.2 Peak sidelobe ratio and integral sidelobe ratio of height profile at 20% sparse trajectory (dB)

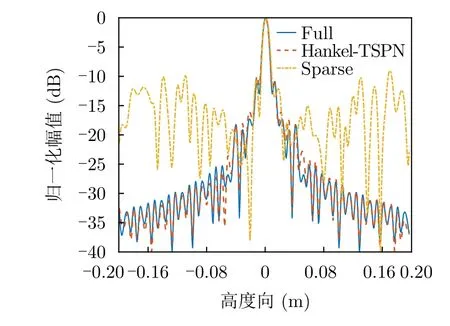
圖8 20%稀疏軌跡下中心點高度剖面對比圖Fig.8 Height profile comparison of center points under 20%sparse trajectory

4.2 實測實驗

為了進一步驗證算法的優越性，對實測數據進行成像，目標是一個直徑為8 cm的檸檬芯，回波信息通過THz通感一體(Integrated Sensing and Communication at THz band,ISAC-THz)樣機獲得[28]，圖9給出了目標與樣機示意圖，實驗參數見表3。

表3 檸檬芯實測目標參數Tab.3 Lemon core measured target parameter

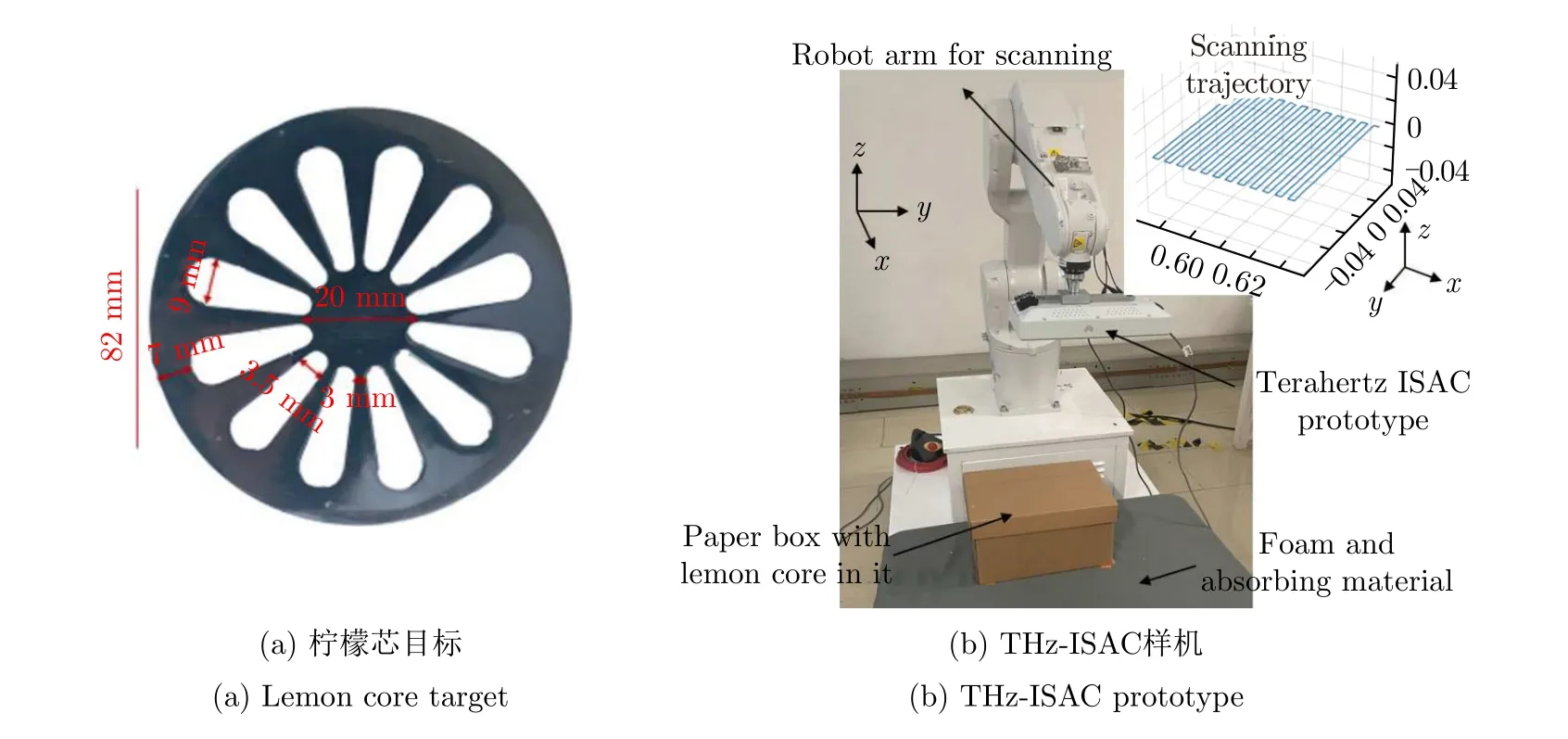
圖9 系統及目標示意圖[28]Fig.9 System and target diagram[28]

考慮稀疏軌跡場景，稀疏度為20%的高度向軌跡位置見圖10，同一稀疏軌跡采樣方式不同方法的成像結果見圖11，圖中分別比較了理想成像、20%稀疏軌跡BP成像、壓縮感知和本文算法的成像結果，其中壓縮感知采用的是迭代最小稀疏貝葉斯重構

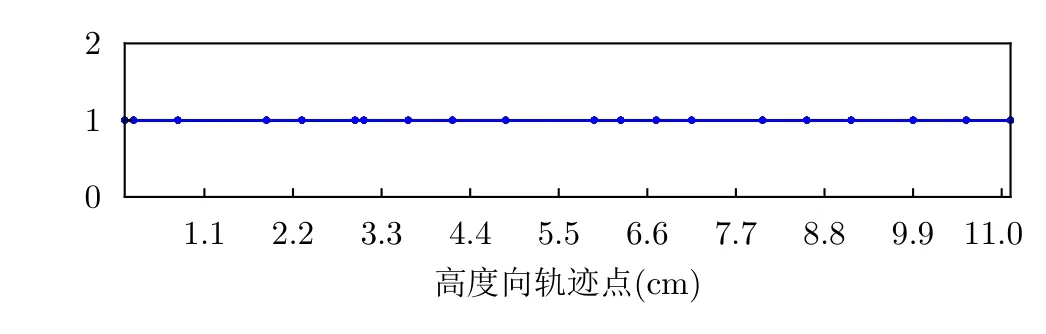
圖10 稀疏度為20%的稀疏軌跡位置示意圖Fig.10 Location diagram of sparse trajectory with a sparsity of 20%

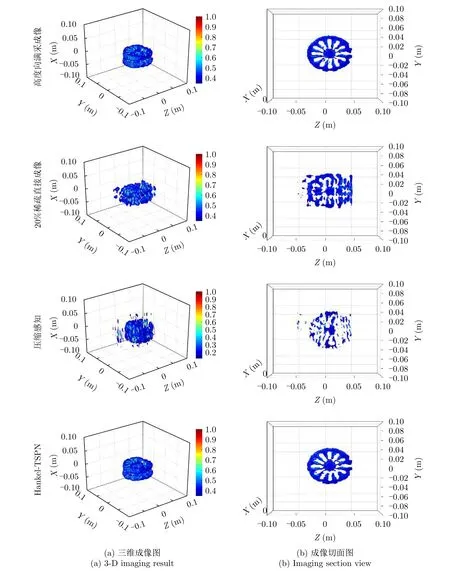
圖11 檸檬芯成像圖Fig.11 Images of lemon core

(Sparsity Bayesian Recovery via Iterative Minimum,SBRIM)[29]，該算法在較多實測數據應用場景下均能有較好的成像質量。除此之外，傳統壓縮感知方法在對稀疏實測數據處理時，依賴稀疏基的設計，需要場景與目標的先驗信息，對未知場景與目標的成像效果較差，而本文所提方法充分利用回波的先驗特性，通過對回波先補全再成像的方式，可以保證三維成像精度，由此驗證了本文算法的優勢。

表4給出了檸檬芯方位-高度切面圖的圖像質量比較，表中分別從對比度、銳度和圖像熵3個角度衡量圖像質量，并采用結構相似度(Structural Similarity,SSIM)衡量不同方法在不同采樣稀疏度下的成像結果相似度，其中采用本文方法獲得的成像結果較于傳統的壓縮感知算法更好，且更接近滿采的成像結果。由此可見，本文方法在對實測數據進行處理時，仍能有很好的成像效果。

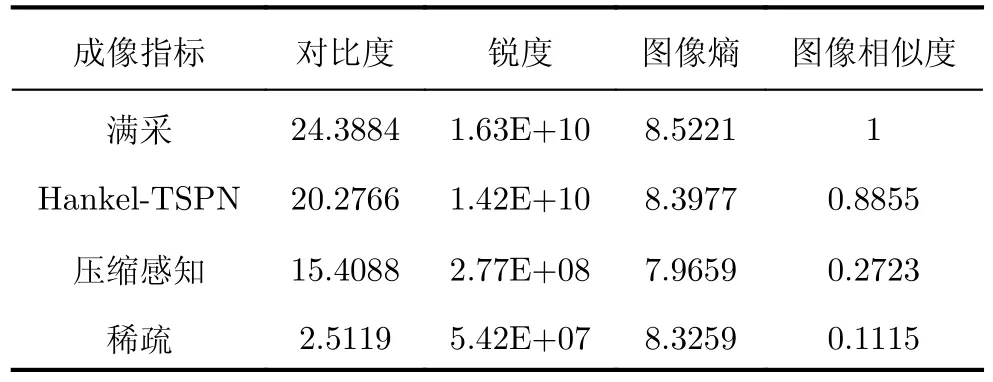
表4 三維方位-高度切面圖圖像質量比較Tab.4 Comparison of image quality of 3D azimuth-height slice

除此之外，為了驗證本文方法的魯棒性，利用高分辨三維毫米波雷達數據集[30]，對幾種復雜體目標做了進一步的驗證。數據集獲取模式為毫米波傳感器沿二維平面掃描進行近場成像，掃描尺寸大小為0.4 m×0.4 m，雷達中心頻率為78.8 GHz，發射信號帶寬為3.6 GHz。不同稀疏度的采樣方式見圖12，圖13給出了不同方法的成像圖。

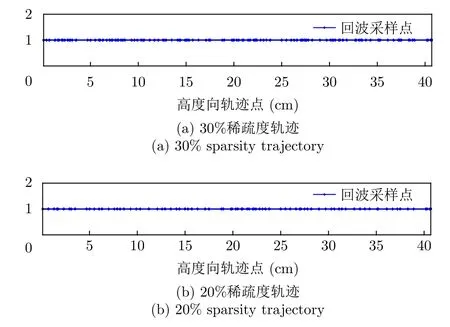
圖12 不同稀疏度的稀疏軌跡位置示意圖Fig.12 Location diagram of sparse trajectory with different sparsity

圖13 不同目標不同稀疏軌跡下成像結果圖Fig.13 Imaging results of different targets with different sparse trajectories

通過圖13可知，本文方法在僅使用20%～30%的高度向數據時，便能實現接近滿采的成像效果，當高度向為稀疏軌跡時，傳統BP成像結果中成像目標的對應維度散焦。對不同場景的不同目標做成像，采用本文方法均能獲得較高分辨的成像結果，由此體現了本文方法的優越性及廣泛的適應性。

最后，本文對該方法的計算量進行了分析，設三維回波矩陣為RK×M×N，K為距離向采樣點數，M為方位向采樣點數，N為按半波長劃分的高度向采樣點數，投影矩陣的大小為Dx×Dy×Dz，不同算法的計算復雜度見表5。以檸檬芯實驗為例，采用3D-BP成像需要332 s，采用基于SBRIM的壓縮感知需要524 s，而采用本文算法需要618 s。因此本文算法和CS,BP在運算量上屬于同一量級，但本文算法相比其他算法可以實現更高稀疏度下的高精度成像。

表5 不同算法的計算復雜度Tab.5 Computational complexity of different algorithms

5 結語

傳統毫米波雷達為了實現高分辨三維成像，面臨著操作復雜度高、數據量大、成本高的問題。本文主要針對，由平臺掃描導致的稀疏軌跡構型。該構型通過增大軌跡高度維間距，縮短軌跡掃描時間，降低成像復雜度，然而高度維稀疏會導致成像散焦。本文提出了一種適用于該構型的三維高分辨成像方法。不同于傳統的壓縮感知算法，本文從回波特性入手，首先分析了回波的低秩-稀疏先驗特性，因此構建優化模型并采用ADMM求解得到TSPN算法，進一步引入Hankel矩陣構造，增加待恢復矩陣的行列相關性，得到了一種基于Hankel-TSPN的成像算法，有效解決了傳統算法對于單一維度高稀疏度下恢復成像效果不佳的問題。最后，本文通過一系列的實測數據處理驗證了在軌跡稀疏度20%以上的場景，采用本文方法均能得到良好的成像結果，并通過與其他算法成像比較，充分體現了本文方法的優越性。