改進的粒子群優化算法在云計算任務調度中的應用
汪婷, 邵鵬, 李光泉, 劉珊慧
(江西農業大學計算機與信息工程學院, 南昌 330045)
云計算(cloud computing,CC)是以互聯網為核心,根據用戶需求,動態存儲、整合相關資源,向用戶提供高性能服務的一種新興技術。調度技術作為云計算的關鍵技術,能夠對物理資源進行高效管理,以獲得更好的資源配置方案。Bisht等[1]綜合考慮異構環境下的成本、最大完成時間等因素,提出改進Min-Min工作調度算法。Alworafi等[2]基于最短作業優先,以最小化任務完成時間和平均響應時間為目標提出改進算法,同時最大化資源利用率。Alhuidari等[3]利用輪詢算法,根據時間量子平均值自適應更新,提高云計算系統吞吐量。然而,傳統的先來先服務、短作業優先等確定性調度算法因時間開銷大,可靠性低,通常無法獲得最佳調度方案。
現有方法表明,啟發式算法可通過預測獲得時間復雜度低的近似最優解[4]。Liu等[5]針對云計算任務調度中普遍存在的資源利用率低這一缺點,提出基于不同信息顆粒的貪心調度策略,并針對不同特征的任務分配不同的調度策略。由于處理任務的成本和能耗較高,啟發式算法不適用于處理云計算任務調度問題。而元啟發式算法能夠在不預先告知任務和資源的條件下直接獲得最優解,且結果優于啟發式算法,因此被廣泛用于求解云計算任務調度問題,包括鯨魚優化算法[6]、遺傳算法[7-9]、人工蜂群算法[10-11]以及粒子群優化算法[12-14](particle swarm optimization,PSO)等。其中,PSO算法是Kennedy和Eberhart于1995年提出的基于群體協作的隨機搜索算法,具有原理簡單、收斂速度快等特點,被認為是求解云計算任務調度問題最具潛力的方法之一。
從已有的研究成果中可以發現,傳統PSO算法在求解云計算任務調度問題中存在收斂速度慢、精度低等缺陷[15]。Dubey等[16]受化學反應優化算法啟發,通過迭代算子保存具有高適應度值的次優解,并用于下一次迭代,以提高PSO算法解的質量,加快粒子收斂速度。張思豪等[17]引入資源狀態指標,分批處理任務尋求最優解,縮短任務完工時間。Nanjappan等[18]通過冠狀模糊均值算法對獨立任務進行聚類并調度至各虛擬機中執行,最后通過PSO算法計算特征值,有效提高結果精度。馬學森等[19]提出一種多策略融合的改進PSO算法,首先引入非線性慣性權重策略提高粒子尋優能力,接著通過花朵授粉算法平衡算法的探索與開發,最后利用螢火蟲算法產生“精英解”對粒子位置進行擾動,跳出局部收斂,改進算法在收斂速度和精度上都獲得明顯提升,但存在尋優效率低等問題。因此孫長亞等[20]利用動態更新慣性權重策略提高PSO算法的自適應搜索能力,同時引入微生物遺傳算法,在算法前期縮小目標搜索空間,并在算法后期利用PSO算法快速收斂,獲得全局最優解,提高算法尋優效率。
此外,為降低算法陷入局部極值的概率,Nabi等[21]基于線性遞減自適應慣性權重策略提出一種自適應粒子群優化算法,以平衡算法的局部搜索和全局搜索能力,避免算法陷入局部極值。朱琳等[22]采用非線性遞減慣性權重更新策略提高算法后期收斂能力。譚鶴毅等[23]利用天牛須搜索算法實現多個個體同步計算,提高種群間信息交互能力,幫助粒子跳出局部極值。盡管眾多學者針對PSO算法在求解云計算任務調度問題中存在的收斂速度慢、精度低、易陷入局部極值等缺陷,分別開展了大量的研究工作并且提出了相應的改進算法。然而,針對PSO算法存在的以上3種缺陷進行同時改進,并將其應用于求解云計算任務調度問題,仍將是一個極富挑戰的任務。
綜上,針對PSO算法在求解云計算任務調度問題上的缺陷,綜合考慮最大完成時間最少、任務執行總時間最優兩個優化目標,在PSO算法中融合模擬退火算法[24](simulated annealing, SA)、饑餓游戲搜索[25](hungary games search,HGS)及雙重變異限制策略[26](double restrictions),現提出一種融合多種策略的粒子群優化算法(multi-strategy particle swarm optimization, MSPSO)。引入模擬退火算法動態更新粒子慣性權重,平衡算法的探索和開發,避免算法陷入局部極值。引入饑餓游戲搜索算法優化粒子位置更新策略,加快粒子收斂速度,提高結果精度(更優數量級)。引入雙重變異限制策略同時限制粒子速度和位置,避免粒子發生越界,提高算法尋優效率。將所提算法MSPSO應用于求解云計算任務調度問題,在不同任務量下進行對比實驗,以驗證MSPSO算法在實際應用中的可靠性和實用性。
1 云計算任務調度描述
云計算是一種全新的、基于并高度依賴Internet、自助式使用遠程計算資源的技術,具有按需服務、動態可拓展、虛擬化等特點,它主要包括3種服務模式:基礎設施即服務(IaaS)、平臺即服務(PaaS)和軟件即服務(SaaS)。通常在云計算環境中,一個用戶任務被切分成n個不同大小、相互獨立的子任務,子任務集合可以用字母N表示為:N={n1,n2,…,nn},假設所有的子任務被分配到m個虛擬機上執行,虛擬機擁有CPU、內存、存儲等資源,用VM表示為:VM={vm1,vm2,…,vmm}。其中,n>m,ni(1≤i≤n)表示第i個任務,vmj(1≤j≤m)表示第j個虛擬機。任務調度即將n個子任務調配到m個虛擬機中執行,并獲得最佳調度方案,實現任務執行的最大完成時間最小、任務執行總時間最優等目標。云計算任務調度的框架可簡化為圖1。

圖1 云計算任務調度框架Fig.1 Cloud computing task scheduling framework
為了便于計算每個任務完成調度所需要的時間,分別定義一個n×m的矩陣E,T。其中,E為子任務在各虛擬機上的執行時間矩陣,如式(1)所示。T為將子任務數據傳輸到各虛擬機上的傳輸時間矩陣,如式(2)所示。
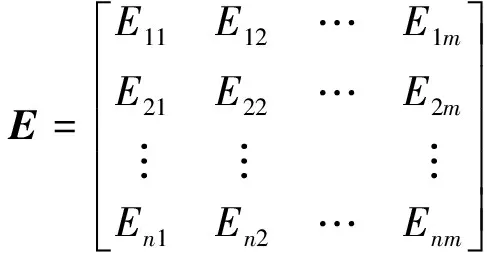
(1)

(2)
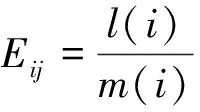
2 多策略融合的粒子群優化算法
2.1 粒子群優化算法
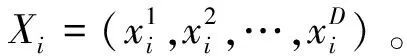
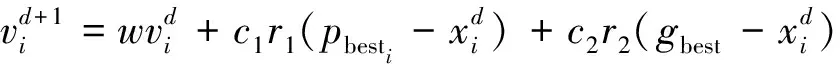
(3)
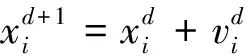
(4)
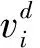
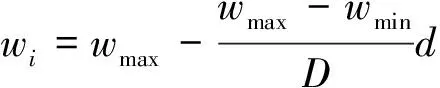
(5)
式(5)中:wmax為最大慣性權重;wmin為最小慣性權重。
2.2 改進的粒子群優化算法
為克服PSO算法在求解云計算任務調度問題中存在的早熟收斂、易陷入局部極值等缺陷,基于PSO算法,融合饑餓游戲搜索、模擬退火算法和雙重變異限制策略,提出了一種多策略融合的粒子群優化算法MSPSO,運行機制如圖2所示。首先使用模擬退火算法動態更新慣性權重,平衡算法的探索與開發;其次通過饑餓游戲搜索優化粒子的位置更新策略,加快粒子收斂速度,提高結果精度;最后采用雙重變異限制策略防止粒子越界,提高算法尋優效率。
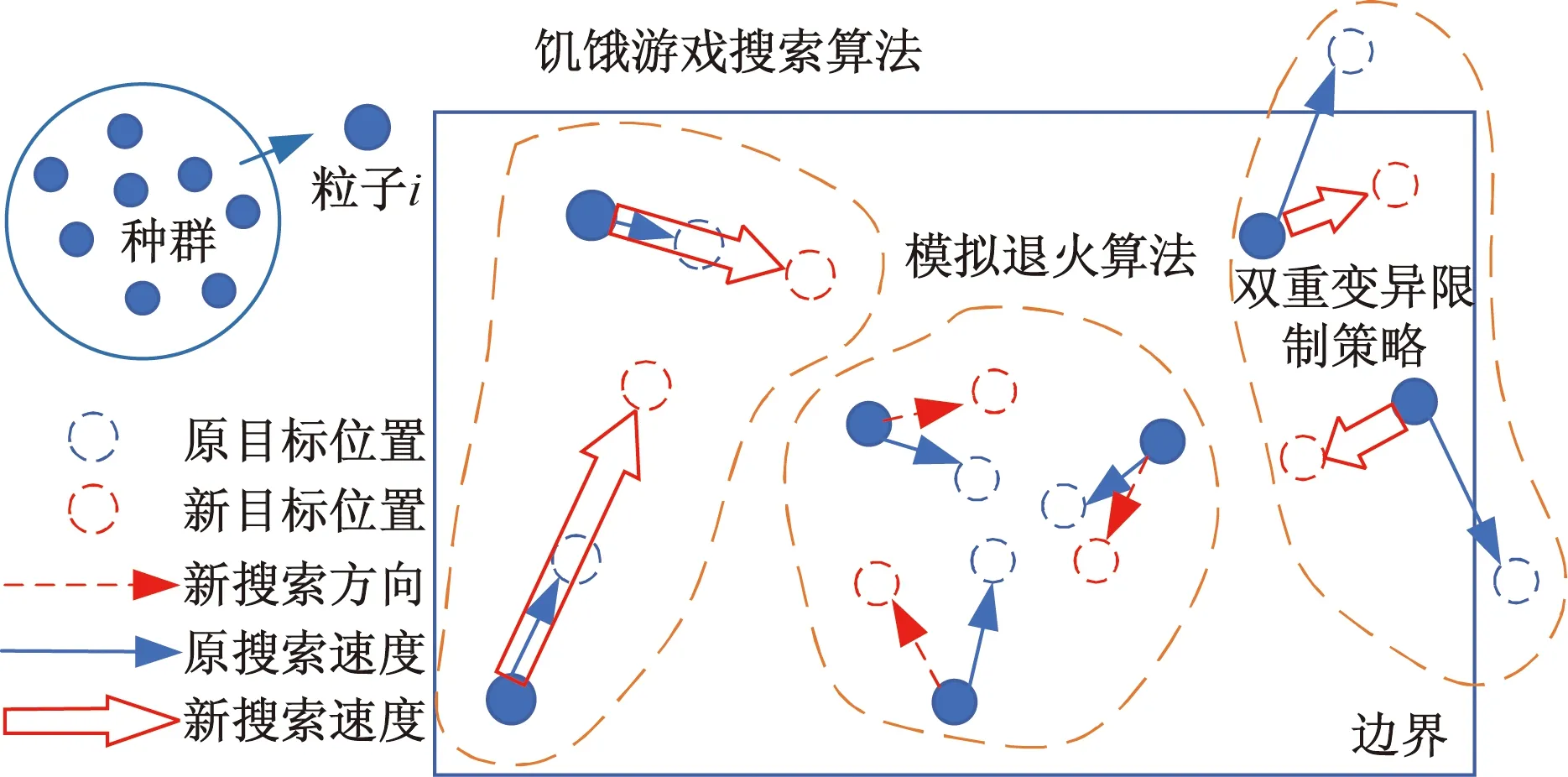
圖2 MSPSO算法的運行機制Fig.2 The operation mechanism of MSPSO algorithm
2.2.1 慣性權重更新策略
在MSPSO中,首先隨機初始化粒子的位置和速度,通過計算粒子適應度值,獲得全局最佳位置gbest和局部最佳位置pbest。慣性權重w是PSO算法的重要參數之一,當w較大時,算法的全局尋優能力增強,粒子更容易跳出局部極值,但同時會降低搜索效率,不易收斂;反之亦然。模擬退火算法[24]是一種基于概率的算法,通過設置模擬退火概率P來動態調整慣性權重。若當前迭代次數t是正整數k的整數倍時,調用模擬退火算法,慣性權重更新公式為
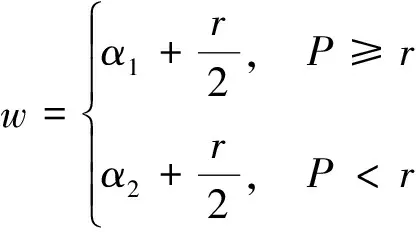
(6)
式(6)中:α1、α2為[0,1]內常數,且α1>α2;r為[0,1]內常數,模擬退火概率P公式為
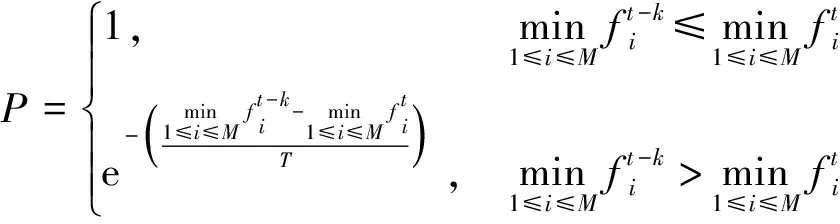
(7)
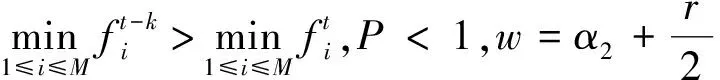
2.2.2 位置更新策略
饑餓游戲搜索算法[25]受動物社會行為的影響,將個體的饑餓程度h作為個體饑餓特征進行數學模擬。將算法用于優化粒子位置更新策略,可以提高粒子間的信息交互能力,在算法后期加快粒子的收斂速度,改進后的粒子位置公式為
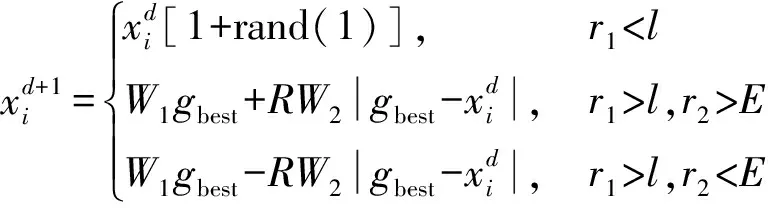
(8)
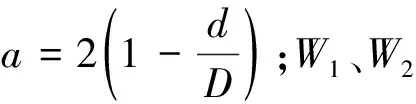
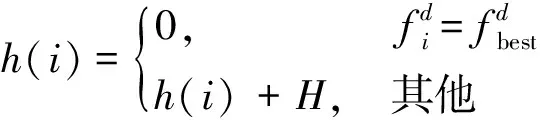
(9)
2.2.3 邊界限制策略
PSO算法在搜索空間尋找最優解過程中,容易發生粒子越界。在已有研究中,大部分策略采用限定粒子位置、降低粒子飛行速度等方式限制粒子行為,然而當粒子飛出搜索空間且速度很大時,只限制粒子位置而不降低粒子速度,仍可能發生越界行為。采用雙重變異限制策略[26],可同時限制粒子位置和速度,將粒子控制在搜索空間內,其限定因子χ公式為

(10)
式(10)中:φ=0.5。則χ被限制在[0,0.5]范圍內,可有效解決算法由于加入過多隨機性而導致的收斂速度過快和收斂精度不足的問題。
MSPSO的偽代碼如表1所示。現對MSPSO的時間復雜度進行分析,標準粒子群優化算法的時間復雜度為O(M×Tmax×D),其中M為粒子總數,Tmax為最大迭代次數,D為維度。慣性權重更新策略、位置更新策略、邊界限制策略為O(M×D),故MSPSO的時間復雜度約為O(M×Tmax×D)。

表1 MSPSO的偽代碼
3 MSPSO算法性能對比
為驗證所提算法的優越性,分別在30、50、100、1 000共4種維度下,將MSPSO算法與PSO、QUAPSO[27]、ADPSO[21]這3種算法進行對比實驗,其參數設置為:粒子總數M=100、最大迭代次數Tmax=500。考慮到粒子群優化算法的隨機行為,在運行100次后取平均值作為最終結果。
選取了13個基準測試函數驗證所提算法的有效性,如表2所示,其中f1~f5為單模態函數,f6~f10為多模態函數,f11~f13為固定維數函數。

表2 基準函數
為了評估算法的效率和性能,分別從適應度平均值Avg、最小值Min、標準差SD 3個方面進行評估。表3為各算法在求解高維問題(D=1 000)時獲得的適應度Avg、Min、SD。
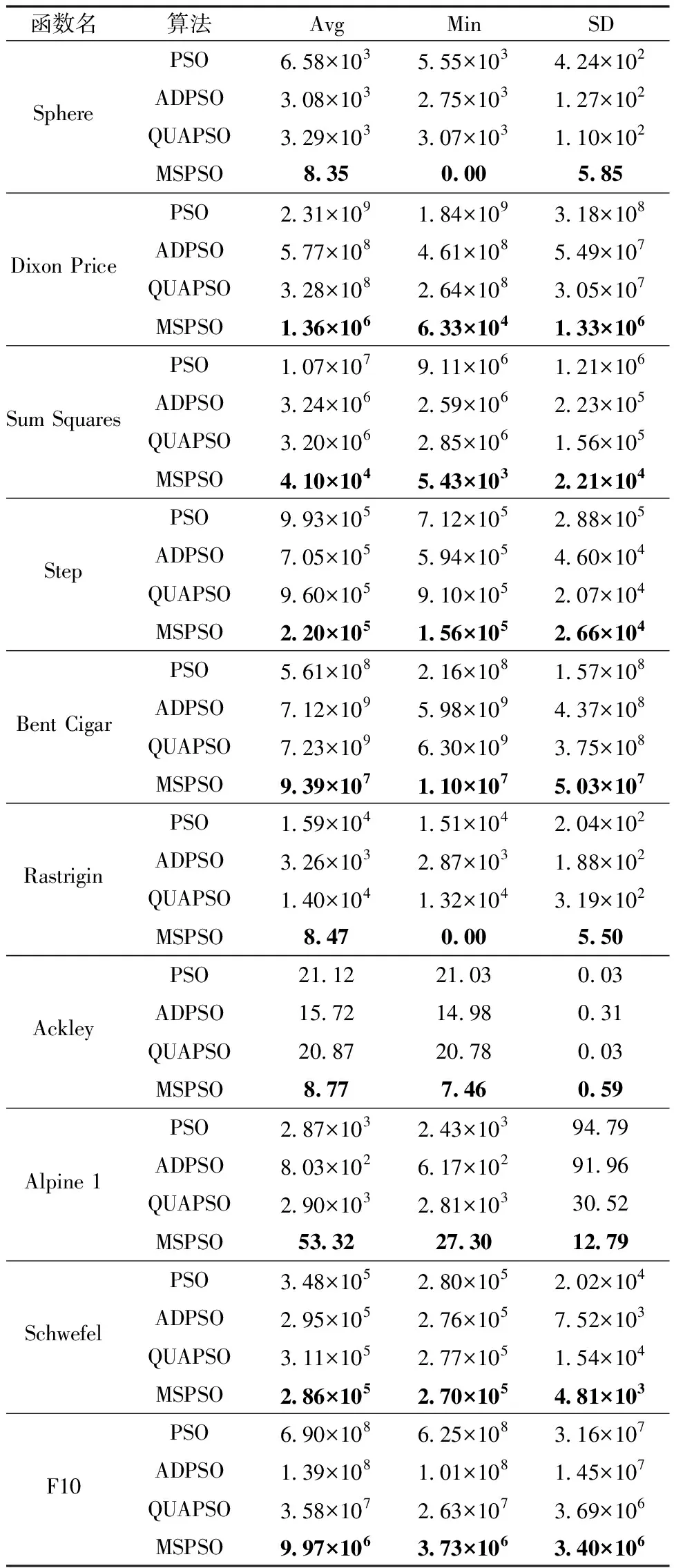
表3 各算法求解高維問題的最優值統計
如表3所示,在求解單模態問題f1~f5時,MSPSO算法相比其他算法,能夠獲得更優數量級的最優解。以Dixon Price函數為例,MSPSO適應度平均值分別比PSO、ADPSO、QUAPSO低99.94%、99.76%、99.58%,最小值低99.99%、99.98%、99.97%,標準差低99.58%、97.57%、95.63%。這得益于饑餓游戲搜索算法在MSPSO算法后期引導最優粒子快速靠近全局最優解,加快算法收斂速度,提高結果精度。在求解多模態問題f6~f10時,MSPSO相比其他算法,同樣可以獲得更優解,表明MSPSO算法中慣性權重更新策略在保持種群多樣性,平衡算法的探索與開發方面效果顯著。圖3表示當維度D=1 000時,各算法在Sphere、Dixon Price、F10中的適應度平均值對比,可以看出MSPSO在收斂性、跳出局部極值等方面都明顯優于其他算法。各算法求解低維(D為30、50、100)及固定維數問題獲得的適應度Avg、Min、SD如表4所示。
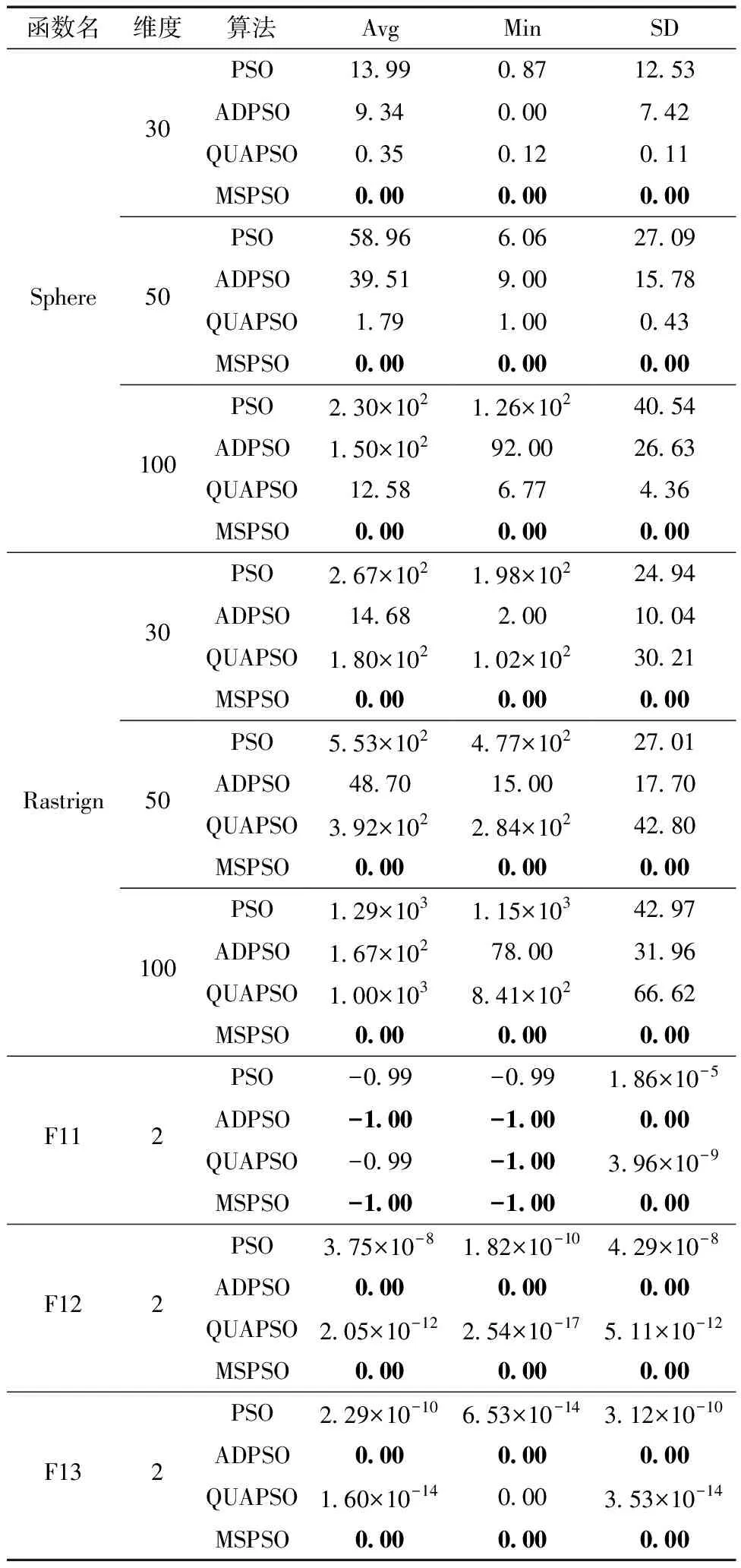
表4 各算法求解低維及固定維數問題的最優值統計
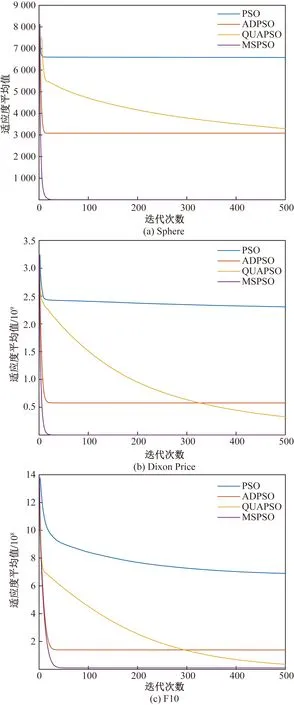
圖3 各算法在3個基準函數中的適應度平均值對比Fig.3 Comparison of the fitness of each algorithm in three benchmark functions
4 MSPSO用于云計算任務調度
4.1 粒子編碼
PSO算法是一種解決連續問題的元啟發式算法,將其應用于求解任務調度問題,首先需要構建有效的粒子編碼方案。采用間接編碼方式,設粒子位置編碼長度為子任務個數,一個子任務對應一個虛擬機。舉例說明,若子任務數N=10,虛擬機數VM=5,則粒子i的位置編碼長度為10,可以表示為xi={2,4,5,1,3,4,2,5,1,4},其第1位編碼表示子任務n1在虛擬機vm2上執行,第2位編碼表示子任務n2在虛擬機vm4上執行,依此類推。其映射關系如表5所示。

表5 子任務與虛擬機間映射關系
4.2 適應度函數設計
綜合考慮最大完成時間最小、任務執行總時間最優兩個優化目標,MSPSO的數學模型描述如下。
定義1任務執行總時間。
任務執行總時間Tsum指按調度方案,各虛擬機完成其分配子任務的總時間,Tj表示虛擬機VMj完成分配子任務的總時間,公式如下。
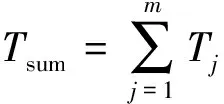
(11)
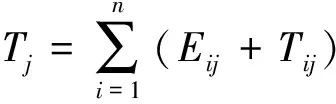
(12)
定義2最大完成時間。
任務的最大完成時間Tmax表示最后一個子任務的完成時間,公式為
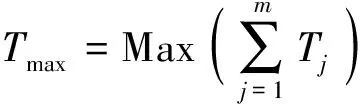
(13)
適應度函數由式(14)獲得。
Fitness=αTsum+(1-α)Tmax
(14)
式(14)中:α為優化目標對適應度函數的影響權重。將云計算任務調度問題轉變為找到適應度最小值的任務調度方案。
4.3 任務調度流程
融合多策略粒子群優化算法的云計算任務調度部署流程如下。
步驟1初始化云計算數據中心的物理主機列表和虛擬機列表。
步驟2初始化算法參數,設置慣性權重w、最大迭代次數Tmax、常數l等。
步驟3粒子編碼,初始化粒子位置和速度。
步驟4迭代次數t=t+1。
步驟5根據式(14)計算粒子適應度值,更新gbest和pbest。
步驟6維度d=d+1。
步驟7判斷當前迭代次數t是否為正整數k的整數倍,若是,則調用隨機慣性權重策略根據式(6)動態更新慣性權重w,否則根據式(5)更新。
步驟8根據式(3)更新粒子速度。
步驟9判斷當前維度d是否為整數z的整數倍,若是,則調用饑餓游戲搜索算法,根據式(8)更新粒子位置;否則調用式(4)。
步驟10更新后,粒子的編碼序列范圍可能超出設定閾值,此時調用雙重變異限制策略,同時限定粒子位置和速度,防止粒子發生越界。
步驟11若當前維度d 步驟12若當前迭代次數t 使用Cloudsim模擬云計算環境,包括數據中心、物理主機、虛擬機及云服務代理等。實驗環境:Eclipse Kepler Release、Intel(R) Core(TM) i5-7200U CPU @ 2.50 GHz 2.71 GHz處理器,4 GB內存。實驗環境的配置如表6所示。 表6 實驗環境配置 為確保實驗結果的公平性,所有算法的參數設置都相同:種群規模為25,最大迭代次數為2 000,任務數分別設置為40、60、80和100,實驗結果在算法運行100次后取平均值作為最終結果。詳細參數設置如表7所示。 表7 參數設置 任務調度的性能指標由總成本C來衡量,即各子任務在虛擬機上的執行時間Eij與云計算資源中任務的執行成本c的乘積之和。其計算公式為 (15) 為驗證MSPSO在求解云計算任務調度問題中的有效性,分別從適應度值、總成本兩個角度,將所提算法MSPSO與LWPSO[28]、GWOPSO[29]及EEAPSO[30]3種改進粒子群優化算法進行比較。 為測試本文算法在總成本上的優劣,分別將MSPSO與LWPSO、GWOPSO、EEAPSO在任務數為40、60、80、100的條件進行實驗對比,對比結果如圖4所示。可以看出,對于所有測試用例,MSPSO的總成本均遠低于其他3種對比算法。這是因為MSPSO中引入了饑餓游戲搜索算法,通過粒子的“饑餓程度”(它們對尋找最優解的影響)動態選擇位置更新策略,可以提高粒子間信息交互能力,加快粒子收斂速度。同時,引入雙重變異限制策略提高了算法尋優效率,有效降低任務執行時間,實現總成本最小化。當任務數為40時,MSPSO總成本比LWPSO、GWOPSO、EEAPSO低14.4%、15.3%、11.2%。隨著任務數逐漸增多,各算法的總成本差額有所減小,當任務達到100時,MSPSO總成本比LWPSO、GWOPSO、EEAPSO低13.5%、12.8%、10.6%。 圖4 不同算法在不同任務量下的成本比較Fig.4 Cost comparison of different algorithms for different task volumes 此外,綜合考慮最大完成時間最少、任務執行總時間最優兩個目標,將尋找最佳調度方案問題轉化為尋找適應度最小值問題。通過比較MSPSO與其他3種算法在適應度值方面的表現來進一步評價算法性能,在不同任務量下的對比實驗結果如圖5所示。對于所有測試用例,MSPSO的適應度值均遠低于其他對比算法,且隨著迭代次數的增加,MSPSO與其他對比算法的適應度差值逐漸增加,驗證了MSPSO在求解云計算任務調度問題中的有效性。原因在于算法中引入了模擬退火算法,在調度過程中動態更新粒子慣性權重,有效平衡了算法的全局搜索和局部搜索能力,避免粒子在算法后期陷入局部極值。在圖5 (a)中,MSPSO的適應度值分別比LWPSO、GWOPSO、EEAPSO低10.5%、10.6%、7.6%。隨著任務數逐漸增多,各算法間的適應度差值有所減小。在圖5 (d)中,MSPSO的適應度值分別比LWPSO、GWOPSO、EEAPSO低9.9%、8.3%、6.5%。 圖5 不同算法在不同任務量下的適應度值比較Fig.5 Comparison of fitness values of different algorithms under different tasks 綜合以上分析,MSPSO相比其他3種對比算法,在適應度值、總成本兩個方面均表現出明顯優勢,適用于求解云計算任務調度問題。 針對粒子群優化算法在求解云計算任務調度問題中存在的不足,提出一種新的融合模擬退火算法、饑餓游戲搜索和雙重變異限制策略的多策略粒子群優化算法(MSPSO)。模擬退火算法依概率動態更新慣性權重,平衡算法的探索與開發;饑餓游戲搜索算法根據粒子的“饑餓程度”(對尋找最優解的影響)優化粒子位置公式,加快粒子收斂;雙重變異限制策略同時約束粒子位置和速度,避免粒子越界。通過與其他3種粒子群算法進行對比實驗,在求解單模態問題時,MSPSO在適應度平均值、最小值、標準差3個方面能夠獲得更優數量級最優解,在求解多模態和固定維數問題時,MSPSO同樣能獲得更優值。此外,在求解云計算任務調度問題時,在總成本、適應度值最小化兩方面MSPSO均表現出明顯優勢。當任務數為40時,MSPSO總成本比LWPSO、GWOPSO、EEAPSO低14.4%、15.3%、11.2%,這得益于動態的位置更新策略提高了粒子間信息交互能力,加快算法尋優效率,縮短任務執行時間。MSPSO適應度值分別低10.5%、10.6%、7.6%,這表明模擬退火算法在平衡算法探索與開發、避免陷入局部極值的有效性。在其他維度中,MSPSO在適應度值、總成本兩個方面也表現出明顯優勢,驗證了MSPSO在求解云計算任務調度問題中的有效性。 然而,隨著任務數的增加,MSPSO在執行任務總成本方面的優越性有所降低。在未來工作中將考慮在負載均衡、資源利用率等方面進行改進,進一步優化算法性能,使其能夠在大規模任務的場景中也表現出明顯的優勢。4.4 實驗設置

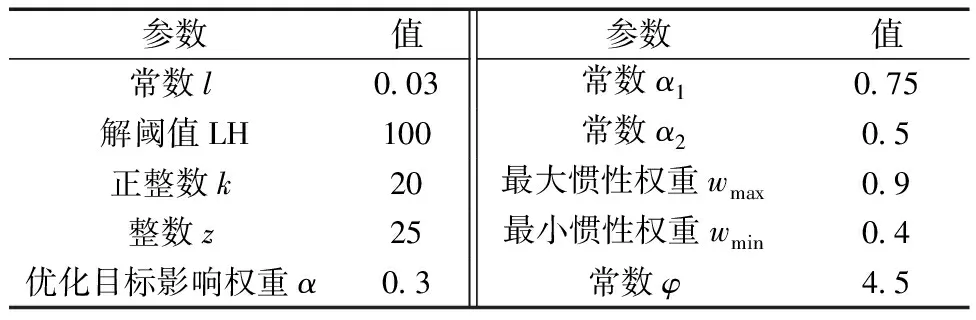
4.5 性能指標
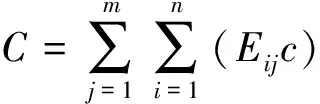
4.6 結果分析
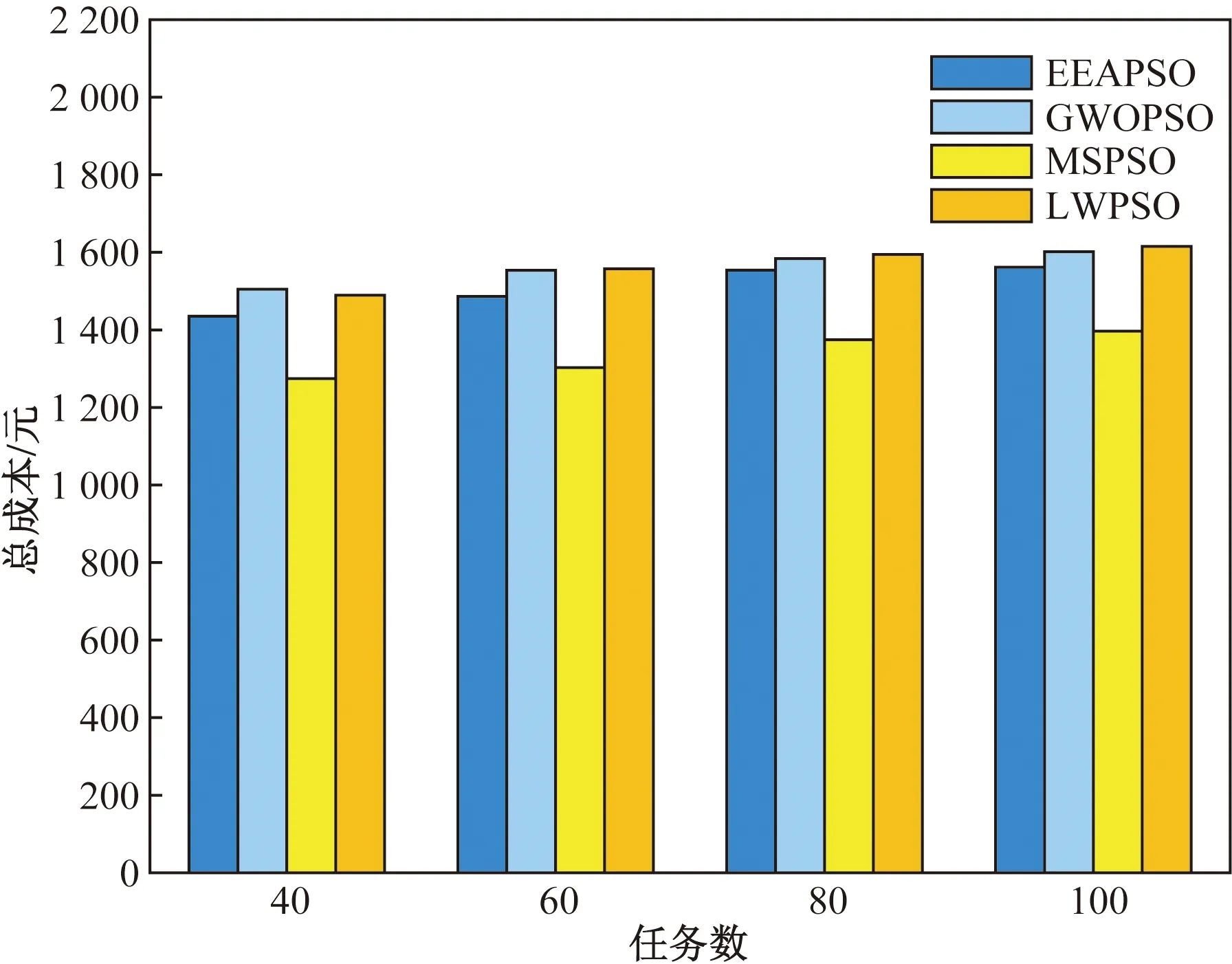
5 結論

