基于高階Lamb 波模態(tài)頻譜差異系數(shù)的腐蝕檢測

陳飛宇 ，盧丙舉 ，曹徐偉 ，曾 亮

（1.中國船舶重工集團公司第七一三研究所，河南 鄭州 450015；2.杭州電子科技大學機械工程學院，浙江 杭州310018；3.西安交通大學機械工程學院，陜西 西安 710049）

航空、船舶、高鐵、能源等領域機械裝備的服役工況多變、服役環(huán)境惡劣，容易誘發(fā)腐蝕，帶來重大安全隱患.以潛艇為例，由于長期工作于壓力高、溫度低、生物污損嚴重的深海海域之中，大量海鹽粒子聚集產生的吸濕潮解現(xiàn)象使金屬表面液膜導電性增強，再加上氯離子的侵蝕作用，其腐蝕行為復雜，破壞程度嚴重.因此，針對這些機械裝備金屬結構的快速腐蝕檢測問題亟待解決.

超聲Lamb 波具有獨特的頻散特性，與層析技術結合可以快速檢測和評估大型薄壁結構中出現(xiàn)的腐蝕損傷[1-2].Malyarenko 等[3-4]利用S0 模態(tài)的飛行時間（time of flight, ToF）作為層析參數(shù)，結合雙跨孔掃查和同步迭代重構技術，實現(xiàn)了平底孔、厚度漸變孔等損傷的評估.Belanger 等[5-6]結合有限元仿真和實驗研究，證明利用低頻基礎模態(tài)檢測腐蝕損傷必須滿足射線理論條件，即損傷特征尺寸需大于Lamb波波長和Fresnel 區(qū)寬度.Huthwaite[7]分析了利用低頻A0 模態(tài)ToF 會欠估計壁厚損失，而利用低頻S0模態(tài)ToF 會過估計壁厚損失的原因.Rao 等[8-9]提出全波反演算法，通過局部優(yōu)化不同頻率下的理論模型與測試數(shù)據之間的波形失配函數(shù)，獲得了可以表征結構剩余厚度的波速圖.通常而言，Lamb 波檢測腐蝕損傷的靈敏度取決于工作模態(tài)在特定頻率范圍內的頻散程度.然而，由于腐蝕區(qū)域相對于待測結構往往比較小，ToF 變化并不顯著，反演結果極易受到路徑長度誤差等的干擾.

多模態(tài)特性是Lamb 波傳播的另一典型特點，可為其損傷檢測提供更為豐富的信息支撐和參數(shù)選擇.Rose 等[10]對比結構中有、無腐蝕損傷情況下高階模態(tài)接收信號的波形差異，并利用高階模態(tài)的截止特性估計腐蝕深度.Luo 等[11]利用脈沖激光器激發(fā)多個Lamb 波模態(tài)，并利用高階模態(tài)和基礎模態(tài)的組合實現(xiàn)微小腐蝕的有效檢測.Cao 等[12]建立包絡差異系數(shù)，度量A1 模態(tài)直達波經過腐蝕損傷后的波形畸變，實現(xiàn)了腐蝕的檢測和定位.

本文利用略高于截止頻率的A1 模態(tài)進行腐蝕檢測，通過建立頻譜差異系數(shù)指標描述損傷對直達波包的散射和模態(tài)轉換效應.隨后，利用有限元分析論證了該指標對不同寬度、深度腐蝕的敏感性和有效性.進一步，針對鋁板中的腐蝕損傷開展實驗研究，實現(xiàn)了損傷的準確成像和精確定位.

1 基于截止特性的腐蝕檢測方法

1.1 高階模態(tài)截止特性

圖1 給出了鋁板中的Lamb 波頻散曲線.材料參數(shù)如下：彈性模量E= 71 GPa，泊松比ν= 0.33，密度ρ= 2 700 kg/m3.圖中：A0、S0 為基礎傳播模態(tài)；A1、S1、S2 為高階傳播模態(tài)；pcutoff,A1和pzgv分別為A1 模態(tài)的截止頻厚積和S1 等模態(tài)的零群速度頻厚積；紅色為對稱模態(tài)，藍色為反對稱模態(tài).

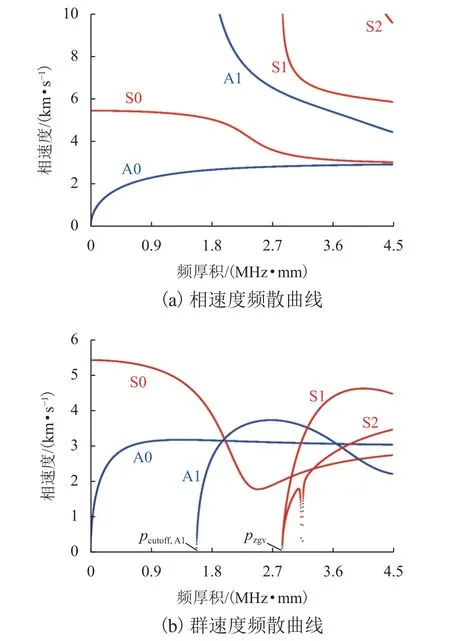
圖1 Lamb 波在鋁板中的頻散曲線Fig.1 Dispersion curves for Lamb waves in aluminum plate

觀察頻散曲線可以發(fā)現(xiàn)，基礎傳播模態(tài)A0 和S0 在所有頻厚積下都會出現(xiàn)，而高階傳播模態(tài)，如A1、S1 和S2 等，只有在特定頻厚積以上才會出現(xiàn).若頻厚積低于截止值，高階傳播模態(tài)可能轉換為非傳播模態(tài)（波數(shù)為虛數(shù)），即只在局部產生振動，無法沿板平面向外傳播能量.高階模態(tài)的對稱模態(tài)截止頻厚積[13]為

對于反對稱模態(tài)，截止頻厚積為

式（1）、（2）中：cL為縱波波速；cT為橫波波速；n為正整數(shù).

對于以高于截止頻率傳播的高階模態(tài)，如果在其傳播路徑上因腐蝕引起的厚度損失足夠顯著，則其對應的頻厚積可能會低于其截止值.高階模態(tài)的部分能量將轉換為其他低階模態(tài)，其余部分能量由于厚度損失而被反射.因此，在截止頻率附近激發(fā)所需的高階模態(tài)，觀察信號的波形或者幅值變化，理論上可實現(xiàn)厚度損失類（如腐蝕、磨損等）損傷檢測.

1.2 直達波相干系數(shù)

對于Lamb 波，腐蝕的出現(xiàn)等效于厚度損失，如果傳播路徑上厚度損失足夠大，頻厚積會減小到截止值以下.靠近截止頻率的高階模態(tài)遇到厚度損失，往往會發(fā)生較其他頻率處更為顯著的模態(tài)轉換現(xiàn)象，一部分能量透射繼續(xù)向前傳播，另一部分能量被反射.因此，在截止頻厚積附近激發(fā)所需的高階模態(tài)并評估其直達波頻域分布的變化，可以有效檢測表面腐蝕.

圖2 給出了A1 模態(tài)群速度頻散曲線隨板厚d變化的演化關系，背景是漢寧窗調制的20 個周期正弦波信號頻譜，中心頻率為1 000 kHz.板厚d從1.8 mm 逐漸減小至1.4 mm，相應地，截止頻率（群速度為0）逐漸增加.當板厚小于1.6 mm 時，A1 模態(tài)的頻帶顯著損失；當板厚減小到1.4 mm 以下時，A1 模態(tài)從激勵頻帶[900, 1 100] kHz 上完全消失.因此，直達波包的改變可以有效預測腐蝕的存在.

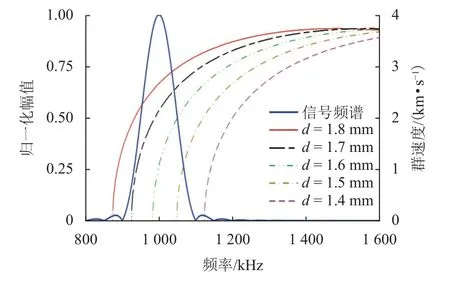
圖2 A1 模態(tài)群速度頻散隨板厚變化的演化關系Fig.2 Evolution of group velocity dispersion of A1 mode with plate thickness

然而，靠近截止頻率處高階模態(tài)的頻散現(xiàn)象非常嚴重，導致直達波在時域的能量擴散，難以直接評估波形畸變的程度.因此，采用頻散補償來提升直達波在時域的能量聚集程度.以中心頻率為ω0的窄帶時域信號f(t)作為輸入，僅考慮頻散關系為k(ω)的單一模態(tài)，其傳播距離為L時得到接收信號g(t)如式（3）；f(t)、g(t)的頻譜F(ω)、G(ω)分別如式（4）、（5）.

式中：A(ω)為整個系統(tǒng)的幅值頻響函數(shù)，包括激勵換能器、接收換能器的幅頻特性以及Lamb 波在介質中傳播的衰減特性等[14]；t為時間；ω為頻率.

在激勵頻帶內進行線性映射可以移除頻散效應、壓縮波包，使得接收信號更容易解釋.在中心頻率ω0處利用一階泰勒展開klin(ω)=k0+k1(ω-ω0)代替實際頻散關系k(ω)，得到補償信號gc(t)及其頻譜Gc(ω)，如式（6）、（7）.

式中：k0和k1由Lamb 波模態(tài)的相速度cp(ω0) 和群速度cg(ω0) 進行定義，分別如式（8）、（9）所示.

以A1 模態(tài)為例，圖3 給出了1 000 kHz 附近表征角波數(shù)與頻率關系的頻散曲線及其一階泰勒展開.采用線性映射方法，可以對頻散的接收信號進行補償，便于從時域中提取關注的模態(tài)成分.

圖3 1.8 mm 鋁板中A1 模態(tài)的頻散關系及其一階泰勒展開Fig.3 Dispersion relationship and first-order Taylor expansion of A1 mode in aluminum plate with a thickness of 1.8 mm

相干函數(shù)通常用于描述在頻域內輸出信號中輸入信號產生輸出信號所占的比例.若輸出信號完全由輸入信號引起（線性系統(tǒng)），則相干函數(shù)等于1，即完全相干.若相干函數(shù)在0～1，則表明有以下3 種可能：有外界噪聲干擾，有其他輸入來源，系統(tǒng)非線性.為了描述厚度損失對直達波包的影響，定義f(t)和gc(t) 的相關系數(shù)為

式中：Sfg(ω)為f(t)和gc(t)的互功率譜密度；Sff(ω)和Sgg(ω)分別為f(t)和gc(t)的自功率譜密度.

相干系數(shù)γfg(ω) 是頻率的函數(shù)，在頻域內描述f(t)和gc(t)的相關性.在此基礎上，損傷因子即頻譜差異系數(shù)可定義為

式中：ωmax和ωmin分別為輸入信號f(t)的頻率上限和下限；B=ωmax-ωmin為輸入信號f(t)的有效帶寬.

靠近截止頻率的A1 模態(tài)成分在厚度損失處發(fā)生顯著的模態(tài)轉換，使得式（4）不再成立，相干系數(shù)γfg下降，得到較大的FSDC 值；反之，若A1 模態(tài)成分改變較小，信號近似完全相干，F(xiàn)SDC 值接近0.損傷因子FSDC 在0～1，其大小可以表征腐蝕損傷情況.

2 有限元分析

為了驗證所提指標的有效性，利用ABAQUS/Explicit 軟件仿真Lamb 波在鋁板中的傳播，該鋁板的寬度為500 mm，厚度為1.8 mm.圖4 給出了包含矩形槽的二維有限元模型，并在板厚度方向建立坐標系，其原點位于模型左邊界厚度方向中點處.圖4中左邊“ × ”表示信號波形在厚度方向各節(jié)點處加載時會被該處節(jié)點的振型幅值所調制.在板的上表面刪除部分單元，得到具有不同寬度、深度的矩形槽，以代表腐蝕.根據已有理論[15]，Lamb 波模態(tài)彼此正交，只有當邊界條件改變時，一種模態(tài)的能量才會轉移到另一種模態(tài).如果將某一模態(tài)的振型施加在厚度方向上，理論上，板中只會產生該模態(tài).激勵信號選擇Hanning 窗調制的周期數(shù)為20 的正弦信號，中心頻率為1 000 kHz，借助中心模態(tài)技術[16]，按照1 000 kHz 的A1 模態(tài)振型（如圖4 左下角所示）在板左邊界的厚度方向上各單元節(jié)點處施加該信號，以生成主導的A1 模態(tài)，與實驗中的情況基本相同.由于激勵頻帶內的模態(tài)振型隨頻率略有變化，因此，結構中仍會存在少量的A0 和S0 模態(tài).仿真中選用四節(jié)點平面應變四邊形單元，在x和z方向上單元尺寸均為0.2 mm.時間步長為5 ns，以捕獲接近A1 模態(tài)截止頻率的Lamb 波響應信號.在距板左邊界300 mm 處的上表面節(jié)點獲取響應位移信號，以避免邊界反射成分.矩形槽的深度取0.2、0.4、0.6 mm，寬度從6 mm 逐漸增加到36 mm，步長為6 mm.對每一種寬度、深度的組合進行時域仿真.記錄上述一系列仿真中測點位置的響應信號，并根據式（11）計算所有情況下的FSDC 值.如圖5所示，當槽深為0.2 mm 時，F(xiàn)SDC 值隨槽寬近似單調遞增.此時，A1 模態(tài)的低頻部分被矩形槽阻擋，高頻部分仍然可以穿過矩形槽，導致相干系數(shù)和FSDC值改變.槽寬越大，A1 模態(tài)發(fā)生的轉換越顯著.然而，當槽深達到0.4 mm 時，A1 模態(tài)在激勵頻帶內幾乎完全消失，如1.2 節(jié)所述.在測點位置接收到的信號是模態(tài)轉換和殘留基礎模態(tài)疊加的結果.盡管FSDC 隨槽寬、槽深之間的變化規(guī)律難以定量描述，但在上述情況下均能得到相對較大的FSDC 值，從而確保了腐蝕的可檢測性.

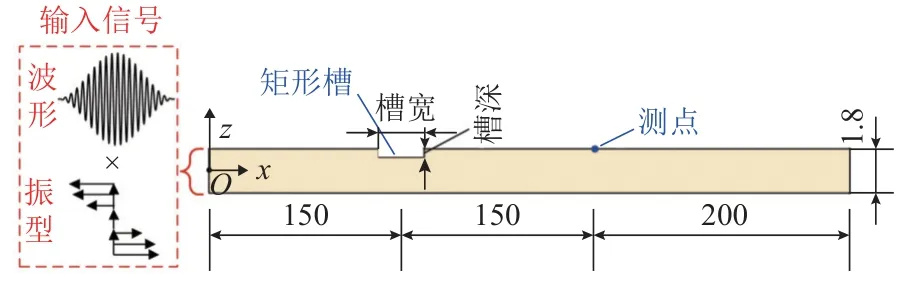
圖4 包含矩形槽的二維有限元模型（左邊界施加1 000 kHz A1 模態(tài)的振型）Fig.4 Two-dimensional finite element model with a rectangular notch (applying A1 mode of 1 000 kHz to the left boundary)

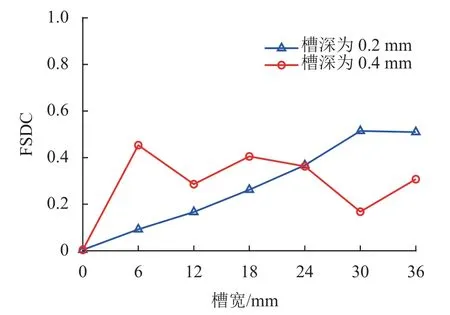
圖5 FSDC 隨矩形槽寬度、深度的演化關系Fig.5 Evolution of FSDC with width and depth of rectangular notch

3 實驗驗證

在500 mm × 500 mm × 1.8 mm 的鋁板上開展實驗，驗證基于A1 模態(tài)截止特性的腐蝕檢測及成像效果.采用Innolas Spitlight 600-10 Nd: YAG 激光器激發(fā)寬帶Lamb 波信號，Olympus C133-RM 超聲探頭接收響應信號，結合帶通濾波，從寬帶響應中提取窄帶響應信號.借助鋁板上下表面環(huán)形磁鐵對的吸引，探頭可以很好地通過甘油與鋁板表面耦合，如圖6 所示.Tektronix DPO-5054B 示波器用于記錄探頭接收到的響應，采樣頻率20 MHz，數(shù)據長度20 000個點.

圖6 激光-超聲系統(tǒng)實驗設置Fig.6 Experimental setup for laser-ultrasonic system

在檢測區(qū)域的板平面建立xOy平面直角坐標系，其中，坐標原點位于試件的中心，試件的實際邊界距離檢測區(qū)域邊界100 mm.在試件上表面人工打磨出一個直徑40 mm 的圓形凹坑區(qū)域，模擬腐蝕損傷.該區(qū)域的中心位于（0, 80 mm）處，最大深度為0.5 mm （位于區(qū)域中心），遠離中心深度逐漸減小，最小剩余厚度為1.3 mm，相當于28%的厚度損失.如第2 節(jié)中所預測的，腐蝕深度越大，腐蝕被檢測到的概率越高.

Lamb 波測試的掃查示意如圖7 所示，圖中：腐蝕區(qū)域以實心圓表示，藍色線條為3 條典型的Lamb波傳播路徑；以L 開頭的點表示激光光斑（激勵點）的位置，而以P 開頭的點表示探頭（接收點）的位置.為了在重構效果與掃查時間之間實現(xiàn)折中，每邊布置15 個激勵/接收點，以完成損傷定位和成像的目的.換言之，有30 個點可作為激勵點，另外30 個點可作為接收點.激勵點位置掃查通過計算機控制兩個步進電機帶動平板在x和y兩個正交方向上移動實現(xiàn)，接收點位置掃查通過手動移動探頭實現(xiàn)，共記錄450 個掃查波形.

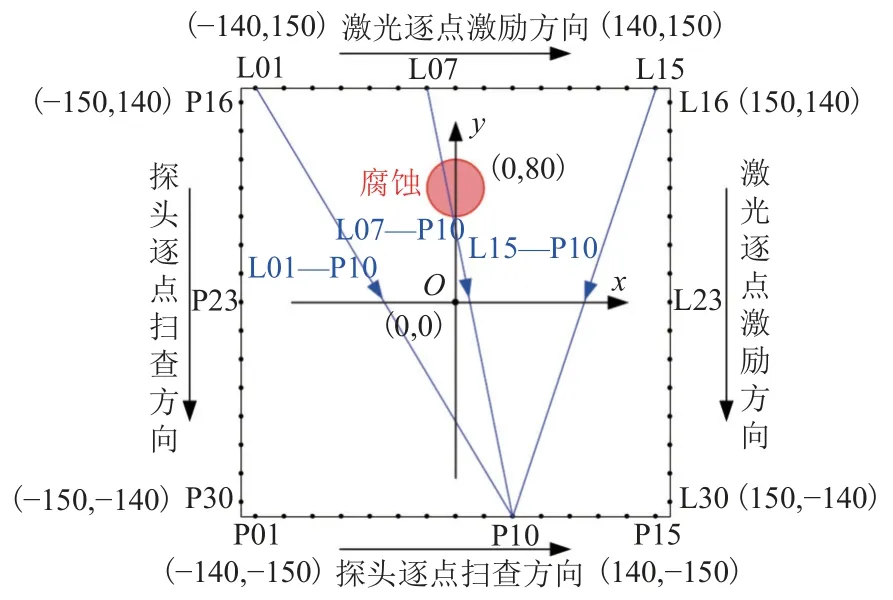
圖7 1.8 mm 鋁板的掃查示意Fig.7 Layout of inspected aluminum plate with a thickness of 1.8 mm

3.1 頻散補償

假設激光器產生的輸入信號是理想的單位脈沖函數(shù)，則原始采集信號h(t)可以被視為系統(tǒng)的單位脈沖響應，其傅里葉變換H(ω)是測試系統(tǒng)的傳遞函數(shù)，包括儀器、激勵、接收以及激勵與接收之間的頻散傳播.通常情況下，整個測試系統(tǒng)可以認為是線性系統(tǒng)，因此，提取的接收信號g(t)[17]為

如第2 節(jié)所述，將Hanning 窗調制的20 個周期正弦信號作為窄帶輸入信號，該信號的中心頻率為1 000 kHz，帶寬為[900, 1 100] kHz，略高于Al 模態(tài)的截止頻率（878 kHz）.以路徑L15—P10 為例（如圖7 所示），激光光斑在L15（140 mm, 150 mm）處，而探頭在P10（40 mm, -150 mm）處，名義傳播距離為316.2 mm.圖8（a）給出了路徑L15—P10 提取的窄帶響應信號.由于多個頻散成分相互疊加，波形非常復雜，難以從時域提取所需的成分.為了反映其時頻能量分布，圖8（b）給出了該路徑響應信號的短時傅里葉變換（25 μs 的高斯窗）時頻譜圖，以及計算得到的群延遲曲線（名義傳播距離316.2 mm 除以理論群速度），A1 模態(tài)在1 000 kHz 左右能量占主導，并且該模態(tài)的理論波達時間與時頻能量峰值基本重合，從而保證了A1 模態(tài)在截止頻率附近足夠的檢測靈敏度.隨后，對A1 模態(tài)進行頻散補償，結果如圖8（c）所示，其中第1 個波包可以清楚地識別為直達A1 模態(tài).

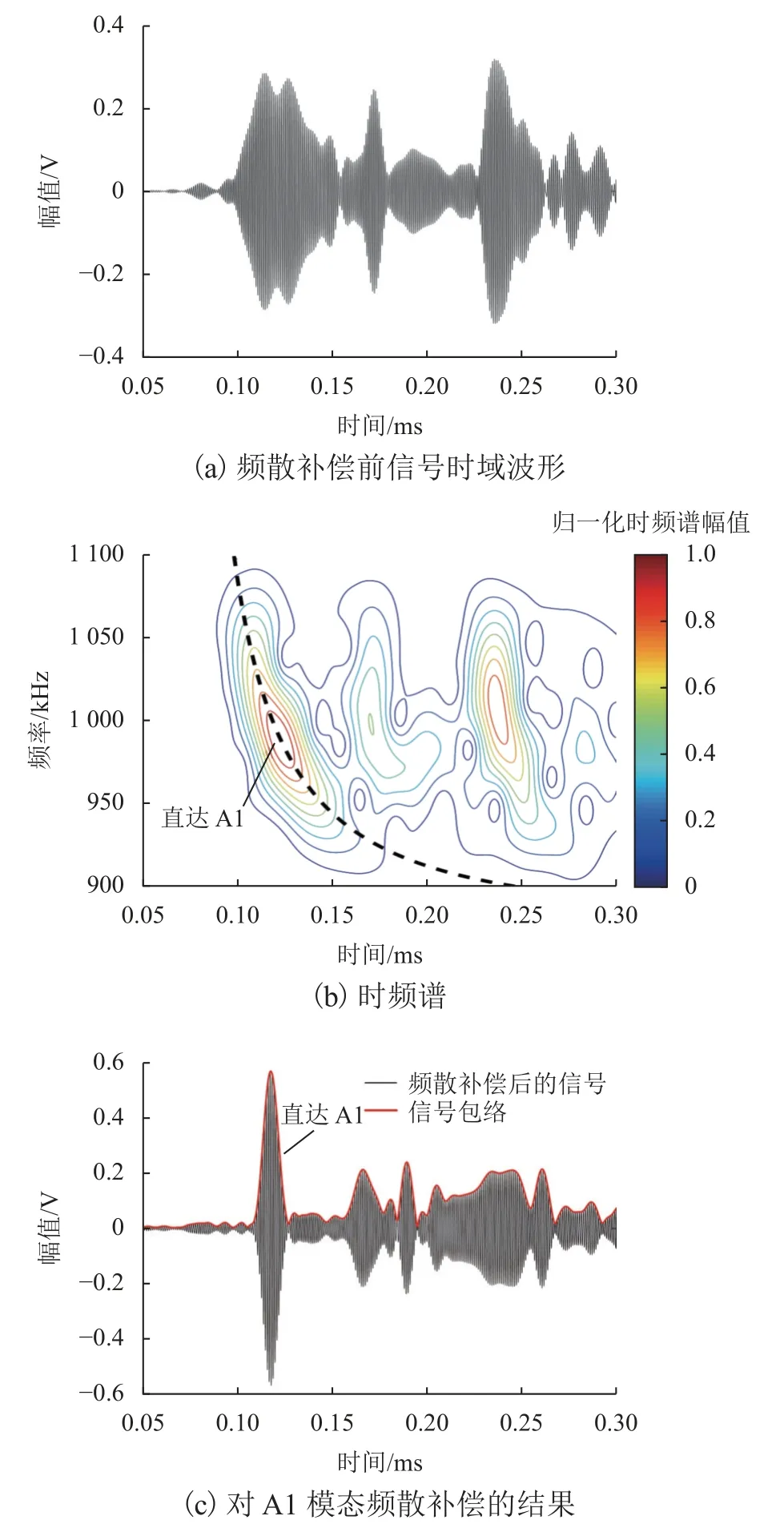
圖8 健康路徑L15—P10 提取的窄帶響應信號Fig.8 Extracted narrow-band response signal from intact path L15—P10

3.2 FSDC 計算

步驟1提取A1 模態(tài)的窄帶響應信號，其頻帶略高于A1 模態(tài)的截止頻率；

步驟2通過線性映射方法對A1 模態(tài)進行頻散補償；

步驟3乘以合適的窗函數(shù)（以傳播時間為中心），得到直達A1 模態(tài)；

步驟4計算補償后的直達 A1 模態(tài)和輸入信號的相干系數(shù)，進一步求得 FSDC.

健康路徑L15—P10 的補償信號如圖9（a）所示.通過乘以合適的窗函數(shù)，可以濾除噪聲，同時選擇性地保留直達A1 模態(tài)，這是因為補償后的直達A1 模態(tài)具有較好的時域聚集性.基礎模態(tài)A0和S0 的干擾雖然無法完全排除，但其能量很弱，對結果影響較小.圖中，虛線為經第i條路徑的直達波以傳播時間Ti為中心的Tukey 窗函數(shù)w（t），如式（13）.

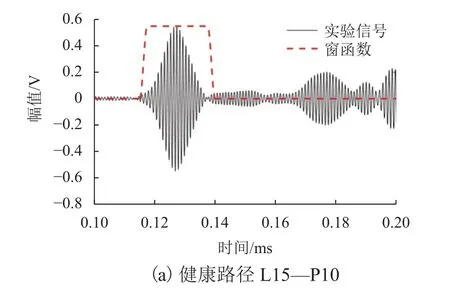
圖9 健康、損傷路徑的補償實驗信號Fig.9 Compensated experimental signals of intact and damaged paths

式中：ΔT為總窗長，取25 μs，可以包含補償后的直達A1 模態(tài)；α為下降段占總窗長的比值，取0.2；Ti=130.2 μs，即按照名義傳播距離除以1 000 kHz 時A1 模態(tài)的群速度，再加上輸入信號持續(xù)時間20 μs的一半計算.

窗函數(shù)在20 μs 時間范圍內為1，在此區(qū)域外，窗函數(shù)在5 μs 時間范圍內按正弦規(guī)律從1 逐漸下降至0.通過乘以該窗函數(shù)，可以從補償信號中有效提取所需的直達A1 模態(tài).對于遠離腐蝕的健康路徑L15—P10，所選窗內的FSDC 值為0.029 3.由于該值接近0，因此,可以判斷該路徑上沒有腐蝕，為健康路徑.

圖9（b）給出了穿過腐蝕的損傷路徑L07—P10 補償信號.路徑L07—P10 的傳播時間計算為126.3 μs.如果激光光斑和探頭之間的路徑不穿過腐蝕，則窗函數(shù)內的波形應包含直達A1 模態(tài).然而，實際并未觀察到直達A1 模態(tài)，可以歸因于厚度損失引起的強烈模態(tài)轉換以及散射.圖9(c)給出了健康路徑L01—P10 的補償信號，其中部分散射波包與直達波包發(fā)生了疊加.該路徑的FSDC 值為0.131 9，介于健康路徑與損傷路徑之間.損傷路徑L07—P10 的FSDC 值為0.456 1，遠大于健康路徑L15—P10 的FSDC 值0.029 3，與先前的假設一致，表明了腐蝕的存在.

3.3 基于FSDC 的概率成像

圖10 給出了所有450 條路徑的FSDC 值，其中超過80%（367 條）的路徑FSDC 小于0.100 0，僅有幾條路徑FSDC 值較大，即為損傷路徑.

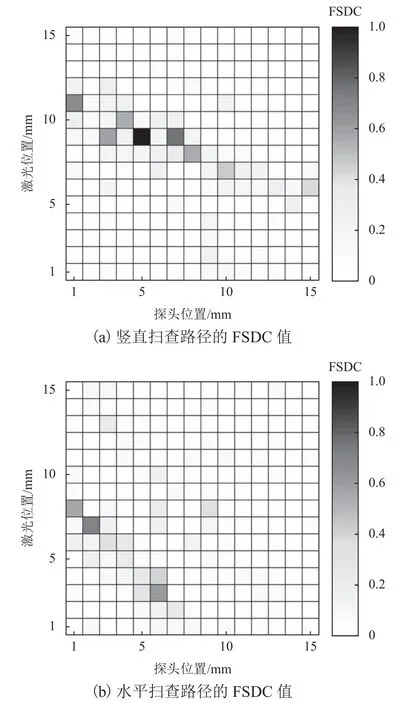
圖10 實驗中所有路徑的FSDC 值Fig.10 FSDC values for all paths in experiment

隨后，檢測區(qū)域被離散成均勻的像素點，所有路徑均為連接激勵、接收點的直線，則在第j個像素點處發(fā)生腐蝕的概率為

式中：N為路徑總數(shù)；σ為標準差，取0.01；dij為從第j個像素點到第i條路徑的距離；λi為第i條路徑的損傷因子FSDC 值；式（14）中方括號內的項是概率成像算法中常用的概率密度函數(shù)[18].

Pj的值越大，表示該像素點處發(fā)生腐蝕的可能性越大.

將所有高斯分布函數(shù)加權的FSDC 相加，得到整個檢測區(qū)域的概率成像結果，如圖11 所示.圖中，虛線圓為實際腐蝕區(qū)域邊界，十字為最大值像素點.該成像結果以像素圖的形式，覆蓋300 mm × 300 mm的檢測區(qū)域，每個像素點代表試件中邊長為2 mm的正方形區(qū)域.可以觀察到，圖像中重構的異常區(qū)域與實際腐蝕具有較高的重合度，證明了方法的有效性和準確性.另一方面，由于更多的路徑穿過腐蝕的下半部分，導致最大像素點 （2 mm, 68 mm）偏離實際腐蝕中心 （0, 80 mm）約12.2 mm.

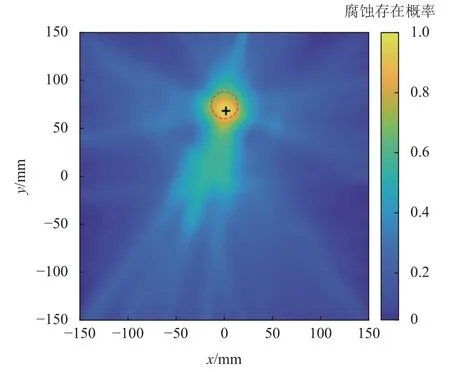
圖11 基于FSDC 的概率成像結果Fig.11 Image obtained from probability reconstruction based on FSDC

3.4 與傳統(tǒng)層析成像方法對比

為了凸顯所提方法的優(yōu)勢，將其與基于波包飛行時間的Lamb 波層析成像方法進行對比.由于800 kHz 附近的S0 模態(tài)能量足夠高，群速度在幾個模態(tài)中最大，且頻散足夠嚴重，因此，選擇其作為對比實驗的工作點.

將漢明窗調制的20 個周期數(shù)的正弦信號作為窄帶輸入信號，中心頻率為800 kHz，根據式（12）從寬帶響應信號中提取窄帶響應信號.其中，ToF 取直達S0 波包的包絡峰值所對應的時刻.采用同步迭代重構技術（simultaneous iterative reconstruction technique，SIRT）重構腐蝕區(qū)域.每次迭代中，首先計算所有射線的更新值，然后，同時更新所有像素點的慢度值[19-20].圖12 給出了基于ToF 的SIRT 重構結果，即慢度（速度倒數(shù)）圖.

圖12 基于ToF 的層析成像Fig.12 ToF-based tomographic image

對于800 kHz 附近的S0 模態(tài)，厚度損失導致該區(qū)域的S0 模態(tài)群速度增大，慢度值減小.然而，在重構的慢度圖中，幾乎無法觀察到腐蝕區(qū)域.對于該結果，可以從以下方面進行解釋：1） 在實驗中，探頭和激光光斑的尺寸不可忽略，因而難以準確估計傳播路徑的長度；2） 厚度損失導致的ToF 變化量通常很小，使得重構結果受傳播路徑長度誤差的影響更大.總體而言，本文提出的方法對厚度損傷具有較高的靈敏度，能夠抗拒路徑長度誤差等因素的干擾，實現(xiàn)腐蝕損傷的準確定位.

4 結 論

1） 本文根據靠近截止頻率的高階Lamb 波模態(tài)對厚度損失的高敏感性，提出了表征腐蝕損傷的FSDC指標.在結構健康狀態(tài)下，補償信號與輸入信號完全相干，F(xiàn)SDC 為0；腐蝕損傷發(fā)生后，截止頻率附近的高階模態(tài)發(fā)生散射或模態(tài)轉換，相干系數(shù)顯著下降，產生較大的FSDC 值.

2） 利用有限元仿真分析了FSDC 隨槽寬、槽深之間的變化規(guī)律，驗證了FSDC 對腐蝕損傷檢測的敏感性和有效性.

3） 將FSDC 指標與概率成像算法結合，實現(xiàn)了腐蝕損傷的準確定位.通過與傳統(tǒng)層析成像方法的結果對比可以發(fā)現(xiàn)，本文所提方法比傳統(tǒng)層析具備更好的腐蝕檢測靈敏度和抗干擾能力.