啞鈴型橋梁結構畸形波浪力水槽試驗及簡化算法

康啊真 ，顧宇航 ，張東明 ，金 可 ，祝 兵 ，楊 兵

（1.西南交通大學土木工程學院，四川 成都 610031；2.成都大學建筑與土木工程學院，四川 成都 610106）

跨海橋梁基礎施工時可能面臨風大、浪高等惡劣海況，如在建的平潭海峽公鐵兩用大橋自2013 年開建以來，2014 年、2015 年、2016 年分別經歷了6、7、6 次臺風，100 年一遇最大浪高9.69 m[1].為了有效減小波浪荷載，近年來一種新型啞鈴型橋梁結構廣泛應用于跨海橋梁海上基礎施工和設計中[2].

已有一些學者針對新型啞鈴型結構的波浪力作用問題進行研究.黃宇[3]采用有限元軟件對復雜海況下啞鈴型承臺鋼吊箱圍堰的受力進行了驗算，保證了施工安全，并為相同類型鋼吊箱圍堰設計與施工提供參考.劉勇等[4]采用試驗與數值方法研究了啞鈴型圍堰在水流作用下的受力特點，研究并分析了其在不同流速、吃水深度、水流夾角下的水流力作用.黃博等[5]建立了波浪與啞鈴型結構的相互作用模型，并模擬了三維波浪作用下啞鈴型結構下放過程中的受力情況.Kang 等[6-7]采用試驗與數值方法研究了啞鈴型結構與波浪（流）之間的相互作用，分析了啞鈴型結構的水動力系數，對結構周圍的流動模式，包括自由液面三維渦度分布進行了數值分析.上述研究中大多僅從規則中波角度考慮（如線性波、stokes波等），而畸形波或隨機波模擬極端波浪可能更具有代表性[8].Chien 等[9]分析了海上畸形波的出現概率，并指出臺風過后畸形波的發生概率顯著增加.

目前，關于結構與畸形波相互作用的研究主要關注垂直或水平圓形結構，比如大型海洋結構TLP（tension leg platform）、Spar 型海上發電平臺、浮式結構在畸形波作用下的水動力問題等.畸形波與圓柱相互作用的影響規律及簡化算法不一定適用于啞鈴型跨海橋梁結構.康啊真等[10]開展了跨海橋梁啞鈴型圍堰畸形波波浪力試驗研究，研究了圍堰吃水深度、畸形波最大波幅、入射角度對結構周圍的波面位移及其所受波浪力的影響.但上述研究中并未考慮譜峰頻率、頻率范圍、聚焦位置等參數影響、也沒有對啞鈴型橋梁圍堰的畸形波浪力簡化算法進行研究.

本文在文獻[10]的基礎上，基于波浪水槽試驗進一步研究了入射波譜的譜峰頻率、頻率范圍、聚焦位置等參數對啞鈴型橋梁結構周圍波面爬高及其所受波浪力的影響，并基于繞射理論提出畸形波作用下啞鈴型橋梁結構波浪力譜的簡化算法.

1 試驗設置

1.1 試驗設備與模型設計

本試驗于西南交通大學深水大跨橋梁試驗中心的中型波流試驗水槽中進行，水槽長60.0 m，寬2 m，高1.8 m.試驗時水槽一側設有用于產生波浪的推板造波機，另一側設有用于減小波浪反射的消波灘，試驗詳細布局見圖1.所選取的啞鈴型橋梁結構原型尺寸長33.9 m，寬15 m，高30.0 m.基于平潭海峽公鐵兩用大橋橋址區海域水深條件、主墩圍堰尺度，且綜合考慮試驗水槽的條件，選取橋梁結構固定吃水12.0 m，水深48.0 m.試驗模型依據Froude 相似準則按1∶60 （模型/原型）的比例設計.模型及高程尺寸均控制在1.0 mm 以下，試驗中模型完全密封，并忽略其他附屬結構.圖1（c）展示了啞鈴型橋梁結構模型的詳細尺寸.

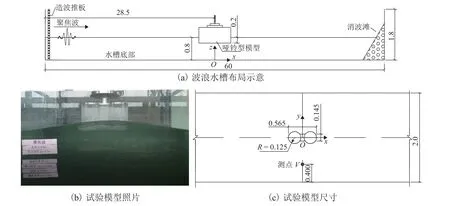
圖1 波浪水槽布局圖（單位：m）Fig.1 Layout of the wave flume (unit：m)

試驗通過采樣頻率200 Hz，量程475 N 的Omega85 六軸力/力矩測力天平傳感器測量啞鈴型結構畸形波浪力作用，試驗模型與測力天平傳感器剛性連接并放置在距離造波機28.5 m 處.采用頻率100 Hz，精度0.1 mm 的無線數字波高儀測量波面變化.未放結構物前，首先將波高儀布置在模型位置的中心線上進行波場率定.當放置結構物后，為了保障模型固定連接裝置的操作空間，只能將波高儀置于偏離模型中點位置的點V處，用于測量波浪與結構物相互作用之后的波面時程，具體位置見圖1（c）.其中，波面和波浪力數據采樣時長均為100 s

1.2 試驗參數

試驗中模型吃水為0.2 m，水深為0.8 m.測量了2 種類型波浪：畸形波與規則線性波.本次試驗采用改進的JONSWAP 譜產生畸形波.考慮到最大波幅的影響，在頻率范圍0.5～1.2 Hz，譜峰頻率0.8 Hz，聚焦位置28.5 m 情況下最大波幅分別取0.04、0.06、0.08、0.10 m.考慮到頻率范圍的影響，在最大波幅0.06 m，譜峰頻率0.8 Hz，聚焦位置28.5 m 情況下頻率范圍分別取0.6～1.1、0.6～1.2 與0.5～1.3 Hz.考慮到譜峰頻率的影響，在最大波幅0.06 m，頻率范圍0.5～1.2 Hz，聚焦位置28.5 m 情況下譜峰頻率分別取0.6、0.7、0.8、0.9、1.0、1.1 Hz.考慮到聚焦位置的影響，在最大波幅分別為0.06、0.08、0.10 m 頻率范圍0.5～1.2 Hz，譜峰頻率0.8 Hz 情況下聚焦位置分別取28.2、28.5、28.8 m.試驗同時測量了規則線性波.在波高0.08 m 情況下周期分別取0.85、1.00、1.10、1.20、1.40、1.60、1.80 s.波高0.12 m 情況下周期分別取1.11、1.25、1.40、1.43、1.60、1.67 s.在周期1.6 s 情況下波高分別取0.08、0.10、0.12、0.14 m.其中，規則線性波波高定義為規則線性波相鄰的波峰和波谷間的垂直距離，周期定義為規則線性波兩相鄰波峰（或波谷）經過同一點所需要的時間.畸形波參數定義見第3.1 節.

1.3 畸形波生成及驗證

Kharif 等[11]提出了在波陡度和頻譜寬度最低階的二維深水波列的簡化非線性模型，基于線性疊加原理，假定波浪在時刻tn聚焦于xn位置處，即各組成波的波峰在時間t=tn，位置x=xn處同時同地出現，則二維聚焦波在任意位置的波面可表示為

式中：Nf為組成諧波總數；ai為各組成波對應波幅（m）；ωi為各組成波的角頻率；Li為各組成波的波長；ki和ωi滿足色散關系，如式（2）.

式中：d為水深.

當確定了聚焦時間和聚焦位置后，聚焦波焦點處的最大波幅An只由各組成波的波幅ai決定，如式（3）.

本文試驗采用諧波波幅譜確定方法即采用不規則波浪譜，波浪譜選用JONSWAP 譜.

本文利用由Goda[12]提出的經改進的JONSWAP譜型生成畸形波，即

式中：Hs為有義波高；ωp為譜峰頻率； γ 為波浪譜譜峰升高因子，一般取3.3；ω為波浪圓頻率；ωm為譜峰圓頻率.

2 參數分析

水深一定時，影響畸形波波浪特性的主要參數為聚焦波幅、譜峰頻率（fp）、頻率范圍（Δf）、聚焦位置（λ）以及頻譜類型.本節側重分析了其他參數一定時譜峰頻率、頻率范圍和聚焦位置對啞鈴型模型放置下測點畸形波波面與波浪力的影響.為了便于比較，圖中一些試驗結果的相位根據需要做了調整.試驗工況如表1 所示.

表1 試驗工況Tab.1 Test conditions

2.1 譜峰頻率影響

為了分析fp對啞鈴型橋梁結構周圍波面位移及其所受波浪力的影響，以下工況固定最大波幅Amax=0.06 m，Δf=0.7 Hz （頻率介于0.5～1.2 Hz）.試驗共測試了fp=0.6，0.7，0.8，0.9，1.0，1.1 Hz 共6 個畸形波工況.圖2（a）給出了其中3 個工況fp=0.6，0.8，1.0 Hz 下測點V處波面位移（ η ）時程曲線.圖中，t為時間.由圖可見，這3 條曲線的峰值與谷值差異較小.圖2（b）繪制了在測點V處的波面位移極值，研究表明，fp對啞鈴型橋梁結構周圍的波面位移影響較小.

圖2 fp 對測點V 波面位移及畸形波波浪力影響Fig.2 Influence of peak frequency fp on wave elevations at point V and freak wave forces

圖2（c）與圖2（d）分別給出了fp=0.6，0.8，1.0 Hz工況下模型順波向波浪力Fx與垂向浮托力Fz時程曲線.而圖2（e）與圖2（f）定量給出了Fx及Fz正、負向峰值隨fp的變化規律.Fx絕對值隨fp增加先增大后減小，但變化幅度較小.而Fz絕對值隨fp增加而減小，且變化明顯.根據畸形波的水動力特性計算研究[13]，畸形波波峰附近動水壓力隨著譜峰頻率的增大而增大，而在靜水面附近以下沿水深的增大會呈現譜峰頻率越大動水壓力數值越小的相反規律.由于本次實驗結構吃水較小，可能由于譜峰頻率的增大會導致結構受到的動水壓力在波峰附近增大而結構底部附近減小，結構上下部分變化的動水壓力相互抵，消導致隨著fp的增大Fx變化幅度較小.而Fz由于本次試驗只與結構底部受到的動水壓力有關，所以可能導致了其絕對值隨譜峰頻率fp增加而減小.

2.2 頻率范圍影響

為了分析Δf對啞鈴型橋梁結構周圍波面位移及其所受波浪力的影響，以下工況固定最大波幅Amax=0.06 m，譜峰頻率fp=0.8 Hz.試驗共測試了Δf=0.5 （頻率介于0.6～1.1 Hz），0.6（頻率介于0.6～1.2 Hz），0.7（頻率介于0.5～1.2 Hz），0.8 Hz （頻率介于0.5～1.3 Hz）共4 個畸形波工況.圖3（a）與圖3（b）分別給出了測點V處波面位移時程曲線與其統計峰值.研究表明，頻率范圍Δf對結構周圍波面位移影響不大.這是由于JONSWAP 頻譜的低頻和高頻部分的波能很小，頻譜兩側頻率的改變對波面位移的影響可以忽略不計.

圖3 Δf 對測點V 波面位移及畸形波波浪力影響Fig.3 Influence of frequency bandwidth Δf on wave elevations at point V and freak wave forces

圖3（c）與圖3（d）分別給出了Δf=0.5，0.6，0.7，0.8 Hz 工況下Fx與Fz的時程曲線.圖3（e）與圖3（f）定量給出了Fx及Fz正、負向峰值隨Δf的變化規律.Δf對Fx和Fz波浪力的影響較小，這是由于在譜峰頻率附近的波能量占比相對較大，而在低頻帶和高頻處的波能量相對較小.因此，當頻率兩側改變時，總波力改變較小.

2.3 聚焦位置影響

為了分析畸形波聚焦位置 λ 對啞鈴型橋梁結構周圍波面位移及其所受波浪力的影響，以下工況固定頻率范圍Δf=0.7 Hz （頻率介于0.5～1.2 Hz），fp=0.8 Hz.試驗共測試了 λ =28.2 （模型迎浪面附近），28.5 （模型形心處），28.8 m （模型背浪面附近）3 個畸形波工況.圖4（a）與圖4（b）分別給出了不同聚焦位置下測點V處波面位移時程曲線與其統計峰值.可以看到，由于模型的存在，測點V處波面位移峰值在當畸形波聚焦位置在模型形心處（28.5 m）時并不是最大.隨聚焦位置數值的增大，測點V處波面位移峰值逐漸增大.

圖4（c）與圖4（d）分別給出了 λ =28.2，28.5，28.8 m工況下Fx與Fz時程曲線.圖4（e）與圖4（f）定量給出了Fx及Fz正、負向峰值隨聚焦位置的變化規律.可以看到，Fx及Fz正向峰值均在當畸形波聚焦位置在模型形心處（28.5 m）時達到最大，這是由于畸形波所有子波的疊加在聚焦位置達到峰值，此時波峰達到最大值，在各子波周期一定的情況下產生的波峰越大結構受到的正向波浪力越大.

3 波浪力譜簡化算法

3.1 理論分析

本節主要探討圓柱波浪力簡化算法是否同樣適用于啞鈴型橋梁結構畸形波浪力譜的計算.首先，參考文獻[14]對畸形波局部波參數進行定義.

對于圓柱波浪力通常用Morison 方程和繞射理論計算.如圖5 [15]所示，海洋結構的波浪力可以分為4 個區域，也給出了2 種波浪力方法的應用范圍.圖5 中：H為波高；L為局部波長；D為墩柱迎浪面的特征長度.Morison 方程與繞射理論分別應用于區域Ⅲ與區域Ⅱ，并且均可應用于區域Ⅰ.圖中垂直線（D/L=0.2）代表繞流影響的閾值，水平線（H/D=1.0）代表黏性影響的閾值[14].具體來說，D/L是散射參數，表達了散射對柱體結構的影響，當D/L低于0.2 時，波浪荷載主要受慣性力影響，D/L越大，繞流影響越明顯.H/D是一個類似Keulegan-Carpenter 數的參數，描述了阻力相對于慣性力的重要性.

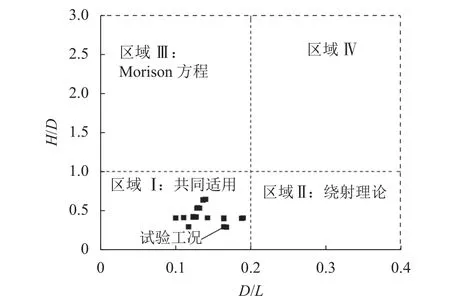
圖5 畸形波計算方法判定[15]Fig.5 Judgment of the freak wave calculation method[15]

基于畸形波局部參數定義，試驗范圍內畸形波計算方法的適用范圍見圖5.本次試驗畸形波數據均在區域Ⅰ（2 種方法均適用）范圍內且在黏性影響范圍外（可不考慮阻力）.以下嘗試采用繞射理論估計啞鈴型橋梁結構畸形波力譜，并將估算結果與試驗結果進行比較.

3.2 基于繞射理論的譜分析方法

Maccamy[16]等提出了一種基于繞射理論的大尺度圓柱波浪力計算方法，表明波浪遇到柱體會產生一個遠離柱體的波浪.入射波與散射波疊加在一起形成一個新的波場.采用微幅波理論，作用在單位高度柱體上的水平波浪力（順波向）表示為

式中：z為沿柱體某一高度（z=0 代表海床底標高）；α為初始相位角(?)；與(?)是第一類與第二類貝塞爾函數的導數； ρ 為水密度.

計算最大波浪總力的方程通常用類似于Morison方程的形式來寫.此時的質量系數CM即為等效質量系數CM1，即

當D/L＜0.2 時，入射波對結構的繞射效應可以忽略，在這種情況下，CM1約等于質量系數CM[17]，此時等效質量系數可按式（10）、（11）計算.

式中：FHLmax為最大總水平慣性力；S為柱體截面積；z1、z2為計算點的垂直高度（m）.

譜分析方法常用于計算不規則波浪作用下的波浪力.根據頻率響應法，墩柱上總波浪力譜的傳遞函數可表示為

式中：由于本次實驗結構迎浪面為圓柱，所以D為圓柱直徑；k為波數；d1為截斷墩柱底部到水床的距離.

3.3 啞鈴型結構畸形波波浪力譜

3.3.1 啞鈴型橋梁結構的傳遞函數

根據式（10）、（11），試驗所得的規則線性波作用下啞鈴型橋梁結構的CM1與D/L的擬合曲線如圖6（a）所示.由于本試驗畸形波D/L系數均小于0.2，式（12）中的等效質量系數近似為質量系數，則啞鈴型橋梁結構的傳遞函數如圖6（b）所示.

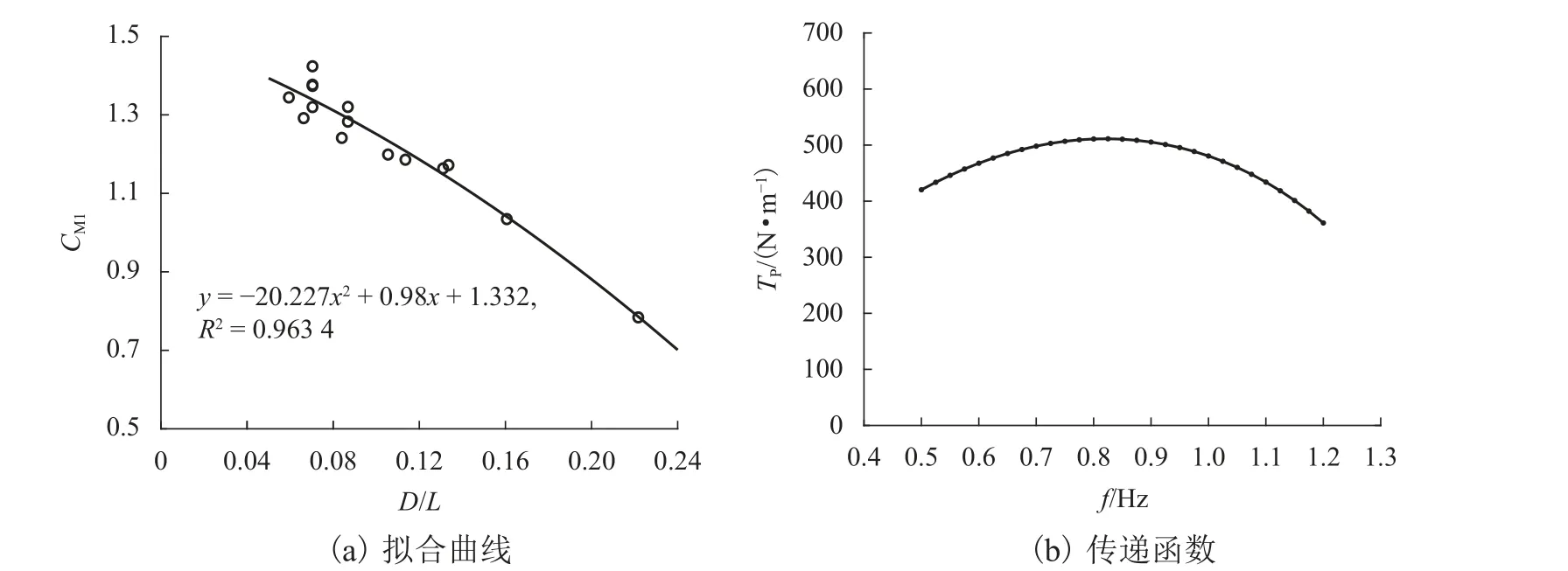
圖6 傳遞函數估算：Fig.6 Estimation of transfer function

3.3.2 畸形波波浪力譜

啞鈴型橋梁結構的畸形波波浪力譜由式（13）給出.

式中：Spp(f) 為波浪力譜；Sηη(f) 為入射波面譜；f為頻率.

已知入射波的波面譜和畸形波的傳遞函數，可以根據式（13）計算出畸形波作用于啞鈴型結構上所產生的波浪力譜.畸形波波浪力譜的估算結果與實測試驗所得波浪力譜對比如圖7（a）所示.計算和實測的畸形波波浪力能量和統計波浪力譜峰值如圖7（b）所示.研究表明計算結果與試驗數據吻合較好，可見3.2 節的繞射理論對啞鈴型橋梁結構畸形波浪力譜的計算具有良好適用性.值得指出的是，由于規則線性波的試驗數據有限，且其相對特征長度D/L較為集中，這導致傳遞函數等效質量系數擬合在部分區域未能正確反映真實情況，因此，部分結果存在一定的偏差.總體而言，該簡化算法可為啞鈴型橋梁結構畸形波波浪力譜的估算提供新的方向.研究結果可為畸形波作用下啞鈴型橋梁結構的疲勞可靠性分析提供波浪力譜模型.

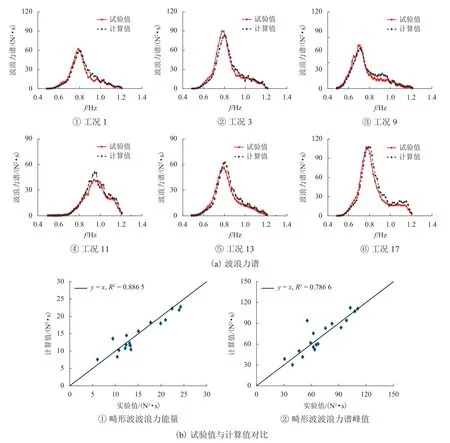
圖7 波浪力譜估算Fig.7 Estimation of wave force spectrum

4 結 論

本文基于波浪水槽試驗研究了譜峰頻率、頻率范圍和聚焦位置對啞鈴型橋梁結構周圍波面位移及其所受波浪力的影響.基于繞射理論，提出了可有效估算畸形波作用下啞鈴型橋梁結構波浪力譜的簡化方法.得出以下幾個結論：

1） 畸形波譜峰頻率對啞鈴型橋梁結構周圍的波面位移及其所受波浪力有一定影響.隨著譜峰頻率的增加，啞鈴型橋梁結構順波向波浪力絕對值隨fp增加先增大后減小，但變化幅度較小，而垂向浮托力絕對值明顯減小.這可能是由于畸形波波峰附近動水壓力隨著譜峰頻率的增大而增大，而在靜水面附近以下沿水深的增大會呈現譜峰頻率越大動水壓力數值越小的相反規律.

2） 聚焦位置對啞鈴型橋梁結構周圍的波面位移及其所受波浪力有重要影響.當畸形波聚焦位置在模型形心處時，波浪力正向峰值達到最大，這是由于畸形波所有子波的疊加在聚焦位置達到峰值，此時波峰達到最大值，在各子波周期一定的情況下產生的波峰越大結構受到的正向波浪力越大.

3） 在本試驗研究中頻率范圍的影響不大.這是由于JONSWAP 頻譜的低頻和高頻部分的波能很小，頻譜兩側頻率的改變對波面位移及啞鈴型橋梁結構所受波浪力的影響可以忽略不計.

4） 由于本試驗畸形波參數位于區域I （D/L<0.2,H/L<1），阻力較小可忽略不計.基于繞射理論可有效估算畸形波作用下啞鈴型橋梁結構的經驗傳遞函數.本研究為啞鈴型橋梁結構波浪力譜的估計提供了一種新的有效方法，研究結果可為畸形波作用下啞鈴型橋梁結構的疲勞可靠性分析奠定力譜模型.值得注意的是，本研究僅考慮了一種固定的啞鈴型橋梁結構尺寸，經驗傳遞函數在不同長寬比啞鈴型結構的適用性有待進一步研究.