地下管線探測三維數據聯合平差模型

張劍峰

(蘭州市勘察測繪研究院,甘肅 蘭州 730030)

0 引 言

城市地下管網是城市生存和發展的生命線,高質量地下管線數據對維系城市日常功能、提升防災救災能力至關重要,各地對地下管線精細化管理和竣工測量工作日益重視。而對已覆土的城市管線實施竣工測量時,由于干擾因素和探測方法限制,數據誤差較大,往往會出現燃氣、熱力、給水、工業等硬管的探測結果和實際形態偏差明顯,如管線轉角、半徑與實際不符,直線上點不共線,圓弧上點不共弧等。在實際應用中,不得不參照轉角、半徑等參數做一些近似性強制歸化工作,導致成果精度較低,而且由于只考慮水平方向的約束,而忽略豎向分量,致使管線在三維框架下仍存在轉角和半徑失真,同一直線的豎向坡度不一致等情況。

由于以往管線探測項目以常規普查為主,主要目標是解決資料有無問題,加上歷史資料較少,普查成果龐雜,對管線固有屬性表達的精準性需求并不嚴格。但目前,管線測量工作的重心逐步轉向竣工測量和已有成果質量的提升,各種失真情況會直接影響對設計、施工、測驗等各環節的質量評價和績效考核,原有作業模式嚴重影響了成果質量。目前,尚無面向三維框架的管線探測數據平差方案以供探測工作者使用,甚至相關研究也比較少。

文獻[1]基于管線設計資料,通過計算管網水平和豎向閉合差以及相鄰邊形成面片閉合差的方法,對管線空間數據進行平差處理,但對探測數據的質量檢測和優化并沒有涉及。文獻[2]基于管線屬性邏輯、拓撲關系、空間碰撞等提出了通過建立管線檢查知識規則庫及其推理機,利用GIS對管線數據進行智能化檢查的理論與方法。文獻[3-6]研究管線可視化以及對管線數據如何利用GIS手段管理和應用。文獻[7-9]闡述了大規模管線普查完成后,竣工測量和管線數據質量提升工作在管線管理中的地位,并為管線信息系統維護和應用提出了展望和要求。文獻[10]在討論道路曲線基本單元數字化數據處理模型的基礎上建立了道路曲線的聯合平差模型,探討了以線形為特征的道路數據的平差處理方法,提出了道路曲線數字化的精度評價方法,但未考慮特性線在三維空間的幾何特性。文獻[11]在研究經典整體最小二乘法的基礎之上,推導了非線性整體最小二乘平差計算模型并設計了迭代算法。文獻[12,13]基于空間向量,提出了空間圓形要素的擬合檢測方法,但需要觀測點位均勻分布于圓周,對地下管線而言,圓弧段只占整個圓周的局部,采用這種模型解算時存在較大不確定性。目前鮮有文獻針對管線探測數據的質量提升和評價做專門研究。本文在三維框架下,基于地下管線的固有線性幾何屬性,系統地探討了三維地下管線的數學模型,并提出了探測數據聯合平差模型和精度評價方法。

1 地下管線空間幾何特點

給水、熱力、燃氣、輸油和工業等地下管線一般為硬質管道,可以抽象為線段和圓弧兩類基本組成單元,不同單元之間通過三通、四通、分支點、轉折點、變材點、變坡點、變徑點、起訖點等節點連接。

在轉折點、變坡點,管線一般通過彎頭調整水平走向和豎向坡度,探測成果中三維管線夾角應與預制彎頭轉角參數值一致;管線段在交匯于三通、四通、變徑點、變材點時,一般具有相互垂直、共線、共面等幾何屬性;相鄰管線段(直線段間、直線與圓弧)存在共面關系;直、園相接時,二者在三維空間相切;新建管線和既有管線連接時,節點一般為檢查井內明顯點,其坐標較一般探測點量測精度更高,又因既有管線數據往往已做入庫管理,在精度滿足要求時,一般視其坐標值為已知量。

綜上所述,地下管線間存在以下幾何特性:①同一段管線上的點之間在三維框架下有共線、共弧關系,②相鄰的直線和圓弧應相切,相鄰直線段共面且夾角與設計參數一致,③在三通、四通、分支等聚合點上,相關管線具有共面、共線、垂直等幾何特性,④新增管線應附合到既有管線點上。

2 地下管線數學模型

由于管線由直線和圓弧組成,管線各點位坐標均可表示為空間直線和圓弧的相關參數的函數,因此可以將管線點坐標作為觀測值,采用間接平差方法建立平差模型,并將管線相切、夾角、匯聚、共面等作為限制條件。

按《工程測量通用規范》精度要求,地下管線測量精度為厘米級,對誤差方程和條件方程取泰勒展開式時,均可只取到一次項。本文對所有涉及角度均取弧度,故文中相關公式不涉及角度轉換。

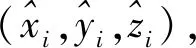
2.1 直線段誤差方程

如圖1所示,k1、k3分別為直線l投影在xoy面和xoz面直線l′的斜率(k1=tga),k2、k4則分別為相應的截距。則直線l的參數方程為:

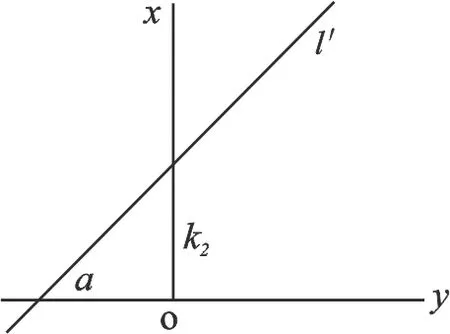
圖1

(1)

xi,k1,k,k3,k為未知參數,則相應誤差方程為:

(2)

2.2 圓弧段誤差方程

空間圓弧可視為xoy平面上的圓弧繞各個坐標軸旋轉并做平移后所得,由于圓弧上點和各旋轉角之間存在相關性,故只選用繞x軸的轉角φ和繞z軸的轉角k。則有圓弧參數方程:

(3)

(xc,yc,zc)T為圓心坐標,θi為弧段上諸點在原始狀態所對應半徑與x軸夾角。

取xc、yc、zc、k、φ、θi作為未知參數,當半徑不確定時,r也應作為未知參數。

因式(3)是一個非線性函數,采用泰勒公式展開,只保留一次項,可建立線性誤差方程(4):

(4)

對圓弧上每個點i,B為3×4的系數矩陣,各系數取值分別如下:

b32=0

2.3 條件方程

在以上誤差方程基礎上,考慮到管線段間的空間關系,還應存在以下條件方程:

(1)圓心到直線距離條件方程

空間直線l和圓弧c相切的充要條件是二者共面且圓心Pc到直線l的距離等于半徑。

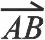
(5)

對式(5)做平方變換并線性化可得到以下線性條件方程:

(6)

其中:

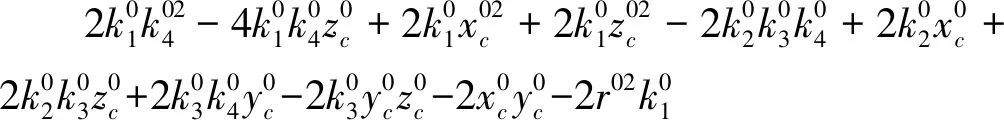
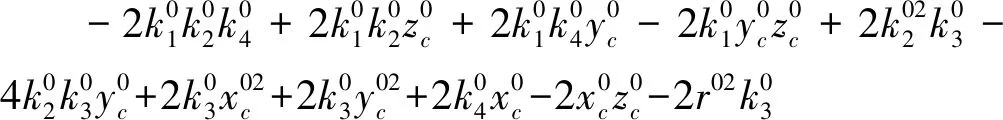
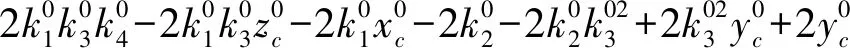
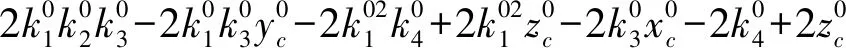
(2)直線和圓弧共面條件方程1

對直線l和圓弧c共面的情況,選直線l上A|x=0、B|x=1兩點、圓心Pc和圓平面內點P0|θ=0,r=1。依據式(3)可得,P0在空間的直角坐標為:

變換可得:

(7)

對式(7)線性化,得到下式:

(8)

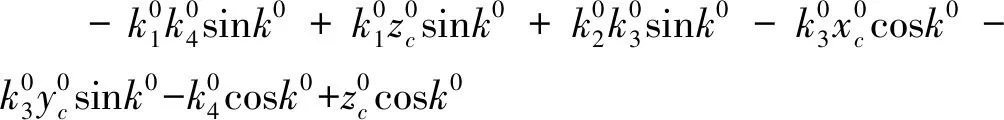
(3)直線和圓弧共面條件方程2

考慮到管線中的弧段一般只占圓周中一小段,而圓面和水平面夾角很小,只采用o-x一個方向約束線弧共面時,往往造成o-y方向誤差較大,故引入點PT|θ=90,r=1,依據式(3)計算可得P0在空間的直角坐標為:

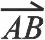
變換可得:

(9)

線性化后可得到條件方程(10):

(10)

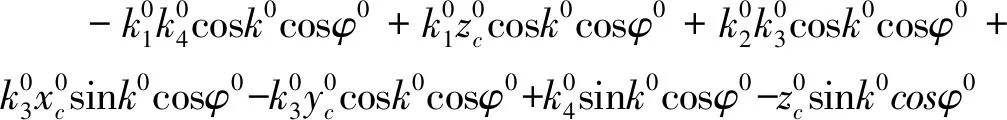
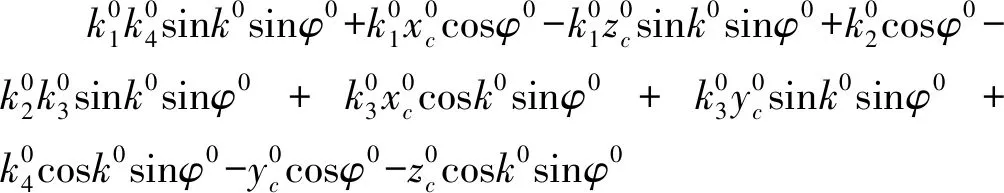
(4)直線相交(匯聚)條件方程

多條直線l1、l2…ln相交時,即存在x,使y1=y2=…=yn,z1=z2=…=zn,設l2的直線方程為:

y=k5x+k6z=k7x+k8

即可得條件方程(11):

(11)

當直線l2起止于Ps(xs,ys,zs)點時,還應存在條件方程(12):

(12)

(5)直線夾角條件方程

在線路通過預制彎頭轉折時,相鄰直線l1、l2在三維空間框架的夾角等于彎頭的轉角ω。

l1、l2的方向向量分別為v1=(1,k1,k3)和v2=(1,k5,k7),可得下式:

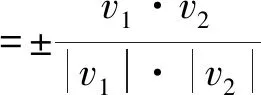
(13)

對地下管線,ω為轉角時,取cosω為正值,對式(13)線性化,得條件方程(14):

(14)

式中:u=cosω

對于管線垂直,可視為上式的特殊情況,即:

(15)

理論上也可將交點坐標、切點坐標或某個分量作為參數,構建誤差方程和條件方程,直接求解這些特征點的參數值,但由于直線段轉角往往為15°以下小角度,當探測管線點誤差較大時,交點、切點初始值偏差相應增大,會影響平差效果,本文未予采用。

3 觀測值權的確定

如表1所示,對明顯管線點,其X,Y坐標所對應權均為1,其高程所對應權為25/32。對覆土前施測的管線點,其X,Y坐標所對應權均為1,其高程所對應權為25/18。對于隱蔽點,其X,Y坐標所對應權為25/(52+(0.05h)2),其高程所對應權為25/(2(32+(0.075h)2))。

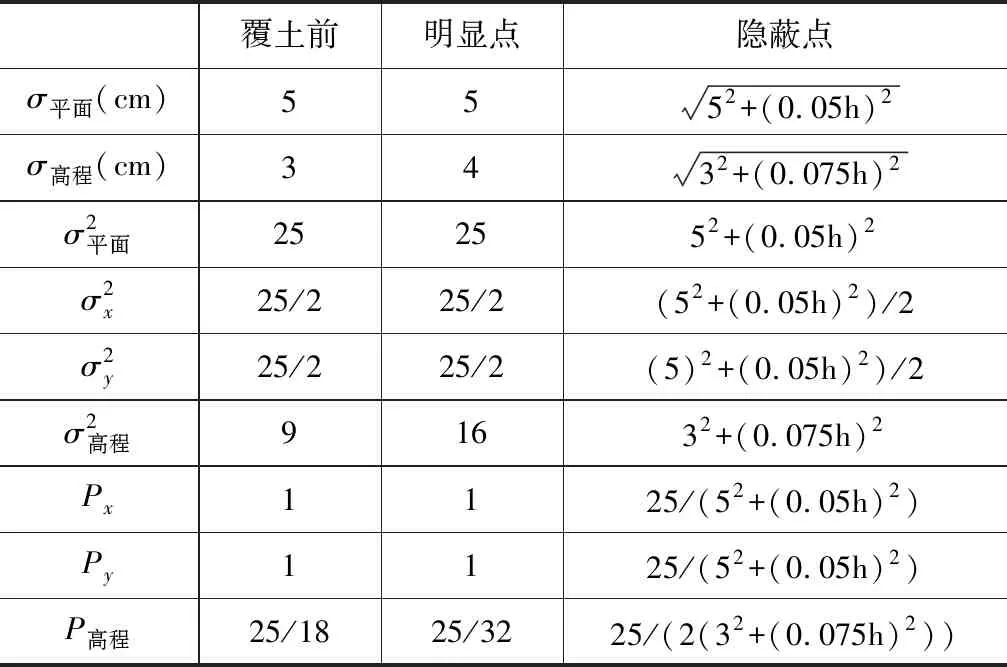
表1 觀測值先驗中誤差、權參考值

4 地下管線數據的聯合平差

從以上誤差方程(2)、(4)可以看到,在管線數據直線段參數有xi、k1、k2、k3和k4,必要觀測數為6(2點),圓弧段參數有xc、yc、zc、k、φ和θi,若弧段半徑未知時應納入半徑r,必要觀測數為9(3點),對每個點可按式(2)或(4)構造3個誤差方程。對直線-直線連接或匯聚,可按公式(11)構造空間相交條件方程,若直線段相互垂直或轉角(或夾角)已知參數,還應按公式(15)或(14)構造角度條件方程。對直線-圓弧連接,可按公式(6)、(8)和(10)分別按半徑和共面條件構造條件方程,若管線起訖點為已知點時,應按式(12)構造起訖點位附合條件方程。對于圓弧-圓弧連接的情況,在地下管線設計中一般采用直線段過渡,本文不予進一步研究。

近似值按照點位間距由遠及近原則,在各直線段和弧段選若干組點,分組計算k1、k2、k3和k4,以及xc、yc、zc、r、k、φ和θi等參數,采用中位數作為初始值。其中,φ為圓弧面和xoy面的夾角,k為圓弧面和xoy面的相交直線與x軸在xoy面的夾角。工作中,筆者采用該方法計算參數初始值1,構造誤差方程,利用間接平差求解參數2,然后將參數2作為新一輪初始值,重新構造誤差方程和條件方程,按附有限制條件的間接平差方法求解最終的改正數和參數值。

由于誤差方程和條件方程系數中有大量近似值,故采用迭代法解算。一般可采用單位權方差、觀測值殘差或相鄰兩次改正數之差等作為控制迭代循環的參考因子,如經過多次迭代,單位權方差不再收斂時,迭代運算即可終止。

在運算結束后,可逐一檢查各觀測值的殘差,當殘差大于二倍中誤差時,可視該點觀測值存在粗差,返回上一工序核查相關采集和計算資料,從而可有效實現粗差輔助定位。

完成平差后,利用直線和圓弧參數,計算交點、切點、起訖點等管線特征點坐標,并結合地面高程反算各點的埋深等屬性。

利用公式(16)計算管線的單位權方差,作為評定管線探測成果的質量和精度的指標:

(16)

式中:n-u+s為多余觀測數。

5 算 例

為方便計算,本文基于GIS系統環境,開發了管線平差模塊。作業時先將點位展繪到圖形系統中,再逐一選擇管線點并將點劃分到各個線(弧)段單元,完成分組后,指定各單元間的空間幾何關系,由模塊依次動態構建平差模型,最后完成統一平差。

以某段輸氣管線為例(圖2),該管道由一段圓弧c和兩段線段l1、l2組成,l1、l2轉角為45°,直線段探測點均為8點,弧段探測點為19點,將各點坐標作為觀測值,構造105個誤差方程,按各點探測深度計算觀測值的權,分別按c-l1共面、相切以及l1-l2相交與夾角為條件構造五個條件方程。利用中誤差作為迭代控制因子,經過3次迭代后,單位權方差不再收斂,結束運算。從表2數據可以看出,圓弧上存在一個粗差點,在對該點修正后重新計算,最終得到了較好的平差結果。

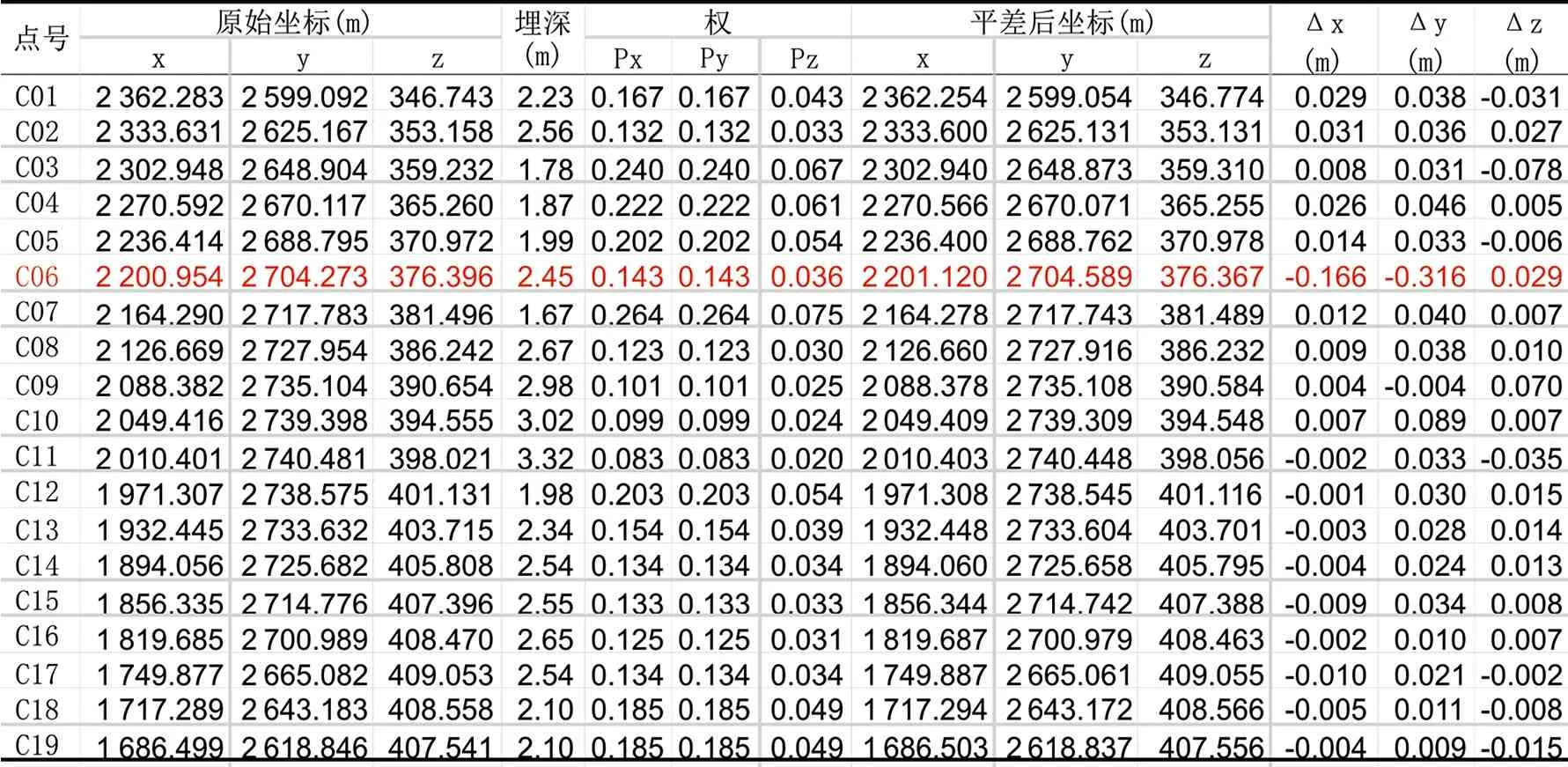
表2 計算結果

圖2 某段輸氣管線

6 結 論

基于三維空間直線和圓弧的數學基礎,本文提出了用直線和圓弧序列擬合管線探測值的平差模型并提出了探測數據權的確定方法,通過開發管線平差系統,實現了管線探測數據的粗差定位和平差處理,從而在提升管線探測數據精度的同時,使成果數據更符合管線的空間幾何特性,實現數據質量的有效提升。同時,該方法也可應用于異形建筑或其他由直線和圓弧構成的空間線性要素的擬合。