剛構(gòu)橋隨機地震動響應的簡明解析解及等效地震力計算
廖勇剛,張梨榮 ,葛新廣
(1. 廣西西江集團紅花二線船閘有限公司,廣西 柳州 545100; 2. 柳州工學院 土木建筑學院, 廣西 柳州 545004)
0 引言
橋梁工程是各類交通工程的重要構(gòu)成,其在地震過程中震害突出,影響巨大[1-3]。剛構(gòu)橋適用于大跨高墩結(jié)構(gòu),廣泛應用于市政、公路、鐵路及軌道交通工程中[4]。為了獲得更好的靜力學特性,剛構(gòu)橋構(gòu)造上采用強梁弱墩的布置形式,與其他類型橋梁相比,因采用梁-墩固結(jié),結(jié)構(gòu)剛度大,自振頻率較同跨度連續(xù)梁、簡支梁高,動力響應顯著。近年來,中國交通業(yè)的高速發(fā)展促進了剛構(gòu)橋的工程應用,全國各地建造了眾多剛構(gòu)橋項目,特別在一些震區(qū)。對剛構(gòu)橋地震動特性和動力響應分析是近年來工程界的研究熱點[5-8]。單德山等[9]研究了斷層距對大跨高墩連續(xù)剛構(gòu)橋的響應特點,研究表明:不同斷層距的大跨高墩連續(xù)剛構(gòu)橋梁的地震響應具有明顯差異,近斷層地震響應明顯強烈;閆曉宇等[10]基于振動臺試驗研究了近斷層效應對剛構(gòu)橋的動力響應,研究表明:近斷層對剛構(gòu)橋橋墩和主梁的跨中內(nèi)力與位移具有顯著影響。以上研究主要關(guān)注時程地震動激勵下對剛構(gòu)橋橋墩水平方向的動力響應分析,實際上地震動具有顯著的隨機性[11-12],且在順橋向水平地震作用下,橋墩產(chǎn)生側(cè)移使墩頂產(chǎn)生動彎矩進而引起梁跨結(jié)構(gòu)的豎向震動和水平震動。因此,研究順橋向水平隨機地震動作用下,剛構(gòu)橋順橋向和豎向耦合地震效應,對于確保剛構(gòu)橋抗震防災具有理論意義。
工程上,利用功率譜密度函數(shù)描述地震激勵的隨機性是一種主要方法,如白噪聲譜、Kanai-Tajimi譜、Clough-Pezien譜和歐進萍譜等[13-16]。基于功率譜模型的地震動響應分析,主要有時域法和頻域法[17-18]。時域法中結(jié)構(gòu)響應的協(xié)方差由地震激勵協(xié)方差與脈沖響應函數(shù)在時域的二重積分來表示,對于白噪聲激勵易于獲得響應的簡明解,但對于其他復雜地震動譜則存在響應計算復雜的問題。頻域法中,結(jié)構(gòu)響應的功率譜密度函數(shù)表示為地震動功率譜密度函數(shù)與響應量頻響函數(shù)模值平方的代數(shù)積,表達式簡潔因而得到廣泛應用,虛擬激勵法是其典型代表[18]。然而結(jié)構(gòu)安全評估和設(shè)計需要響應量的方差和譜矩,是基于響應量功率譜密度函數(shù)在頻域上的積分。現(xiàn)行《公路橋梁抗震設(shè)計規(guī)范》(JTJ/T 2231-01-2020)[19]采用功率譜法計算橋梁隨機地震動響應,應用時采用有效頻率區(qū)間的數(shù)值積分法進行近似計算。近年來,張俊等[12]和葛新廣等[21-22]針對傳統(tǒng)方法無法獲得封閉解的不足,提出了結(jié)構(gòu)響應方差和譜矩計算的封閉解法,所提方法無需數(shù)值積分運算。
針對多跨剛構(gòu)橋在順橋向水平地震作用下,墩梁固結(jié)處的墩頂部產(chǎn)生動彎矩進而使相連的橋跨結(jié)構(gòu)產(chǎn)生動彎矩,從而引起橋梁水平與豎向耦合振動的特征,提出了一種研究剛構(gòu)橋在順橋向隨機地震動作用下,水平和豎向耦合振動位移譜矩和等效地震力的新解析解法。首先,建立剛構(gòu)橋雙向地震動方程,基于MIDAS有限元軟件對剛構(gòu)橋進行離散化建模并獲得其豎向及順橋向振動的振型、自振圓頻率和節(jié)點集中質(zhì)量的動力參數(shù);其次,基于實模態(tài)解耦法,將整橋結(jié)構(gòu)節(jié)點位移表示為實模態(tài)振型的線性組合;再次,基于功率譜密度函數(shù)的二次化法[21-22],獲得了廣義變量及節(jié)點位移響應譜矩和方差的解析解法;最后,基于動力學等效原則獲得了剛構(gòu)橋節(jié)點等效地震力計算式。
1 剛構(gòu)橋地震動位移響應的頻域解
連續(xù)剛構(gòu)橋的結(jié)構(gòu)形式為邊墩與橋跨結(jié)構(gòu)采用支座連接而中墩與橋跨結(jié)構(gòu)采用剛性連接,動力學上常采用集中質(zhì)量法進行結(jié)構(gòu)離散化如圖1所示。順橋向地震動作用下橋墩的墩頂會產(chǎn)生動彎矩從而引起橋跨結(jié)構(gòu)產(chǎn)生動彎矩,進而引起橋跨結(jié)構(gòu)產(chǎn)生順橋向及豎向振動。為此,考慮全橋結(jié)構(gòu)順橋向水平及豎向振動自由度建立其動力方程為:

圖1 剛構(gòu)橋動力學簡圖Fig. 1 Dynamic calculating diagram of rigid frame bridge
(1)
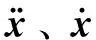
引入廣義坐標向量q,則剛構(gòu)橋節(jié)點位移向量表示為[23]:
x=φq
(2)
式中:q={q1,…,qN}T, φ為剛構(gòu)橋結(jié)構(gòu)前N階振型,為n×N階矩陣。
把式(2)帶入式(1)并利用實模態(tài)振型分析法,則基于廣義坐標地震動方程為:
(3)

由虛擬激勵法[18],式(3)所表示的廣義坐標的頻域解為:
(4)
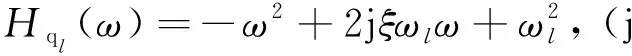
由式(2)及式(4),剛構(gòu)橋i節(jié)點處位移xi的頻域解為:
(5)
式中:φi,l為結(jié)構(gòu)實模態(tài)振型φ的第i行和第l列元素。
2 剛構(gòu)橋響應功率譜的二次分解式
由式(4)及虛擬激勵法[18],廣義坐標響應功率譜表示為:
(6)

由式(4)可知:對式(6)中的|Hql(ω)|2式進行二次式分解,即:
(7)

把式(7)帶入式(6),則廣義坐標的功率譜表示為:
(8)

由式(5)及虛擬激勵法[18],則位移響應的功率譜表示為:
(9)

對式(9)進行求和展開:
(10)
(11)
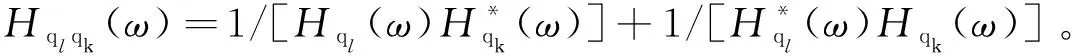
針對Hqlqk(ω)進行二次式化,具體見附錄A,其二次式為:
(12)
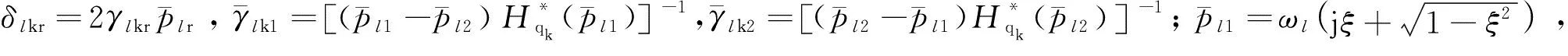
由式(11)和式(12),結(jié)構(gòu)位移響應功率譜表示為:
(13)


(14)
式中:ξf,ξg,ωf,ωg分別為場地土的振動特征值,S0為地震動強度系數(shù)。
由留數(shù)定理,對式(14)進行二次式分解為[23]:
(15)

3 結(jié)構(gòu)響應譜矩和方差的簡明封閉解
由隨機振動理論[17-18],剛構(gòu)橋位移響應和廣義變量的譜矩和方差表示為:

(16)

(17)
(18)
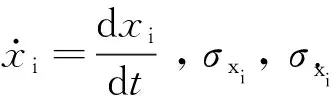
把式(8)帶入式(16)及式(13)帶入式(17)并進行積分,譜矩表示為:
(19)
(20)
式中:
(21)
(22)
對式(21)和式(22)進行積分,可獲得其解析解為:[23],
(23)
(24)
(25)
(26)
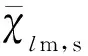
4 等效地震力的計算
工程設(shè)計常需要獲得結(jié)構(gòu)地震動作用下的內(nèi)力,以便與靜荷載工況結(jié)構(gòu)內(nèi)力進行荷載組合。在獲得隨機結(jié)構(gòu)動位移方差的基礎(chǔ)上,利用慣性力和動力學原理可獲得等效的節(jié)點地震力,是一種擬靜荷載,便于獲得地震作用下結(jié)構(gòu)的內(nèi)力值。
由結(jié)構(gòu)動力學可知[24]:線彈性結(jié)構(gòu)實模態(tài)解耦時,滿足下式:
(27)
基于式(27)、式(28)、式(29)和式(30),可獲得結(jié)構(gòu)體系無阻尼自振圓頻率ω和實模態(tài)振型φ。
由隨機振動理論[17-18],廣義變量二階導數(shù)標準差與廣義變量標準差存在關(guān)系為:
(28)

由式(2)和式(28)可知: 第i階振型的節(jié)點位移標準差向量可表示為:
(29)
式中:σxi和φi分別為第i階振型節(jié)點位移方差向量和第i階振型。
慣性力可表示為質(zhì)量與加速度的乘積,故節(jié)點慣性力向量可表示為:
(30)
在結(jié)構(gòu)體系確定時,由結(jié)構(gòu)力學的位移法可知,節(jié)點力可使結(jié)構(gòu)體系產(chǎn)生確定性節(jié)點位移;反之,當確定性節(jié)點位移已知,可反推出確定的節(jié)點力,
σFi=Kσxi
(31)
由式(27)、式(30)及式(31),結(jié)構(gòu)體系節(jié)點力標準差可表示為:
(32)
工程設(shè)計時,結(jié)構(gòu)設(shè)計響應值取峰值因子與響應量標準差的乘積,故第i振型的剛構(gòu)橋等效地震力可取:
(33)
式中,FE,i,cf為節(jié)點等效節(jié)點地震力向量,cf為峰值因子,《公路橋梁抗震設(shè)計》規(guī)范(JTJ/T 2231-01-2020)[19]取2.5。
利用式(33)可結(jié)構(gòu)實模態(tài)振型對應的節(jié)點等效地震力,并利用有限元軟件獲得結(jié)構(gòu)等效內(nèi)力,可SRSS法獲得多振型下的地震等效內(nèi)力設(shè)計值。
5 算例
某3跨預應力混凝土連續(xù)剛構(gòu)橋(跨度布置為60 m+110 m+60 m),采用變高度單箱單室截面,最大梁高7.0 m,最小梁高3.0 m,如圖2所示。1#墩和4#墩采用矩形實心墩(2 m×9 m),高分別為16.5 m和17.5 m;2#墩和3#墩采用凈距為1.3 m的雙薄壁墩(1.3 m×9 m),高分別為20.5 m和21.0 m。按8度設(shè)防,場地土為中硬土,雙過濾白噪聲激勵參數(shù):ωg=15.71 rad/s,ωf=0.4ωg,ξg=ξf=0.72,S0=111.34×10-4m2s-3。

圖2 剛構(gòu)橋動力學簡圖Fig. 1 Dynamic calculating diagram of rigid frame bridge
利用Midas軟件對剛構(gòu)橋進行有限元離散化可獲得剛構(gòu)橋的實模態(tài)振型和圓頻率。邊墩1#墩和4#墩與橋跨結(jié)構(gòu)采用球形橡膠支座進行連接,模擬時邊墩與主梁采用彈性連接,側(cè)向剛度取值為450 kN/m。剛構(gòu)橋結(jié)構(gòu)阻尼采用瑞雷阻尼,阻尼比取5%。
5.1 所提方法驗證
虛擬激勵法廣泛應用于各類工程的隨機動力響應分析[18],是目前分析隨機激勵下結(jié)構(gòu)動力響應最常用的方法。該方法在計算結(jié)構(gòu)響應0~2階譜矩和方差時,需要數(shù)值積分。為了驗證本文方法的正確性,利用虛擬激勵法及數(shù)值積分進行驗證。
圖3-8為采用虛擬激勵法和本文方法計算橋跨結(jié)構(gòu)豎向地震動和橋墩結(jié)構(gòu)水平向地震動的0~2階譜的對比圖。虛擬激勵法的ωu經(jīng)過試算取1000 rad/s,而Δω經(jīng)過試算分別取2.5 rad/s,1.0 rad/s,和0.1 rad/s。

圖3 橋跨結(jié)構(gòu)豎向位移0階譜Fig. 3 Zero-order spectral moments of bridge displacement in vertical direction

圖4 橋跨結(jié)構(gòu)豎向位移1階譜Fig. 4 First-order spectral moments of bridge displacement in vertical direction
從圖3-8可知:隨著虛擬激勵法中積分步長的變小,其計算結(jié)果越來越接近本文方法,從而說明了本文方法的正確性。虛擬激勵法中Δω=0.1 rad/s與本文方法的結(jié)算結(jié)果十分吻合,在相同的計算機環(huán)境下,耗時為36.38 s;而本文方法耗時為1.06 s,說明本文方法無需試算且具有較高的效率。
從圖3至圖5可知:橋跨結(jié)構(gòu)豎向地震動位移0~2譜矩,中跨的跨中最大;1#墩和4#墩處位移譜矩比邊跨跨中位移譜矩大很多。

圖5 橋跨結(jié)構(gòu)豎向位移2階譜>Fig. 5 Second-order spectral moments of bridge displacement in vertical direction
從圖6至圖8可知:2#和3#薄壁墩的兩分支墩順橋向位移譜基本相同,說明在橋墩構(gòu)件高度相同時,可認為結(jié)構(gòu)的地震動響應相同;對比0~2階譜中邊墩與中墩的位移譜矩關(guān)系,發(fā)現(xiàn)邊墩0~1階譜矩相對中墩較小,而2階譜矩的邊墩接近中墩,由于位移的2階譜矩代表節(jié)點地震動速度響應量,說明邊墩地震動位移較小,但其振動的速度可能會很大。

圖6 橋墩結(jié)構(gòu)順橋向位移0階譜Fig. 6 Zero-order spectral moments of longitudinal bridge displacement of piers

圖7 橋墩結(jié)構(gòu)順橋向位移1階譜Fig. 7 First-order spectral moments of longitudinal bridge displacement of piers

圖8 橋墩結(jié)構(gòu)順橋向位移2階譜Fig. 8 Second-order spectral moments of longitudinal bridge displacement of piers
5.2 等效地震力計算
利用式(33)計算剛構(gòu)橋橋跨基于前50階實模態(tài)振型的水平及豎向等效地震力,如圖9-10所示。
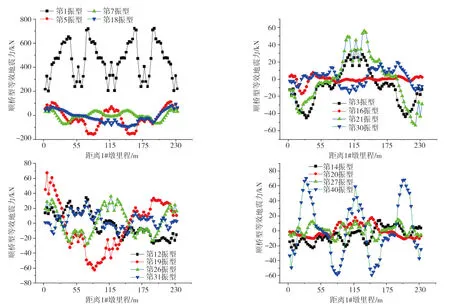
圖9 基于實模態(tài)橋跨結(jié)構(gòu)順橋向等效地震力Fig. 9 Horizontal equivalent seismic forces of bridge span structure based on real model
圖9及圖10分別列出了對梁跨結(jié)構(gòu)順橋向震動起主導作用的16個實模態(tài)振型對應的等效地震力,順橋向震動與水平向震動的主動振型各不相同,其中順橋向最高階主導振型為第40階,豎向最高階振型為第28階,說明剛構(gòu)橋橋跨結(jié)構(gòu)地震動響應分析均需要考慮高階振型。對比分析圖10,橋梁結(jié)構(gòu)豎向地震力數(shù)值較大,不能忽略。

圖10 基于實模態(tài)的橋跨結(jié)構(gòu)豎向等效地震力Fig. 10 Vertical equivalent seismic forces of bridge span structure based on real model
綜上所述,針對剛構(gòu)橋地震響應的分析,需考慮多振型的影響,且橋跨結(jié)構(gòu)的豎向振動不能忽略。
6 結(jié)論
論文研究了大跨度剛構(gòu)橋在順橋向地震動作用下,雙向地震動響應譜矩和方差的解析解及等效地震力的計算方法,取得了如下結(jié)論:
1)在獲得各節(jié)點等效地震力方差后,利用結(jié)構(gòu)力學的方法獲得全橋結(jié)構(gòu)的彎矩、剪力及軸力等內(nèi)力,然后利用SRSS方法可獲得剛構(gòu)橋構(gòu)件等效地震力作用下的內(nèi)力值,并可與作用在橋梁上的其他荷載作用下的內(nèi)力進行組合,從而可開展基于隨機振動理論的橋梁結(jié)構(gòu)抗震分析及動力可靠度分析。
2)針對剛構(gòu)橋在順橋向地震動作用下會產(chǎn)生順橋向水平和豎向地震動效應,兩種振動必須都要考慮;若采用實模態(tài)分解法進行地震動響應分析時,必須考慮多振型才能獲得正確解。
附 錄AHqlqk(ω)的二次式分解
針對Hqlqk(ω)進行整理:
(34)


由留數(shù)定理,式(34)可改寫為:
(35)

(36)
由于pl1是Hql(pl1)的根,所以式(36)改寫為:
(37)
對式(37)進一步簡化為:
(38)
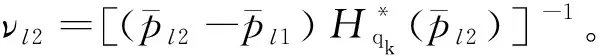
(39)
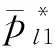
(40)
對式(40)進一步簡化為:
(41)
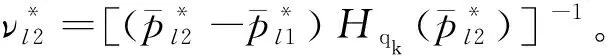
(42)
由式(42)及式(35)改寫為:
(43)
對式(43)整理后,則式(35)的二次式表示為:
(44)


