Quantum Stirling heat engine with squeezed thermal reservoir

Nikolaos Papadatos

Department of Physics,University of Patras,26500 Greece

Keywords: quantum heat engine,open systems,thermodynamics,performance characteristics

1.Introduction

1.1.Motivation

Over the past few years, the emerging field of quantum thermodynamics has attracted increasing attention in the scientific community, trying to find the quantum origin of the laws of thermodynamics.[1]Fundamental thermodynamic variables such as temperatureT,internal energyU,etc.,have been investigated extensively in terms of classical, statistical, quantum and relativistic quantum thermodynamics.[2-25]Furthermore, comprehension of the laws of classical thermodynamics is attainable, in the context of quantum heat engines (QHEs), by comparing thermodynamic quantities such as work and efficiency in terms of quantum variables.The QHE was first studied by Scovil and Schulz-DuBois in 1959 using a 3-level maser.[26]Thenceforward, the study of the performance of QHEs[27]has paved the way to new fields of research.In particular, the work and efficiency of QHEs,[28,29]have been analyzed with respect to the role of coherence,[30-36]the impact of entanglement,[37-40]the effect of a many-particle working medium,[41-46]the effect of the degeneracy factor in the energy levels,[47,48]fast Otto-cycles,[49]endoreversible Otto engines with a harmonic oscillator as the working medium,[50]endoreversible engines,[50-52]and an engine based on many body localization as a working fluid.[53]

One of the goals of studying quantum machines is to find ways to improve their overall performance.[54,55]Studies have emphasized that reinforcement-learning[56]and nonequilibrium quantum reservoirs,[57]coherent[58-60]and correlated,[61]can improve the performance of a quantum heat engine.Additionally, the concept of a squeezed thermal reservoir in quantum thermodynamics has started to attract increasing interest.The quantum Otto heat engine whose working medium is in contact with squeezed reservoirs has been studied extensively and presents some very interesting features.In particular, the efficiency at maximum power increases with the degree of squeezing,surpassing the standard Carnot limit.[62-69]In the real world, the efficiency at maximum power is a more important quantity than the maximum efficiency,at which power is zero.[70]The efficiency at maximum power was first studied by Curzon and Ahlborn(CA)[71]and they found thatwhereTcandThare the temperatures of the cold and hot reservoirs respectively.

The question arises as to what impact the squeezed thermal bath will have on another thermodynamic cycle, such as the Stirling thermodynamic cycle that has received less attention.The Stirling thermodynamic cycle has two isothermal and two isochoric processes[72]and produces more work than the Otto cycle does under the same parameters or equal efficiency conditions and operates a wider range of coupling strengths.[73]

The aim of this paper is to study the performance of a QHE in which the working medium interacts with a pure cold reservoir and a squeezed thermal reservoir.[74-76]In particular,we analyze the quantum equivalent of the classical Stirling cycle[77-92]in which the hot reservoir is replaced by a thermal squeezed reservoir.We observe that the squeezing parameterrhimproves the performance of a QSHE,especially when the ratio of the temperatures of the hot and cold reservoirs is small,which means that the engine has less energetic cost.In order to compare the efficiency of the QSHE with the Carnot limit we introduce an effective temperature so that the steady state of the system under review can be seen as a thermal equilibrium state but at temperatureTeff.[93-96]On the other hand,the generation of squeezing has a thermodynamic cost which depends on the specific configuration employed.[97,98]Generally speaking,when the cost of generating a squeezed state is included in the computation of the efficiency of the engine,the squeezed reservoirs are costly.[99]However, we focus on studying the performance of a QSHE without including the energy losses from the generation of squeezing.

1.2.Analysis and results

Our QHE consists of a working medium that is weakly coupled to a pure cold reservoir and a squeezed thermal reservoir alternately according to the Stirling thermodynamic cycle.We analyze two cases as far as the working medium is concerned,a two-level system and a harmonic oscillator.Our results are the following:

(i) We derive closed-form expressions for the produced work and efficiency which strongly depend on the squeezing parameterrh.

(ii) In the case of both working mediums, the produced work and the efficiency of the QSHE increase with the degree of squeezing,see Figs.1-9.

(iii)The performance of the QSHE,i.e.,the efficiency and the total produced work,depends on the nature of the working medium,see Figs.1-9.

(iv)The effective temperature due to squeezing is always higher than the temperature of the thermal reservoir.

(v)We derived the analytic expressions for the efficiency at maximum work and the maximum produced work in the high and low temperature regimes.

(vi) In the low temperature regime, the efficiency of the QSHE with a two-level system as a working medium coincides with the efficiency of the quantum Otto heat engine.

(vii)At extreme temperatures the squeezing parameterrhdoes not affect the performance of the QSHE.

The structure of this paper is the following.In Section 2 we examine the first case of a QSHE with a two-level system as a working medium.In Section 3,we examine the second case of a QSHE with a harmonic oscillator as the working medium.The conclusions are presented in Section 4.

2.Quantum Stirling heat engine - Two-level atom

In this section, we use a two-level system (TLS) of frequencyωas the working medium, which interacts with a squeezed thermal reservoir in the Born-Markov,rotating-wave approximation.The system Hamiltonian is given byH=ωσz.The evolution of the reduced density matrix operator of the system in the interaction picture has the following form:[100]

HereΓis the spontaneous emission rate andσ+,σ-are the raising and lowering operators respectively,where

is the mean number of quanta,Ththe temperature,rhthe squeeze parameter andφthe phase.We notice that the asymptotic state does not depend on the squeezed phaseφ.

and,equivalently,we have

The interaction of a two-level quantum system with a squeezed environment causes a geometric phase (GP) or Berry phase(BP).The dependence of the GP on temperature and squeezing shows complexity.[101]However,equation(1)is valid only when the interaction between the system and the environment is very weak and the environmental correlation time is very small,or,in other words,if the time-scale of the external driving is much larger than the inner relaxation scale of the quantum dynamics of the system.[102-105]

The expectation value of energy is given by

thus,

As far as the interaction of the working medium with the pure cold reservoir is concerned, analogous expressions can be obtained from the above relations by setting these squeezing parameters to zero and the temperature toTc.

The quantum Stirling heat engine is the quantum counterpart of the classical Stirling thermodynamic cycle.It consists of two isothermal processes and two isochoric processes.In the first case, as the working medium, we have a two-level system that interacts with a hot squeezed reservoir and a cold bath alternately so as to perform a quantum Stirling thermodynamic cycle.The general quantum Stirling cycle has the following four steps repeated cyclically:

(i) Isothermal expansionA(ω2,Th)→B(ω1,Th).Initially, the TLS is in contact with the hot squeezed reservoir at a constant temperatureThthat can be described by a unitary squeezed operator with squeezed parametersrhandφ.During this process the mean number of quanta and the energy gaps must change simultaneously in order for the system to remain in an equilibrium state.This process will occur slowly enough to allow the system to remain in equilibrium with the thermal bath continuously.The frequency reduces fromω2to a smaller valueω1and the heat transferred isQAB=ThΔSAB.

(ii)Cold isochoricB(ω1,Th)→C(ω1,Tc).In the second stroke, the TLS is disconnected from the hot squeezed bath and is connected with the cold bath at temperatureTcwith fixed frequency.

(iii)Isothermal compressionC(ω1,Tc)→D(ω2,Tc).In the third stroke,the TLS is still coupled with the cold bath and the frequency increases fromω1to a bigger valueω2.The heat transferred isQCD=TcΔSCD.

(iv) Hot isochoricD(ω2,Tc)→A(ω2,Th).Finally, at constant frequency the TLS is disconnected from the cold bath and is connected with the hot squeezed bath at temperatureThwith fixed frequency.

The entropy for a TLS at thermal equilibrium is

thus

We compute the entropy change in processAB

where

Consequently,the heat from this process is

and from Eq.(11)we obtain

The heat absorbed in the isothermal processABusing a thermal squeezed reservoir (15) has the usual form but with coefficients that contain the squeezing parameterrh.In the limitrh→0,Eq.(15)takes the form

The work output per cycle according to the first law of thermodynamics is Refs.[3,106]

The expectation value of energy from Eq.(8)is

The expectation value of work is

where

Following the same procedure as before we compute the heat and work in the third stroke

In the quantum isochoric process, no work is done, and thus the absorbed or released heat is

The total work is computed from Eqs.(19) and (22),W=WAB+WCD,thus

In Figs.1 and 2 we plot the produced workW/(kBTc)of the QSHE as a function of the ratio of frequenciesω2/ω1and temperaturesTh/TCrespectively, with different values of the squeezing parameterrh.We notice that the squeezing parameterrhplays a pivotal role in the work production due to the fact that the work is maximum even if the ratio of hot and cold temperatures is small,meaning less energetic cost.

The system absorbs heat only during the first isothermal stroke and the final isochoric stroke, thus, the total heat absorbed during a complete cycle

When the average heat〈?Q〉H ≥0 it is absorbed from the hot squeezed reservoir,and when the average heat〈?Q〉C ≤0 it is absorbed from the cold thermal reservoir.The mean work〈?W〉ab ≥0 expresses the consumed work by the system and〈?W〉cd ≤0 means that the system produces work.

The efficiency of the QHE is the proportion of the total work per cycle with respect to the heat absorbed from the hot thermal reservoir:

In Fig.3,we plot the efficiencyηSof our cycle as a function of the squeezing parameterrhand compare it with the Carnot and Curzon-Ahlborn efficiencies.[71]We notice that the squeezing parameterrhincreases the efficiency,especially when the ratio of temperatures is small, and the efficiency tends to the Curzon-Ahlborn efficiencyηCA,which is the efficiency at maximum work.[107]On the other hand, when the ratio of temperaturesTh/TCincreases the squeezing parameter cannot improve the performance of the QSHE so as to surpass the Carnot efficiencyηC.

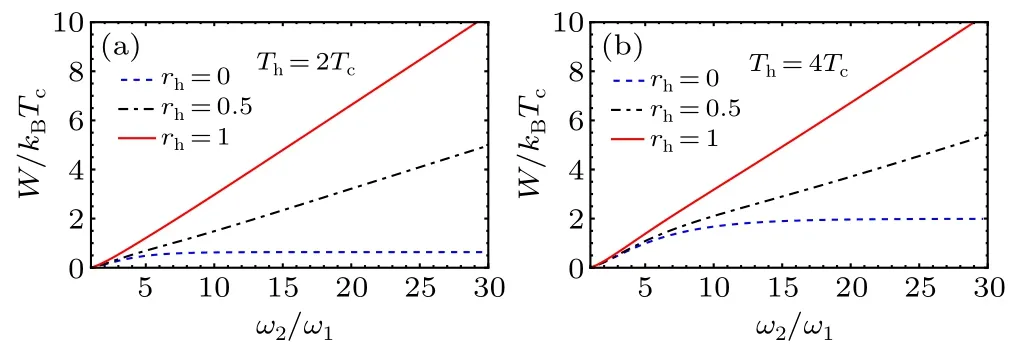
Fig.1.Total work output W/(kBTc)as a function of the frequency modulation ω2/ω1,for different values of the squeezed parameter rh.

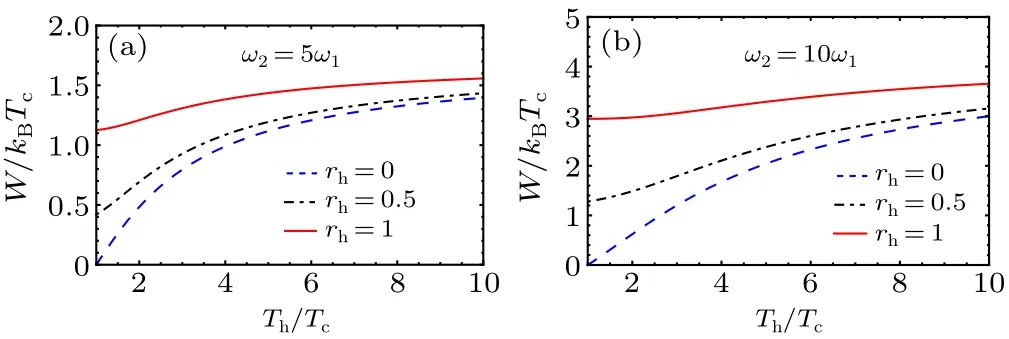
Fig.2.Total work output W/(kBTc) as a function of the temperature Th/Tc,for different values of the squeezed parameter rh.

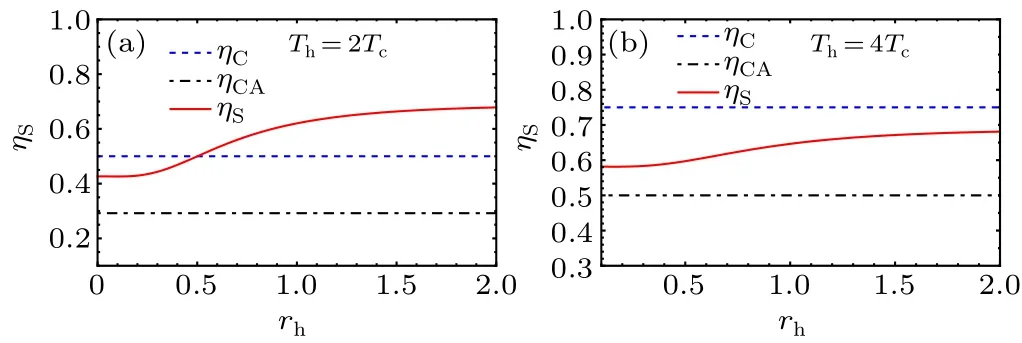
Fig.3.Efficiency of the heat engine as a function of the squeezing parameter rh in comparison to the Carnot ηC and Curzon-Ahlborn ηCA efficiencies.Others parameters are ω2=5ω1.

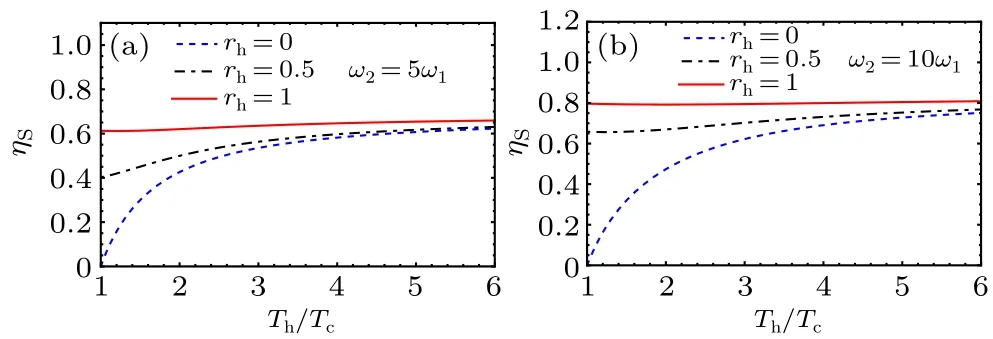
Fig.4.Efficiency of the heat engine as a function of the temperatures Tc/Th for different ratios of frequencies.

In Fig.5 we plot the efficiency of the QSHE as a function of the squeezing parameterrhand ratio of frequenciesω2/ω1.Moreover,we compare it with the Carnot efficiency and show that the efficiency increases with the increase ofω1=kBTc/ˉhas well as withrh,and for some values of these parameters the QSHE surpasses the Carnot limit.

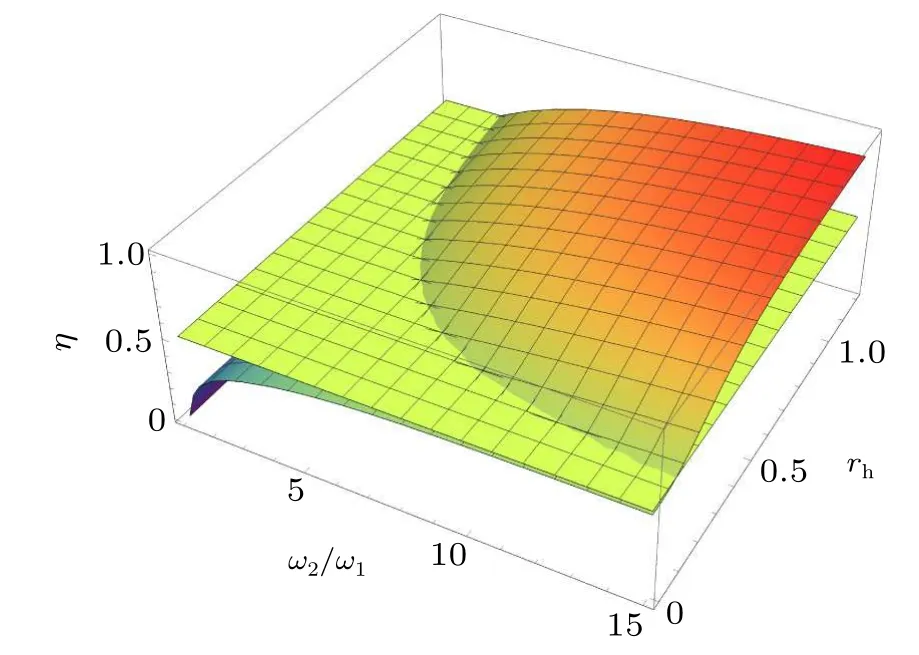
Fig.5.Efficiency of the heat engine as a function of ω2/ω1 and the squeezing parameter rh for Th=2TC in comparison with the Carnot efficiency.

We highlight that the efficiency of the QSHE with squeezed thermal reservoir surpasses the standard Carnot limit when the ratio of the hot and cold baths’temperatures is small.This interesting result is caused when the squeezing parameterrh→1, and its mechanisms can be explained as follows.At the end of the quantum isochoric process,the asymptotic state of the two-level system is given by Eq.(6).Whenrh→0 the asymptotic state of the two-level system is given by

wherenis given by Eq.(4).In contrast, whenrh＞0, the asymptotic state of the two-level system is given again by Eq.(28) but with an effective temperature that contains the squeezing parameterrhand the temperatureT,

andTeffis always higher thanTdue to the squeezed parameters

Let us now proceed to examine the high temperature limit,ω/Th→0.The total produced work in the first order approximation is

We use the second derivative test with respect to the ratio of frequenciesω2/ω1[108]in order to find the maximum value of the produced work.In this case the produced work does not have a local maximum value.

Next, we compute the efficiency in the high temperature regime in the second order approximation

Let us now proceed to examine the low temperature limitω/TC→∞.The total produced work is

where the first and second terms are the first and second order approximations respectively.The maximum work is when

The efficiency in the low temperature regime is

which coincides with the efficiency of a quantum Otto heat engine,[109,110]and is independent of the squeezing parameterrhas it depends on the ratio of the frequencies only.The efficiency at maximum work is taken from Eqs.(33)and(34).

The second order approximation of the efficiency,which depends on squeezing parameterrh,is

3.Quantum Stirling heat engine - Harmonic oscillator

In this section we examine the harmonic oscillator as the working medium of the QSHE.First, we discuss the thermal squeezed state of the harmonic oscillator.For a harmonic oscillator of massmand frequencyω,the squeezed thermal state results from the application of the squeezing operator to the thermal equilibrium state.The density matrix is as follows:

where ?ρGis the Gibbs state of the harmonic oscillator, and ?S(ξ)is the squeezed operator,

andξ=reiθis a complex number withr ≥0 called the squeezing parameter withθ ∈[0,2π].The internal energy of the harmonic oscillator in a squeezed thermal state is[111]

where

In an analogous way,as in the first part of this work, we construct the four strokes of the QSHE with the harmonic oscillator as the working medium,[112]and then we compute the expectation value of energy of each process,thus

Consequently,the heat in the isothermal processABis

where

The expectation value of work in this process is obtained from the first law of thermodynamics

In the quantum isochoric processes,no work is done,and thus the absorbed or released heat is

Following the same procedure as before we compute the heat and work in the third stroke

Consequently,the total produced work is

In Figs.6 and 7,we show that the total produced work increases monotonically from zero as a function of the frequency ratio with respect to the increase of the squeezing parameterrh.

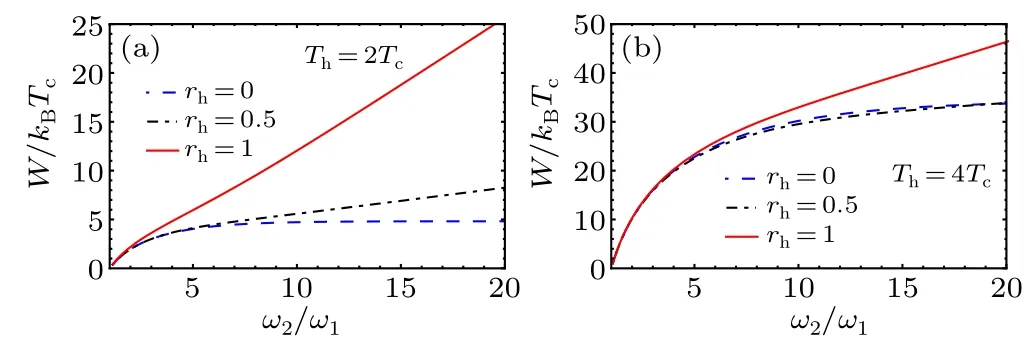
Fig.6.Total work output W/(kBTc)as a function of the frequency modulation, ω2/ω1, for different values of the squeezed parameter rh and temperature ratio.

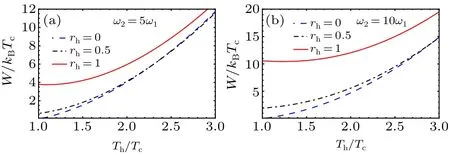
Fig.7.Total work output,W/(kBTc)as a function of temperatures ratio,Th/TC, for different values of the squeezed parameter rh and frequency ratio.

Furthermore,we compute the efficiency of the QSHE

Due to the fact that the analytical expression of the efficiency of the QSHE is complicated, we plot the numerical results in Figs.8 and 9.In Fig.8 we plot the efficiency as a function of squeezing parameterrhand compare it with the Curzon-AhlbornηCAefficiency and the efficiency of the classical Stirling heat engine, which is the same as the Carnot efficiencyηC.We show that increasingrhcan improve the efficiency of the QSHE so as to approach and surpass the Carnot limit.

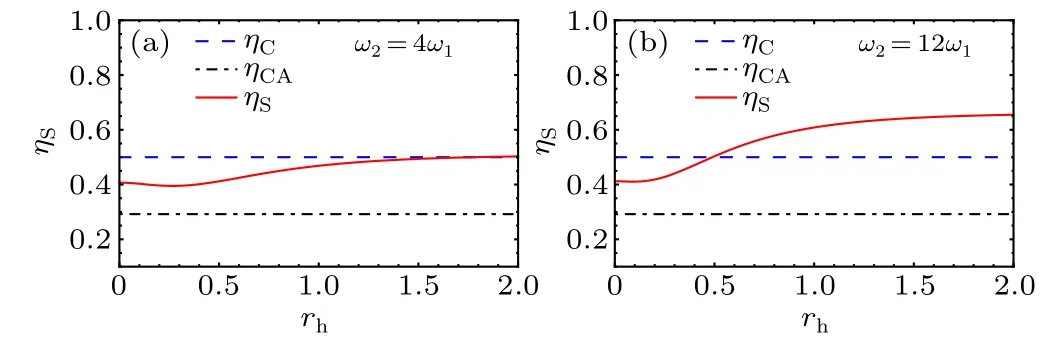
Fig.8.Efficiency η as a function of the squeezed parameter rh for different frequencies of the oscillator ω1=kBTc/ˉh in comparison to the Carnot ηC and Curzon-Ahlborn ηCA efficiencies.Other parameters are Th=2Tc.

In Fig.9 we plot the efficiency of the QSHE as a function of the squeezing parameterrhand ratio of frequenciesω2/ω1.Moreover,we compare it with the Carnot efficiency and show that the efficiency increases with the increase ofω1=kBTc/ˉhas well as withrhand that for some values of these parameters the QSHE surpasses the Carnot limit.

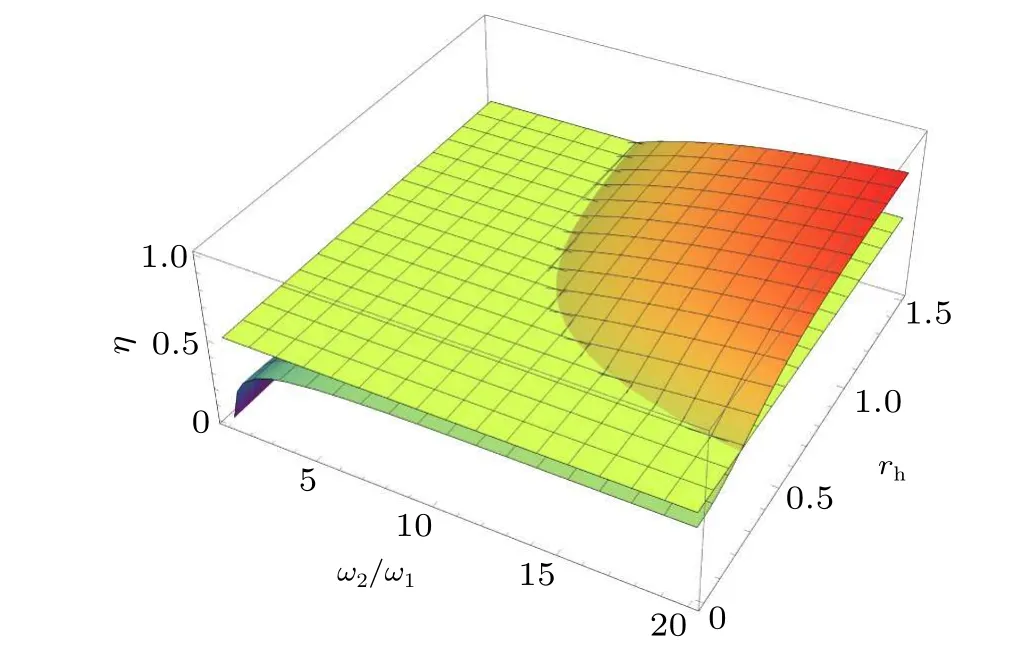
Fig.9.Efficiency of the QSHE with respect to ω2/ω1 and the squeezing parameter rh in comparison with the Carnot efficiency.The oscillator’s frequency is ω1=kBTc/ˉh.

Let us now proceed to examine the high temperature limitω/Th→0.The total produced work is

where the first term is the first order approximation and the rest of the terms are derived from the second-order approximation.Following the same procedure as in the first part of this work,we find that the maximum work is when

Consequently, the efficiency at maximum work in the high temperature regime is

Let us now proceed to examine the low temperature limitω/TC→∞.The total produced work is

where the first two terms are the first order approximation.The maximum work is when

Consequently,the efficiency at maximum work in the low temperature regime is

4.Conclusion

In this paper,we have investigated a quantum Stirling heat engine(QSHE)with a two-level system and a harmonic oscillator as the working medium that is in contact with a squeezed thermal reservoir and a cold reservoir.We obtained closedform expressions for the produced work and efficiency which depend strongly on the squeezing parameterrh.Then we proved that the effect of squeezing heats the working medium to a higher effective temperature leading to a better overall performance.In particular, the efficiency increases with the degree of squeezing surpassing the standard Carnot limit when the ratio of the temperatures of the hot and cold reservoirs is small, which means that the engine has less energetic cost.Additionally,we derived the analytic expressions for the efficiency at maximum work and the maximum produced work in the high and low temperature regimes.We found that the efficiency in the low temperature regime coincides with the efficiency of a quantum Otto heat engine and is independent of the squeezing parameterrh,depending only on the ratio of frequencies.We noticed that in the first order approximation the efficiency at maximum work and the maximum produced work are independent of the squeezing parameterrh.In contrast,the aforementioned result in the second order approximation depends on the squeezing parameterrh.This means that at extreme temperatures the squeezing parameterrhdoes not affect the performance of the QSHE.This phenomenon is expected because the system loses its quantum features and the state becomes classical,i.e.,a mixture of coherent states,losing its entanglement potential and other quantum features.[113,114]Finally,the performance of the QSHE depends on the nature of the working medium.Thus,in future work,we will extend the corresponding analysis for different working mediums, such as spin-1/2 systems[29,115,116]and coupled oscillators.[117]