基于頻域信息融合和稀疏貝葉斯學(xué)習(xí)的高分辨ISAR成像
景鑫磊,張 宇,蔣忠進(jìn)
(東南大學(xué)毫米波國家重點實驗室,江蘇南京 210096)
0 引言
逆合成孔徑雷達(dá)(Inverse Synthetic Aperture Radar,ISAR)成像作為一種重要的偵測手段,可以全天候、全時段對非合作機動性目標(biāo)進(jìn)行成像[1-2]。但是,因為非合作目標(biāo)的運動補償建模比較復(fù)雜,積累轉(zhuǎn)角和回波多普勒帶寬受限,傳統(tǒng)的ISAR 成像算法,如Range Doppler(RD)算法,其成像分辨率受到限制,因此研究超分辨ISAR 成像算法具有重要意義。
MUSIC 算法和ESPRIT 算法是兩種傳統(tǒng)的參數(shù)化ISAR 成像算法。但MUSIC 算法的分辨率不是很高,酉ESPRIT 算法是一種超分辨算法,但該算法只能在距離維或者方向維實現(xiàn)超分辨,無法在兩個維度同時實現(xiàn)超分辨成像[3]。
壓縮感知(Compressed Sensing,CS)理論適合于稀疏參數(shù)的高分辨重構(gòu)[4],并且ISAR 圖像中的強散射點滿足稀疏分布特性,所以CS 在超分辨ISAR成像中得到越來越多的研究和應(yīng)用。稀疏信號恢復(fù)的出發(fā)點是在L0范數(shù)最小化的基礎(chǔ)上進(jìn)行參數(shù)重構(gòu),但這是一個NP 難問題,壓縮感知理論在一定條件下,可以將L0范數(shù)最小化約束放寬為L1范數(shù)最小化約束,于是涌現(xiàn)出BP 算法[5]、梯度下降算法[6]以及迭代ISTA算法[7]等參數(shù)重構(gòu)算法,但是這些算法在感知矩陣列相關(guān)性強的時候性能會出現(xiàn)下降,影響ISAR 成像效果。文獻(xiàn)[8]采用光滑函數(shù)來近似L0范數(shù)并進(jìn)行稀疏參數(shù)重構(gòu),但該算法中的正則參數(shù)需要人為手動設(shè)置,影響了算法的實用性。
文獻(xiàn)[9]提出了基于稀疏貝葉斯學(xué)習(xí)(Sparse Bayesian Learning,SBL)框架的ISAR 成像算法,取得了不錯的效果。相比于傳統(tǒng)的SMV 模型[10],MMV-SBL 模型避免了Kron 內(nèi)積導(dǎo)致的感知矩陣尺寸過大問題,以及大尺寸逆矩陣計算問題[11]。文獻(xiàn)[12]提出一種BI-MSBL 算法,該算法利用冗余信息的融合去除徑向插值帶來的條紋,獲得更清晰的ISAR 圖像。文獻(xiàn)[13]則提出一種LS-SBL算法,利用目標(biāo)自身的結(jié)構(gòu)特征構(gòu)建結(jié)構(gòu)化先驗?zāi)P秃蛥?shù)化字典,對旋轉(zhuǎn)運動目標(biāo)進(jìn)行ISAR 成像,取得較為理想的成像效果。文獻(xiàn)[14]引入LSM(Laplace Scale Mixture)尺度混合先驗?zāi)P停⑼ㄟ^拉普拉斯估計(Laplace Approximation,LA)和變分貝葉斯(Variational Bayesian,VB)算法求解散射系數(shù)的后驗分布,以此得到更稀疏更精確的ISAR圖像。
為了在ISAR 成像中更好地壓制噪聲,消除條紋干擾,提高成像分辨率,本文提出一種基于雙向插值處理(Bidirectional Interpolation Process)和頻域信息融合(Information Fusion in Frequency Domain)的稀疏貝葉斯學(xué)習(xí)算法,簡稱BI-FF SBL 算法。該算法引入LSM 先驗來為回波信號構(gòu)建MMV SBL 模型,并采用LA-VB 算法進(jìn)行目標(biāo)散射系數(shù)的重構(gòu)。首先對回波信號分別進(jìn)行徑向和橫向插值預(yù)處理,將預(yù)處理得到的兩份數(shù)據(jù)通過LAVB SBL 算法進(jìn)行ISAR 成像;然后將得到的兩幅ISAR 圖像通過二維傅里葉變換進(jìn)入頻域,并將兩個二維頻譜進(jìn)行信息融合處理,以消除噪聲和條紋干擾的相關(guān)信息并保留目標(biāo)結(jié)構(gòu)信息;最后對融合處理后的頻譜進(jìn)行二維傅里葉逆變換,得到最終的ISAR圖像。
1 信號模型
假設(shè)已對雷達(dá)回波信號作平動補償,則ISAR成像模型可視為轉(zhuǎn)臺模型,ISAR 成像的原理圖如圖1所示,其中雷達(dá)向目標(biāo)發(fā)射線性頻率調(diào)制(LFM)脈沖。由于雷達(dá)到目標(biāo)中心的距離遠(yuǎn)遠(yuǎn)大于目標(biāo)的尺寸,因此雷達(dá)電磁波被視為以平面波的形式照射到目標(biāo)上,并假定目標(biāo)以恒定的角速度旋轉(zhuǎn)。
回波HRRP 數(shù)據(jù)是通過對接收信號進(jìn)行徑向脈沖壓縮得到的,其理想點散射中心模型可以表示為
式中:s(θ,f)表示進(jìn)行徑向傅里葉變換后的HRRP數(shù)據(jù),θ表示發(fā)收信號的目標(biāo)轉(zhuǎn)角,f表示脈沖發(fā)射頻率;w(y,x)表示目標(biāo)散射系數(shù);c表示電磁波速度;R0表示從雷達(dá)到目標(biāo)中心的遠(yuǎn)場距離。
對成像的角度和頻率,以及二維場景進(jìn)行離散化處理。在以目標(biāo)中心為原點的局部坐標(biāo)系中,散射區(qū)域被離散為P行和Q列,得到
式中:fc為載波頻率;fn為第n個離散頻率,n=1,2,…,N;θm為第m個脈沖對應(yīng)的目標(biāo)轉(zhuǎn)角,m=1,2,…,M;w(yp,xq)代表坐標(biāo)(yp,xq)處的散射系數(shù),其中p=1,2,…,P,q=1,2,…,Q。
將上式經(jīng)過一系列的推導(dǎo)和化簡,并添加環(huán)境噪聲U,可得到回波信號的矩陣表達(dá)式為
式中,S∈CM×N表示回波信號矩陣,W∈CP×Q表示散射系數(shù)矩陣,U∈CM×N表示復(fù)高斯白噪聲,Φc∈CM×P和Φr∈CQ×N分別表示方向維和距離維的部分傅里葉矩陣,可將其展開為
2 BI-FF SBL算法
本文提出一種基于雙向插值處理和頻域信息融合的稀疏貝葉斯學(xué)習(xí)算法,此處簡稱BI-FF SBL算法,并將其用于高分辨ISAR成像。
2.1 徑向插值預(yù)處理
2.2 橫向插值預(yù)處理
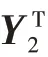
2.3 基于LA-VB算法的參數(shù)重構(gòu)
在傳統(tǒng)的MMV-SBL算法中,回波信號的MMV模型可以表示為
式中,Y∈CM×Q,Φ∈CM×P,W∈CP×Q與N∈CM×Q分別表示回波信號矩陣、感知矩陣、散射系數(shù)矩陣和噪聲矩陣。

令矩陣Y的列與列之間統(tǒng)計獨立,則Y的似然函數(shù)可寫為



由完全貝葉斯推導(dǎo)得出的近似后驗概率分布的期望可以用來作為未知參數(shù)的后驗估計,因此超參數(shù)λp,q和β的MAP估計可通過推導(dǎo)得出:

2.4 頻域融合
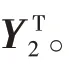
(c)融合Z1與Z2而得到最終的頻率圖像Z:

(d)對頻率圖像Z作二維傅里葉逆變換得到最終的ISAR圖像?。
3 實驗結(jié)果與對比分析
為了驗證BI-FF SBL 算法的有效性,本文基于電磁仿真數(shù)據(jù)和實測數(shù)據(jù)完成了ISAR 成像實驗。在實驗中測試了4種不同的算法,包括R-D(Range-Doppler)算法、L1-BP算法、LA-VB算法以及本文提出的BI-FF SBL 算法,并將不同算法的ISAR 成像結(jié)果進(jìn)行對比。
為了檢驗不同算法抑制噪聲的能力,在仿真數(shù)據(jù)和實測數(shù)據(jù)中加入復(fù)高斯噪聲,合成了信噪比分別為0,5和10 dB的實驗數(shù)據(jù)。
3.1 仿真數(shù)據(jù)實驗
在基于仿真數(shù)據(jù)的實驗中,ISAR 成像目標(biāo)是A-10攻擊機,其CAD模型如圖2(a)和(b)所示。回波信號由高頻電磁仿真代碼生成,入射頻率為9.5~10.5 GHz,中心頻率為10.0 GHz,帶寬為1 GHz,共掃描128 個頻率點。入射俯仰角為94°,入射中心方位角為135°,方位角寬度為5.729 6°,共掃描128 個方位角點。得到的回波信號矩陣尺寸為128×128。徑向和橫向分辨率均為0.15 m,成像面積為19.2 m×19.2 m。

圖2 A-10攻擊機CAD模型圖
實驗采用前文所述的4種算法,每種算法均在0,5 和10 dB 三個信噪比下進(jìn)行ISAR 成像,成像結(jié)果如圖3所示。
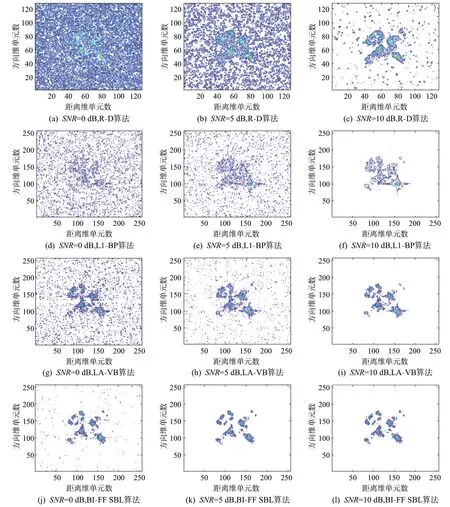
圖3 不同信噪比下各類算法的仿真ISAR成像效果圖
從圖3 可以看出,在信噪比為0 dB 時,由于噪聲的影響,傳統(tǒng)R-D 算法和L1-BP算法已經(jīng)近乎失效;LA-VB 算法雖然可以粗略重構(gòu)出飛機的幾何結(jié)構(gòu),但是ISAR 圖像受噪點影響嚴(yán)重,只能模糊地重構(gòu)出機頭和機身處部分強散射點;本文的BIFF SBL 算法可以給出較為清晰的ISAR 圖像,雖然圖像中也分布有一些噪點,但仍然很好地保留了飛機的幾何結(jié)構(gòu)特征。
在信噪比為5 dB 時,各類算法的成像效果均有所提升,但R-D算法所成ISAR圖像仍較為模糊,由L1-BP算法和LA-VB算法重構(gòu)的ISAR圖像中存在較多噪點,而BI-FF SBL 算法則可以給出清晰的ISAR圖像。
在信噪比為10 dB 時,各類算法所成ISAR 圖像均能清晰地體現(xiàn)飛機的幾何結(jié)構(gòu)特征。但是R-D算法所成圖像分辨率很低,圖中仍然存在較多噪點;L1-BP算法所成圖像分辨率低于LA-VB 算法和BI-FF SBL算法。
3.2 實測數(shù)據(jù)實驗
實測數(shù)據(jù)為ISAR 成像系統(tǒng)錄取的Yak-42 飛機回波信號,中心頻率為5.52 GHz,發(fā)射帶寬為400 MHz,脈沖重復(fù)頻率為400 Hz。實驗采用的回波信號矩陣的尺寸為128×128,通過添加復(fù)高斯白噪聲以獲取信噪比分別為0,5 和10 dB 的實驗數(shù)據(jù)。
實驗采用前文所述的4種算法,每種算法均在0,5 和10 dB 三個信噪比下進(jìn)行ISAR 成像,成像結(jié)果如圖4所示。
如圖4所示,信噪比為0 dB 時,4 種算法的ISAR 成像結(jié)果中都存在不同程度的噪點,其中R-D 算法的成像效果最差;L1-BP 算法和LA-VB 算法所成圖像受噪點影響嚴(yán)重,導(dǎo)致機尾處部分結(jié)構(gòu)特征缺失;本文的BI-FF SBL 算法所成圖像中雖然存在少量噪點,但依然能較好地體現(xiàn)飛機結(jié)構(gòu)特征。
信噪比為5 dB 時,4 種算法的ISAR 成像效果都有所提高,L1-BP 算法和LA-VB 算法均好于R-D算法。BI-FF SBL 算法效果最好,圖像中只有少量噪點且飛機結(jié)構(gòu)特征清晰。
在信噪比為10 dB 時,4 種算法都能給出清晰的ISAR 圖像,但3 種超分辨率算法的分辨率明顯高于R-D 算法。在L1-BP 算法和LA-VB 算法結(jié)果中,均存在較明顯的條紋干擾,而BI-FF SBL 算法則很好地去除了條紋干擾,在提高分辨率的同時很好地保留了飛機的幾何結(jié)構(gòu)特征。
3.3 圖像重構(gòu)誤差實驗
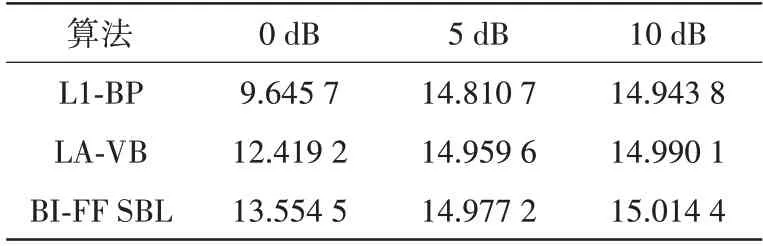
傳統(tǒng)ISAR 成像算法,如R-D 算法和MUSIC 算法等,其回波數(shù)據(jù)的尺寸和ISAR 成像的尺寸是一致的,即M=P,N=Q。在超分辨ISAR 成像中,ISAR成像的尺寸可以遠(yuǎn)大于回波數(shù)據(jù)的尺寸,即M 本文采用重構(gòu)信噪比(Reconstruction Signal to Noise Ratio,RSNR)作為指標(biāo),來評價超分辨ISAR成像算法的重構(gòu)誤差,其定義如下: 在該實驗中,以A-10 攻擊機為ISAR 成像目標(biāo),通過高頻電磁仿真得到相關(guān)回波信號。然后向回波信號中添加高斯白噪聲,得到信噪比分別為0,5 和10 dB 的實驗數(shù)據(jù)。該實驗對比了BI-FF SBL 算法、L1-BP 算法和LA-VB 算法的RSNR,對比結(jié)果如表1所示。對于其中每一種算法,在獲取原尺寸圖像W時,M=N=256,P=Q=256;在獲取超分辨圖像?時,M=N=128,P=Q=256。 表1 不同超分辨ISAR成像算法的RSNR對比 由表1可知,3種超分辨ISAR 成像算法在實驗數(shù)據(jù)信噪比由5 dB降為0 dB時,RSNR 都有明顯的下降,其中L1-BP算法最為明顯,RSNR下降至10 dB以下。BI-FF SBL 算法在信噪比為10 dB 時,RSNR可以達(dá)到15.01 dB,且在信噪比下降至0 dB 時,RSNR 依舊可以保持在13 dB 以上。由此可見BIFF SBL算法的重構(gòu)誤差明顯低于L1-BP算法和LAVB算法。 為了在ISAR 成像中更好地壓制噪聲,消除條紋干擾,提高成像分辨率,本文提出一種基于雙向插值處理和頻域信息融合的稀疏貝葉斯學(xué)習(xí)算法,即BI-FF SBL 算法。為了驗證BI-FF SBL 算法的效果,本文進(jìn)行了基于仿真數(shù)據(jù)和實測數(shù)據(jù)的ISAR 成像實驗,并將實驗結(jié)果與其他3 種ISAR 成像算法進(jìn)行對比,發(fā)現(xiàn)BI-FF SBL 算法在壓制噪聲和去除條紋干擾方面具有明顯的優(yōu)勢,且能提供更高的ISAR 成像分辨率。重構(gòu)誤差實驗結(jié)果表明,相比于其他兩種超分辨ISAR 成像算法,BI-FF SBL算法的重構(gòu)誤差更低。 本文BI-FF SBL 算法的不足是需要更多的計算時間。跟利用EM 算法進(jìn)行參數(shù)重構(gòu)的傳統(tǒng)SBL 算法相比,LA-VB 算法在參數(shù)重構(gòu)時,需要計算高斯一階絕對矩,其中包括多次計算庫默爾函數(shù),導(dǎo)致運算量增加。本文的BI-FF SBL 算法為了增強壓制噪聲的能力,進(jìn)行了兩次插值預(yù)處理,再基于LA-VB 算法進(jìn)行兩次參數(shù)重構(gòu),導(dǎo)致計算時間增加。后續(xù)工作將探索計算復(fù)雜度更低的ISAR成像算法,在保留ISAR 成像效果的同時力求降低運算時間。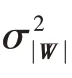
4 結(jié)束語

