考慮殘余變形的SMA棒材數值模擬方法研究

俞昊然, 李維濱

(1.南通四建集團有限公司,江蘇 南通 226300;2.東南大學 土木工程學院,南京 211189)

形狀記憶合金(shape memory alloy,SMA)是一種新型功能材料,具有獨特的形狀記憶效應、超彈性、高阻尼性、耐磨性以及良好的生物相容性,已經被廣泛應用于土木工程、生物醫學、航空航天等領域[1]。SMA具有兩種主要金相,分別為低溫穩定的馬氏體相和高溫穩定的奧氏體相,通過改變溫度和應力均能夠使得SMA發生馬氏體與奧氏體之間的可逆相變。在無應力狀態下,SMA的相變特征溫度包括馬氏體相變開始溫度Ms、馬氏體相變結束溫度Mf、奧氏體相變開始溫度As、奧氏體相變結束溫度Af,且一般情況下MfAf,SMA處于完全奧氏體相,此時馬氏體正、逆相變可完全由應力誘發,材料表現出超彈性特征,外力卸載時通過逆相變驅動可使大應變瞬時自動恢復,并在加卸載循環中形成滯回環從而耗散能量;當T繼續增大,SMA材料則會表現出與普通金屬材料一致的彈塑性特征。

當SMA元件具有超彈性特征時,無需額外供熱供電即可實現瞬時自復位。應用較多的SMA基本元件有棒材[2]、絲材[3]、彈簧[4]、碟簧[5]、環簧[6]等,其中SMA棒材僅需在端部車削螺紋,搭配螺母便可進行有效固定,裝配簡便迅速,因此應用較為廣泛。許多國內外學者對不同直徑的超彈性SMA棒材進行了循環拉伸試驗,考察了材料的相變應力、殘余應變、耗能能力、變形能力等力學性能,并對SMA棒材的尺寸效應[7-8]、熱處理工藝[9-10]、加載速率[11-12]、循環次數[13-14]、應變幅值[15-17]、初始預應變[18]等影響因素進行了研究。研究結果表明,經過合適的熱處理作用,SMA棒材可以具有良好的超彈性、延性、承載力和阻尼性能。然而,不同直徑的SMA棒材所需的最佳熱處理溫度和時間各不相同,且熱處理方式、材料組成、應變幅值等因素對棒材的殘余變形影響很大,這就使得在實際應用中未經過拉伸訓練的SMA棒材很難達到完全理想情況下的超彈性。表1列出了已有研究中關于SMA棒材拉伸試驗的殘余應變結果,可以看到經過適當熱處理后的SMA棒材在拉伸過程中仍有可能會出現一定程度的殘余變形。

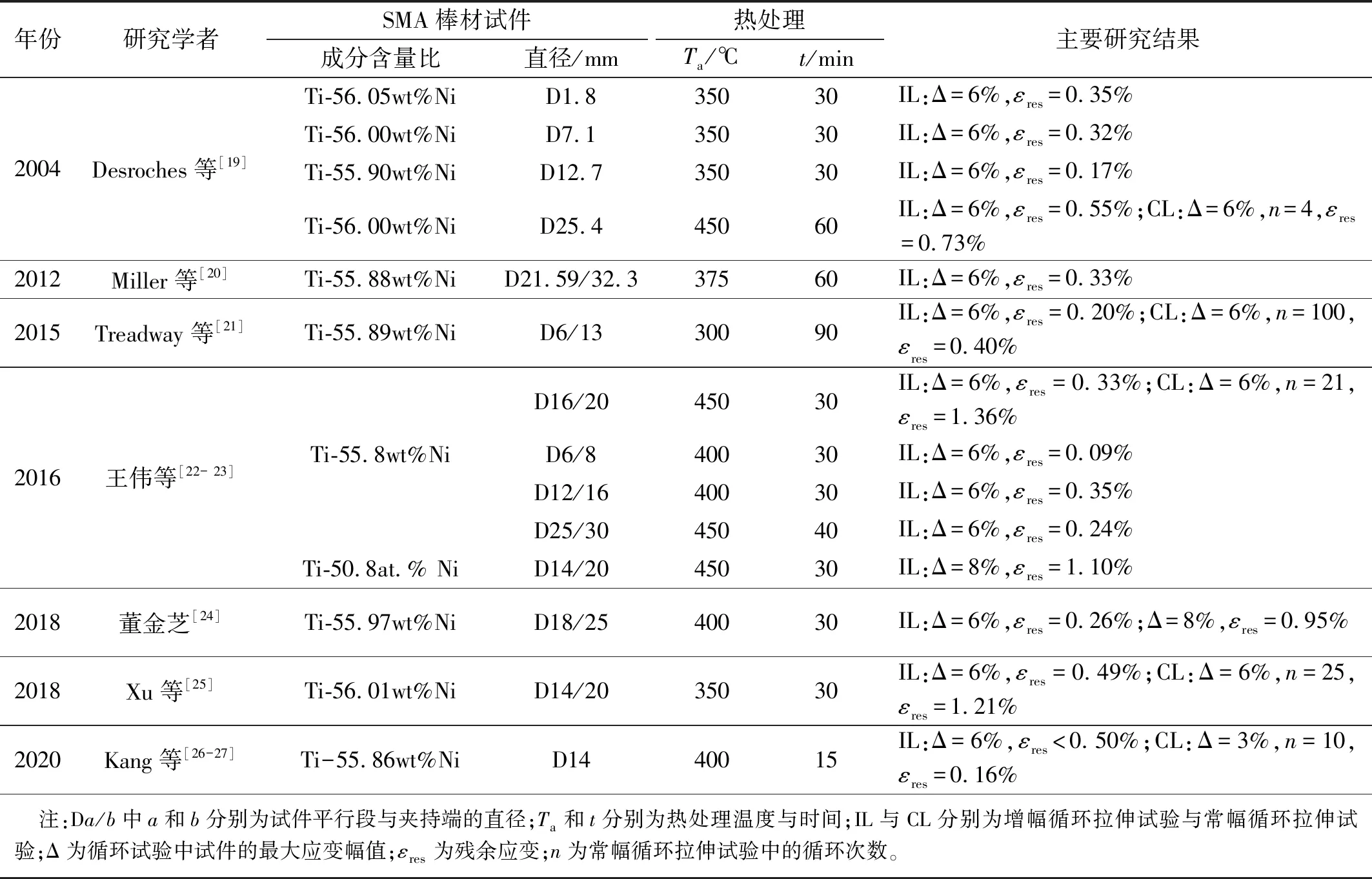
表1 SMA棒材拉伸試驗殘余應變結果匯總

由于SMA棒材自身兼具獨特的超彈性和高阻尼特性,在材料層次便能夠實現自復位和耗能的防震機制,近年來,可恢復功能抗震研究領域的一大亮點便是將SMA棒材應用于自復位結構體系,例如采用SMA棒材連接的自復位梁柱節點[28-31]、搖擺柱[32-33]、自復位剪力墻[34]、自復位耗能阻尼器[35-37]等。國內外科研人員通常采用試驗與數值模擬的方法對所設計的SMA自復位結構進行抗震性能研究,然而對于結構中SMA棒材的數值模擬,無論是通過桿系簡化模型還是采用精細化實體單元的方式,模擬時大多是基于理想的超彈性本構模型,未考慮SMA棒材在循環拉伸中出現的殘余應變,因此理論上無法準確考察整體結構在實際情況下的殘余變形,反映出的結構自復位性能也是偏于理想的。本文采用Auricchio唯象理論本構模型對4個循環拉伸試驗中的超彈性SMA棒材試件進行了精細化有限元模擬,在此基礎上提出一種可以反映殘余變形的SMA棒材有限元模擬方法,并將采用該模擬方法計算得到的算例結果與試驗數據進行對比驗證。

1 SMA材料性能參數

圖1反映了超彈性SMA棒材在循環拉伸過程中的一個滯回循環。σMs,σMf,σAs,σAf分別為馬氏體相變開始應力、馬氏體相變結束應力、奧氏體相變開始應力、奧氏體相變結束應力;εMs,εMf,εAs,εAf分別為馬氏體相變開始點、馬氏體相變結束點、奧氏體相變開始點、奧氏體相變結束點對應的應變;σu與εu分別為循環拉伸中材料的極限抗拉強度與最大應變;εres為SMA材料在循環結束時的殘余應變,其大小等于F點的應變值;ε0為循環起始點的應變,即上一次循環結束時的殘余應變;εL為材料的最大可恢復應變,其大小等于F點與G點的應變值之差;EA,EM分別為奧氏體彈性模量與馬氏體彈性模量;曲線SABCDEFS所圍面積為SMA材料在單次循環中的耗能密度ΔW,試驗中所有循環的累積總滯回耗能密度用W表示。

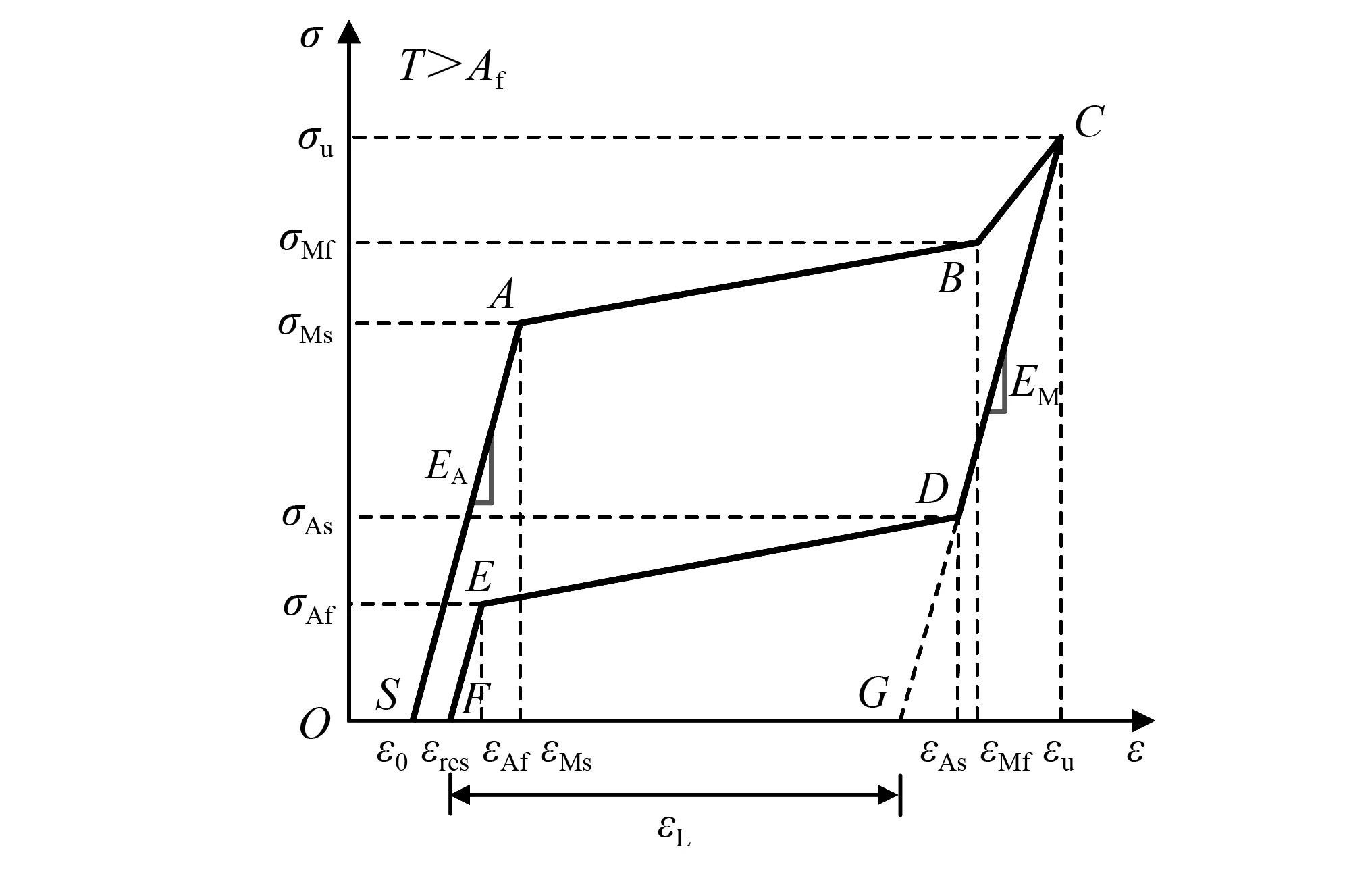
圖1 循環拉伸作用下超彈性SMA棒材的應力-應變曲線

2 SMA棒材增幅循環拉伸試驗

2.1 SMA棒材試件

熱軋態SMA棒材成分原子含量比為Ti-50.8at.%Ni,標定的奧氏體相變結束溫度Af約為0℃,即材料在一般室溫下處于奧氏體相態。SMA棒材試件根據GB/T 228.1—2021《金屬材料拉伸試驗》[38]的規定設計為狗骨形圓棒,平行段直徑為16.3 mm,夾持端直徑為24 mm,原始標距為81.5 mm,平行段長度為90 mm,過渡段半徑為21 mm,試件總長為194 mm,幾何尺寸如圖2所示。

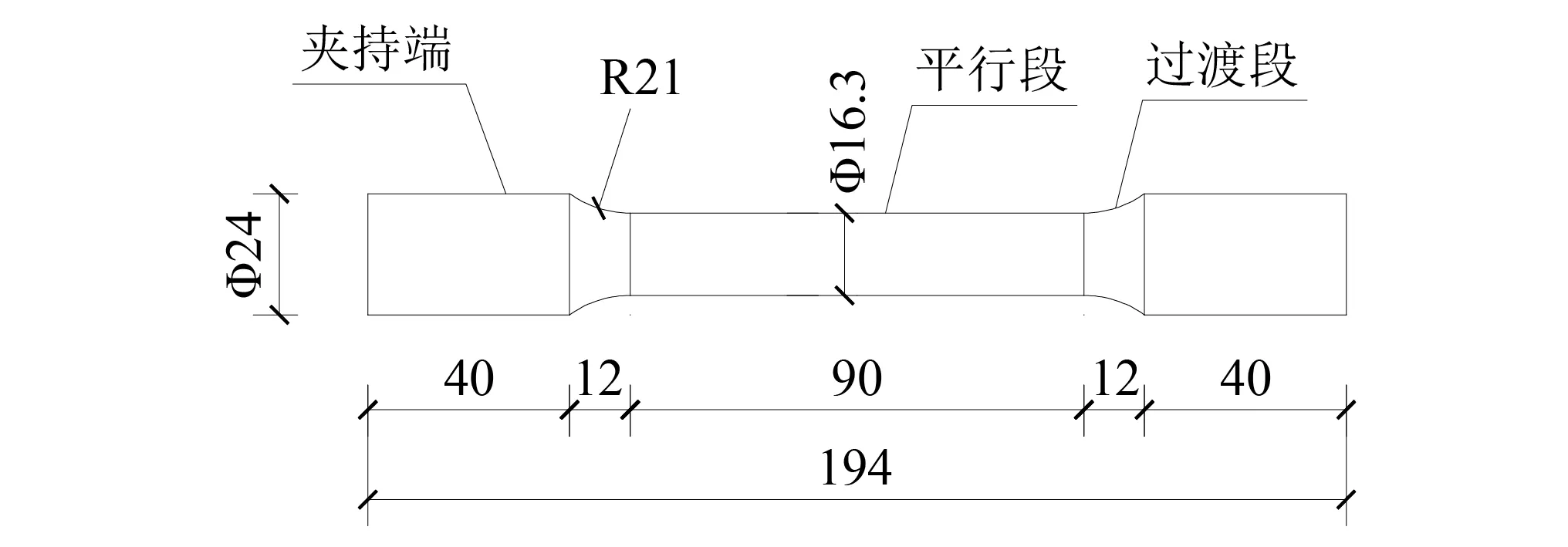
圖2 SMA棒材試件幾何尺寸(mm)

超彈性SMA棒材的制備需要經過車削加工和熱處理兩個流程。原始SMA熱軋圓棒于工廠車間內通過車削和打磨拋光形成狗骨形棒材,需要注意的是,所購SMA熱軋圓棒的直徑應略大于24 mm,從而為后期車削設置一定的加工冗余度。熱處理是指材料在固態下,通過加熱、保溫和冷卻的手段,以獲得預期組織和性能的一種金屬熱加工工藝,經過合適的熱處理后SMA棒材的力學性能及超彈性會進一步提升且更加穩定。需要說明的是,對SMA棒材進行熱處理宜設置于車削加工之后,此做法主要有以下三個方面的原因:①試件車削后易產生加工殘余應力,通過后續的熱處理可降低或消除此殘余應力,有研究表明,熱處理在車削之后進行,SMA棒材的殘余變形更小,力學性能更優[20];②車削后的試件呈狗骨形,平行段的直徑縮小,當進行熱處理時該部位在截面尺度上內外受熱更加均勻,減少了尺寸效應對試件熱處理效果的影響;③根據研究發現,經過中溫時效處理后的SMA棒材會變得愈加堅硬[39],車削的難度和成本會增大很多。

熱處理過程中,溫度和時間這兩個參數的設定與試件的尺寸有關,理論上不同截面尺寸的SMA棒材都對應著特定的最佳熱處理溫度與時間。參考表1中已有關于SMA棒材最佳熱處理溫度與時間的研究,試驗對4根SMA棒材試件設置了不同的熱處理溫度Ta,分別為350 ℃,400 ℃,450 ℃,500 ℃,熱處理時間t均為30min,試件的編號及熱處理參數如表2所示。采用管式電爐進行熱處理,具體做法是先將爐內加熱到合適的溫度,隨后將SMA試件置入爐內進行時效處理,保溫結束后取出棒材使其在空氣中自然冷卻,熱處理后的試件成品如圖3所示。

圖3 熱處理后的SMA棒材試件

表2 SMA棒材試件種類及熱處理參數

2.2 試驗裝置及加載制度

采用電子萬能試驗機進行試驗加載,試驗機所能提供的最大力為300 kN,荷載大小采用試驗機內置傳感器測量并由計算機自動采集,試件由試驗機兩端的楔形機械夾頭夾緊,采用標距為50 mm、量程為10 mm(20%)的YYU-10/50型引伸計測量該標距內的長度變化,試驗裝置如圖4所示。試驗時的環境溫度為25 ℃,符合拉伸試驗的室溫要求(10～35 ℃)。

圖4 試驗裝置

試驗加載中應變幅值為0.5%,1%,2%,3%,4%,5%,6%,每級各循環一圈。加載時的速率采用引伸計位移控制,應變速率為0.000 32 s-1,每次循環加載至位移幅值的終止條件按引伸計測量控制。卸載時采用應力控制,速率為10 MPa/s,為保護試驗儀器,每次循環卸載至5 MPa結束。試驗的加載制度如圖5所示,需要說明的是,圖中的加載制度曲線是以理想超彈性體試件標距內的應變循環進行表示,實際情況下試件在每次循環結束時可能會出現一定大小的殘余應變。

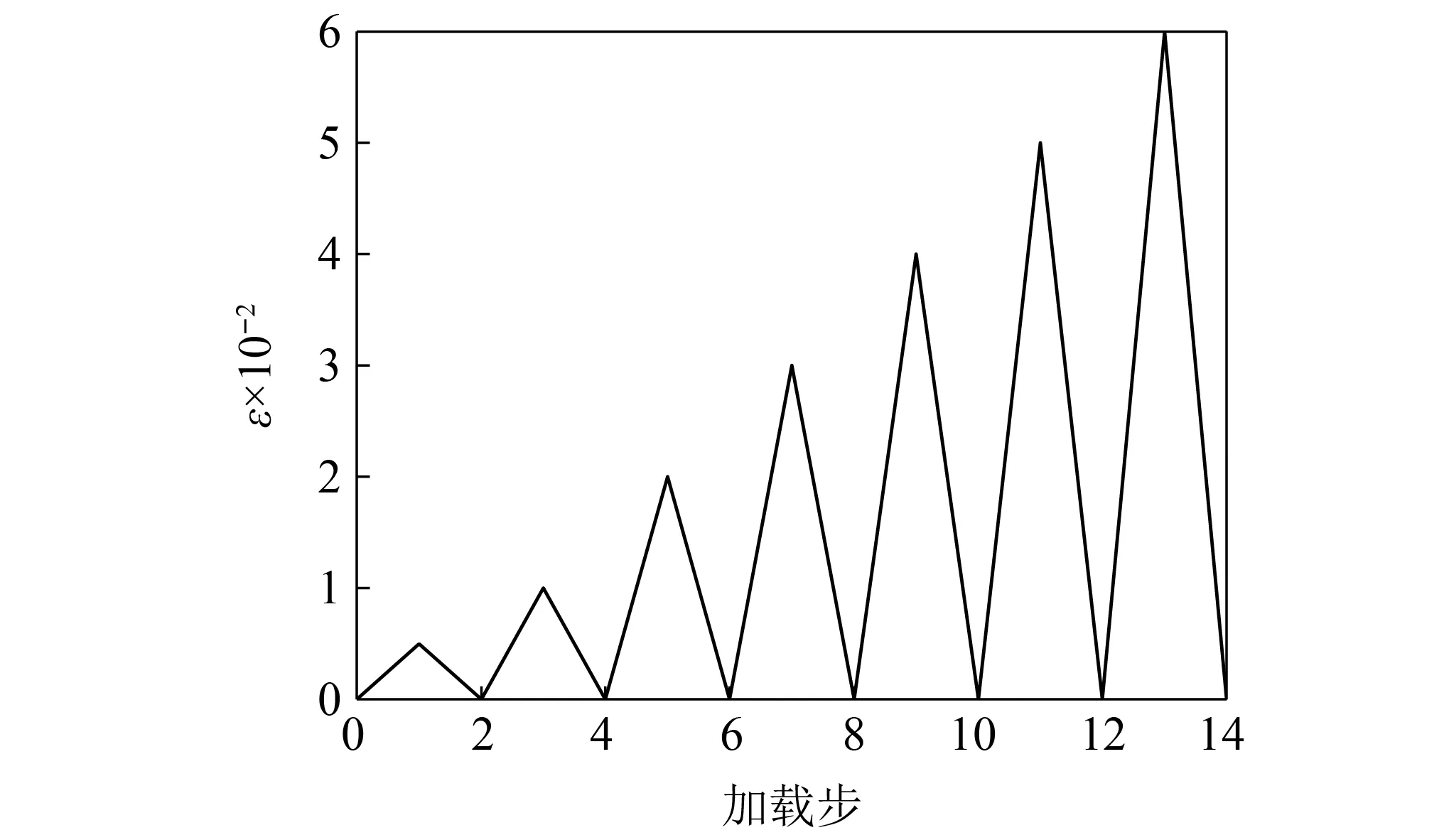
圖5 加載制度

2.3 試驗結果

各試件的應力-應變曲線如圖6所示。由圖6可以看出,不同的熱處理溫度對SMA試件的滯回曲線形狀、殘余應變、相變平臺高度、材料強度退化等力學性能影響很大。試件HT400與試件HT450的應力-應變曲線均呈現典型的旗幟形,馬氏體相變平臺清晰、平緩,且在試驗循環過程中下降幅度總體較小,表明材料的強度退化程度不大,當循環中的應變幅值較大時SMA材料還出現了馬氏體強化效應。

圖6 SMA棒材試件的應力-應變曲線

由圖6(c)可以明顯看到,試件HT450在第一圈循環加載初期,SMA材料由于R相變的影響出現明顯的非線性行為,產生了較大的殘余應變,但在試驗中后期的循環拉伸中則表現出良好的自復位性能。試驗結束時,試件HT450與試件HT400的殘余應變均很小未超過0.5%,可恢復應變較大,由此可知,當熱處理溫度為400 ℃和450 ℃、時間為30 min時,所研究的SMA棒材試件具有較好的超彈性特性。

3 超彈性SMA棒材數值模擬

3.1 有限元建模方法

有限元模擬選取上述試驗中超彈性較好的SMA棒材試件HT400與試件HT450進行研究,除此之外,還根據Andani等[40]和Li等[41]研究中的SMA棒材循環拉伸試驗進行有限元模擬及驗證。采用ABAQUS有限元軟件對各算例中的超彈性SMA棒材循環拉伸力學行為進行模擬。SMA本構模型選用Auricchio模型[42],該模型屬于描述材料宏觀行為的唯象理論本構模型,模型參數可根據SMA相變過程中的試驗曲線確定,模型引入的參數相對較少且形式簡單,能夠準確、方便地模擬材料的宏觀力學行為,在實際工程研究中應用較多。由于ABAQUS-2017的材料庫已經內置Auricchio超彈性本構模型,建模時僅需對SMA材料添加屬性即可,各算例建模所需的本構模型參數如表3所示。

表3 有限元模擬本構模型參數

建立SMA棒材有限元模型時將其一端固定,另一端設置一個參考點,作為控制點與加載端平面進行運動耦合,并施加沿桿軸方向的位移荷載,控制加載制度與試驗中的情況相同。模型單元采用三維實體單元C3D8R,該單元是一種8節點六面體線性減縮積分單元,它在彎曲荷載下不易發生剪切自鎖現象,計算結果具有較好的精確性,且由于采用了減縮積分,在計算效率上有較大優勢。網格劃分時,對棒材模型的過渡段與平行段適當加密,以試件HT400與試件HT450為例,圖7為SMA棒材網格劃分后的有限元模型。

圖7 SMA棒材有限元模型示意圖

3.2 模擬結果

圖8反映了各算例有限元模型的應力-應變曲線。由圖8可知,各超彈性SMA棒材模擬曲線的形狀均呈現典型的旗幟形,具有清晰的彈性段、相變平臺以及馬氏體強化階段,基本能夠反映試驗曲線的總體特征及大致變化。不過觀察各算例中的應力-應變模擬曲線可以發現,算例一的有限元模型在加載、卸載階段曲線吻合度均較好,而其余三個算例模型在不同應變幅值的循環中對于馬氏體逆相變階段的模擬效果相對欠佳,且對于馬氏體相變階段的強度退化特征也無法有效反映,這是因為試驗中SMA棒材試件的相變應力在不同應變幅值的循環下會發生變化,而有限元模擬時采用的是Auricchio唯象理論本構模型,該類模型適用于工程應用,其建模參數較少,形式簡單,參數設置時不考慮增幅循環拉伸過程中SMA試件相變應力的變化,由此可能會在模擬相變過程時產生一定的誤差;而算例一中的SMA棒材試件僅循環了一次,其模型參數僅需根據單次循環試驗結果進行設置,因此能夠與試驗曲線較好吻合。

圖8 各算例有限元模擬的應力-應變曲線

除此之外,還可以看到算例三中試件HT450的模擬曲線在彈性階段與試驗結果存在明顯偏差,這是由于有限元模擬不能反映試件HT450在試驗初期的R相變,這使得試驗曲線相比于模擬曲線整體向右偏移,且試驗曲線的有效最大應變幅值相對較小,導致模擬曲線在馬氏體強化階段的應力發展更為充分,極限抗拉強度相比試驗結果較大。

有限元模擬結果的關鍵性能指標總結于表4,其中各算例模型的奧氏體彈性模量EA、馬氏體相變開始應力σMs、極限抗拉強度σu均與試驗結果相差較小,而總滯回耗能密度W的誤差則相對較大,這主要是由于有限元模型的參數設置無法考慮到試驗中的相變應力變化,尤其是在模擬小變形循環的馬氏體逆相變時曲線較為飽滿。

表4 關鍵性能參數模擬結果

根據以上對SMA棒材的有限元模擬結果可知,各模型曲線基本能夠準確反映SMA材料在循環拉伸過程中的應力-應變關系及關鍵性能參數,然而觀察圖8中各算例的有限元模擬曲線也可以明顯發現,在每次循環卸載完成時曲線均回歸至坐標原點,即不能反映真實情況中SMA試件在循環拉伸作用下的殘余變形,因此以上對于SMA棒材的模擬研究結果是偏于理想的。

4 考慮殘余變形的SMA棒材數值模擬方法

4.1 模擬方法及理論推導

為了準確、簡便地模擬循環拉伸過程中SMA棒材的殘余應變,提出一種可以考慮殘余變形的SMA棒材有限元模擬方法,具體思路為:將SMA棒材有限元模型平行段中部的一段置換為具有相同截面和長度的殘余變形等效段,該等效段材料的性能類似于普通的彈塑性金屬,在彈性階段其應力-應變關系與SMA材料相同,而當拉伸時的最大應力超過自身的屈服應力并完全卸載后會出現一定程度的塑性變形,模擬時以該等效段產生的塑性變形來反映SMA棒材試件標距范圍內出現的殘余變形。圖9為考慮殘余變形的SMA棒材有限元模擬方法示意圖。其中:lg為棒材試件的標距;lSMA和leq分別為標距內的SMA段總長度和等效段長度;Δlg為拉伸時標距范圍內棒材的伸長長度;ΔlSMA和Δleq分別為拉伸時標距內的SMA段和等效段的伸長長度;εp為卸載后等效段材料的塑性應變;εres為標距內的殘余應變,即試驗測得的SMA棒材產生的殘余應變。

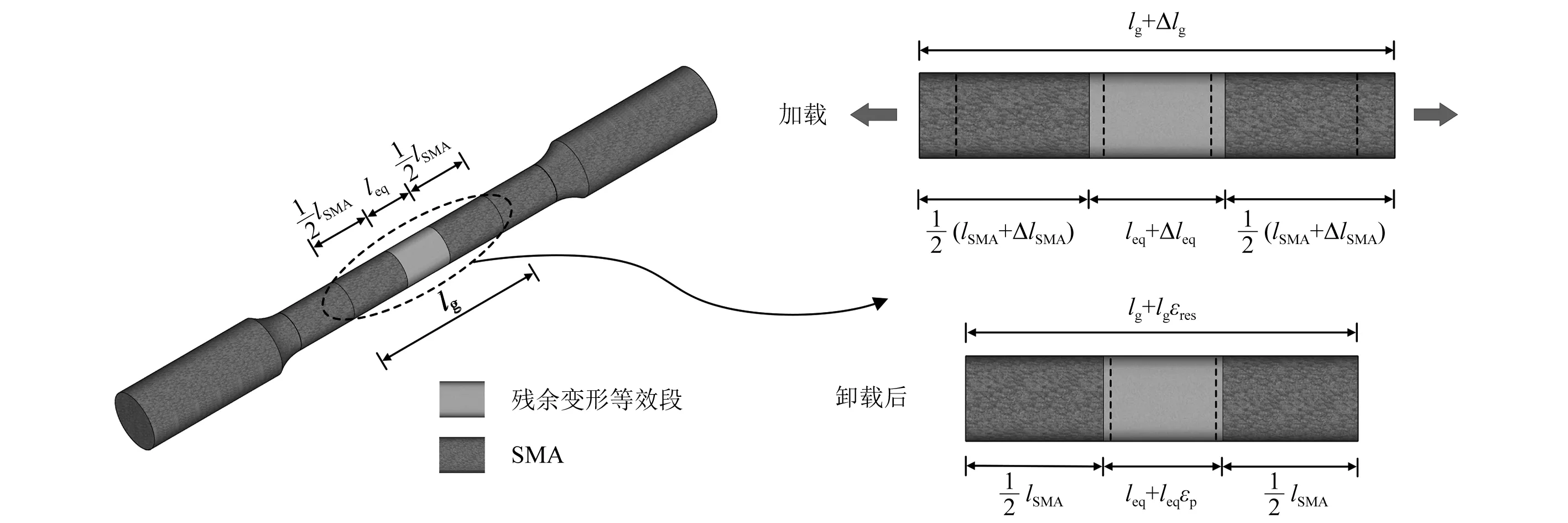
圖9 考慮殘余變形的SMA棒材有限元模擬方法示意圖

為保證加載階段等效材料的應力-應變關系與SMA材料接近,令等效材料的彈性模量E與SMA的奧氏體彈性模量EA相同,等效材料的屈服應力σeq,y與SMA的馬氏體相變開始應力σMs相同。等效段材料的軸向拉伸應力-應變關系采用多折線的形式進行表示,如圖10所示。其中:σeq,n和εeq,n分別為等效段材料在本構折線第n個拐點處的應力、應變,大小分別等于SMA材料在對應循環中位移幅值處的應力和應變(馬氏體相變開始點之后);εp,n為等效段材料在第n個拐點卸載完成后的塑性應變。此外,為了使等效段材料的塑性變形等于SMA棒材標距內的殘余變形,等效段的長度leq需要滿足一定要求,以下對該段長度取值進行推導求解。

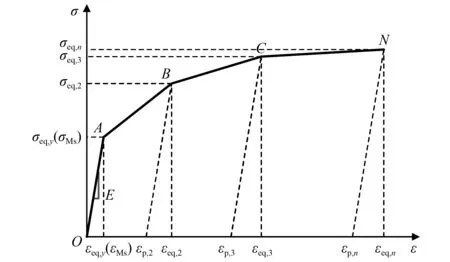
圖10 殘余變形等效段材料的應力-應變關系

由圖9可知,SMA棒材在拉伸過程中標距長度伸長Δlg可以表示為

Δlg=Δleq+ΔlSMA=leqεeq+lSMAεSMA

(1)

式中,εeq與εSMA分別為循環拉伸過程中試件標距內殘余變形等效段的應變和SMA段的應變。

初始狀態下,標距內SMA段的總長度lSMA可表示為

lSMA=lg-leq

(2)

將式(2)代入式(1)可得到

Δlg=leqεeq+(lg-leq)εSMA

(3)

由圖10可知,等效段材料在第n次循環中拉伸至位移幅值時的應變εeq,n為

(4)

在棒材試件的標距內,由于等效段截面與SMA段截面幾何相同,根據等應力原則可認為標距長度范圍內任一截面處應力σg均相同,即

σg=σeq=σSMA

(5)

由于在有限元模擬中SMA材料的本構模型為理想超彈性模型,模擬結果中不存在殘余變形,因此SMA棒材標距長度范圍內的實際殘余變形均由等效段材料的塑性變形代替,由此可知第n次循環結束后等效段的塑性應變εp,n應為

(6)

結合式(5)與式(6),式(4)可表示為

(7)

結合式(3)與式(7),第n次循環中棒材拉伸至位移幅值時標距長度范圍內的伸長Δlg,n可表示為

(8)

將式(8)進行變換,此時試件標距范圍內的任一截面應力σg,n可表示為

(9)

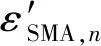
(10)

將式(10)代入式(9)可得

(11)

當原本的棒材有限元模型中某一段SMA材料被置換后,在滿足殘余應變等效要求的同時,還需使得等效材料替換后的SMA棒材應力-應變關系與原本材料情況相近。這里假設第n次循環中試件拉伸至最大位移時,含有等效材料的棒材標距范圍內SMA段的應力、應變與原本SMA棒材相同,即需滿足

(12)

(13)

將式(12)代入式(11)可得

(14)

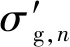
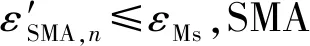
(15)

該情況下,式(15)滿足式(13)要求。

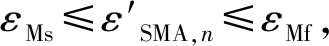
(16)

式中,EAM為SMA馬氏體正相變階段的加載剛度。

若要滿足式(13)要求,則需聯立式(16)與式(14),可以解得殘余變形等效段的長度leq為

(17)

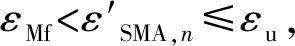
(18)

式中,RS為SMA馬氏體強化階段的加載剛度。

聯立式(18)與式(14),可以解得該情況下的殘余變形等效段長度leq為

(19)

值得注意的是,當需要模擬SMA棒材(螺桿)構件在實際應用中的殘余變形時,若平行段(工作段)較長且夾持端的截面尺寸相對較大,此時可忽略試件夾持端的伸長以及“邊界效應”對工作段端部應力的影響,根據循環中SMA最大幅值點的應力應變情況,將式(17)和式(19)中的標距長度lg替換為棒材的工作段長度lw即可。

4.2 模擬結果及驗證

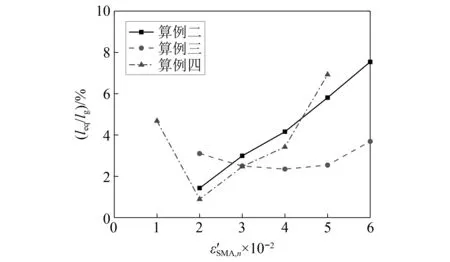
圖11 殘余變形等效段長度與試件標距比值

采用上述考慮殘余變形的SMA棒材模擬方法對原先的有限元模型進行改進,具體步驟是根據計算得到的等效段長度leq對SMA棒材模型的平行段進行分割,隨后采用圖10中的本構關系對等效段的材料屬性參數進行設定,其余的建模方法及本構模型參數均不作改變,模擬結果如圖12所示。由圖12可以看到,考慮殘余變形的有限元模型可以有效地反映SMA棒材試件在加卸載循環中殘余應變的產生,且模擬曲線與試驗曲線的形狀也較為吻合。

圖12 考慮殘余變形的有限元模擬曲線及對比

考慮殘余變形的有限元模擬結果主要性能參數如表5所示。由表5可以看出,除了算例三中試件HT450由于R相變的影響使得試驗結果與有限元模擬的殘余應變有一定偏差外,其余算例情況下基本能夠準確地反映出試件在試驗結束時的殘余應變大小,且對比其他性能參數可知,考慮殘余變形的有限元模型能夠較為準確地表現試件的各項基本力學性能。

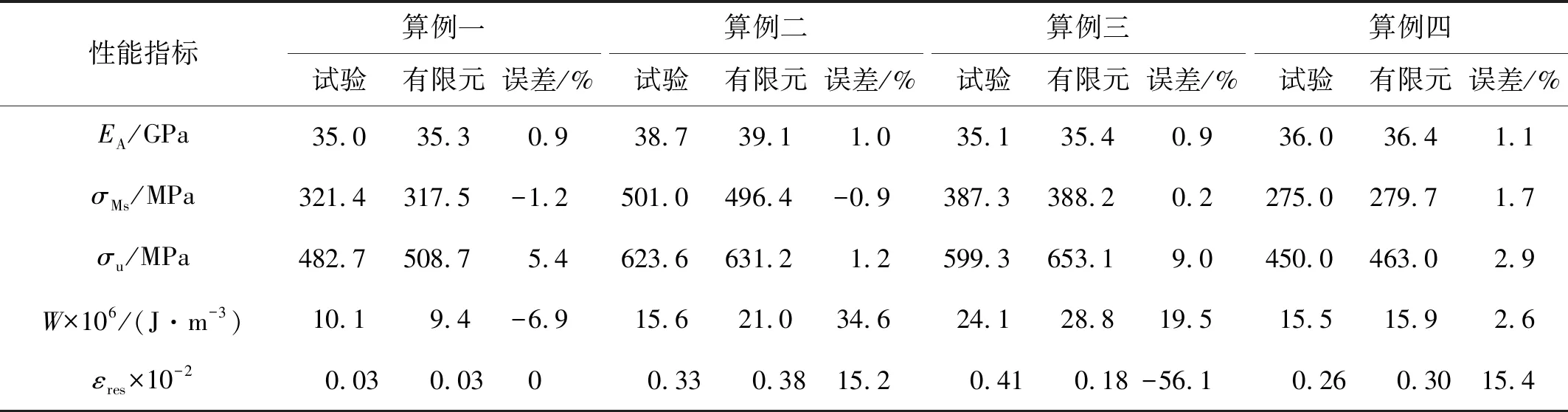
表5 考慮殘余變形的SMA棒材有限元模擬結果與試驗對比

圖13反映了算例二～算例四中有限元模型在每個循環結束后的殘余應變模擬結果。由圖13可以看到,雖然模型建立時材料等效段的長度是根據試驗中最大應變幅值對應的殘余應變確定的,但對于循環過程中不同應變幅值下的殘余應變模擬誤差也相對較小。此外,圖13(b)還比較了試件HT450在剔除R相變階段非線性影響后的殘余應變情況,可以總結出,當通過拉伸訓練或其他手段消除R相變的影響后,有限元模擬結果也能夠較好地反映各次循環中的殘余應變。

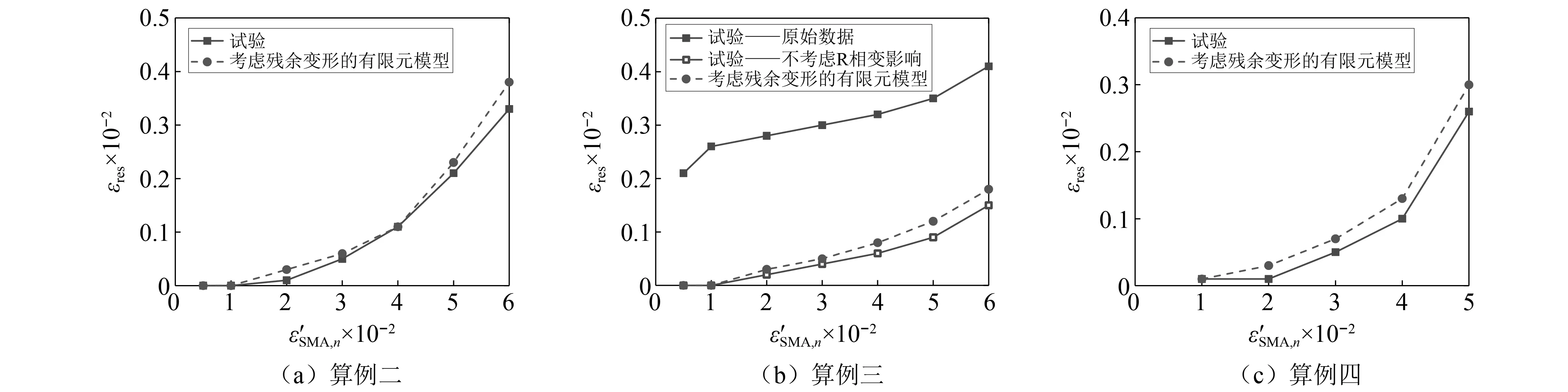
圖13 不同應變幅值下的殘余應變模擬結果對比

5 結 論

本文首先通過增幅循環拉伸試驗對經過不同熱處理作用的SMA棒材進行了超彈性性能考察,隨后采用Auricchio唯象理論本構模型對4個超彈性SMA棒材算例進行了有限元模擬,在此基礎上,提出了一種可以考慮殘余變形的SMA棒材有限元模擬方法,并給出了具體的理論推導,最后根據試驗數據對模擬結果進行了驗證。研究結論如下:

(1)對于所研究的平行段直徑為16.3 mm的SMA(Ti-50.8at.%Ni)棒材而言,溫度范圍為400～450 ℃、時間為30 min的熱處理作用能夠使其獲得良好的超彈性。

(2)本文提出的可以考慮殘余變形的SMA棒材有限元模擬方法,采用了材料置換的思路,以等效彈塑性金屬的塑性變形來反映SMA棒材受力后的殘余變形,經試驗驗證其能夠準確地模擬SMA棒材包括殘余變形在內的各項力學性能。