分接開關快速機構時變運動可靠性與靈敏度分析

段金燕,趙強強,汪可,李戈琦,張進華,洪軍

(1. 西安交通大學機械工程學院,710049,西安; 2. 西安交通大學現代設計及轉子軸承系統教育部重點實驗室,710049,西安; 3. 中國電力科學研究院有限公司,100192,北京)

快速機構是特高壓換流變有載分接開關的關鍵部件之一,通過能量的儲存與釋放,帶動有載分接開關運動,從而使換流變閥側電壓在網側電壓產生波動時保持穩定,實現不停電、帶負載調節[1-2]。由于存在零件加工與裝配誤差的不確定性,快速機構在能量的儲存與釋放過程中不可避免地會出現失效。儲能過程是釋能過程順利完成的前提,為保障有載分接開關實現功能切換,避免產生上百千安的電弧放電或起火爆炸問題,要求快速機構在整個儲能過程中運動可靠,即其運動誤差在整個儲能過程中應處于安全范圍。因此,從保障特高壓電網安全運行的角度出發,開展分接開關快速機構運動的可靠性分析至關重要。

根據所涉及的時間長度,將可靠性分析分為非時變可靠性與時變可靠性[3-5]2種類型。非時變可靠性又稱點可靠性,指的是在某一個時間點上極限狀態函數處于安全區域的概率,不受前面時刻運動失效的影響;而時變可靠性評估的是整個時間段上的可靠程度,受前面時刻失效的影響,即只要在這段時間上出現失效,則整個時間段上失效。上述分類同樣適用于運動可靠性。考慮到有載分接開關重點關注的是快速機構在整個儲能過程中的運動可靠性,但傳統機構的運動可靠性大多集中于點可靠性,而時變運動可靠性分析能為工程設計階段提供更為客觀的服役性能評估,則僅考慮單個時刻點快速機構運行是否可靠已無法滿足設計需求。因此,進行機構時變運動可靠性分析,針對有載分接開關快速機構運動機制確定運動失效的影響因素,探討構件在整個運動區間內是否可靠,進而分析儲能過程中構件實現預期運動軌跡的可靠度,具有重要的工程意義。

目前,針對有載分接開關可靠性的研究,大多集中于開關使用過程中的故障診斷與故障預測。Seo等[6]為避免噪聲的耦合干擾,采用概率小波變換方法提取電弧信號,研制出一種電弧信號與振動數據相集成的狀態監測系統,并對2種不同類型的有載分接開關實現了現場在線監測。王豐華等[7]根據有載分接開關切換時的振動信號特征,將貝葉斯估計與支持向量數據方法相結合,建立了機械故障診斷模型,并對某CM型有載分接開關在正常工作與發生故障時的狀態進行有效識別。劉志遠等[8]提出一種有載分接開關彈簧儲能故障的識別方法,構建了神經網絡響應面模型,并與有限元仿真結果進行比較,實現了不同激勵力下故障特征的有效檢測。李小雙[9]對有載分接開關常見機械故障的類型和原因進行了分析,開發出多信號融合的機械故障診斷平臺,利用萬有引力搜索(GSA)優化算法對快速機構開展了故障診斷并具有較好的效果。金雷等[10]結合近年來真空有載分接開關發生的典型故障案例,分析了故障產生的原因,從多角度闡述了保證開關可靠運行的詳細舉措。毋庸置疑,運行階段的故障診斷與預測對于有載分接開關可靠性保障具有重要意義,但遺憾的是,上述方法均不能應用于有載分接開關的時變運動可靠性分析。

本文結合分接開關快速機構的運動機制,研究了其運動失效影響因素,通過構建時變運動可靠性分析模型,提出了一種新的首次穿越率解析求解方法,并基于此求解方法得到了快速機構時變運動失效概率序列。與蒙特卡羅方法相比,該方法在計算效率方面具有明顯的優勢。最后,根據該方法進行了靈敏度分析,研究變量的分布參數對時變運動可靠性的影響程度,從而為分接開關快速機構可靠性分析的評估與參數優化設計提供支撐。

1 快速機構運動分析

快速機構組成構件示意圖如圖1所示[11],主要包括偏心凸輪、擺桿、齒輪1、撥釘、儲能彈簧、拉桿、齒輪2和齒輪3。在儲能過程中,偏心凸輪在電機輸出轉矩的驅動下,帶動與其相配合的擺桿繞定軸擺動,擺桿在擺動過程中推動固連在齒輪1上方的撥釘運動,從而實現齒輪1繞中心軸順時針轉動,與齒輪1外嚙合的齒輪2作反方向逆時針轉動,此時,一端固接在齒輪2上的連桿被拉長,儲能彈簧緩慢壓縮并儲存能量;當彈簧經過死點位置時,在儲存能量的作用下會發生快速回彈,推動齒輪3轉動,從而帶動底層凸輪機構作90°轉動,完成釋能動作,此即釋能過程。

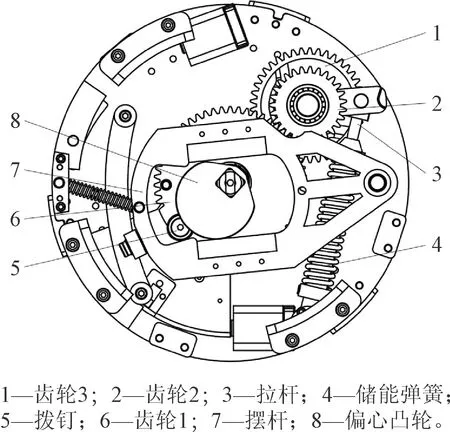
圖1 快速機構組成構件示意圖Fig.1 Components and motion analysis of quick mechanism

圖2 儲能彈簧形變量與力矩差值隨時間的變化曲線Fig.2 Deformation and torque variations of energy storage spring with time

在實際工程中,由于不確定性因素的存在,快速機構不可避免地會存在運動誤差[12-14]。圖2給出了儲能過程中,儲能彈簧在理想狀態下形變量的變化曲線,以及理想與實際狀態下齒輪2所受彈簧力矩的差值。結合圖1可知,理想狀態下偏心凸輪的回轉運動帶動擺桿進行往復擺動,導致拉桿伸長,儲能彈簧被壓縮,滿足規定的形變量條件,所受載荷沿軸心線方向。若拉桿的運動精度未達到預期要求,儲能過程在規定時間段內出現運動偏差,當偏差超出一定范圍后,一旦彈簧形變扭曲而引起貯存的能量不足或冗余,有載分接開關動作就會發生故障,嚴重時還會造成機構卡滯、拒動等,進而影響整個產品性能。因此,結合快速機構運動機制,對儲能過程進行失效模式影響因素分析,研究其在整個運動時段上的可靠性具有十分重要的意義。

2 快速機構運動失效影響因素分析

如上所述,在機構運動可靠性分析中,一般存在非時變運動可靠性與時變運動可靠性兩種情況。對于快速機構而言,由于要保障整個儲能過程的可靠運動,因此開展時變運動可靠性分析更為重要,分析結果亦更為保守。進行時變運動可靠性分析的第一步是構建機構運動輸入與輸出間的關系,表示如下

ψ(θ,λ,X)=0

(1)

式中:ψ為獨立運動方程;θ為機構輸入角度;λ為機構輸出角度;X為機構結構件參數。研究結構件參數即運動失效影響因素很有必要,因此,本文首先分析了快速機構的失效影響因素,為之后時變運動可靠性的分析提供數據基礎。

2.1 關鍵構件磨損影響分析

結合圖1中的快速機構二維示意圖,可知在單次運動過程中,撥釘與偏心凸輪始終和擺桿保持接觸狀態,不可避免地會產生因機械運動而造成的磨損,因此接觸碰撞所引起的構件磨損是快速機構運動失效的影響因素之一。本文所設計的撥釘與偏心凸輪的材料均為45鋼,撥釘外徑為30 mm,偏心凸輪偏心圓半徑為44.5 mm。

如圖3所示,從同批次樣機中隨機抽取3臺,選取45 000次切換運動為試驗步長開展切換試驗。對試驗采集到的撥釘外徑數據進行多項式擬合,擬合后的曲線繪制于圖4。

圖3 快速機構樣機切換試驗Fig.3 Prototypical experiment of quick mechanism

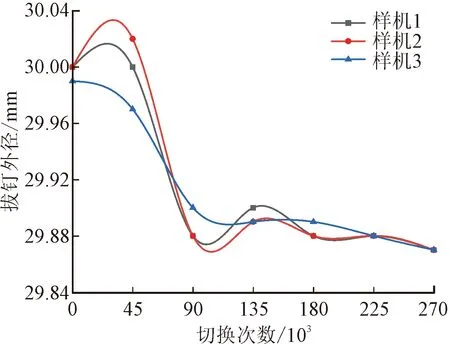
圖4 快速機構撥釘外徑擬合曲線Fig.4 Fitting curve of pin outer diameter of quick mechanism

對圖4數據進行分析可知,在允許測量誤差的情況下,當切換次數達到270 000次時,撥釘外徑的最大磨損量僅為0.13 mm。由此可知,當快速機構在整個儲能過程中單次運動時,快速機構的撥釘外徑變化較小。由試驗還可得到,偏心凸輪的磨損量在整個運動過程中變化緩慢。綜上可知,由于關鍵構件的磨損對于快速機構單次運動可靠性影響很小,因此本文在進行時變運動可靠性建模時,可不考慮磨損的影響。

2.2 加工與裝配誤差影響分析

在快速機構加工裝配過程中,針對同一批次零部件,構件尺寸可看作是服從正態分布的獨立隨機變量。下面,本文分析了此類不確定因素造成的隨機誤差對快速機構運動特性的影響。

采用機構等效替代方法,繪制快速機構運動學簡圖,如圖5所示。利用快速機構儲能過程的平面機構運動方程,基于矢量環方法構建運動誤差函數,分別建立了封閉環路AEDCB與AHGB的機構矢量運動方程。

圖5 快速機構運動學簡圖Fig.5 Kinematical diagram of quick mechanism

對于圖5中的封閉環路AEDCB,得到機構水平方向與豎直方向的運動方程分別為

(2)

式中:l1、l2、l3、lCD和l4分別為桿AB、AE、ED、DC、CB的長度;a為∠BCD的角度;θ為桿AE的輸入角度,即機構輸入角度,則封閉環路AEDCB的輸出角度λ1,即∠ABC,可表示為λ1(θ)。

將式(2)整理后,得到運動輸入與輸出之間的關系為

l2sin(a+θ+λ1)-l3+l4sina=l1sin(a+λ1)

(3)

同理,對于圖5中的封閉環路AHGB,可得機構的水平與豎直方向的矢量運動方程分別為

(4)

式中:l5、l6和lBG分別為桿AH、HG和GB的長度;b為∠CBG的角度;λ2為桿AH的輸出角度。將上式整理后,可得

-l1sin(λ1-b)+l5sin(λ1-b+λ2)+l6=0

(5)

至此,圖1中偏心凸輪、擺桿、撥釘、齒輪1傳動系統的運動輸入與輸出關系式構建完成。

圖6 齒輪系統偏心參數Fig.6 Parameters of eccentricity for gear system

對于齒輪系統運動精度,主要考慮其因零部件加工和裝配而造成的長周期誤差,包括幾何偏心和運動偏心[15-16]。如圖6所示,主動齒輪(直徑相對較大)與傳動齒輪的回轉中心分別為O′1、O2,假設主動齒輪運動時相對回轉中心存在一當量偏心O1O′1,其偏心距為d,此時主從齒輪相嚙合的點將不再在連心線上(見圖7),從動齒輪實際轉角與理論轉角間會產生運動誤差s,表達式可寫為

(6)

式中:αn是漸開線圓柱齒輪壓力角;γ是O1O′1與O1O2之間沿順時針方向的夾角,在 [0,2π]內服從均勻分布;d是幾何偏心和運動偏心的綜合,服從瑞利分布,可由齒輪切向綜合誤差F′i估計如下

(7)

其中F′i可參考國家標準GB/T 10095.1—2008。

(b)偏心齒輪副

在實際工程應用中,為了便于描述,一般將運動誤差s的線值轉化為角度值。對于圓柱直齒輪,運動誤差角度值φ與運動誤差線值s間的關系可寫為

(8)

式中:mn是從動齒輪法面模數;Z2是從動齒輪齒數。

考慮到γ在 [0,2π]內服從均勻分布,d服從瑞利分布,γ與d又相互獨立,因此有

(9)

(10)

式中:f(·)表示概率密度函數;σ表示正態分布的標準差。進而可得到

(11)

令l7=dsinγ,l8=dcosγ,則有

(12)

將式(12)代入式(11)進行換元,根據概率變換得到,l7、l8滿足l7～N(0,σ2)、l8～N(0,σ2),且l7與l8相互獨立。

因此,從動齒輪運動角可寫為

(13)

式中:λ20是桿AE與AB的初始夾角;Z1是主動齒輪齒數。

至此,快速機構在儲能過程中的構件輸入與輸出間關系已全部得到。

2.3 快速機構失效模式影響因素確定

一般地,對于一個確定構型的輸出機構,實際運動輸出為λ(X,θ),理想運動輸出為λ*(θ),則實際輸出與理想輸出之間的運動誤差函數可寫為

g(X,θ)=λ(X,θ)-λ*(θ)

(14)

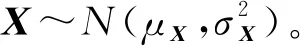
3 快速機構時變運動可靠性分析

對于時變可靠性,主要的分析方法包括蒙特卡羅法、極值分布法、代理模型法和首次穿越法等[17-20]。考慮到首次穿越法可實現時變可靠性的半解析求解,且能夠在單次計算中給出時變失效概率序列,因此本文采用首次穿越率法開展分析。

假設不同時刻的穿越事件是相互獨立的隨機過程,則在 [t0,tf]時間段內從安全域到失效域的穿越次數服從泊松分布[21-22]。考慮到θ=ωt,其中角速度ω為機構輸入角速度,則時變運動失效概率可表示為

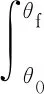
(15)

式中:v(θ)為首次穿越率,指的是單位時間內發生穿越事件的概率;θ0和θf分別為機構運動的初始與終止時刻;pR(θ0)為輸入為θ0時刻的非時變運動可靠性概率。

由式(15)可以看出,時變運動失效概率pF(θ0,θf)的求解依賴于首次穿越率v(θ)的計算。針對此問題,本文將采用一階線性展開對運動誤差極限狀態函數進行估計,并利用高斯截斷矩推導得到首次穿越率的解析解。

3.1 首次穿越率推導

首次穿越率是指單位時間內發生穿越事件(即穿越安全邊界)的概率。圖8給出了輸入為θ時刻,運動誤差極限狀態函數g(X,θ)穿越上安全邊界的示意圖,其中“×”表示穿越安全邊界,emax和emin分別為上安全邊界和下安全邊界的誤差值。

圖8 穿越事件示意圖Fig.8 Representation of the outcrossing event

首次穿越率的表達式可寫為

v(θ)=

v+(θ)+v-(θ)

(16)

式中:S是以emax和emin分別為上、下邊界的安全區間;v+(θ)為穿越上邊界的穿越率;v-(θ)為穿越下邊界的穿越率。本節只進行上邊界穿越率的求解,下邊界穿越率可用相同的方法推導得到。

為了簡化表達,假定式(16)中的g(X,θ)為變量ζ,g(X,θ+Δθ)為變量η,如圖9所示,則根據積分變換可得到穿越上邊界事件發生的概率為

Pr{g(X,θ)emax}=

(17)

式中:fg(X,θ),g(X,θ+Δθ)(ζ,η)為g(X,θ)和g(X,θ+Δθ)的聯合概率密度函數。

圖9 穿越上邊界事件發生概率積分變換示意圖Fig.9 Schematic diagram of probability integral transformation of events outcrossing the upper region

(18)

圖10 坐標轉化示意圖Fig.10 The diagram after the coordinate transformation

根據上述坐標變換,式(17)中穿越事件發生的概率可以改寫為

Pr{g(X,θ)emax}=

(19)

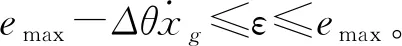
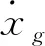
(20)

(21)

已知運動誤差極限狀態分布函數及其導數的聯合分布是二維高斯分布,其均值與協方差分別為μ1和Σ1,可得μ1=02×1,Σ1可從多維高斯分布協方差矩陣Σ中得到,表示如下

(22)

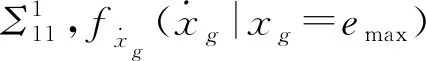
(23)

(24)

由此可得穿越上邊界的穿越率,表示如下

(25)

將式(25)后半部分定義為

(26)

(27)

式中:erf(·)是高斯誤差函數。

(28)

為了簡化表達,令

(29)

(30)

(31)

將式(31)代入式(25),可以得到穿越上邊界的穿越率

(32)

同理可得穿越下邊界的穿越率

(33)

將式(32)和(33)一同代入式(16),就可得到首次穿越率v(θ)的解析表達式。

3.2 快速機構運動可靠性

在極限狀態函數服從高斯分布的前提下,推導得到了首次穿越率的解析解,但實際上運動誤差極限狀態函數g(X,θ)并不能直接滿足這個條件。由于快速機構中各構件的名義尺寸遠遠大于其制造公差或裝配誤差,即尺寸變量的標準差σl遠小于其均值μl,故可將誤差函數g(X,θ)在均值μl處進行一階線性估計,將其從非高斯分布轉化為高斯分布,以滿足上述首次穿越率解析解的應用條件。

首先利用泰勒展開對g(X,θ)進行一階估計,得到

(34)

為簡化計算,令

li=μi+σiUi

(35)

式中:Ui～N(0,1)。

(36)

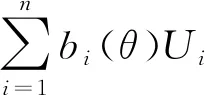
(37)

根據式(36)計算快速機構的隨機誤差,易得

b(θ) = [b1(θ),b2(θ),…,bn(θ)]

(38)

已知極限狀態函數g(X,θ)滿足式(14),由于機構的理想運動輸出λ*(θ)只與輸入的θ值有關,與構件的尺寸無關,則可通過

(39)

得到b(θ)的值。

(40)

(41)

式中:b′(θ)為b(θ)對θ的一階導數。

(42)

(43)

對于輸入為θ0時刻的非時變運動可靠性概率pR(θ0),可通過下式計算

pR(θ0)=Pr{emin≤g(X,θ0)≤emax}=

(44)

式中:Ф(·)是標準正態分布累積分布函數;μg(θ0)、σg(θ0)分別是運動誤差極限狀態函數在初始時刻的均值和標準差。

綜上所述,可先通過式(32)和(33)對快速機構誤差過程上、下穿越率進行求解,再由式(15)計算得到快速機構時變運動失效概率,具體過程總結如下。

步驟1確定運動誤差極限狀態函數g(X,θ),給定安全邊界S。

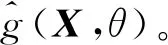
步驟3采用數值積分方法,由式(15)得到有載分接開關快速機構時變運動失效概率pF(θ0,θf)。

4 分析驗證

根據圖5中的封閉環路運動學模型,得到有載分接開關快速機構儲能過程的輸入角度θ,滿足θ∈ [105°, 205°],輸出角度為拉桿轉動角度λ,理想輸出角度為λ*。

根據工程經驗,快速機構中各構件的名義尺寸及參數如表1所示。其中,標準差為0表示固定值。

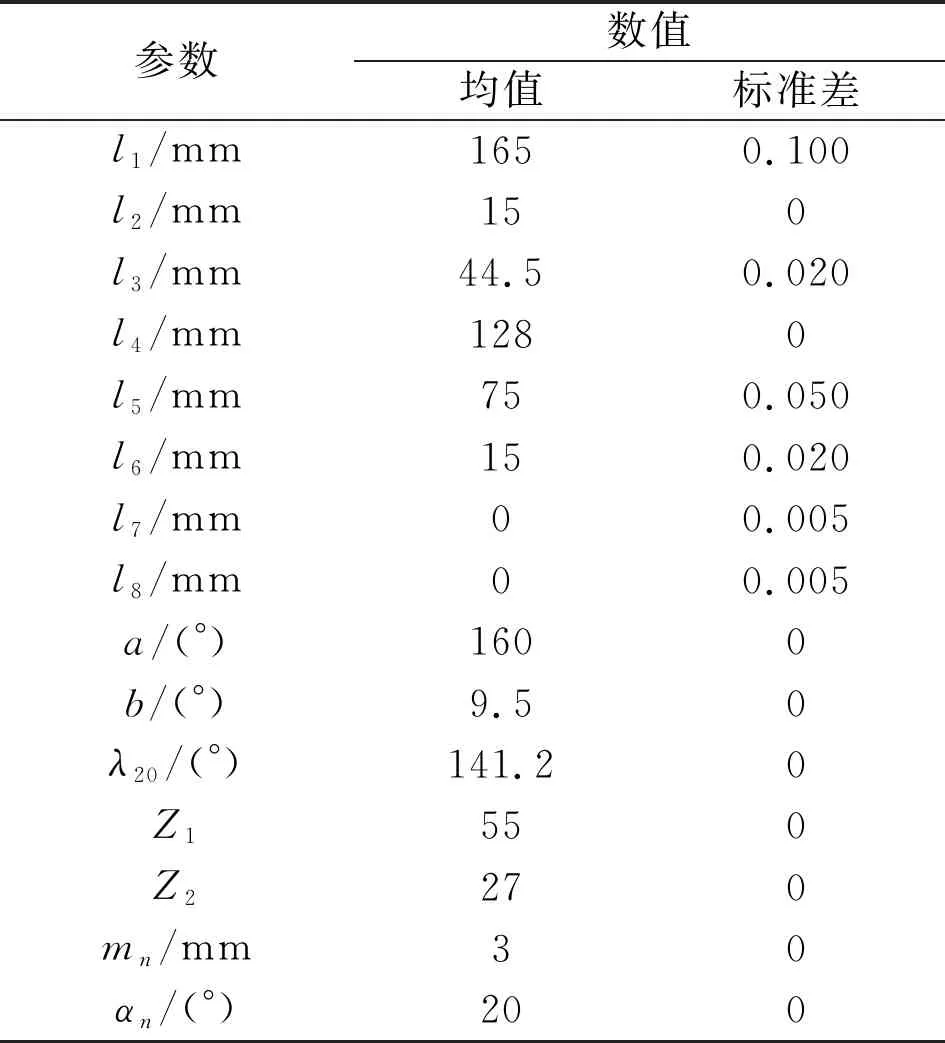
表1 快速機構基本參數

采用蒙特卡羅(MCS)算法進行驗證,設定樣本容量為105,時間區間內離散點的個數為200。同時結合文獻 [3]中的首次穿越方法,計算各安全邊界下的失效概率,如表2所示。其中,e為安全邊界,pF、pF,MVFP和pF,MCS分別為本文方法、文獻 [3]方法和蒙特卡羅方法所得到的時變運動失效概率。定義相對誤差δ為

(45)

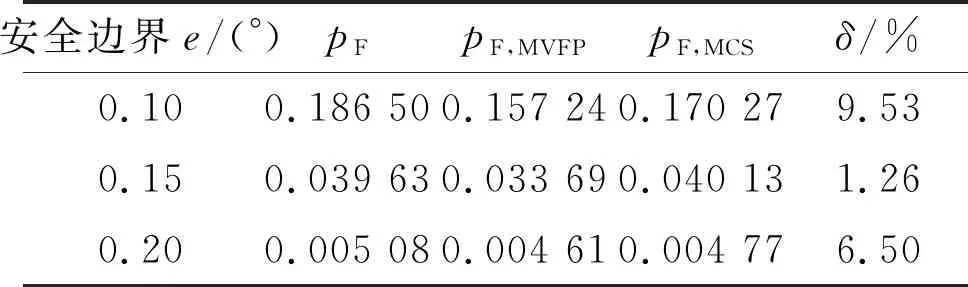
表2 3種方法得到的時變運動失效概率

針對安全邊界為0.15°時的快速機構,分別采用本文方法和MCS方法計算時變運動失效概率,得到的結果如圖11所示。由圖可見,2種方法計算出的失效概率均隨著輸入角度θ的增大而增大。

圖11 時變運動失效概率序列曲線Fig.11 Time-dependent kinematic failure probability sequence curves

在計算時間成本方面,本文方法針對每一個安全邊界,Matlab2021b軟件所需調用的函數次數為1,求解時變運動失效概率總調用函數次數為200×1=200。而蒙特卡羅方法總調用函數次數為200×105=2.0×107。2種方法所耗CPU(i7-6820HQ)時間的對比如表3所示,很明顯,本文方法的時間成本遠小于蒙特卡羅法,在計算效率上有著較大優勢。由此可見,本文所提出的方法具有較高的求解精度與計算效率,這為機構時變運動可靠性的快速準確計算和靈敏度分析提供了理論支撐。

表3 2種方法計算時間對比

綜上所述,在同一尺寸偏差下,隨著安全邊界范圍的增大,時變運動失效概率遞減。對于不同的安全邊界條件,采用本文方法計算出的時變運動失效概率與蒙特卡羅法的迭代運算結果十分接近,相對誤差小于10%,能夠滿足工程實際要求。

更改表1中部分機構尺寸參數,如表4所示,計算在此參數下快速機構的時變運動失效概率,結果列于表5。可以看到,此時的相對誤差值同樣符合工程需求,再一次驗證了本文方法的有效性。

表4 快速機構基本參數

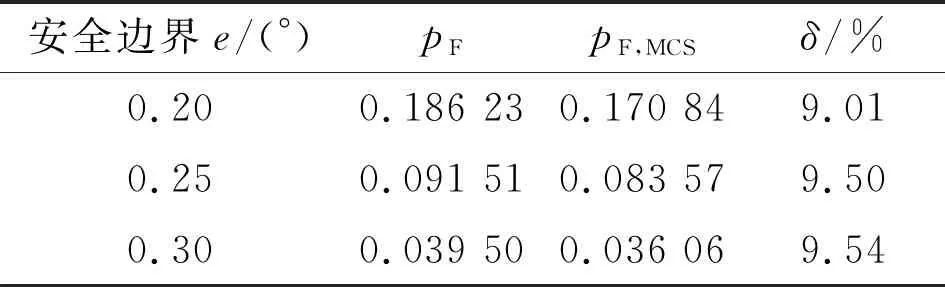
表5 2種方法得到的時變運動失效概率

根據以上結果,適用于整個時間區間上的時變可靠性模型已成功建立,這為時變可靠性問題中靈敏度的求解提供了前提。下面根據表1中機構的基本參數進行靈敏度分析。

由誤差函數得到X=(l1,l3,l5,l6,l7,l8)為服從正態分布的六維隨機變量,X的均值與標準差分別為μX=(μ1,μ3,μ5,μ6,μ7,μ8)和σX=(σ1,σ3,σ5,σ6,σ7,σ8)。根據式(15),可得到由于單位均值和標準差變化所引起的失效概率響應,即均值靈敏度和標準差靈敏度,分別表示為

(46)

(47)

給定安全邊界e=0.15°,根據式(46)和(47),可計算出采用本文方法得到的靈敏度參數,如表6所示。

表6 快速機構可靠性靈敏度分析

由表6可知,均值靈敏度指標按絕對值由大到小排序為Sμ5、Sμ6、Sμ3、Sμ1、Sμ8、Sμ7,均值μ5對時變運動失效概率的影響最大,即μ5的微小波動便可對儲能過程的可靠性產生較大影響,μ7和μ8的影響程度接近。均值靈敏度Sμ5、Sμ6和Sμ8為負值,表示時變運動失效概率隨著均值的增大而減小;若靈敏度為正值,則變化趨勢正好相反。標準差σ3對時變運動失效概率的影響最大,σ7的影響最小,且標準差靈敏度指標由大到小的排序為Sσ3、Sσ6、Sσ5、Sσ1、Sσ8、Sσ7。

根據以上分析,在所有的隨機變量分布參數中,參數μ5和σ3對于時變運動失效概率有著重要影響。因此,在設計制造與加工裝配過程中,應重點關注撥釘與齒輪1的裝配精度以及偏心凸輪的偏心圓幾何半徑尺寸公差。

5 結 論

(1)分析了有載分接開關快速機構運動失效的影響因素,重點考慮了零部件在加工與裝配過程中的隨機誤差,從而建立了時變運動可靠性分析模型,提出了一種以首次穿越法求解時變運動可靠性理論為基礎,在均值處基于多維高斯分布隨機過程的時變運動失效概率求解方法。該方法結合首次穿越方法中穿越上邊界和下邊界的穿越率概念,運用單變量正態函數的一階原點矩,評估了機構隨時間變化的運動可靠性。

(2)針對有載分接開關快速機構儲能過程,快速準確地計算出了某一安全邊界下的時變運動失效概率,實現了概率壽命預測。推導了快速機構時變運動可靠性靈敏度解析公式,計算結果表明:l7與l8的微小波動對于儲能過程的可靠性影響較小,在機構設計優化時可忽略,而是需要重點考慮裝配過程中安裝在齒輪1上的撥釘的定位誤差,以及偏心凸輪的偏心圓幾何半徑尺寸公差。

(3)在實際工程應用中,當構件尺寸公差較小時,本文方法精度高且計算成本低,可替代蒙特卡羅方法的多重迭代機制,用來指導關鍵部件的加工裝配,以滿足機械動作的可靠性與穩定性,避免因服役過程中的運動誤差超出安全邊界而造成的失效。