拉桿轉子接觸界面參數識別和動力學研究進展

李浦,袁奇

(西安交通大學葉輪機械研究所,710049,西安)

拉桿組合式轉子具有剛度大、重量輕和便于布置冷卻通道等優點,被廣泛應用于燃氣輪機和航空發動機。與整體轉子不同,拉桿轉子接觸界面多,接觸狀態復雜,工作在高溫、高壓、高轉速環境。據統計,燃氣輪機轉子系統的故障率占比高達45%,運維費用占整個電廠的60%以上[1]。因此,結構可靠性和完整性對機組安全、穩定運行具有決定性作用。拉桿轉子的設計主要考慮以下因素:壓氣機和透平部分的通流形狀、葉片安裝及葉片承受的載荷、冷卻和密封氣體流道的布置、額定載荷和故障狀態下傳扭的可靠性和結構完整性等。

深入開展螺栓連接拉桿轉子的動力學機理研究,是重大裝配體可靠性的重要支撐,但對于螺栓連接拉桿轉子的固有頻率和動力學特性研究,目前并沒有給出統一的設計準則。由于多組合界面非線性行為受激振力和運行狀態的影響,需要考慮幾何結構、界面參數不確定性和多支撐邊界條件等因素,因而導致傳統的正向分析無法準確預測結構的模態特性和動力學響應。有限元模型修正理論廣泛應用于工程技術領域,線性模型修正理論經過多年發展已日趨成熟,但作為線性理論的重要推廣,非線性參數識別和模型修正目前尚處于起步階段。近年來,非線性參數識別技術已成為燃氣輪機和航空發動機建模的重要方法之一,例如普惠公司在MIT燃氣輪機實驗室建立雙轉子渦扇整機實驗平臺[2],開展了轉子模態參數和氣動阻尼識別研究。

針對接觸界面建模、模態試驗和參數識別,學者們開展了大量的研究工作。從轉子設計角度出發,如要保證轉子的結構完整性,預緊力是一個關鍵參數。本文主要討論了拉桿轉子接觸界面參數識別和轉子動力學特性方面的研究進展,首先總結了燃氣輪機拉桿轉子結構完整性方面的研究結果,包括轉子結構、端面齒連接和完整性分析等;其次歸納了接觸界面剛度分析模型;然后,介紹了非線性參數識別方法并總結了拉桿轉子接觸參數識別的相關研究;最后,討論了拉桿轉子動力學的研究成果和拉桿預緊力設計方法,并展望了未來的研究方向。

1 拉桿轉子結構完整性

重型燃氣輪機常用于發電領域,可認為是大功率工業燃氣輪機。另一種常用的燃氣輪機由航空發動機改型而來,稱為航改燃氣輪機,常用于艦船和機車驅動。與重型燃氣輪機相比,航改燃氣輪機的效率相對較高,結構緊湊且功率密度大。

1.1 拉桿轉子結構特點

根據拉桿的布置結構,重型燃氣輪機轉子可分為周向拉桿和中心拉桿轉子,如圖1所示。周向拉桿轉子采用周向均布的多拉桿預緊連接,如美國通用公司、日本三菱重工等企業的燃氣輪機均采用此結構。中心拉桿轉子采用一根拉桿將整個轉子輪盤預緊,如德國西門子公司的燃氣輪機采用此結構。2種轉子結構的對比如表1所示,中心拉桿轉子采用端面齒輪盤傳遞扭矩,拉桿預緊力大,位置在輪盤中心,溫度相對較低,且沿軸向布置有阻尼元件,可調節拉桿振動頻率以避免共振;周向拉桿轉子采用帶凸臺的多拉桿結構,拉桿溫度相對較高,輪盤采用平面摩擦或端面齒盤傳遞扭矩。

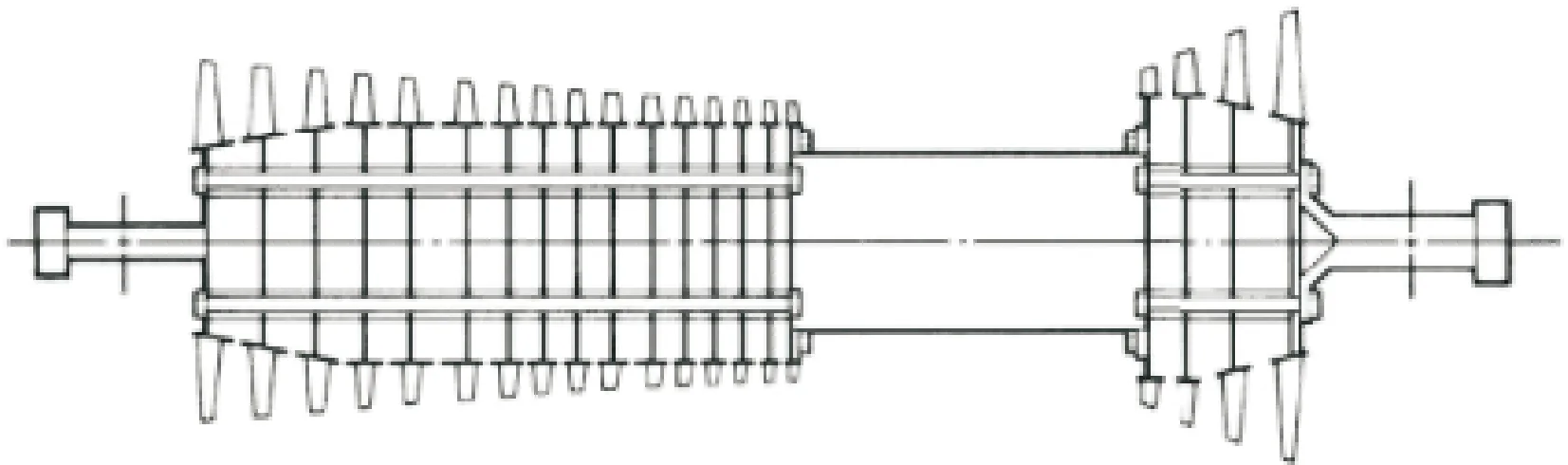
(a)周向拉桿轉子

(b)中心拉桿轉子

表1 中心拉桿和周向拉桿轉子結構對比

1.2 端面齒連接結構

根據傳扭方式,拉桿轉子的連接結構可分為平面摩擦傳扭和端面齒傳扭。端面齒盤具有自定心和傳扭大等優點,因此在重型燃氣輪機和航空發動機中得到廣泛應用,例如三菱公司M701F重型燃氣輪機的透平輪盤采用弧形齒(Curvic coupling)傳扭,西門子公司V94.3A重型燃氣輪機的壓氣機和透平輪盤均采用平面齒(Hirth coupling)傳扭。通用、西門子和三菱重工等廠商的F和H級重型燃氣輪機拉桿轉子盤軸的連接方式如表2所示。端面齒盤連接的可靠性更高,但齒形結構不可避免地會引入應力集中,齒面微動滑移非線性更加復雜,且對齒面加工精度的要求更高。

表2 重型燃氣輪機拉桿轉子典型連接方式

端面齒結構緊湊且剛性大,被廣泛應用于傳動裝置。由于全齒嚙合精度高,也可作為分度裝置。根據齒面形狀可將端面齒分為平面齒和弧形齒,其加工示意見圖2,特點對比匯總于表3。平面齒最早由Albert Hirth于1928年提出[3],主要用于機械傳動,通過側銑刀加工齒面,加工刀路銑削角γ導致齒形向心收縮。弧形齒為格里森(Gleason)公司發明,由一對曲率相同的凹齒和凸齒嚙合組成,采用成形砂輪或齒盤在專用磨齒機床上加工,得到要求的齒形齒面,弧形齒主要用于航空發動機以及燃氣輪機(如三菱公司)盤軸連接。

(a)弧形齒

(b)平面齒

表3 平面齒和弧形齒特點對比

1.3 結構完整性分析

燃氣輪機結構完整性主要是指在熱結構載荷和氧化腐蝕環境下,燃氣輪機強度、變形、振動和疲勞等特性能夠滿足設計要求[4]。拉桿轉子動力學是結構完整性的重要研究內容之一,多接觸界面誘發的非線性特征往往會導致振動異常甚至結構失效,因此結構完整性是保證其功能性的重要前提。從部件角度而言,需要對壓氣機葉片、透平葉片、轉子和氣缸等部件分別開展完整性分析。

拉桿轉子界面接觸剛度隨著預緊力的增加而增加,當預緊力達到一定程度時,拉桿轉子模態特性和整體轉子保持一致,此時稱為預緊飽和狀態,可采用轉子動力學的常規線性方法進行等效分析。隨著高溫、高轉速、大扭矩燃氣輪機的發展,拉桿預緊力在復雜載荷下無法保證接觸界面的連續性,不同轉速下轉子可能出現幅值突跳的“雙穩態”現象。拉桿在熱疲勞和熱腐蝕的耦合作用下產生應力松弛和裂紋,可能會導致整機振動甚至結構失效,例如某工業燃氣輪機的中空連接扭矩套筒螺栓在高溫和拉扭耦合載荷下曾發生了疲勞斷裂[5]。

圖3展示了拉桿轉子結構完整性分析的具體內容,并梳理了本文的思路。結構完整性分析主要包括結構強度分析和動力學分析兩方面,結構強度分析包括靜強度分析、蠕變分析和疲勞壽命分析等,動力學建模是動力學分析的基礎,包括軸承基礎建模和轉子部分建模。本文在第2章討論了基于接觸剛度的跨尺度接觸界面模型對拉桿轉子動力學特性的影響;在第3章總結了不確定非線性邊界條件下,基于模態試驗的用于確定螺栓連接結構和動力學響應的參數識別方法;第4章主要分析了線性和非線性轉子動力學模型和相關研究成果;在第5章討論了拉桿轉子的預緊力設計。

圖3 拉桿轉子結構完整性分析框圖Fig.3 Mechanical integrity analysis of tie-bolt rotors

2 接觸界面特性研究

2.1 接觸剛度模型

由于機加工表面在微觀上具有粗糙形貌,導致兩輪盤的實際接觸面積小于名義接觸面積,因此拉桿轉子的剛度可認為是由轉子基體剛度和接觸層剛度兩部分串聯而成。不同于連續基體結構,接觸剛度呈現出頻響函數隨預緊力和激振力變化的非線性特征。因此,接觸剛度分析是拉桿轉子精確建模和動力學響應計算的基礎,一般可分為正問題和反問題。正問題即基于微觀接觸模型建立接觸剛度和預緊力、微觀形貌參數以及材料參數的關系,反問題即通過模態試驗識別接觸界面參數。

針對粗糙表面微凸體接觸,理論分析模型主要可分為統計學模型和分形模型[6]。赫茲(Hertz)接觸給出了剛性球體與彈性平面之間接觸壓力、滲透量和接觸半徑的表達式,是接觸力學模型的基礎[7]。Archard指出平面彈性接觸面積和壓力近似成正比關系[8]。Greenwood和Williamson等基于統計學理論,指出粗糙面微凸體服從高斯函數假設,并建立了兩平面彈性接觸(GW)模型,將Hertz接觸模型擴展到平面接觸[9]。Pullen和Williamson研究了粗糙面塑性接觸的表面力學行為[10]。Chang等基于微凸體體積守恒理論,構建了粗糙表面的彈塑性接觸(CEB)模型,并通過塑性指數對彈塑性變形進行定量化分析[11],從而建立了聯系微凸體彈性和塑性接觸的橋梁。Zhao等采用對數函數和多項式函數發展了微凸體的微接觸模型[12-13]。

分形模型假設粗糙接觸面具有自仿射分形特征,利用分形粗糙度和分形維數描述接觸特性。Mandelbrot等提出了用分形參數表征金屬表面的分形特征[14]。針對粗糙面接觸的多尺度效應,Majumdar和Bhushan指出微凸體尺寸服從冪律分布[15],并建立了彈塑性接觸分形(MB)模型,揭示了接觸壓力、接觸面積和分型參數之間的關系[16]。Yan和Komvopoulos基于兩變量Weierstrass-Mandelbrot函數,建立了粗糙接觸面的三維形貌模型,并用于彈塑性力學分析[17]。張學良等建立了具有尺度獨立性的接觸剛度和切向剛度分形模型[18-19]。Pohrt和Popov采用邊界元法分析了法向接觸剛度和分形參數的關系[20]。Zhang等基于接觸界面參數識別方法,建立了接觸剛度和分形參數的理論模型,并和Pohrt-Popov接觸剛度模型進行了對比分析[21]。

綜上所述,統計學模型基于微凸體高度概率密度函數,能夠描述剛度和阻尼能量耗散特性,但微觀形貌特征與采樣長度和儀器分辨率有關;分形模型根據分形參數建立了微凸體接觸面積分布密度函數,也能夠得到界面剛度和阻尼能量耗散特性,但并非所有的接觸表面都具有分形特征。

2.2 拉桿轉子接觸界面建模

開展拉桿轉子模態和動力學特性分析,需要先構建微觀接觸剛度與宏觀彎曲剛度和扭轉剛度之間的關系,即考慮接觸界面的拉桿轉子模型。饒柱石和夏松波等采用剛度修正的傳遞矩陣法,對拉桿轉子進行了模態分析[22]。Kim等針對發電機組合轉子,研究了預緊力對剛度的影響,提出了預緊飽和概念[23]。王艾倫等采用鍵合圖法對拉桿轉子的剛度進行了理論分析[24-25]。

近年來,有限元模型被廣泛應用于轉子動力特性分析,主要包括一維梁單元、二維軸對稱單元和三維實體單元等,其中一維梁單元需要對轉子進行簡化,二維軸對稱單元和三維實體單元可實現CAD和有限元分析的直接轉換。針對接觸界面的模型單元主要有3種:節點接觸單元、零厚度單元和薄層接觸單元[26]。節點接觸單元在接觸節點之間建立了一個等效的彈簧阻尼單元,以表征接觸剛度的影響,適合模擬一維梁單元接觸效應。對于面單元接觸,需要界面節點一一對應,如果考慮所有節點的非線性剛度,瞬態計算將非常耗時。何鵬等基于GW模型,得到了采用集總鉸鏈表征的等效剛度,并建立了拉桿轉子的一維有限元模型[27]。Gao等基于GW模型建立了考慮彎矩和輪盤分離故障下的彎曲剛度[28],通過扭轉彈簧考慮輪盤接觸剛度,并基于一維耦合有限元單元開展了轉子模態試驗和數值分析,試驗實物圖如圖4所示。

圖4 拉桿轉子模態試驗實物圖[28]Fig.4 Modal experiment of a bolt-fastened rotor[28]

零厚度單元是一種等參數接觸單元,通過形函數和節點位移定義接觸法向剛度和切向剛度矩陣,最早用于地質力學中的巖石耦合模型[29]。Oh等基于GW模型構建了接觸剛度和應力分布之間的關系,提出了一種考慮接觸剛度的預應力模態分析方法[30]。Balaji等采用零厚度單元法建立了螺栓連接的多尺度非線性模型,將其用于螺栓搭接結構的非線性模態分析[31]。薄層接觸單元(也稱虛擬材料法)是在接觸面之間構建一個薄實體單元,通過接觸層的線性本構關系考慮接觸剛度對系統的影響。Yao等針對航空發動機螺栓連接結構,提出了一種改進的薄層接觸單元,通過分區域修正接觸剛度提高了模型精度[32]。Ma等基于薄層單元建立了螺栓法蘭連接轉子的有限元模型,并采用區間法開展了轉子不確定性分析[33]。Du等基于分形接觸模型和虛擬材料法開展了拉桿轉子模態分析和動力學分析[34]。Rimpel等提出了一種虛擬薄層的彈性模量修正方法,通過拉桿轉子模態分析進行驗證,并用于某離心壓縮機的中心拉桿轉子試驗,如圖5所示[35]。研究表明,接觸面止口配合會引起接觸狀態改變,導致測量模態頻率發生階躍變化。趙潤超等根據轉子接觸特性給出了虛擬材料參數的建模方法,并將其用于動力學特性計算,結果表明預緊力變化對第四階臨界轉速的影響達2.31%[36]。

圖5 離心壓縮機拉桿轉子模態試驗實物圖[35] Fig.5 Modal experiment of a tie-bolt rotor of a centrifugal compressor[35]

相比于平面摩擦接觸,端面齒盤廣泛用于燃氣輪機和航空發動機,是更加可靠的拉桿轉子定位和傳扭結構。尹澤勇等針對端齒連接轉子,采用端齒梁單元開展了轉子動力特性分析和軸向預緊力設計研究[37-38]。Yuan等分析了弧形端面齒連接的重型燃氣輪機的界面等效剛度,基于彎曲中性層理論推導了節點接觸剛度,結果表明端面齒的界面波紋度對轉子等效剛度和動力學特性具有顯著影響,而對粗糙度的影響較小[39]。Liu等針對弧形端面齒盤結構建立了三彈簧等效剛度模型,并采用三維有限元進行驗證,結果表明壓力角對端面齒盤接觸剛度弱化效應的影響顯著[40]。Liu等采用節點單元法模擬了端面齒對的黏滯滑移效應,并對預緊力松弛下的端面齒盤轉子進行了數值分析[41]。Yu等考慮了微凸體高度分布標準差、平均半徑和接觸角等影響因素,基于GW模型分析了端面齒盤接觸彎曲剛度,研究表明端面齒盤連接的彎曲剛度要小于平面接觸的彎曲剛度[42]。Kim等基于GW模型,構建了三維有限元多尺度迭代接觸模型和模態分析流程,開展了端面齒盤模態試驗,提出了連接剛度和應力協同分析方法[43-44]。圖6展示了Hirth齒盤連接的轉子模態試驗實物圖。

圖6 Hirth齒盤連接結構模態試驗實物圖[43]Fig.6 Modal experiment of a tie-bolt rotor with Hirth couplings[43]

綜上所述,采用節點單元法和零厚度單元法可以直接模擬接觸界面的非線性特性,但建模相對復雜;薄層單元法采用等效線性模型表征界面非線性特征,有限元建模相對簡單,但無法從物理機理層面描述其接觸行為。端面齒盤模型一般采用等效梁單元或三維實體單元,多齒面微觀彈塑性接觸模型的研究還很不充分,多尺度接觸剛度和動力學響應的耦合機理更是有待深入研究。

3 拉桿轉子接觸界面參數識別

3.1 非線性參數識別方法

在“雙碳”目標的大背景下,復合材料在燃氣輪機和航空發動機轉子、機匣等部件應用廣泛。由于螺栓連接的拉桿轉子結構日趨輕量化和復雜化,非線性在結構動力學的分析中不可忽略。由于材料參數和接觸參數的不確定性,一般需要采用非線性識別方法來進行模型修正和確定。非線性系統辨識包括非線性檢測、非線性特征描述和參數估計等[45]。Kerschen等將非線性系統辨識方法分為回復力面法(或力狀態映射法)、直接參數估計法、非線性自回歸滑動平均(NARMAX)模型法、Hilbert變換法、Volterra級數法、模態參數法等[45]。Kerschen等在2017年進一步將識別方法歸總為線性化法、時域法、頻域法、時頻域法、模態方法、黑盒法以及模型修正方法[46]。

非線性參數識別可以分為全局非線性和局部非線性兩大類。全局非線性是指大部分結構發生非線性行為,如大載荷引起的結構幾何非線性等。局部非線性只是在局部有限范圍內發生的非線性行為,其他部分仍然是線性的,大多數螺栓預緊的組合結構都存在局部非線性。對于多自由度動力學系統,Zhang等提出了基于頻響函數重構試驗的非線性參數識別法,得到了對應線性系統的等效剛度和等效阻尼[47]。考慮非線性力的多自由度動力學方程可表示為

(1)

基于等效剛度和等效阻尼的非線性系統可以表示為

(2)

式中:Keq、Deq分別為參數識別法得到的等效剛度矩陣和等效阻尼系數矩陣。

拉桿轉子是一種特殊的螺栓連接結構,國內外開展了大量關于螺栓搭接和螺栓法蘭連接的研究工作,螺栓連接跨尺度模型為拉桿轉子建模提供了一種研究方法。但是,拉桿轉子的靜態模態分析不能預測轉動下復雜非線性特征,且多種組合接觸狀態(法向接觸、切向止口接觸和齒盤接觸等)不確定性誘發的轉子振動異常現象的機理尚不清楚。

3.2 拉桿轉子接觸參數識別

相比螺栓搭接結構和螺栓法蘭連接,拉桿轉子一般具有多對接觸面,可能會承受預緊力、不平衡力和扭矩等組合載荷。如圖7所示,Zhang等采用均布彈簧模擬接觸界面,根據不同粗糙度和預緊力下的模態敲擊試驗結果,識別和修正了有限元模型的界面彈簧剛度,給出了接觸剛度隨名義壓力的變化曲線,并應用于某實際燃氣輪機轉子的模態分析[48]。結果表明:透平和壓氣機輪盤接觸剛度在1013N/m3量級,真實燃氣輪機拉桿轉子融合接觸剛度的有限元分析和模態試驗結果最大誤差為1.14%,證明了所用模型的正確性。

圖7 拉桿轉子自由敲擊模態試驗[48]Fig.7 Modal experimental of a rod-fastened rotor under free-free boundary condition using a hammer excitation method[48]

張子陽等提出彈簧剛度矩陣和有限元模型剛度矩陣融合修正方法,分析了航空發動機拉桿轉子的接觸狀態[49]。高進等基于彈簧連接的梁單元建立了拉桿轉子模型,采用彈簧線性剛度表征了梁單元的階梯軸結構突變和接觸效應雙重剛度弱化,并基于靈敏度分析開展了轉子模型修正,如圖8所示[50]。

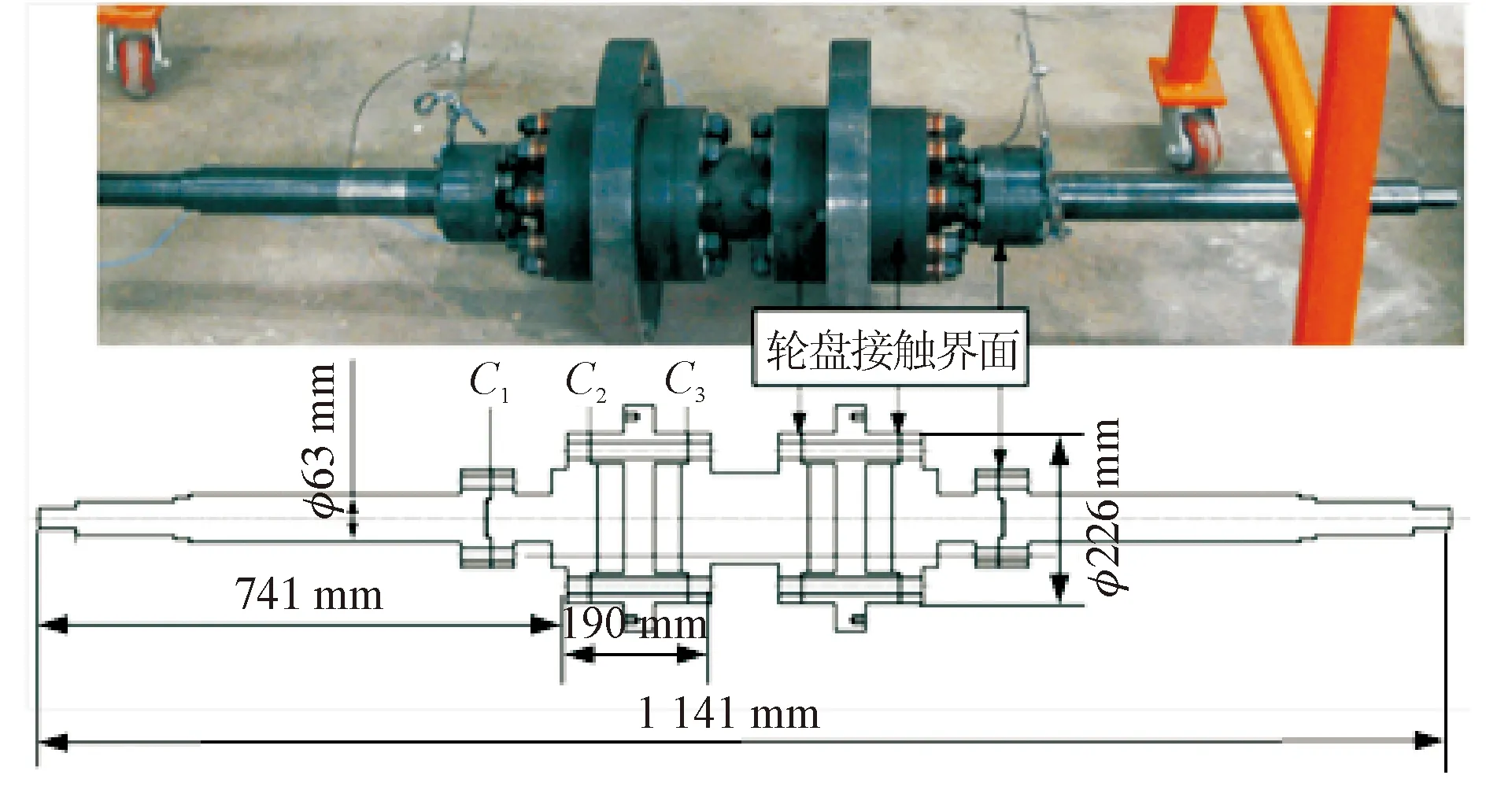
圖8 拉桿轉子模型修正試驗[50]Fig.8 Model updating of a rod-fastened rotor[50]

繆輝等采用薄層單元開展空氣循環機拉桿轉子界面動力學研究,提出了部件模型修正和連接模型修正的分層模型修正方法[51],基于靈敏度分析選擇待修正參數,通過修正分層模型對接觸界面連接剛度進行了準確識別,并與試驗結果作對比驗證了方法的正確性。圖9展示了空氣循環機拉桿轉子模態試驗實物圖。

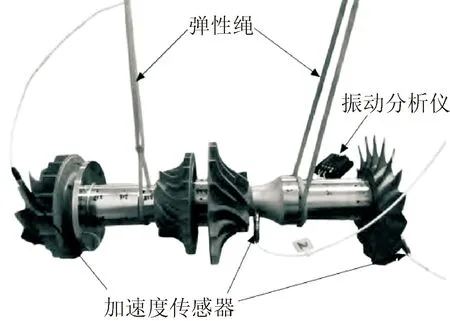
圖9 空氣循環機拉桿轉子模態試驗[51]Fig.9 Modal experiment of a rod-fastened rotor of an air cycle machine [51]

Li等采用虛擬材料法開展了拉桿轉子模態試驗分析和接觸剛度阻尼參數識別,結果表明:過盈止口連接導致接觸剛度隨著預緊力的增加呈現雙線性特征,由于接觸面狀態發生改變,接觸阻尼在雙線性轉折點出現了突跳現象[52]。趙廣等采用雙薄層單元法建立了盤鼓螺栓連接結構的接觸剛度模型,并基于模態試驗開展了剛度識別研究[53]。Zou等針對高壓發動機盤鼓式轉子開展了預緊力和接觸狀態參數識別研究,試驗如圖10所示,采用力矩扳手控制24個周向均布螺栓預緊力,分別在20%和40%預緊不均狀態下,通過敲擊試驗識別各階模態頻率,結果表明響應頻率對于局部螺栓松動的識別靈敏度較低,由此提出了低階模態相移法和高階模態響應偏差法的綜合識別方法[54]。邊濤等采用Hilbert-Huang變換方法對拉桿轉子模態參數進行了識別[55]。顏正杰等基于BP神經網絡,采用粒子群法對拉桿轉子結合面的特性參數進行了優化識別[56]。

圖10 高壓發動機拉桿轉子模態試驗[54]Fig.10 Modal experiment of a rod-fastened rotor of high pressure engine[54]

綜上所述,針對螺栓連接界面的不確定性,眾多學者開展了界面參數識別研究。目前,大多數參數識別研究聚焦于平面連接的螺栓連接結構,針對端面齒盤連接的參數識別研究較少。此外,參數識別大多數基于自由模態敲擊試驗,通過改變預緊力實現改變接觸剛度轉子的模態分析。但實際上,非線性轉子動力學特性與激振力密切相關,在不同激振力作用下了解轉子的響應峰值頻移現象和遲滯特性具有十分重要的意義。從數學模型角度而言,由于特征值和特征向量與轉子頻率和振型相對應,因此分析拉桿轉子振動頻率的變化趨勢需要結合振型特征進行綜合評判。

4 拉桿轉子動力學分析

螺栓連接的轉子-軸承系統動力學建模和振動特性分析,主要包括線性動力學和非線性動力學兩個方面,從數值方法角度可分為時域計算和頻域計算。線性動力學分析采用線性彈簧耦合接觸面節點,或線性薄層單元修正接觸剛度,對臨界轉速和不平衡響應進行分析。高銳等考慮接觸面剛度對轉子動力學的影響,采用線性鉸鏈單元和一維梁單元對某型重型燃氣輪機開展了臨界轉速分析[57]。Jam等采用一維梁單元建立了某商業燃氣輪機中心拉桿轉子模型,通過考慮預應力剛度矩陣對預緊力的影響,計算出的固有頻率最大誤差達10%,說明僅考慮預應力載荷無法準確模擬界面接觸對動力學的影響[58]。Wagner等針對某拉桿轉子,采用兩步法進行拉桿轉子臨界轉速計算,根據靜態應力分析確定接觸面狀態,并通過多點耦合方法(MPC)建立了考慮接觸狀態的動力學分析模型。與整個界面耦合模型相比,此方法考慮了局部應力不均勻導致的剛度弱化效應,可認為是一種應力-動力單向耦合模式[59]。Xu等在不同預緊力作用下,采用節點單元法推導了拉桿轉子的運動方程,計算了轉子的彎曲固有頻率[60]。

拉桿轉子非線性動力學包括界面非線性、軸承參數非線性以及故障(碰摩、不對中等)引起的非線性。錢征文等針對盤式拉桿轉子出現的“雙穩態”振動問題,將接觸剛度等效為非線性剛度的抗彎彈簧,采用諧波平衡法和同倫算法分析了轉子的振動特性[61]。Hei等采用三次方剛度非線性彈簧表征接觸剛度,建立了拉桿轉子-滑動軸承系統的動力學模型,并基于Newmark方法開展了非線性動力學分析[62]。Hu等考慮油膜力、不平衡載荷以及拉桿預緊力等因素影響,建立了周向拉桿轉子的運動微分方程,并采用Runge-Kutta法進行數值求解,分析了轉子在不同參數下的非線性響應[63]。Li等針對多盤拉桿轉子定點碰摩,采用直接數值積分法開展了非線性振動分析,研究了不同碰摩位置下的轉子動態響應[64]。Liu等采用三維有限元縮減模型,分析了界面加工誤差對拉桿轉子動態響應和穩定性的影響規律[65]。Wang等基于三維有限元模型分析了裂紋對拉桿轉子動力學特性的影響[66]。金淼等針對端面齒預緊的拉桿轉子,基于梁單元模型建立了中心拉桿-轉子-葉片耦合系統動力學分析模型,并進行了臨界轉速和不平衡響應分析[67]。Wang等分析了拉桿轉子輪盤之間的內阻尼對轉子動力學響應和穩定性的影響,指出內阻尼會減小失穩閾值轉速[68]。Liu等針對拉桿裂紋故障,引入裂紋修正系數來描述拉桿松動,通過建立時變剛度矩陣,研究了周向拉桿裂紋對轉子非線性動力學性能的影響[69]。Zhang等基于集總參數法和立方非線性剛度建立了雙盤拉桿轉子軸承系統的動力學方程,并采用數值積分法分析了多參數對非線性特性的影響[70-71]。Hong等考慮螺栓松動引起的殘余預緊力,提出了一種新的非對稱螺栓預緊力的呼吸模型,通過建立轉子參數機理分析模型,研究了不對稱殘余預緊對航空發動機組合共振的影響,并采用某實際雙轉子進行了試驗驗證[72]。王奇等針對拉桿預緊不均引起的振動局部化現象開展了理論研究,提出當激振頻率位于一定頻段內時,振動能量在局部集中從而誘發了振動局部化現象[73]。羅忠等總結了組合支承轉子系統模型建模法、高維降維法、非線性動力學微分方程求解法、組合支承非線性問題等對轉子系統振動特性的影響機理,指出了組合支承轉子系統研究中值得關注的問題[74]。

綜上所述,近年來針對拉桿轉子的動力學分析主要集中于故障引起的非線性特性,如碰摩、拉桿松動和突加載荷等,具體分析方法可分為時域和頻域兩種,如直接數值積分法和諧波平衡法。相比于一般的線性轉子動力學分析,由于非線性分析計算耗時嚴重,一般采用一維梁單元或三維縮減模型對拉桿轉子進行簡化;對于拉桿松動、動壓油膜潤滑軸承等引起的非線性力,一般采用等效模型進行處理。

5 拉桿轉子預緊力設計

復雜邊界條件下,拉桿轉子的動力學響應一般都是非線性的。對于大多數重型燃氣輪機轉子,只要拉桿預緊力足夠大,就能保證轉子在運行轉速范圍內始終處于接觸狀態,但預緊飽和并無統一的量化標準。對于航空發動機轉子,由于頻繁變工況運行,大量螺栓連接結構呈現復雜的非線性特征,因此拉桿預緊力是拉桿轉子十分重要的設計參數之一。

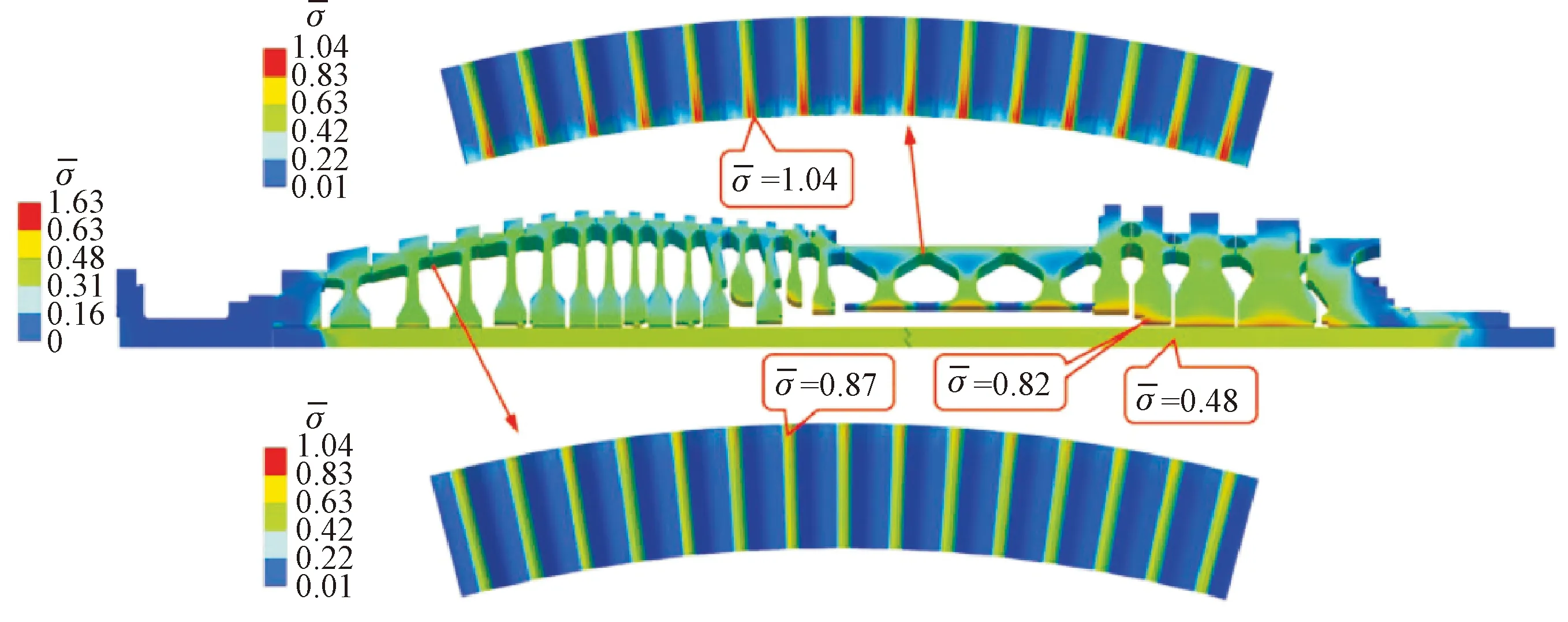
圖11 F級拉桿轉子穩態運行應力分布圖[76]Fig.11 Stress distribution of a F class gas turbine tie-bolt rotor under steady state conditions[76]

典型商業燃氣輪機輪盤預緊力名義壓力如表4所示[77]。可以看出,預緊力下的名義應力高達數十甚至上百兆帕,并沒有一個統一的標準。對于重型燃氣輪機,工程中一般將無量綱預緊力,即預緊力與輪盤自重所引起的彎曲產生的軸向脫開力比值,作為設計準則。為了保證輪盤不脫離,無量綱預緊力應大于1。考慮一定的安全裕度,實際工作中燃氣輪機的無量綱預緊力應保證在4～8之間。此外,預緊力設計還需要考慮轉子傳遞扭矩的能力。隨著預緊力增加,轉子能夠傳遞更大扭矩,但接觸應力增大會帶來強度問題[78]。對于航空發動機轉子,由于重量小且大多為鼓筒薄壁結構,多螺栓預緊的不確定性和大載荷的殘余預緊力更易誘發轉子產生非線性振動。

表4 典型F級重型燃氣輪機轉子接觸界面名義壓力

6 總結與展望

拉桿轉子作為燃氣輪機和航空發動機的重要旋轉設備,了解其界面接觸狀態和動力學響應的耦合機理,對整機動態性能的預測和可靠性分析具有重要意義。拉桿轉子結合界面主要包括平面接觸和端面齒盤連接兩種類型,還需考慮止口、拉桿孔等配合面的接觸狀態。從宏觀角度而言,拉桿轉子可認為是一種螺栓連接的裝配體。針對平面接觸的拉桿轉子,如何提升和保證裝配界面接觸壓力的均勻性,以及如何減小應力集中,是解決整機振動和零部件疲勞失效的關鍵所在。端面齒盤具有定位準確和傳扭可靠等優點,但同時也引入了新的挑戰和問題:①齒形結構決定了其固有的應力集中現象,無法保證界面應力均勻;②齒盤接觸剛度需要綜合考慮齒面微觀形貌特征和宏觀齒形參數;③齒面非對稱接觸下的黏滯-滑移現象更加復雜;④對彈性耦合的多齒對開展接觸分析,需要兼顧模型精度和計算耗時。

隨著高溫、高轉速、變工況發動機的發展和輕型復合材料的廣泛應用,螺栓連接多接觸界面的非線性接觸剛度和阻尼特性對結構動力學響應的影響越發明顯。基于模態試驗的參數識別是多組合體精確建模的重要方法之一。對于螺栓搭接和法蘭連接結構,國內外學者開展了深入的理論分析和試驗研究,但其本構模型和計算結論無法直接應用于燃氣輪機拉桿轉子的動力學分析。這是因為,拉桿轉子的邊界條件十分復雜,需要考慮諸如高溫、高轉速、變工況下等環境下的拉桿殘余預緊力和響應的動態耦合。另外,拉桿轉子的結構和連接狀態也非常復雜,如多級軸流式轉子法向平面接觸、切向止口定位和端面齒盤等多接觸面之間的耦合關系,并非簡單的螺栓板狀搭接結構能夠反映。綜上所述,可歸納出以下有待解決的問題。

(1)針對拉桿轉子微觀形貌到宏觀動力學跨尺度問題,有必要建立更為準確可靠的本構模型和參數映射關系,尤其是對于端面齒連接結構,需要綜合考慮宏觀齒形結構和微觀形貌特征,用以闡明多尺度協同作用機理。

(2)針對不同邊界條件下模型非線性界面參數的不確定性開展模型參數識別研究,建立不同激勵水平下的非線性響應變化關系。隨著深度學習技術的快速發展,數據驅動的動力學建模方法和參數識別,為拉桿轉子精確建模提供了新的思路和方法。

(3)開展多物理場耦合的拉桿轉子非線性動力學分析,需要兼顧計算效率和精度。考慮建立描述拉桿轉子動力學性能的降階模型和協同仿真數值計算方法,為復雜轉子動力學分析提供可能。

(4)考慮拉桿預緊失諧和裝配界面典型故障,建立不同結構參數和運行工況下的轉子飽和預緊力設計準則,為轉子界面的加工和裝配工藝提供理論指導。