虹吸管道比沖洗能力影響參數研究*

童 越 周宏志 李占福

(1 天津職業技術師范大學電子工程學院 天津 300222)

(2 福建理工大學機械與汽車工程學院 福州 350118)

在自然界中,虹吸是根據液體表面水平差產生的一種特別的力[1～2]。國內大部分的衛浴公司在設計虹吸管道的時候大部分都依靠仿制或傳統工藝,缺乏新技術優化虹吸管道,不斷加劇中國水資源的匱乏。劉少春應用計算流體動力學(CFD)對虹吸馬桶沖洗整個過程進行了仿真研究,但是沒有進行參數調節變化實驗[3～4]。張榮譽通過改變水箱的水量進行實驗研究,參數單一且沒有充足的數據量[5]。李庚等對虹吸式馬桶進行了負壓瞬時抽水的試驗,數據較準確,但結構不夠簡單[6]。虹吸管道的參數直接影響著坐便器沖洗的性能。

筆者希望通過實驗的探究來優化虹吸管道。以馬桶虹吸流道為基礎的試驗研究,筆者定義并提取了綜合的沖洗性能指標,并對4個對虹吸力產生影響的因素及與清洗效果的關系進行了分析,利用正交實驗得到4個參數的顯著性主次關系,同時得到優方案的參數組合,對虹吸管結構進行優化以改善其沖洗效果。

1 虹吸管道的參數與性能評價指標

1.1 虹吸管道的主要參數介紹

圖1是一種虹吸管道的構造。其結構由α、d1、H2、d2四個參數來表征,α表示虹吸管道一次水封的傾斜坡度,H1表示虹吸管道一次水封高度,d1為BC-E弧度變化的長,d2為E-F二次水封的高,H2度為E-F二次水封的寬。α、d1、L2、d2分別命名為傾斜坡度、曲率寬、二次水封寬、二次水封高。

圖1 虹吸管道的結構圖

1.2 虹吸管道的沖洗性能的評價指標

本實驗采用水沖小球來檢測馬桶的沖洗性能。在該研究中規定水的體積(V)為5.4 L,小球的體積是固定的,沖洗總個數為120個。

綜合沖洗性能的評價指標-比沖洗能力:指單位體積水量下虹吸管道的相對沖洗能力。其中相對沖洗能力指沖掉小球的體積與被沖小球的總體積的比值。

式中:H——比沖洗能力;n沖——被沖走的小球數目;

N總——總體的小球數目;V水——座便器水箱水量。

2 實驗裝置的介紹

為了研究傾斜角度、曲率寬度、曲率長度、二次水封寬度及二次水封高度等,把虹吸管道放入2個用機玻璃板制成的透明平板內,在水平和豎直方向上各鉆有一定間隔(10 mm)的小孔,利用在螺桿上加一個圓筒形襯套的方法進行補償調整,并在此基礎上組裝試水臺(水量檢測平臺),如圖2所示。

圖2 可調參數的坐便器實驗平臺

圖3 二次水封高與比沖洗能力的實驗結果

3 虹吸管道參數與比沖洗能力的關系

筆者希望通過單因素試驗法和正交試驗法來篩選出最優的一組實驗參數。

通過此組實驗的比較可發現,雖然對二次水封做的調整十分微小,但馬桶的沖洗性能改變非常多,由此可看出二次水封高度是一個重要的影響因素。在此試驗中,明顯發現:比沖洗能力與二次水封高度的關系近似線性函數,隨著二次水封高度的增加,比沖洗能力減少,但是當水封高度為0時,二次水封目的失效,所以選擇二次水封能力的高度10 mm 作為最佳參數。雖然降低二次水封的高度能有很大的效果,但當二次水封高度降到10 mm 以下時較難完成較為有用的二次水封。

3.1 二次水封寬對沖洗性能的影響

當二次水封過寬時,會導致沖洗小球所需能量較大。從圖4中可以看出,當水封寬大于80 mm 后沖走的小球減少。當二次水封寬小于80 mm 時,沖洗過程因為行程過短,致使小球在二次水封處發生堵塞,沖洗能量損失較大;當水封寬大于60 mm 時,堵塞較為嚴重,一次水封處也發成小球堆積現象,沖洗能力明顯降;當水封寬增大到70 mm 時,堵塞現象明顯減少,并 在水封寬為80 mm 時,比沖洗能力為最大值。

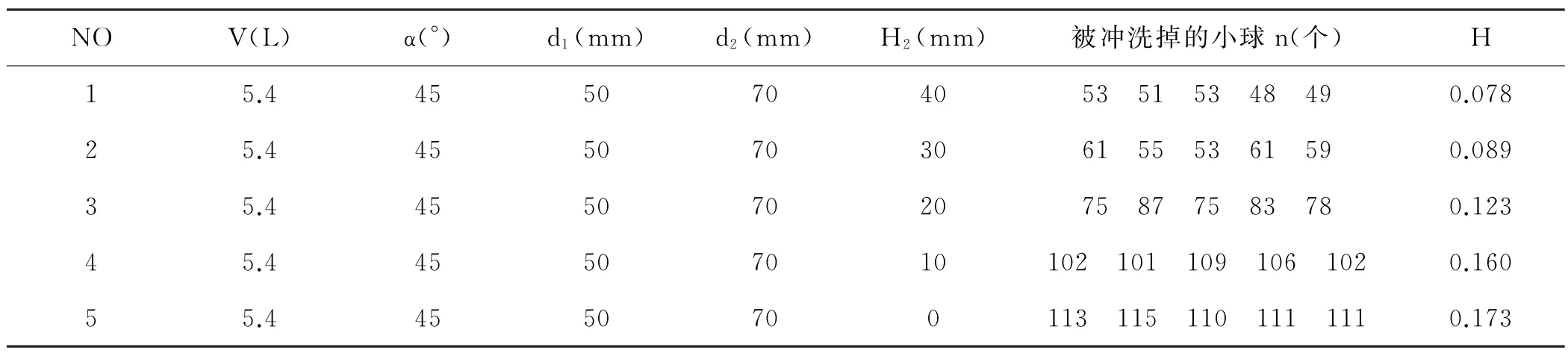
表1 二次水封高度的實驗設置

表2 二次水封寬度的實驗設置

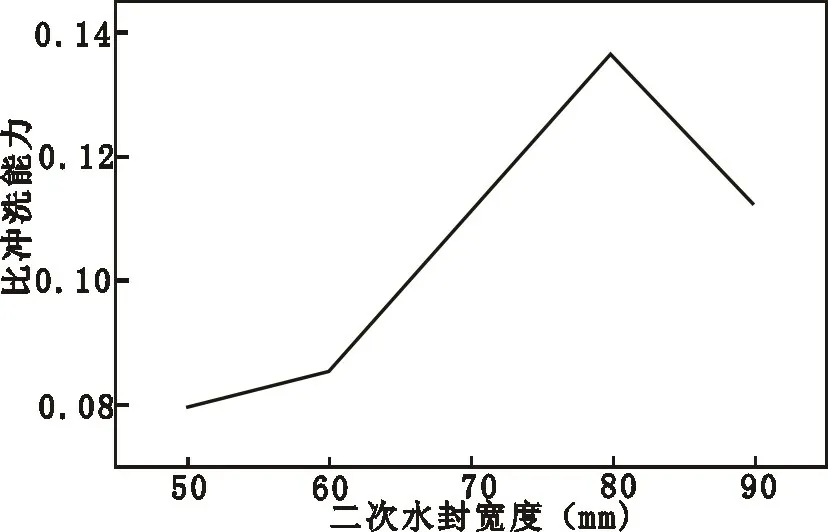
圖4 二次水封寬與比沖洗能力的實驗結果

3.2 曲率寬對沖水性能的影響

當曲率寬度過小時會造成豎直沖洗過程太短,勢能積攢不足而造成一定堵塞,雖然有效減少了第一次沖水消耗的能量,但同時也使第一次沖水末尾攜帶能量較少的水殘留,第二次沖水能量又較小,因此容易造成較嚴重的堵塞。同時從圖5可以看出在曲率寬大約為50 mm 的時具備最大的比沖洗能力。

圖5 曲率寬與比沖洗能力的實驗結果

3.3 傾斜坡度對沖水性能的影響

從本組實驗來看,一次水封的傾斜坡度對沖洗性能的影響也較大。分析原因發現:傾斜坡度過小會導致水沖小球時,在通過一次水封時運動路程較長,消耗多余的能量。當坡度過大時,第一次沖水的效果會大打折扣且造成一定堵塞,再進行第二次沖水時便毫無效果。從圖6可以看出當傾斜坡度為45°時,比沖洗能力達到最大,同時當傾斜坡度增大時,比沖洗能力明顯降低。

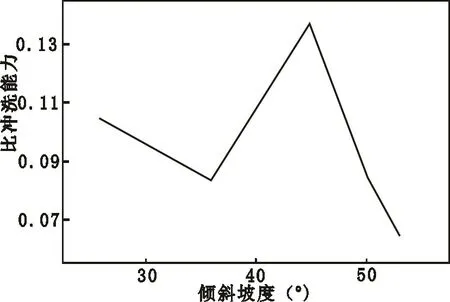
圖6 傾斜坡度的實驗結果

4 虹吸管道沖洗性能參數尋優

4.1 設置正交試驗表

通過對實驗結果進一步分析得出各個因素對實驗影響的重要程度,劃分出主次因素.A 為曲率寬,B 為傾斜坡度,C為二次水封寬,D為二次水封高。表5中,L9(34)為正交表的記號,正交的符號可表示為Ln(rm),其中L 為正交代號,n表示正交表行數,r表示因素水平位置,m 為正交表縱列數。

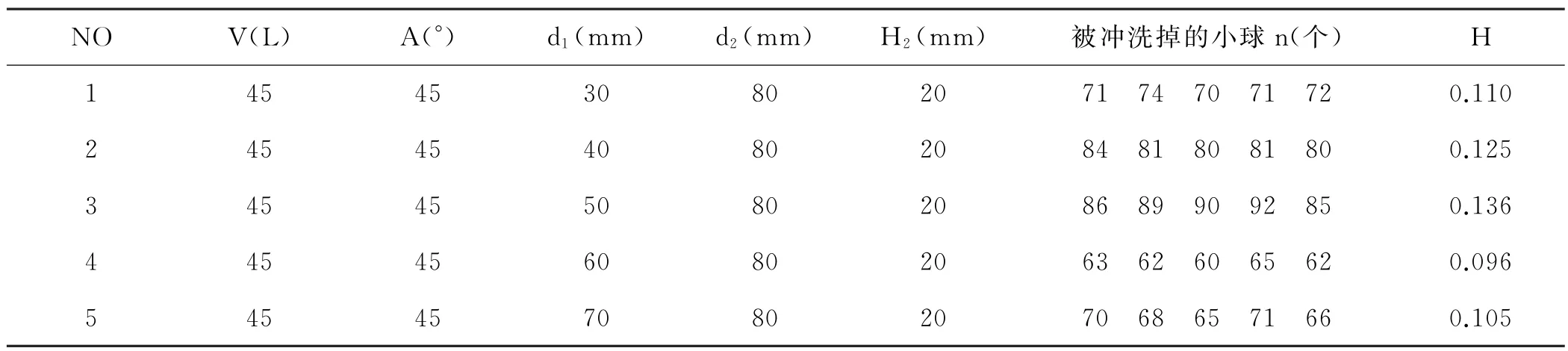
表3 曲率寬的實驗設置

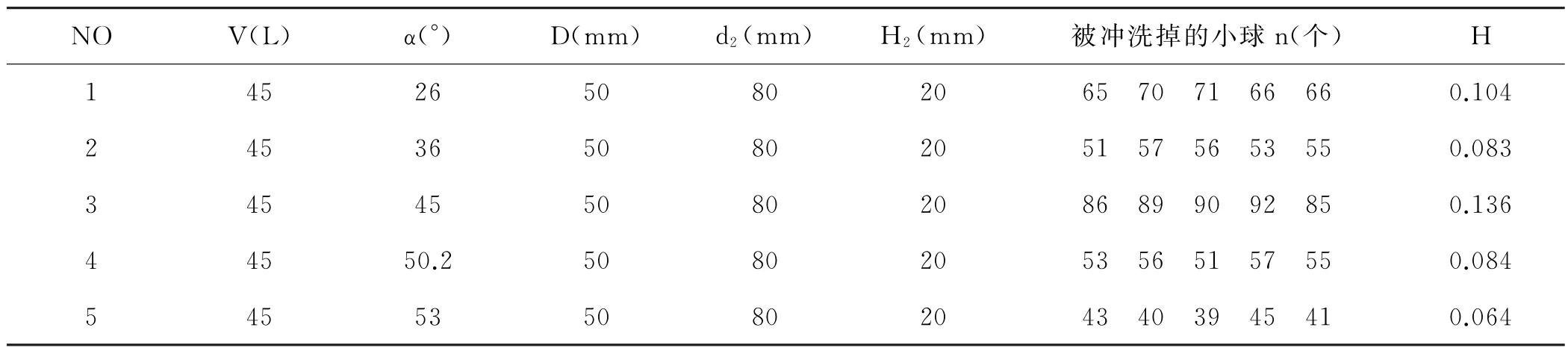
表4 傾斜坡度的實驗設置

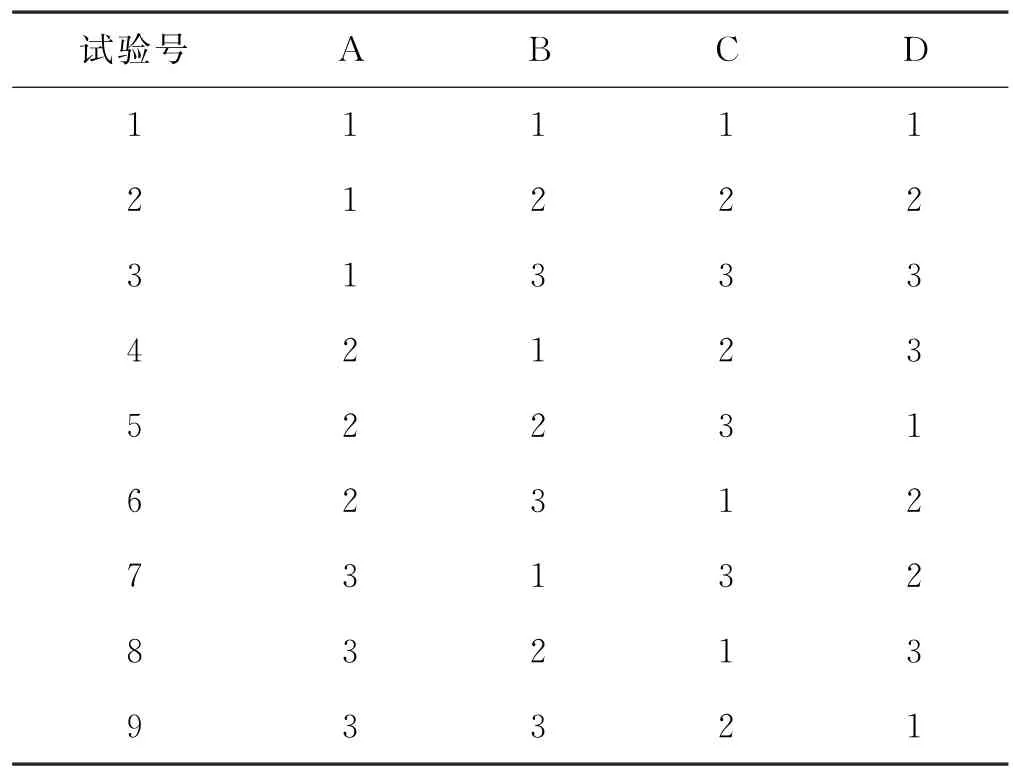
表5 正交表L 9(3 4)

4.2 優方案的確定

優化方案是指在實驗范圍內找到各因素的最佳組合水平。最佳水平的確定取決于實驗指標。當指標越高越好時,應選擇使指標最大化的水平,即各列Ki中最大值所對應的水平。相反,當指標越低越好時,應選擇使指標最小化的水平。Ki:表中某一列的水平編號為i(在表5中i的取值為1、2或3)時,計算該列實驗結果的總和。

R:在每一列中,將R=Max{K1,K2,K3}-Min{K1,K2,K3}定義為極差,極差最大的一列即為對實驗結果產生最大影響的因素水平,也是主要因素。

根據表6設計的正交表所計算出的極差,可直觀地看出二次水封高在這次實驗中為主要因素。二次水封寬與傾斜坡度這2個因素對于實驗也有較大影響,曲率寬對實驗的影響較小。

表6 正交實驗的實驗設置

影響因素的主次關系為D＞C＞B＞A,A 因素列:K2＞K1=K3;B因素列:K1＞K2＞K3;C因素列:K3＞K2＞K1;D 因素列:K1＞K2＞K3,所以優方案為:K2,K1,K3,K1,即曲率寬度50 mm,傾斜坡度36°,二次水封寬為90 mm,二次水封高為10 mm。

圖7為優化后的管道形狀,為進一步驗證正交試驗所得結果的可靠性,根據上表7選擇出來的4個因素的最優數據,計算比沖洗能力后發現通過正交試驗得出的優化數據而得到的結果確實為上述所有實驗中效果最好的一組。

表7 優化方案的實驗設置

圖7 優化后的管道形狀圖

4.3 響應面分析

通過各因素對變量的影響得出其顯著性,同時還可以根據多因素之間的交互作用對對個變量進行分析,從而進行響應曲面優化。對傾斜坡度(B)、二次水封寬(C)、二次水封高(D)3個影響比較大的因素對虹吸管道的比沖洗能力進行響應面分析。

表8為回歸模型方差分析,通過方差分析,發現自變量B、C的系數均顯著不為0,說明二次水封寬度和二次水封高度兩個因素對比沖洗能力的解釋程度較高,對比沖洗能力的變化具有更高的影響。而傾斜坡度對比沖洗能力的變化影響較小。分析結果顯示,F統計量的值較大,表明模型的擬合程度較為良好。決定系數R2=0.9863,說明實際值和預測值之間具有較高的相關性。

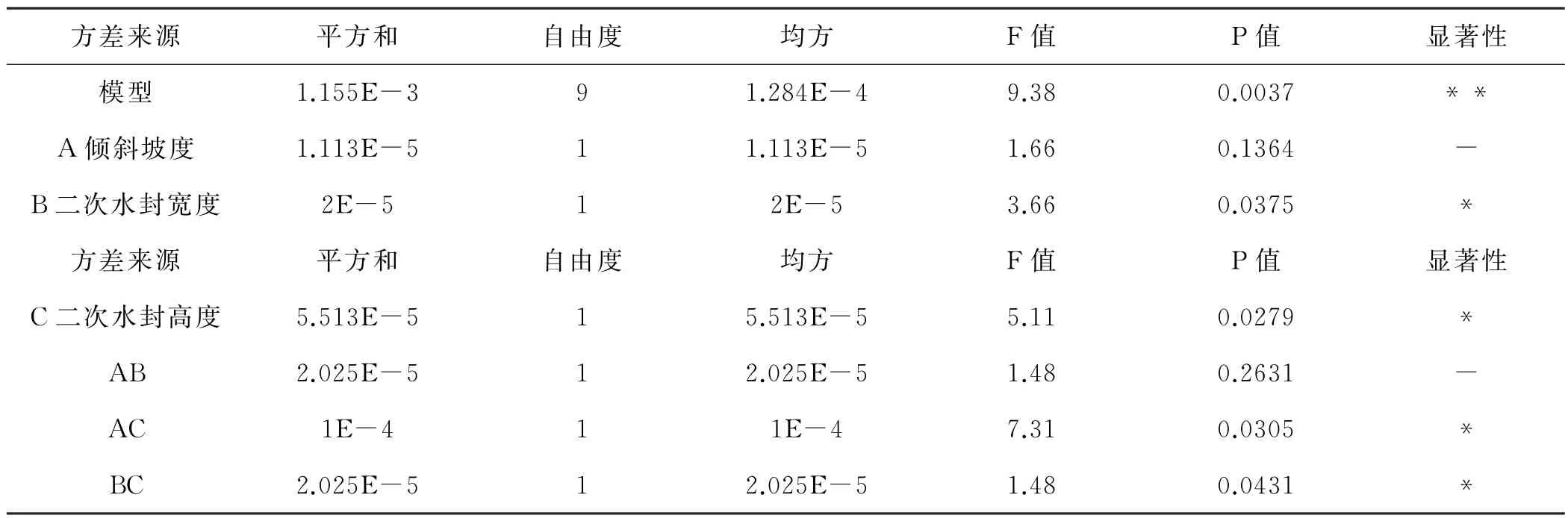
表8 回歸模型方差分析

續表8

圖8為各個因素對比沖洗能力的交互作用,可以看出,各個因素之間的交互作用對虹吸管道比沖洗能力的影響并不完全一樣。圖a中可以看出,比沖洗能力與傾斜坡度和二次水封寬度呈現凸函數關系,傾斜坡度一定時,隨著二次水封寬度的增加,比沖洗能力先增大后減小;當二次水封寬度一定時,隨著傾斜坡度的增大,比沖洗能力先增大后減小;在二次水封寬度為60～80 mm 時,比沖洗能力敏感程度較高。圖b中可以看出,傾斜坡度與二次水封高度對比沖洗能力的交互作用比較復雜,傾斜坡度在26°～35°和二次水封高度在25～40 mm 范圍內,比沖洗能力變化較為劇烈。圖c中可以看出,二次水封寬度與二次水封高度之間存在明顯的交互作用,在二次水封寬度為60～80 mm范圍內,比沖洗能力變化較為劇烈。

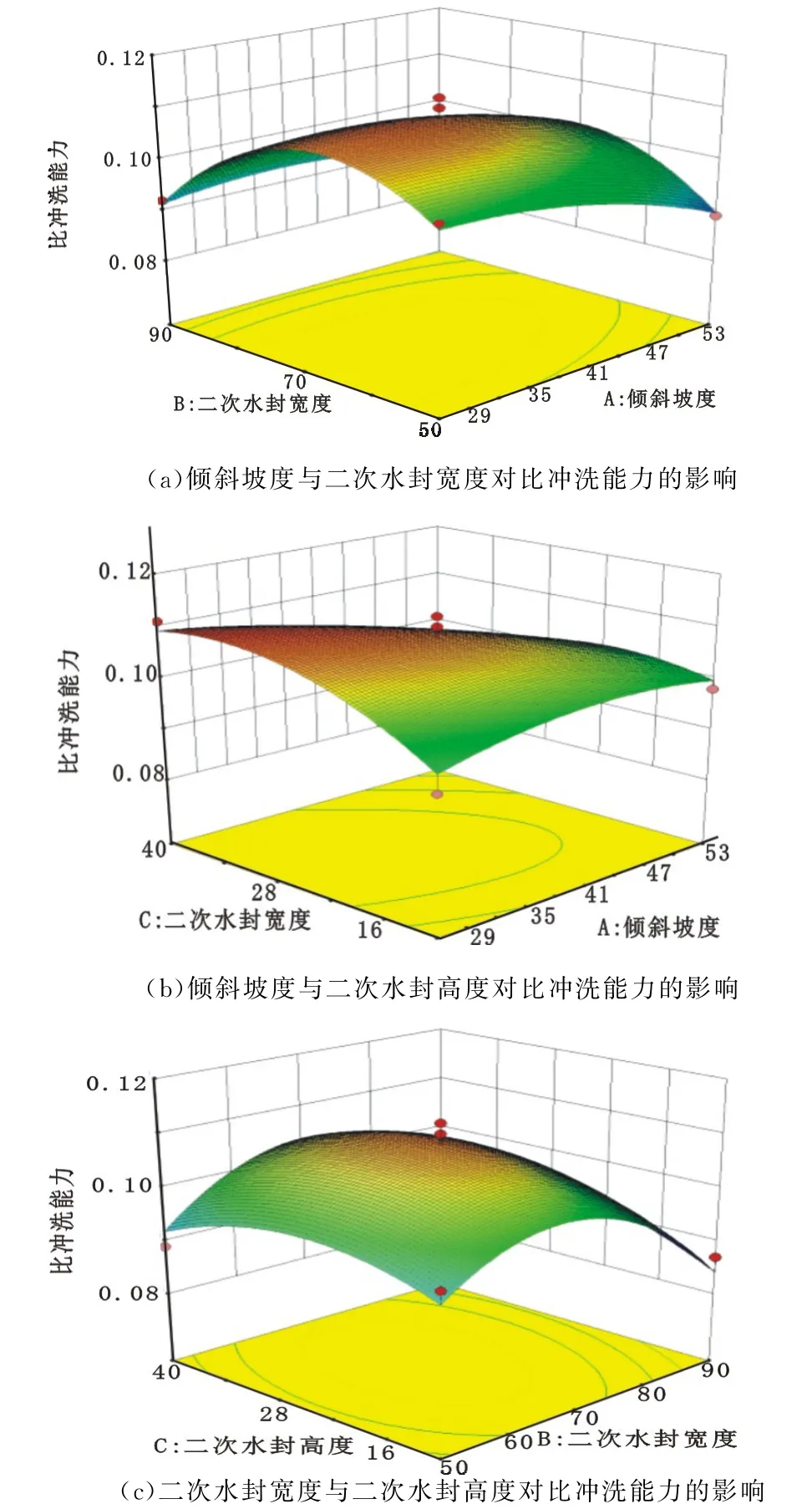
圖8 各個因素對比沖洗能力的交互作用

5 結語

本次研究以優化虹吸管道從而達到節水效果為目的,展開實驗研究。筆者引入比沖洗能力這個概念用以判斷馬桶的沖洗效果。首先采用單因素試驗方法確定較為準確的實驗參數,進而采用正交試驗方法確定主次因素(D為二次水封高＞C為二