考慮動態效應的隧道“零刷坡”頂進法進洞施工全過程數值模擬*

董北毅,高新強,3,4,馬澤騁,樊浩博,朱正國,4

(1.石家莊鐵道大學省部共建交通工程結構力學行為與系統安全國家重點實驗室,河北 石家莊 050043;2.石家莊鐵道大學土木工程學院,河北 石家莊 050043; 3.河北省交通工程結構力學行為演變與控制重點實驗室,河北 石家莊 050043; 4.河北省金屬礦山安全高效開采技術創新中心,河北 石家莊 050043)

0 引言

在工程設計中,數值分析通常被用于工程力學行為模擬。目前,數值模擬頂進法主要有3種,分別為:①采用逐步開挖、添加接觸、激活管節的方式模擬頂進過程,未考慮頂進過程的動態效應[1-6];②考慮頂進過程對土體的擾動,先釋放一部分掌子面周圍應力,再進行開挖和管節激活[7-8];③考慮動態效應,先開挖再添加接觸,施加位移、力或速度荷載模擬頂進過程[9-15]。

在模擬頂進過程的動態效應時,多采用的是小位移頂進,用小位移頂進結果擬合出長距離頂進結果[10,13],實際頂進長度僅為0.05,0.1m。頂進法進洞全過程動態頂進模擬分析幾乎未涉及。

隧道進洞施工過程中,多采用的是刷坡進洞,生態環境較脆弱地區可能需很長時間恢復,如某些隧道洞口地形、地貌復雜,生態環境十分敏感、脆弱[16]。本文提出手掘式頂進法進洞,洞口與水平面呈一定角度,即“零刷坡”進洞,不僅可降低進洞施工對環境的影響,而且可與后續隧道施工工法進行較好銜接。本文對這種“零刷坡”頂進法進洞進行動態數值模擬分析,初步論證其可行性。

1 數值模型建立與參數設置

1.1 基本假定

在實際工程中,頂管施工地質條件復雜,施工工藝、技術水平均會影響頂進法的力學行為,為使數值模擬分析可行作以下假定:①土層設置為單一土層,忽略土體表面凹凸性;②只考慮重力作用下的地應力初始平衡;③假設土體都是連續、均勻、各向同性的彈塑性體,不考慮節理、層理等地質軟弱面;④假設模型物理力學參數在整個計算過程中保持不變,即土體的變形致密作用不予考慮;⑤不考慮頂管接頭的影響。

1.2 有限元模型建立

采用ABAQUS軟件建立三維有限元模型,如圖1所示。頂管管節斷面為馬蹄形,壁厚0.5m,內輪廓如圖2所示。土體底面約束豎向位移,四周約束水平位移,頂管約束底部豎向位移和對稱面水平位移。土體與頂管均采用8結點六面體單元(C3D8R)模擬。模型邊界選取距離隧道中心3倍洞徑。

圖1 三維數值模型(單位:m)

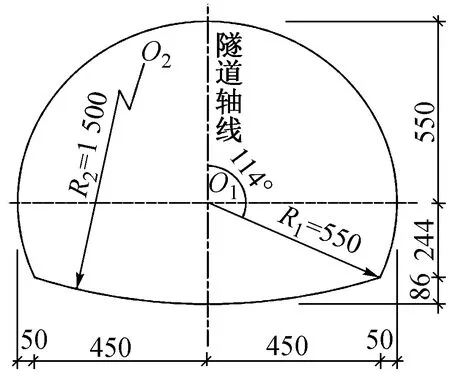
圖2 隧道斷面(單位:cm)

1.3 計算參數選取

參考某頂管工程[14]土體參數及不同潤滑條件下管土摩擦系數,如表1,2所示。聚合物為超級聚丙烯酸,增塑劑為硅酸鈉和聚丙烯酸酯的結合物。土體采用莫爾-庫侖本構模型,注泥漿減摩效果用不同管土摩擦系數模擬,頂管采用C50混凝土,不考慮混凝土塑性變形。

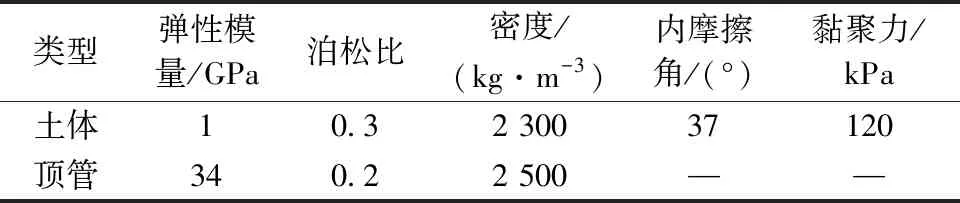
表1 模型物理力學參數

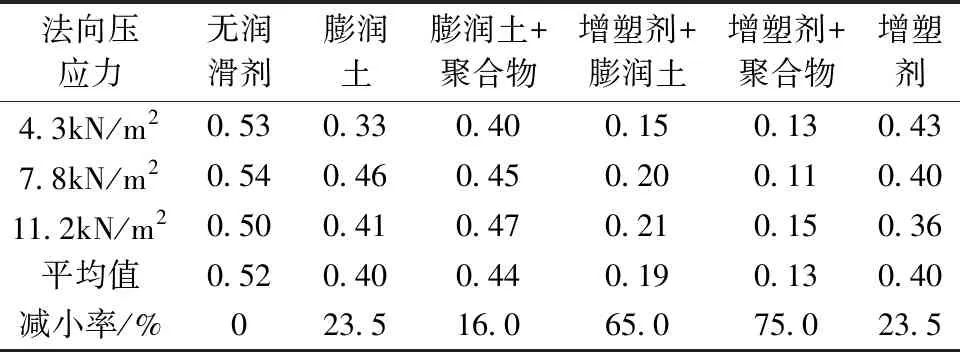
表2 不同類型潤滑劑摩擦系數

隱式分析(靜力學)中管土采用共節點的接觸方式,即兩者變形協調同步;顯式分析(動力學)中管土采用面-面接觸,法向采用“硬接觸”,切向采用罰函數的庫侖摩擦接觸。

1.4 施工階段模擬

在實際工程中,更關注的是頂進速度與頂進距離對力學行為的影響,在隱式分析中施加速度荷載并不容易,一般采用的是先開挖再激活管節的模擬過程,不能對動態頂進過程進行較好模擬。采用顯式分析可較好地模擬動態過程,即在頂管上施加一定速度、位移荷載頂進管節。

地應力平衡后,顯式分析和隱式分析模擬實現方式如下。

顯式分析中,模擬步驟為:首先開挖頂管前方土體,然后給頂管施加頂進方向位移邊界條件(位移控制法[5]),當頂管以一定速度頂到預定位置后,頂管速度變為0,接著開挖下一層土體,頂管繼續頂進。重復上述過程,直到頂管頂到預定深度,完成整個進洞過程。在土體開挖過程中,使用基于時間和空間的單元刪除算法解決ABAQUS顯式分析不能模擬土體開挖的問題,流程如圖3所示。

圖3 基于時間和空間的單元刪除算法流程

需要指出的是,如果采用真實的頂進速度模擬頂進過程,首先計算機性能很難滿足要求,再者由于顯式分析從當前狀態下的可用數據計算新狀態的特性,計算機的舍入誤差將會對計算結果產生較大影響,模擬結果會有較大誤差。所以采用位移-時間曲線控制頂進速度,對真實頂進速度進行折減,選取合適的速度模擬,如果在整個模擬過程中,模型的動能與內能的比值<5%,那么就認為頂進速度對結果的影響很小[17],也就是說可用較大頂進速度模擬真實的頂進過程。本文所采用的頂管頂進位移-時間曲線如圖4所示,平均頂進速度為0.5m/s,共頂進10次,每次頂進2m。

圖4 頂管頂進位移-時間曲線(頂進3次時)

在隱式分析中,模擬步驟為:首先開挖頂管前方土體,然后激活管節,接著開挖下一土體,激活管節,重復上述過程,直到頂管頂到預定深度,完成整個進洞過程。

2 隱式分析與顯式分析結果對比

對比模型物理力學參數完全相同,埋深15m,坡面與水平面夾角45°。模型總動能與總內能比值(KE/LE)如圖5所示,最大值約為1.5%,最小值約為0。

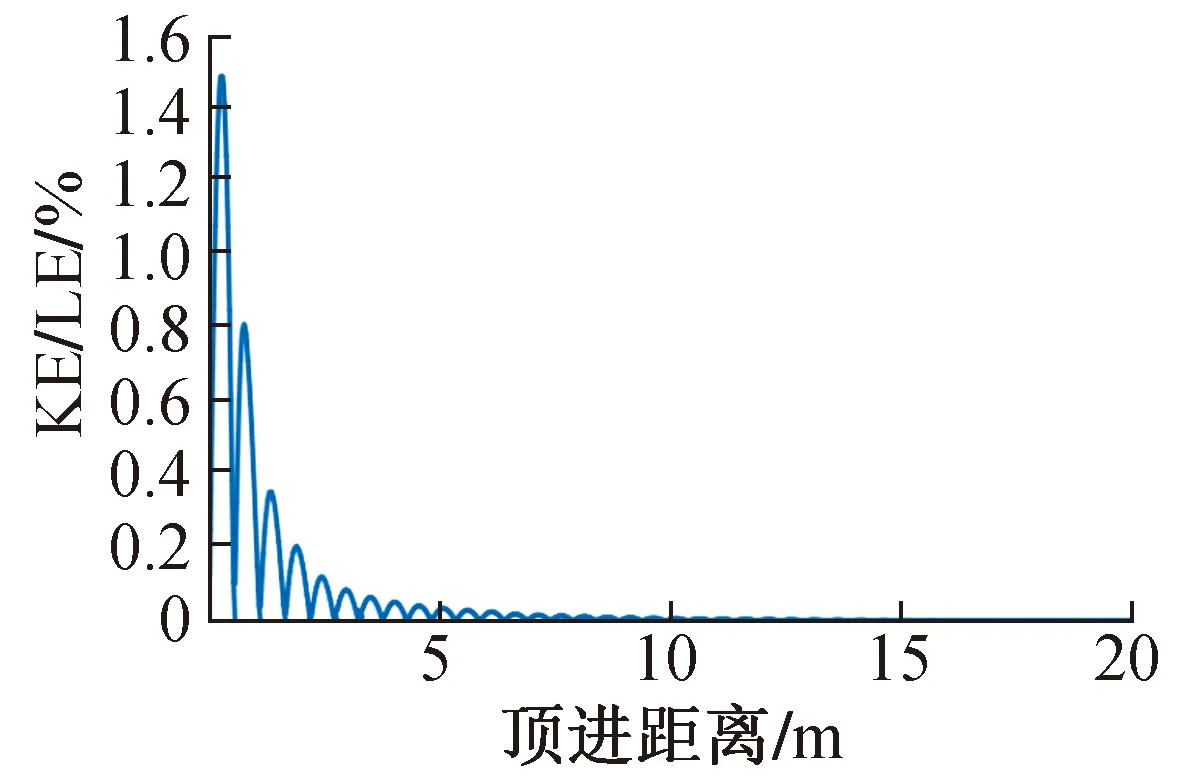
圖5 頂進距離與KE/IE(動能/內能)曲線

分別對比2種方法的Mises應力場、位移場、塑性區及掌子面擠出變形,如圖6～10所示。

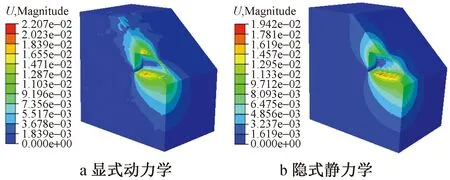
圖7 土體位移(單位:m)

由圖6,7可看出,2種方法的土體Mises應力分布和土體位移分布差異不大,可認為一致。

由圖8可看出,顯式分析的塑性應變比隱式分析的大,且分布在洞口和洞底,這是由于在頂進過程中管土間具有剪切作用,且土體的抗剪強度較低,所以塑性應變較大,從此角度考慮,顯式分析的塑性區結果要優于隱式分析。

由圖9可看出,2種方法的掌子面最大擠出變形(取距洞口14m處掌子面)均在約5.5mm,差距約為6%。

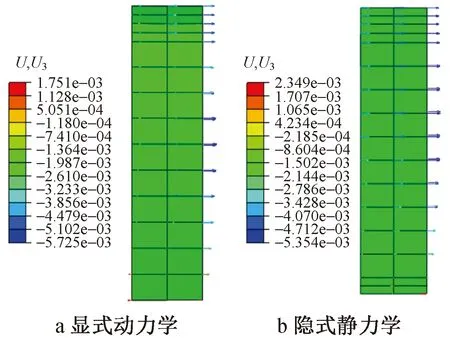
圖9 掌子面擠出變形(單位:m)

由圖10可看出,顯式分析頂管應力要明顯大于隱式分析,且遠遠超過頂管材料的強度,說明頂管已發生破壞。但根據實際工程經驗看,頂管并未發生破壞,這是由于在顯式分析中使用了較大的速度荷載,管土間有沖擊作用,導致頂管應力偏大,所以頂管應力分析應采用隱式分析方法。

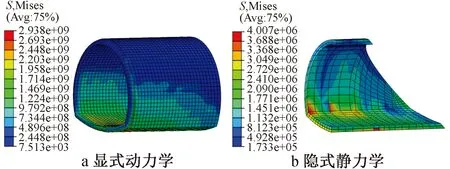
圖10 頂管Mises應力分布(單位:Pa)

綜上所述,采用顯式動力學方法進行頂進法進洞模擬可行,但進行頂管應力分析時需采用隱式靜力學方法。

3 顯式動力學方法頂進力結果分析

對顯式動力學方法進行了進一步模擬,分別模擬了無減摩措施、最優減摩措施、不同坡度和不同管土接觸范圍下的工況,如表3所示。

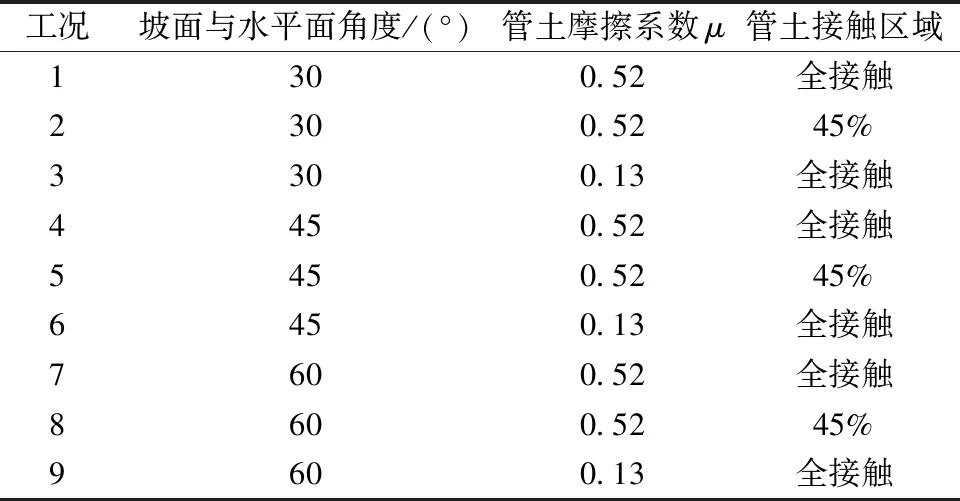
表3 顯式動力學方法模擬工況

各工況模型總動能與總內能比值(KE/LE)趨勢如圖11所示,隨著頂進距離的增大,模型總動能與總內能比值逐漸趨于0,最大值均未超過3%。

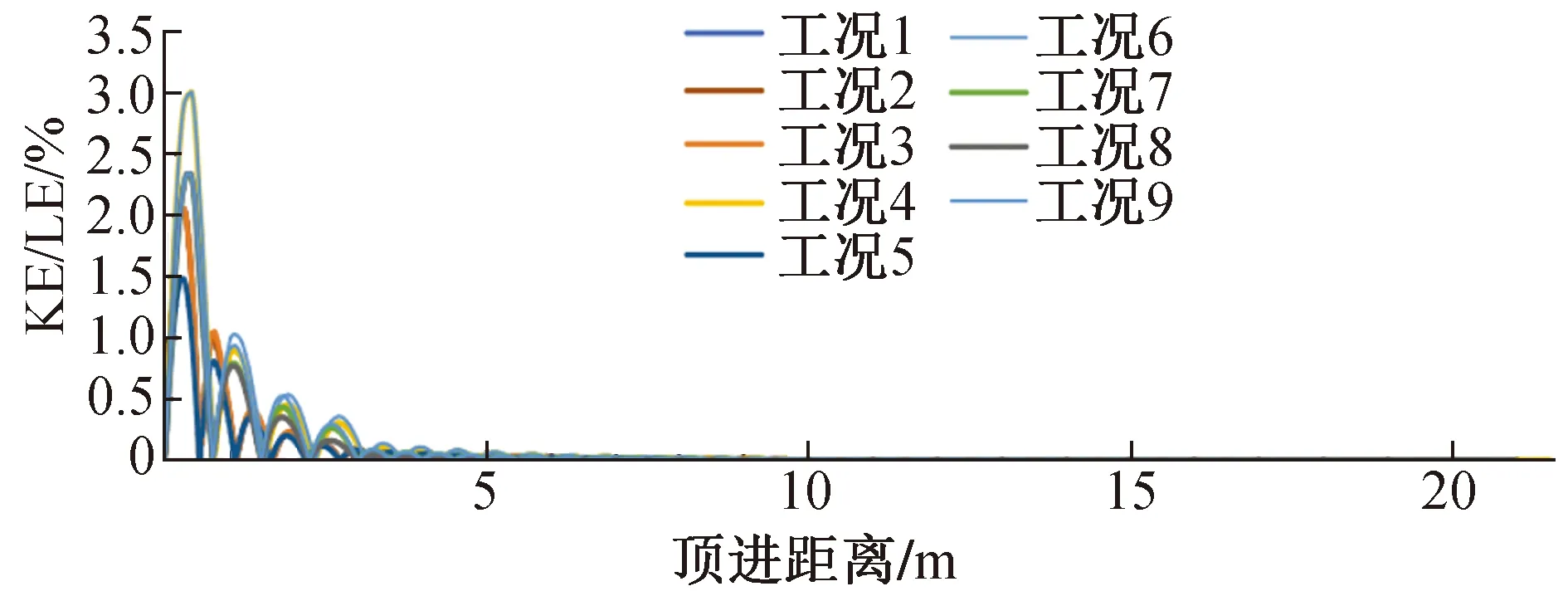
圖11 各工況模型KE/LE趨勢

3.1 頂進力分析

數值模擬計算得出的各工況頂進力與頂進距離關系如圖12所示,取每個“波峰”極值,并忽略突變值,得到頂進力與頂進距離關系曲線,如圖13,14所示。

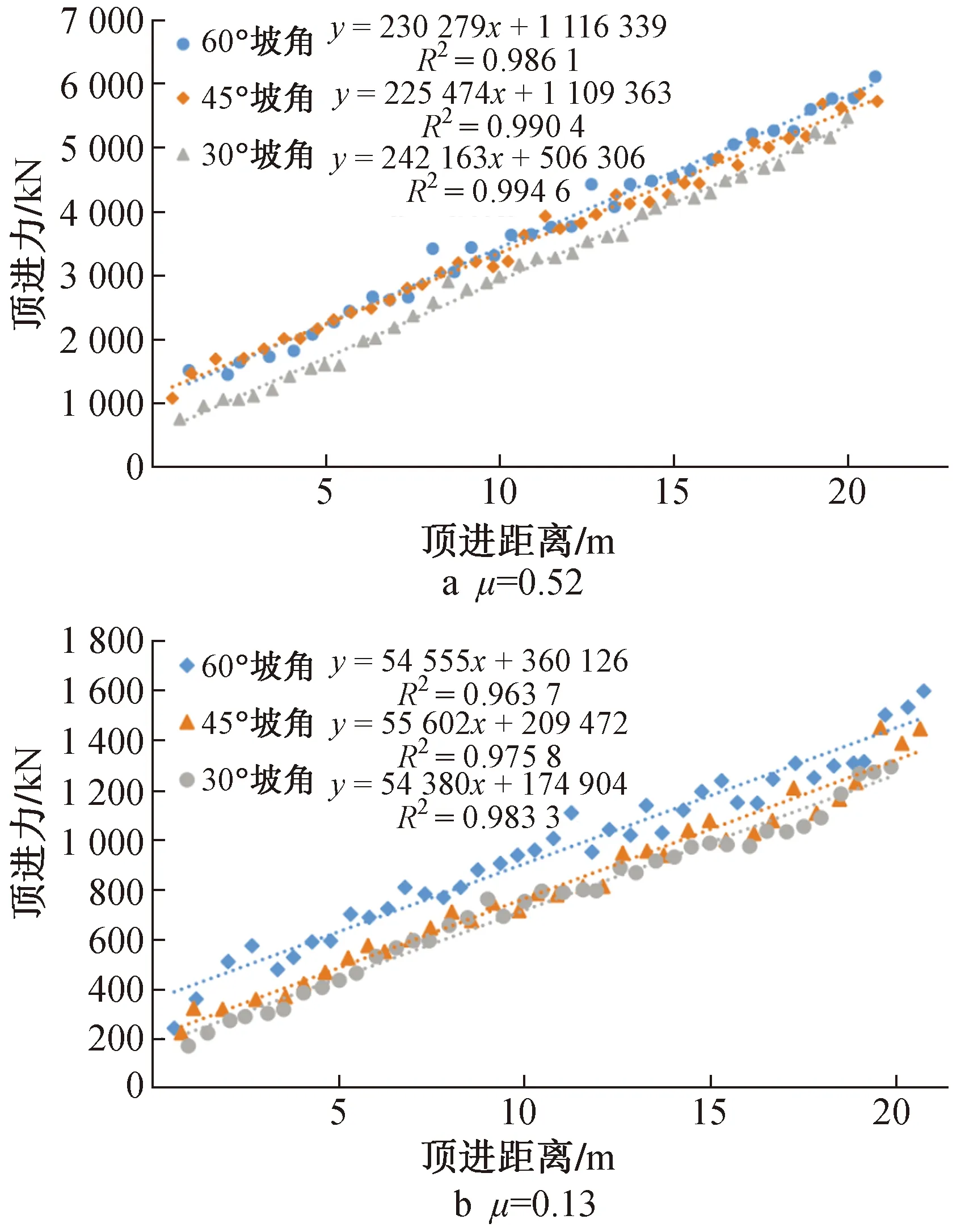
圖13 全接觸工況頂進力與頂進距離關系曲線

圖14 45%管土接觸工況頂進力與頂進距離關系曲線(μ = 0.52)

根據模擬結果,在頂進開始階段,頂進力與頂進距離關系呈現一定的非線性,這與進洞開始階段管土接觸面積增量為非線性吻合。頂管完全被圍巖覆蓋后,頂進力與頂進距離關系轉變為近似線性。相同頂進距離下,洞口坡角與頂進力關系為正相關,即隨著坡角的增大頂進力也隨之增大。

增塑劑+聚合物注泥漿減摩(μ= 0.13)效果明顯。以60°坡角為例,管土全接觸無減摩措施、增塑劑+聚合物減摩頂進20m所需頂進力為5 722,1 451kN, 減摩后頂進力減少約75%。考慮到頂進法進洞頂進距離較短,不進行注泥漿減摩頂進20m所需頂進力不大,結合經濟性和施工效率,可考慮不進行注泥漿減摩。

3.2 管土45%接觸與全接觸頂進力對比

如圖15所示,從頂管應力分布反推管土接觸范圍,管土接觸范圍約在距頂管底部3.5m處,所以將管土接觸設置在距頂管底部3.5m以下范圍,此時管土接觸區域約為45%。與管土全接觸工況對比如表4所示(頂進距離按20m計算)。與管土全接觸相比,45%管土接觸范圍的頂進力分別減少24%,21%,14%(30°,45°,60°坡角),76%～86%頂進阻力作用在距頂管底部3.5m以下部分。在施工中,可將千斤頂布置在距頂管底部3.5m以下部分。

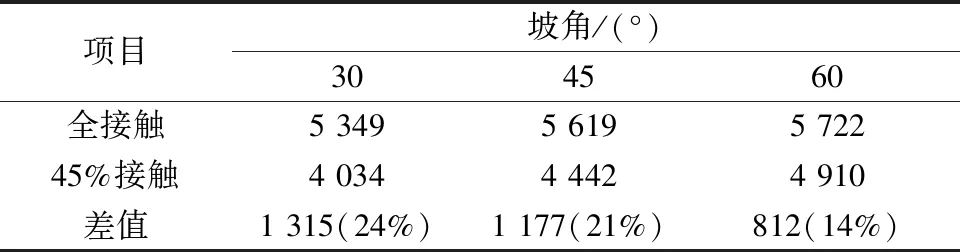
表4 不同接觸范圍頂進力對比

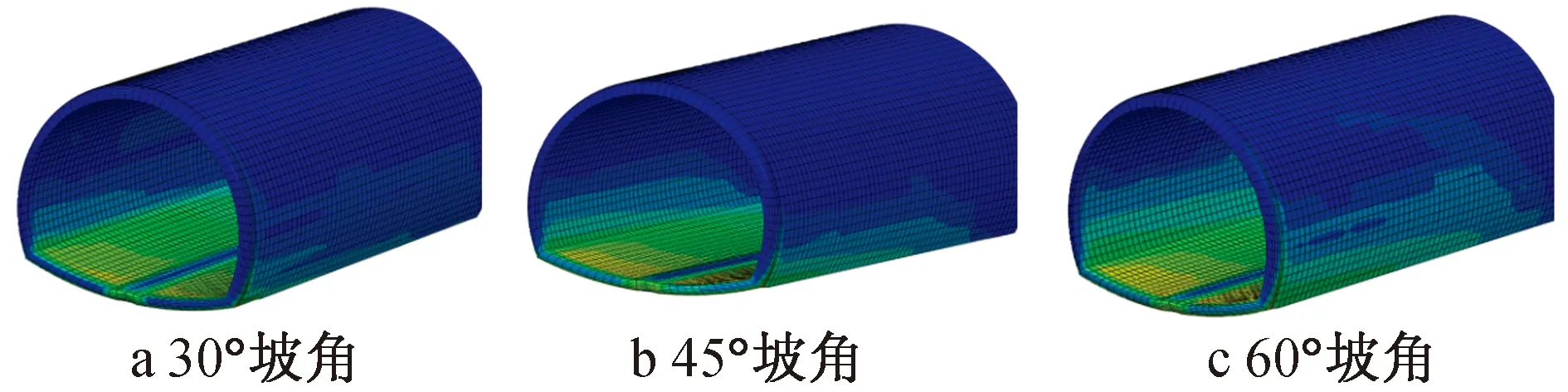
圖15 頂管應力分布

4 頂進力理論公式改進

現有頂進力計算公式均由假設頂管上方覆土深度不變而導出[18-22],對于頂管上方土體為斜面的情況,尚未有理論公式作為參考。參考余彬泉等[18]所提手掘式頂管頂進力理論公式:

F=F0+παBcβqμ′L+παBcC′L+Wμ′L

(1)

式中:F為總頂進力;F0為初始推力(F0= 13.2πBcN′,N′ 為刃口貫入阻力系數);α為管與土的摩擦系數;Bc為管外徑;β為管周邊的荷載系數;μ′為管土間摩擦系數,μ′=tan(φ/2),φ為內摩擦角;q為頂管上方豎向土壓力;C′ 為管土間黏著力;L為頂進距離;W為每米頂管自重。

計算簡圖如圖16所示,假設頂管上方斜向土壓力S與豎向夾角ω滿足ω=(π/2-θ)/(1+L),θ為坡角,當L=0時ω與θ恰好互余。將頂管上方豎向土壓力視為斜向土壓力的豎向分量,相應地在式(1)中加入頂管在斜向土壓力的水平分量作用下的摩阻力,得到改進公式:

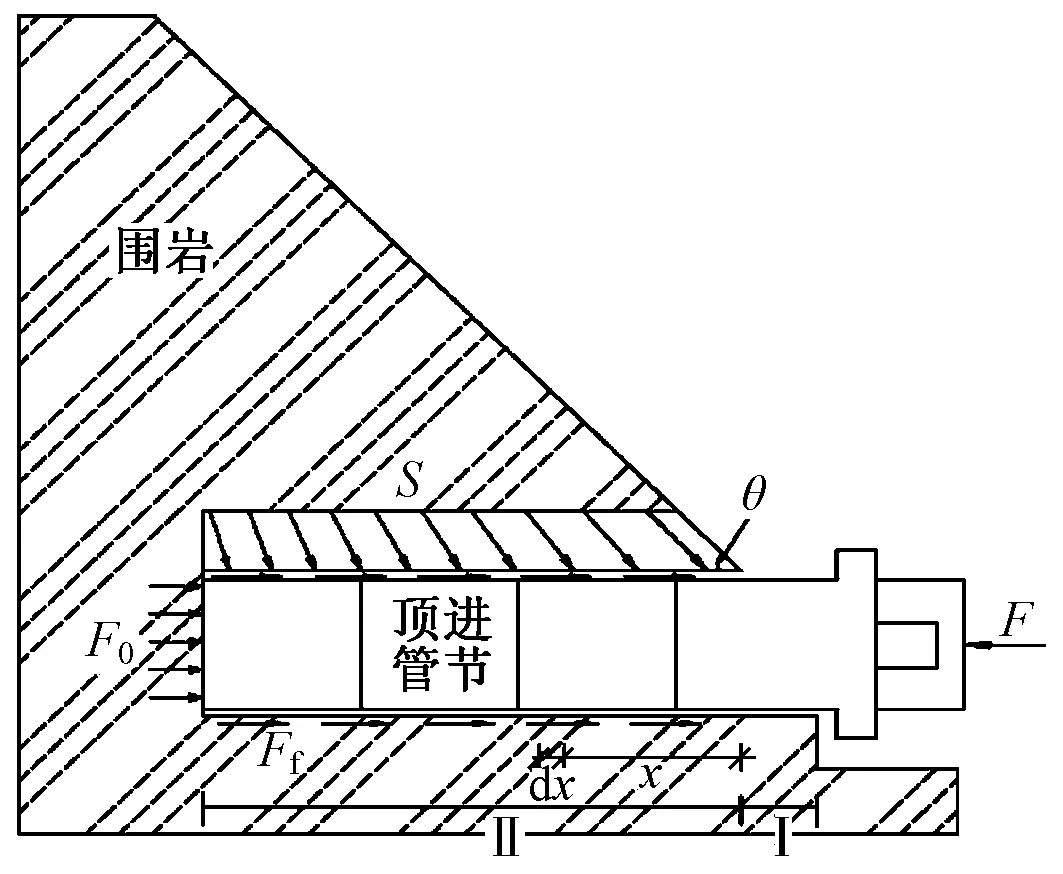
圖16 頂進力計算簡圖

(2)

式(2)即為帶坡度的頂進力計算公式,當豎向土壓力不隨頂進距離變化(埋深不變)時,式(2)退化為式(1)。考慮到豎向土壓力作用范圍過大,對式(2)進一步進行優化,將豎向土壓力作用面積簡化為水平投影面積,得到改進公式:

(3)

改進公式與式(1)對比如圖17所示,式(1)計算結果較大,這與其他學者的結論類似[19]。整體來看各公式頂進力關系為:式(1)>式(2)>式(3)。改進公式大致可分為2個階段:第1個階段為開始頂進到頂管埋深不變,此階段由于頂管埋深隨頂進距離改變、斜向土壓力的水平分量較大,導致頂管上方豎向土壓力隨頂進距離改變,進而頂進力與頂進距離呈現非線性關系;第2個階段為頂管埋深不變到頂進結束,此階段由于頂管上方豎向土壓力不再發生變化,且斜向土壓力的水平分量較小,所以頂進力與頂進距離近似為線性相關。隨著頂進距離的增加,洞口坡度對頂進力的影響逐漸減小,最后近似趨于一致。

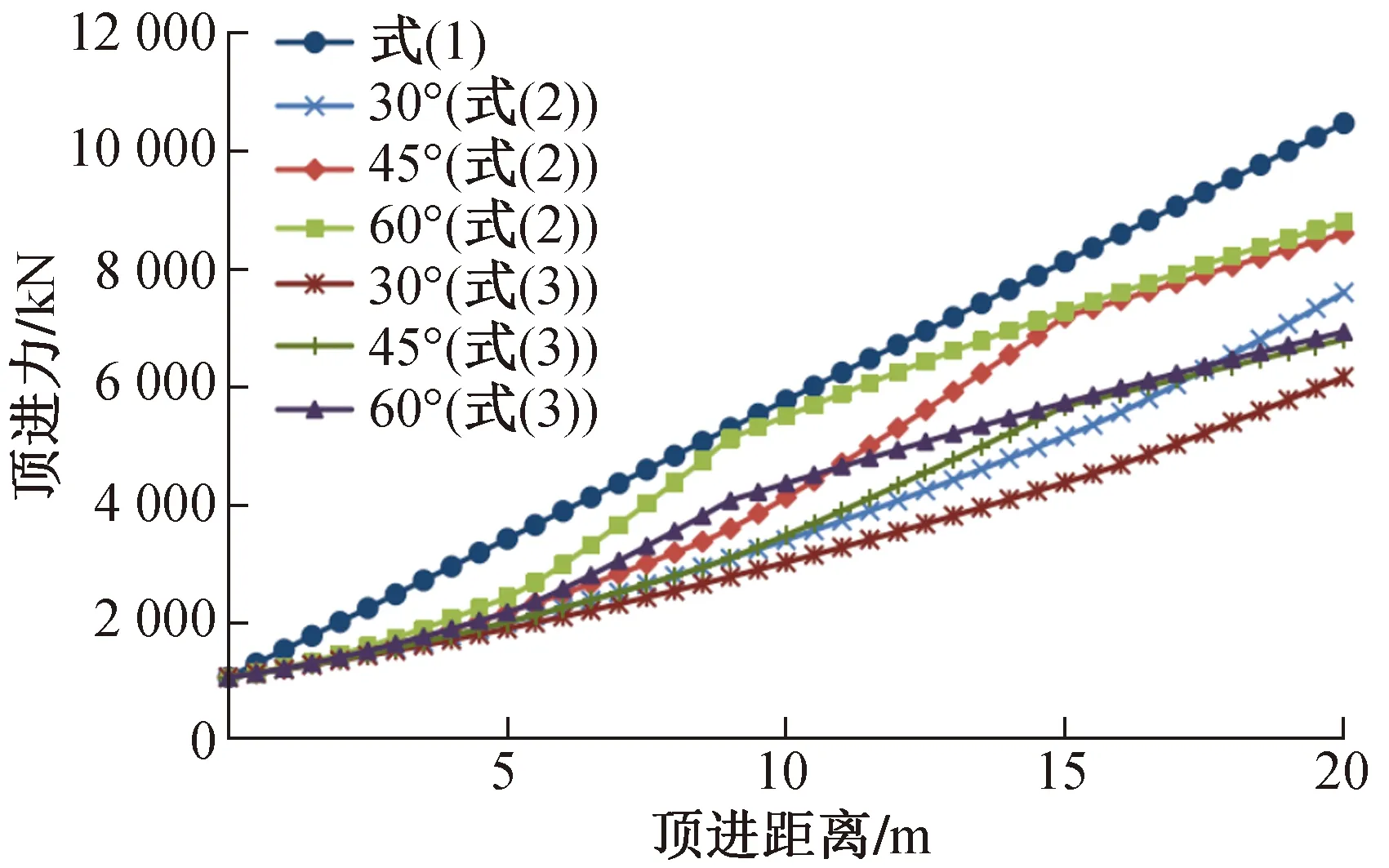
圖17 不同公式對比

理論公式與模擬值頂進力對比(μ= 0.52(全接觸))如表5所示(頂進距離按20m計算),模擬值與式(1)頂進力差值最大,與式(3)頂進力最接近,以60°坡角工況為例,模擬值、式(1)和式(3)頂進20m所需頂進力分別為5 722,10 472,6 931kN,式(1)和式(3)與模擬值差值百分比分別為45.4%,17.4%。

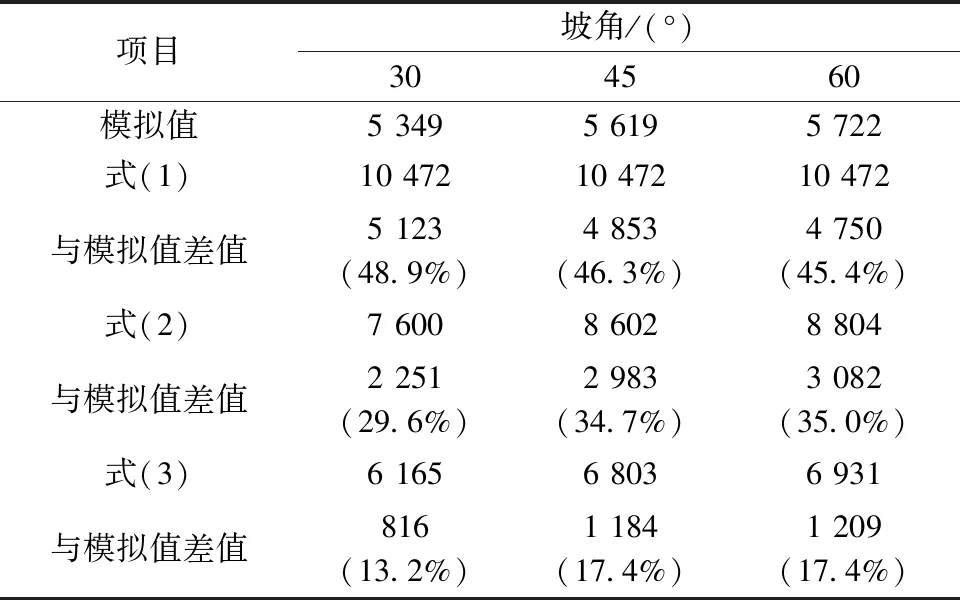
表5 理論公式與模擬值頂進力對比

式(3)較好地反映了洞口坡度對頂進力的影響,且模擬值與式(3)較吻合,說明模擬值較可靠。由于式(1)是在無減摩措施情況下推導,故不與μ= 0.13工況進行比較。

5 結語

1)本文所述顯式動力學模擬頂進法進洞施工方法可行,但進行頂管應力分析時應采用隱式靜力學方法。

2)采用顯式動力學方法,揭示了動態頂進過程中頂進距離對頂進力的影響規律,考慮到頂進法進洞頂進距離較短,不進行注泥漿減摩頂進20m所需頂進力不大,綜合經濟性和施工效率,可考慮不進行注泥漿減摩。

3)推導了洞口帶有坡度情況下的頂進力理論公式,可較好地反映了洞口坡度對頂進力的影響。

4)馬蹄形隧道頂進阻力大部分由頂管下部45%范圍承受。