基于CAT技術的高中數學精準教學策略探索與實踐

林 雄

(福建省福州第二中學,福建 福州 350001)

我國“十四五”規劃提出,要建設高質量的教育體系,促進人的全面發展,并發出了“雙減”的號召.隨著信息技術的發展,如何借力教學輔助系統,利用大數據為不同層次的學生提供精準的、個性化的教學服務是每一位教育工作者無法回避的一個研究課題.

1 基本概念

精準教學[1]是由林斯利(O.R.Lindsley)在斯金納的行為主義理論基礎上提出的,旨在通過對可度量的學習數據的分析與挖掘,對學生的問題進行精準定位,幫助教師制定更具針對性與個性化的教學策略,實現信息技術支持下的精準幫學.

計算機自適應測試(Computerized Adaptive Testing,簡稱CAT)[2]是始于80年代的人機交互學習技術.目前該技術已成為GRE、GMAT等美國、英國、澳大利亞研究生入學考試的核心測評技術.CAT的主要機制是通過算法來實現題目難度的個性化推送.CAT可以在最短的時間內,將每次測試快速收斂至每個學生的最適學習區,為學生提供了“刻意訓練、精熟學習”的高效學習環境.

2 精準教學策略研究的案例介紹

近兩年,我校與福建海峽基礎教育研究院開展合作,依托院方提供的“CAT測量與評價系統”(以下簡稱CAT系統),在高中數學精準教學策略的實踐方面做了一些探索與嘗試,以下是我們的一些實踐案例.

2.1 利用同質化數據,進行同質分組教學,提高教學效率

因為相同的錯誤而產生的數據,我們稱之為同質化數據.比如多選題中漏選或錯選相同的選項,填空題中相同的錯誤答案,等等.按同質化數據對學生進行分組,統一糾錯并輔以CAT系統推送配套練習,可使教學效率有較大提升.

例1 我們在測試投影向量的過程中,通過數據發現大面積的學生這類題準確率都較低.因此我們做了深入了解,發現學生存在的同質錯誤大致分為以下幾類:

(1)把a在b方向上的投影向量與b在a方向上的投影向量混淆.

(2)對公式及公式的變形不熟悉.

(3)對投影向量的方向(或向量的夾角)判斷失誤.

為了能把犯這幾類錯誤的學生篩分出來,我們設計了下列題目:

題1(多選題)a在b方向上的投影可以表示成下列哪些形式?( )

A.|a|cosθe(e為與b同向的單位向量);

B.|b|cosθe(e為與a同向的單位向量);

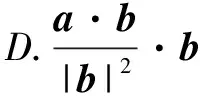
題1答案為:ACD.對于錯選B的學生,歸為同質錯誤1組,引導其發現錯誤的原因為上述第(1)類錯誤.

我們還發現,有時讓同質錯誤組的同學進行小組合作學習,犯同類錯誤的學生更了解相互之間的心理,用他們的話說“更懂得彼此”.有時他們頓悟時蹦出的幾個簡短的字,可以讓同學秒懂,比教師講解的效果更好.這種現象值得我們重視.

2.2 利用差異化數據進行分層次教學,實現因材施教

不同學生由于知識儲備、學習習慣、學習能力、思維水平等方面的差異,在同一課堂單位時間內,學習進度、吸收效果以及能承受的學習難度也不盡相同,這是大班額教學的一大痛點.如何平衡規模化與個性化之間的矛盾?這就需要教師對不同水平層次的學生進行分層次教學.但如何分層次,往往只能依據教師的主觀經驗,缺乏科學性和數據支撐.而CAT系統可以呈現不同維度的測試數據,如測試時長,測試成績,測試題目對錯情況,測試成績變化情況,測試排名變化情況,知識點遍歷完成情況,等等.教師可以根據數據的差異性,對學生進行精準分層,采取有針對性的教學策略,使不同水平層次的學生在原有的基礎上都得到提高.

例2 在考查學生用立體幾何方法求二面角問題時,把學生按照測試成績排名分為4個層次:測試排名在1%～25%為第一層次;測試排名在26%～50%為第二層次;測試排名在51%～75%為第三層次;測試排名在76%～100%為第四層次.在課堂上布置如下變式題[3]:

題3 如圖2,在四棱錐P-ABCD中,底面ABCD是正方形,側棱PA⊥底面ABCD,PA=AD,分別求出下列各二面角的大小:

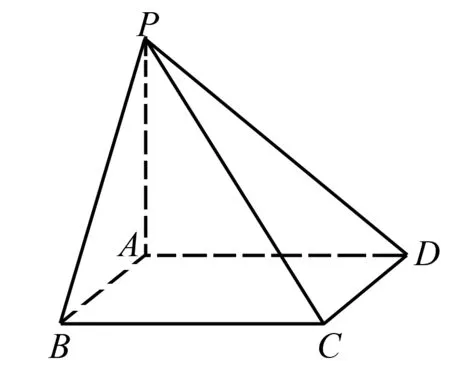
圖2 題3變式題

圖3 題4學生解法示意圖

(1)求二面角P-AB-D的大小;

(2)求二面角B-PA-D的大小;

(3)求二面角P-BC-A的大小;

(4)求二面角B-PC-D的大小;

(5)求二面角A-PD-C的大小;

由縣（區）水利普查辦召集縣級現場復核會，所有縣級普查員、普查指導員參加會議，會上由復核小組說明現場復核的程序。

(6)求二面角A-PC-D的大小;

(7)求平面PAB與平面PCD所成的銳二面角的平面角的大小:(多種解法);

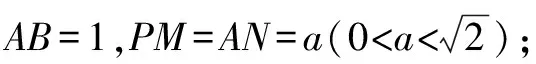
①求MN的長(結果用a表示);

②a為何值時,MN的長最小;

③當MN的長最小時,求二面角A-MN-B的平面角的余弦值

其中(1)(2)兩小題考查二面角的基本作法及直二面角的概念,(3)小題考查線面、線線的垂直關系及二面角的作法,(1)(2)(3)小題都屬于基礎知識與基本技能的要求,適用于第四層次學生;

(7)小題考查無棱二面角的求法,還可要求學生考慮一題多解,如向量解法、補型法或用二面角的余弦值等于射影面積與原面積之比的方法.屬于中等偏上的要求,適用于第二層次學生;

(8)小題考查變量思維、數形結合思想.對直觀想象、邏輯推理、數學運算等核心素養的綜合應用提出了較高要求.適用于第一層次學生.

通過分層教學,對不同層次的學生適配難度與其能力相當的、適量的題目,能夠保證每位學生在自己的“最近發展區”內學有所得.題目與分層學生的問題匹配可以是彈性的,每一分層的學生在完成本層次練習后,如果還有余力,可以完成上一分層的相關問題.這有助于提高其學習的自信心與積極性.

2.3 關注異常化數據,深入挖掘數據表象下的深層次原因

例3在學習已知向量夾角范圍求參數范圍的問題時,我們在相鄰兩周的周練里面分別設置的題4與題5,其中題5作為題4的鞏固性練習.

題4 已知向量a=(1,2),b=(-2,m),若a與b的夾角是鈍角,則( ).

A.m∈(-∞,-2)∪(-2,1)

B.m∈(-∞,1)

C.m∈(-∞,-4)∪(-4,1)

D.m∈(1,+∞)

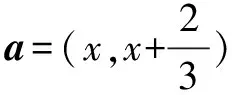
這種解法雖然可行,但是不具一般性.如果a與b中不止一個坐標帶有參數(如題5),原來的方法就不奏效了.當我們精準地找到問題所在,相應的策略也就產生了.

(1)今后再出同類問題的時候,要回避掉可直接用數形結合來解題的題目.更進一步,今后在診斷性練習選題時要盡量選擇可以用通法解決,但是用特法卻不好解決的題目.

(2)從這個問題暴露出,部分學生在聽課習慣上存在缺陷,只要答案正確,就忽略老師的思路講解.借助這個例子可以對這些學生起到很好的教育作用[4].

借助CAT系統,教學中學習行為、學習狀態、學習結果等各類教育信息成為可捕捉、可量化的統計數據,這使教師對學情及教學重難點的把握從“基于經驗”向“基于數據”轉化.通過人機合理分工,功能優勢互補,為學生提供分層、彈性、個性化的訓練內容,使教學策略的制定更加精準有效.以上是我們結合CAT系統,在高中數學精準教學策略方面的一些探索與實踐,希望得到專家與同行們的批評與指正.