蘭州新區現代有軌電車線網布置研究

柴海華

摘 要：通過對國內外城市軌道交通和現代有軌電車線網方案的研究，結合蘭州新區建設現代有軌電車的實際情況，建立基于改進賦權法的VIKOR線路優選模型，利用MATLAB編程求解，得到線路優選模型結果與蘭州新區現代有軌電車線網規劃主推線路一致，驗證了該優選模型的可行性與有效性。

關鍵詞：有軌電車 VIKOR線路 線網布置

1 蘭州新區城市交通現狀與規

蘭州新區位于蘭州、白銀、皋蘭、永登的中央位置，是國家規劃建設的綜合交通樞紐，也是甘肅與外界交流的門戶[1]。蘭州新區周邊和內部都有快速通道，城際鐵路，公共交通通過，交通優勢明顯，但是新區內城市道路較少，分布不均勻，主要集中在中川循環經濟產業園區及其周圍。城市道路單一，公共交通發展緩慢，不便于乘客出行，道路等級低，出行結構不合理[2-3]。

存在的問題：

（1）交通條件整體較差，道路系統匱乏。

（2）公路等級較低，無法滿足與城鎮交通聯系。

（3）公共交通體系不完善，不便于居民出行。

（4）路網體系不健全，不利于城市整體規劃。

2 蘭州新區現代有軌電車應用模式分析

2.1 經典應用模式總結

在美國，有軌電車建設的目的是為了解決都市的擁擠和空氣污染問題。

在澳大利亞，悉尼的有軌電車運輸系統為觀光性質，早已成為當地的特色之一。

法國的有軌電車運輸系統，在主要城市中作為周邊衛星城的連接。

德國有軌電車運輸系統發達，系統發展最為完備。

日本的有軌電車是城市的輔助交通運輸系統。

在我國，有軌電車系統起步比較晚，大部分城市中仍然以私人交通工具和公共交通為主，但是在面臨巨大的交通擁堵，交通癱瘓問題的同時，許多城市已經開始發展了新型有軌電車，為了緩解蘭州新區未來交通擁堵問題，在城市規劃中對蘭州新區建設現代有軌電車有著重大的意義。

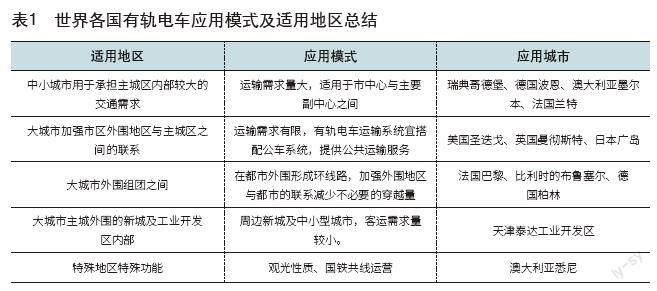
2.2 應用模式種類

3 蘭州新區現代有軌電車線網方案優選

3.1 蘭州新區現代有軌電車線網方案指標值得確定

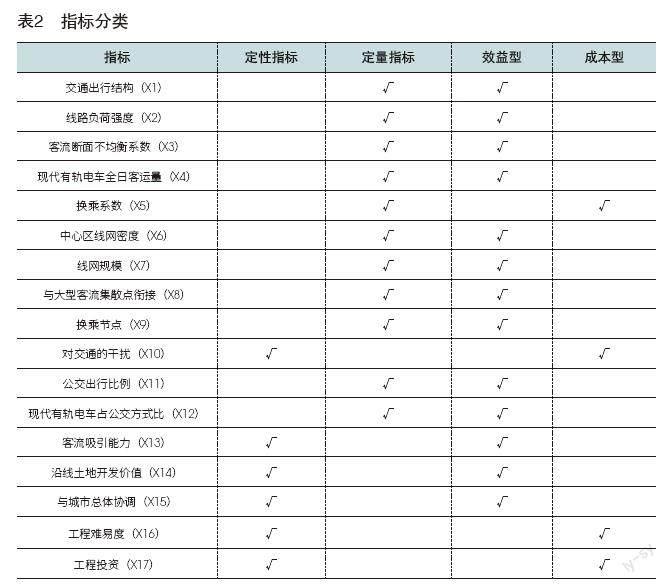
不同的指標在現代有軌電車線網規劃中重要度也不同，在對各指標進行重要度排序之前，首先應當明確指標的分類，根據不同的分類，對指標進行打分，根據投資效益的不同，將影響蘭州新區現代有軌電車線網規劃的指標分為成本型指標和效益型指標兩大類；按指標值是否能夠確定，將影響蘭州新區現代有軌電車線網規劃的指標分為定量指標和定性指標兩大類；具體分類見表2。

定量指標的標準根據線網規劃直接輸入或者通過相關計算可以得到；定性指標通過劃分評價等級，根據蘭州新區現代有軌電車線網規劃項目，蘭州新區的定性指標可以分為四個等級：優、良、中、差，分別對應的分數為10、9、8、7。

3.2 權重的確定

權重的計算全部采用MATLAB編程的方式實現，限于文章篇幅的限制，文章將源程序和部分過程省略。

（1）主觀權重的確定

1）重要度排序

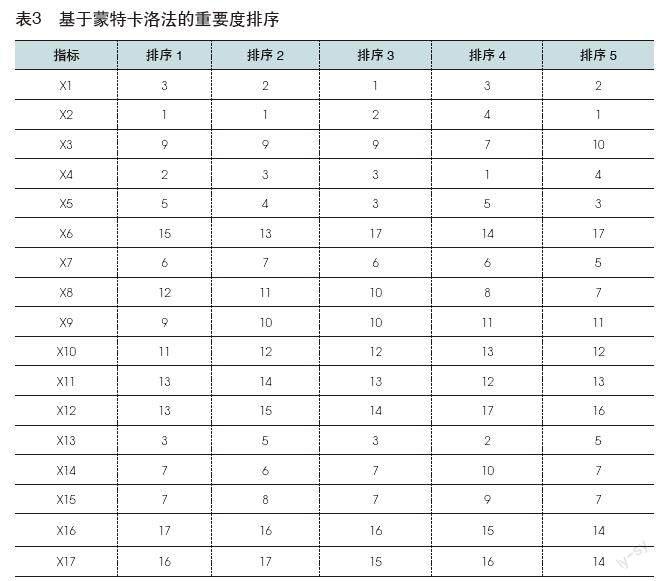
針對蘭州新區建設現代有軌電車的實際情況，對各指標排序如表3：

2）確定試驗次數N

為了盡可能提高計算精度，本文采用0.01誤差小于1%的條件，計算50次，由公式可知N5750，然后進行隨機試驗，可以求得主觀權重。具體見表4。

（2）客觀權重的確定

具體結果如表4所示。

（3）組合權重的確定

組合權重的確定，在計算組合權重時，首先確定重要度系數，分兩種情況：將主觀權重重要度系數取值0.4，客觀權重重要度系數取值0.6；將主觀權重重要度系數取值0.3，客觀權重重要度系數取值0.7；具體計算結果如表4所示。

從上表的結果可以看出，交通出行結構（X1）、線路負荷強度（X2）、換乘系數（X4）、現代有軌電車全日客運量（X5）、線網規模（X7）以及對客流的吸引能力（X13）是比較重要的指標；而與大型客流集散點銜接（X8）、工程難易度（X16）和工程投資（X17）是不太重要的指標。本文采用組合賦權法，將主觀賦權法的重要度系數定為0.3，將客觀賦權法的重要度系數定為0.3。當然在實際應用中，可以根據實際工程的需要，對重要度系數進行調整。

3.3 蘭州新區現代有軌電車VIKOR模型的方案優選

運用VIKOR模型進行線網規劃方案優選的計算全部采用MATLAB計算，限于文章的篇幅，MATLAB源程序省略，各方案的VIKOR計算值如表5所示。

對方案進行優選。

1）基于主觀賦權法的方案優選

由排序條件對方案進行優選：

由排序條件1可知：Ｑ２-Ｑ１=0.4251-0.0439=0.3812，0.3812＜１/（m-1）=0.5，不滿足條件1；由排序條件2可知：S2>S1，則線路2和線路3都為優選線路。

由排序條件1可知：Ｑ3-Ｑ2=1.0000-0.4251=0.5749＞1/（m-1）=0.5，滿足條件1，則線路2為優選線路。

綜上可知：線路3=線路2＞線路1。

2）基于客觀賦權法的方案優選

由排序條件對方案進行優選：

由排序條件1可知：Ｑ2-Ｑ1=0.0668-0.0598=0.0070，0.0070＜1/（m-1）=0.5，不滿足條件1；由排序條件2可知：S2>S1，則線路2和線路3都為優選線路。

由排序條件1可知：Ｑ3-Ｑ2=1.0000-0.4023=0.5977＞1/（m-1）=0.5，滿足條件1，則線路2為優選線路。

綜上可知：線路3=線路2＞線路1。

3）基于組合賦權法的方案優選

由排序條件對方案進行優選：

由排序條件1可知：Ｑ２-Ｑ１=0.2994-0.0000=0.2994，0.2994＜1/（m-1）=0.5，不滿足條件1；由排序條件2可知：S2>S1，則線路2和線路3都為優選線路。

由排序條件1可知：Ｑ3-Ｑ2=1.0000-0.2994=0.7006＞1/（m-1）=0.5，滿足條件1，則線路2為優選線路。

綜上可知：線路3=線路2＞線路1。但考慮到優選線路結果的可靠性、準確性以及實用性，本文推薦使用組合賦權VIKOR模型進行線路優選，所測的結果與蘭州新區主推線路一致，充分驗證了該方法的可行性，對蘭州新區建設現代有軌電車具有指導意義。

4 分析與建議

VIKOR模型在實際應用中比較靈活，權重重要度系數v的取值會影響到Q值得大小，在實際工程應用中，可以根據具體情況對v值進行調整，提高v值，代表決策者更重視群效應最大化，降低Q值，代表決策者更重視最小化，通過調整權重重要度系數v，影響到Q值得改變，進而來分析線路優選結果的改變。隨著重要度系數v的提高，Q值不斷降低，群效益逐漸最大化，就線路2而言，v=0.1時的Q值是v=0.8時的Q值得3倍，VIKOR模型靈活實用，使得評價結果更加趨于實際，得到線路優選模型結果與蘭州新區現代有軌電車線網規劃主推線路一致，驗證了該優選模型的可行性與有效性。

參考文獻：

[1]莫榮韓.蘭州新區現代有軌電車2號線緯一路至中川機場段方案研究[D].蘭州交通大學，2017.

[2]張坤.天水市現代有軌電車線網規劃研究[D].蘭州交通大學，2017.

[3]黃志遠，朱煒，徐瑞華.考慮運營組織因素的現代有軌電車線網規劃方案優化[J].城市軌道交通研究，2017，20（09）：111-115.DOI：10.16037/j.1007-869x.2017.09.023.