一種改進(jìn)雅可比算法的頻域臨界采樣圖濾波器組

李威京,蔣俊正

(桂林電子科技大學(xué) 信息與通信學(xué)院,廣西 桂林 541004)

社交網(wǎng)絡(luò)、傳感器網(wǎng)絡(luò)及腦神經(jīng)網(wǎng)絡(luò)等[1-3]高維不規(guī)則數(shù)據(jù)可建模為圖信號(hào)。與定義在規(guī)則的時(shí)間域與空間域的傳統(tǒng)離散信號(hào)不同,圖信號(hào)通常定義在不規(guī)則的非歐幾里得域。傳統(tǒng)的信號(hào)處理方法不適用于圖信號(hào),如何處理這類(lèi)高維不規(guī)則數(shù)據(jù)已成為一個(gè)亟待解決的問(wèn)題。為此,研究人員提出了圖信號(hào)處理框架[4],該框架將傳統(tǒng)信號(hào)處理方法與圖論相結(jié)合,為處理這類(lèi)高維不規(guī)則數(shù)據(jù)提供了強(qiáng)有力的工具。其中,由傳統(tǒng)濾波器組延伸而來(lái)的圖濾波器組[5-7]因其稀疏特性和多分辨分析能力而受到了廣大研究人員的青睞。

目前,圖濾波器組的設(shè)計(jì)方法主要有頂點(diǎn)域采樣圖濾波器組和頻域采樣圖濾波器組。文獻(xiàn)[8]提出了完全重構(gòu)的兩通道頂點(diǎn)域臨界采樣圖濾波器組,該濾波器組滿(mǎn)足正交特性,但不滿(mǎn)足緊支撐性。文獻(xiàn)[9]提出了雙正交圖小波濾波器組,該濾波組既滿(mǎn)足完全重構(gòu)特性,又滿(mǎn)足緊支撐性。但上述2種頂點(diǎn)域采樣濾波器組本質(zhì)上僅適用于二分圖,對(duì)于非二分圖則需要進(jìn)行近似處理。文獻(xiàn)[10]提出的樣條圖小波濾波器組滿(mǎn)足完全重構(gòu)特性與圖不變性,其對(duì)所有拓?fù)浣Y(jié)構(gòu)的圖信號(hào)都適用。然而,這幾類(lèi)頂點(diǎn)域采樣圖濾波器組還存在如下局限性:1)需要選擇合適的采樣集,才能確保其完全重構(gòu);2)其完全重構(gòu)的采樣集不唯一,不同的采樣集會(huì)影響圖濾波器組的整體性能。文獻(xiàn)[11]提出了兩通道頻域臨界采樣圖濾波器組,該頻域采樣圖濾波器組克服了頂點(diǎn)域采樣圖濾波器的缺點(diǎn),其完全重構(gòu)的采樣集是唯一的,且對(duì)于任意拓?fù)浣Y(jié)構(gòu)的圖信號(hào)都滿(mǎn)足完全重構(gòu)特性;但由于其采樣操作在頻域上進(jìn)行,需要借助特征分解來(lái)獲取圖模型的特征向量矩陣,這導(dǎo)致了計(jì)算復(fù)雜度過(guò)高。

針對(duì)頻域臨界采樣圖濾波器組存在的問(wèn)題,可采用改進(jìn)的雅可比算法(截?cái)嘌趴杀人惴ê筒⑿薪財(cái)嘌趴杀人惴?來(lái)近似求解拉普拉斯矩陣的特征矩陣。改進(jìn)的雅可比算法是一種貪婪算法,其每步迭代所求得的稀疏正交矩陣都屬于Givens旋轉(zhuǎn)矩陣,將每步迭代求得的Givens旋轉(zhuǎn)矩陣相乘,可得到近似特征矩陣,從而近似求得圖信號(hào)的頻域表示。改進(jìn)雅可比算法在滿(mǎn)足完全重構(gòu)的條件下降低了頻域臨界采樣圖濾波器組的計(jì)算復(fù)雜度。

1 基礎(chǔ)知識(shí)

1.1 圖信號(hào)處理的基礎(chǔ)知識(shí)

無(wú)向圖G=(V,E)是由頂點(diǎn)集V={0,1,…,N-1}與邊集E組成,其中節(jié)點(diǎn)數(shù)N=|V|表示圖的大小。圖G可用權(quán)重矩陣W∈RN×N表示,權(quán)重矩陣的元素wij表示頂點(diǎn)i與頂點(diǎn)j之間的關(guān)聯(lián)程度,若wij=0,則表示頂點(diǎn)i與頂點(diǎn)j之間沒(méi)有邊相連。根據(jù)權(quán)重矩陣W,可定義度矩陣D、拉普拉斯矩陣L,度矩陣D是對(duì)角矩陣,其對(duì)角線(xiàn)元素等于權(quán)重矩陣的行和,即,而拉普拉斯矩陣L定義為度矩陣與權(quán)重矩陣之差,即L=D-W。對(duì)拉普拉斯矩陣L進(jìn)行特征分解,有

其中,對(duì)角矩陣Λ∈RN×N的對(duì)角元素由L的特征值組成,其對(duì)角元素按從小到大的順序排列,即0=λ0≤λ1≤…≤λN-1,特征矩陣U=[u0,u1,…,uN-1]的列向量對(duì)應(yīng)于L的特征向量。

圖信號(hào)可表示為N維向量f∈RN,即f=[f0,f1,…,fN-1]T,其中第i個(gè)元素對(duì)應(yīng)于圖上第i個(gè)節(jié)點(diǎn)的信號(hào)值。與傳統(tǒng)離散信號(hào)類(lèi)似,圖信號(hào)也有對(duì)應(yīng)的頻域表示,圖信號(hào)f的圖傅里葉變換定義為

逆圖傅里葉變換定義為

式(2)、(3)稱(chēng)為圖傅里葉變換對(duì)。

圖濾波可從頂點(diǎn)域和頻域2個(gè)角度考慮。在頂點(diǎn)域,圖濾波可表示為拉普拉斯矩陣的多項(xiàng)式,圖信號(hào)的圖濾波過(guò)程可表示為

圖信號(hào)在經(jīng)過(guò)圖濾波后,每個(gè)頂點(diǎn)的信號(hào)值都是其p-hop鄰域的信號(hào)值的線(xiàn)性組合。在頻域,圖信號(hào)的圖濾波過(guò)程可表示為

為圖濾波器的頻率響應(yīng),H(λi)為圖頻率的多項(xiàng)式。

1.2 兩通道頻域臨界采樣圖濾波器組的結(jié)構(gòu)

圖1為兩通道頻域臨界采樣圖濾波器組的基本結(jié)構(gòu)[11],其中:

圖1 兩通道頻域臨界采樣圖濾波器組

兩通道頻域臨界采樣圖濾波器組的輸入輸出關(guān)系為

根據(jù)輸入輸出關(guān)系,當(dāng)子帶濾波器的頻率響應(yīng)滿(mǎn)足

傳遞函數(shù)T=c2I,此時(shí)該濾波器組滿(mǎn)足完全重構(gòu)條件[11]。

關(guān)于G0(λi)、H0(λi)的設(shè)計(jì),現(xiàn)有的設(shè)計(jì)方法主要有正交[8]和雙正交[9]2種類(lèi)型。兩通道頻域采樣圖濾波器組的正交設(shè)計(jì)取決于H0(λi),而H0(λi)的設(shè)計(jì)借鑒了經(jīng)典信號(hào)處理中的設(shè)計(jì)方法[8],即

其余濾波器H1(λi)、G0(λi)、G1(λi)都可由H0(λi)求得,

與此同時(shí),為了確保圖濾波器組的完全重構(gòu)特性,H0(λi)需滿(mǎn)足:

對(duì)于雙正交頻域采樣圖濾波器組而言,其高通濾波器則由低通濾波器定義[9],即

G0(λi)、H0(λi)可通過(guò)頻譜分解獲得。該設(shè)計(jì)方法類(lèi)似于經(jīng)典信號(hào)處理中的雙正交小波變換[13]。在上述條件的約束下,雙正交頻域采樣圖濾波器組的完全重構(gòu)條件[9]為

2 頻域臨界采樣圖濾波器組的快速實(shí)現(xiàn)方法

頻域臨界采樣圖濾波器組需要計(jì)算圖信號(hào)的圖傅里葉變換,因此需對(duì)拉普拉斯矩陣L進(jìn)行特征分解,求得其特征矩陣U,該操作的計(jì)算復(fù)雜度為O(n3)。當(dāng)圖的規(guī)模較小時(shí),可快速求得其特征矩陣,但當(dāng)圖的規(guī)模較大時(shí),計(jì)算特征矩陣U的代價(jià)會(huì)變得較大。為降低求解特征矩陣U的計(jì)算復(fù)雜度,可采用改進(jìn)的雅可比算法來(lái)近似求解特征矩陣U[14]。

2.1 近似求解特征矩陣的問(wèn)題歸結(jié)

近似求解特征矩陣U的目的是找到一個(gè)近似的特征矩陣,使得以下最優(yōu)化問(wèn)題取得最小值:

為了衡量近似特征矩陣與特征矩陣U間的計(jì)算復(fù)雜度,給出相對(duì)復(fù)雜度(relative complexity gain,簡(jiǎn)稱(chēng)RCG)的定義[14]。相對(duì)復(fù)雜度是特征矩陣U的非零元素個(gè)數(shù)與近似特征矩陣中的稀疏正交因子Sj的非零元素個(gè)數(shù)之和的比率,即

其中‖U‖0為矩陣U的0范數(shù)。

2.2 截?cái)嘌趴杀人惴?/h3>

截?cái)嘌趴杀人惴ㄊ茄趴杀人惴╗15]的改進(jìn),雅可比算法在近似對(duì)角矩陣Lj達(dá)到某個(gè)精度后停止迭代,而截?cái)嘌趴杀人惴▌t預(yù)先設(shè)置了迭代次數(shù)。對(duì)于式(12)的最優(yōu)化問(wèn)題,若將稀疏正交矩陣Sj約束在Givens旋轉(zhuǎn)矩陣集RG中,并預(yù)先設(shè)定稀疏正交矩陣Sj的個(gè)數(shù)J,即可得到截?cái)嘌趴杀人惴╗14]。n維向量的Givens旋轉(zhuǎn)固定其中n-2個(gè)坐標(biāo),其余2個(gè)坐標(biāo)則旋轉(zhuǎn)一定的角度,n維Givens旋轉(zhuǎn)矩陣可表示為

其中:p、q為旋轉(zhuǎn)坐標(biāo);θ∈[0,2π]為旋轉(zhuǎn)角;c=cosθ;s=sinθ[16]。顯然,Givens旋轉(zhuǎn)矩陣由p、q、θ三個(gè)參數(shù)所決定。截?cái)嘌趴杀人惴ㄊ且环N貪婪算法,其每步迭代都旨在尋找一個(gè)Givens旋轉(zhuǎn)矩陣,使得代價(jià)函數(shù)下降最快[14],即

截?cái)嘌趴杀人惴ㄈ缦?

輸入:拉普拉斯矩陣,Givens旋轉(zhuǎn)次數(shù)。

輸出:近似特征矩陣,近似特征值。

初始化:Lj=L,j=1。

5) 若err_θ1＜err_θ2,則旋轉(zhuǎn)角θ=θ1;若err_θ1＞err_θ2,則旋轉(zhuǎn)角θ=θ2;

6) 計(jì)算c=cosθ,s=sinθ及Givens旋轉(zhuǎn)矩陣;

7) 計(jì)算Givens旋轉(zhuǎn)后的拉普拉斯矩陣Lj+1=,若j＜J,則返回步驟1),繼續(xù)迭代;若j=J,則終止迭代,且輸出近似特征矩陣=S1S2…SJ,近似特征值=diagLj+1。

2.3 并行截?cái)嘌趴杀人惴?/h3>

式(13)給出的相對(duì)復(fù)雜度增益只是理論上的度量指標(biāo),在實(shí)際運(yùn)算過(guò)程中,使用近似特征矩陣運(yùn)算的時(shí)間開(kāi)銷(xiāo)與其相對(duì)復(fù)雜度增益并不完全成比例。這是因?yàn)?在編程環(huán)境中(如MATLAB),近似特征矩陣=S1S2…SJ與向量相乘是一個(gè)串行過(guò)程,而特征矩陣U與向量相乘則是一個(gè)并行過(guò)程[14]。因此,即使相對(duì)復(fù)雜度增益較大,使用近似運(yùn)算的時(shí)間也可能相對(duì)較長(zhǎng)。

由截?cái)嘌趴杀人惴ǜ倪M(jìn)而來(lái)的并行截?cái)嘌趴杀人惴╗14]較好地解決了上述問(wèn)題。在每步迭代過(guò)程中,截?cái)嘌趴杀人惴ㄖ蛔隽?次Givens旋轉(zhuǎn),而并行截?cái)嘌趴杀人惴▌t可做n/2次Givens旋轉(zhuǎn)。因此,對(duì)于需要進(jìn)行J次Givens旋轉(zhuǎn)的近似過(guò)程,并行截?cái)嘌趴杀人惴ㄖ恍柽x擇K=2J/n個(gè)旋轉(zhuǎn)因子,其中每個(gè)旋轉(zhuǎn)因子Sk都是由n/2個(gè)不相交Givens旋轉(zhuǎn)所組成的矩陣,其數(shù)學(xué)表達(dá)式可表示為

與截?cái)嘌趴杀人惴?lèi)似,并行截?cái)嘌趴杀人惴ㄒ彩峭ㄟ^(guò)尋找矩陣Lk中絕對(duì)值最大的元素來(lái)確定Givens旋轉(zhuǎn),不同的是,所選出的n/2個(gè)元素必須保證兩兩之間不處在同一行或同一列。在每步迭代過(guò)程中,雖然并行截?cái)嘌趴杀人惴ǖ玫降慕獠皇亲顑?yōu)解,但其實(shí)際運(yùn)行時(shí)間要遠(yuǎn)低于截?cái)嘌趴杀人惴╗14]。并行截?cái)嘌趴杀人惴ㄈ缦?

輸入:拉普拉斯矩陣L,Gives旋轉(zhuǎn)次數(shù)J,每次迭代的Givens旋轉(zhuǎn)次數(shù)t=n/2。

輸出:近似特征矩陣,近似特征值。

初始化:Lk=L,k=1。

1) 取拉普拉斯矩陣Lk的上三角元素,并按從大到小的順序進(jìn)行排列;

2) 取前n/2個(gè)最大值元素,且保證兩元素不在同一行或同一列;

3) 根據(jù)取出的n/2個(gè)元素,計(jì)算其對(duì)應(yīng)的Givens旋轉(zhuǎn)角,

4) 計(jì)算ci=cosθi,si=sinθi,并將其填入矩陣Sk相應(yīng)的位置;

5) 若err_q1＜err_q2,則旋轉(zhuǎn)角θ=θ1;若err_q1＜err_q2,則旋轉(zhuǎn)角θ=θ2;

6) 計(jì)算c=cosθ,s=sinθ及Givens旋轉(zhuǎn)矩陣;

7) 計(jì)算Givens旋轉(zhuǎn)后的拉普拉斯矩陣Lj+1=,若j＜J,則返回步驟1),繼續(xù)迭代;若j=J,則終止迭代,且輸出近似特征矩陣=S1S2…SJ,近似特征值=diagLj+1。

2.4 計(jì)算復(fù)雜度分析

2.4.1 截?cái)嘌趴杀人惴?/p>

尋找矩陣Lj中絕對(duì)值最大的元素是截?cái)嘌趴杀人惴ㄖ杏?jì)算復(fù)雜度最高的操作,其計(jì)算復(fù)雜度為O(‖Lj‖0),最壞情況下,該操作的計(jì)算復(fù)雜度為O(n2)。Givens旋轉(zhuǎn)前后的矩陣Lj與Lj+1僅有p、q兩行與p、q兩列的元素不相同,其余位置的元素都相同。若當(dāng)前迭代步驟中所選Givens旋轉(zhuǎn)坐標(biāo)p、q與前次選擇的不同,計(jì)算復(fù)雜度就能降到O(n)。實(shí)際計(jì)算過(guò)程中,絕大多數(shù)情況是2次選擇的坐標(biāo)不相同,因此截?cái)嘌趴杀人惴ǖ钠骄?jì)算復(fù)雜度為O(n2+nJ)。求得近似特征矩陣后,該矩陣與向量或矩陣相乘的計(jì)算復(fù)雜度為O(J)。

2.4.2 并行截?cái)嘌趴杀人惴?/p>

對(duì)矩陣Lk元素進(jìn)行排序是并行截?cái)嘌趴杀人惴ㄖ杏?jì)算復(fù)雜度最高的操作。在每步迭代中,最多需要對(duì)n(n-1)/2個(gè)元素進(jìn)行排序,該操作的計(jì)算復(fù)雜度為O(n2logn)。由于并行截?cái)嘌趴杀人惴ㄖ恍璧鶮=O(J/n)次,因此整體計(jì)算復(fù)雜度為O(nJlogn)。在求得近似特征矩陣后,運(yùn)用該矩陣與向量或矩陣相乘的計(jì)算復(fù)雜度為O(J)。并行截?cái)嘌趴杀人惴ㄖ忻總€(gè)旋轉(zhuǎn)因子Sk包含了n/2個(gè)Givens旋轉(zhuǎn),是一個(gè)并行計(jì)算過(guò)程。

為了使上述2種近似對(duì)角化算法的計(jì)算復(fù)雜度低于精確對(duì)角化,需要確保迭代次數(shù)J＜O(n2),通常迭代次數(shù)設(shè)為J=O(nlogn)。

3 仿真結(jié)果與分析

3.1 圖信號(hào)去噪

將截?cái)嗪筒⑿薪財(cái)嘌趴杀人惴ㄅc文獻(xiàn)[8]、[9]、[11]的算法在圖信號(hào)去噪上的性能進(jìn)行對(duì)比,所有仿真均在相同環(huán)境下進(jìn)行。用GSPBOX[18]構(gòu)建了Random sensor、Swiss roll、Community三種圖,圖上信號(hào)由圖拉普拉斯矩陣前10%的特征向量求和組成,圖2為節(jié)點(diǎn)數(shù)為128的3種圖信號(hào)。實(shí)驗(yàn)中,圖信號(hào)所添加的噪聲是均值為0、標(biāo)準(zhǔn)差為σ的加性高斯噪聲,圖濾波器組中的低通信道的閾值設(shè)為0,高通信道的閾值設(shè)為3σ。

圖2 3種不同拓?fù)浣Y(jié)構(gòu)的圖信號(hào)

表1～3為不同算法對(duì)含噪圖信號(hào)去噪后的信噪比,去噪結(jié)果是50次隨機(jī)實(shí)驗(yàn)結(jié)果的平均值。通過(guò)對(duì)比實(shí)驗(yàn)結(jié)果,可得如下結(jié)論:

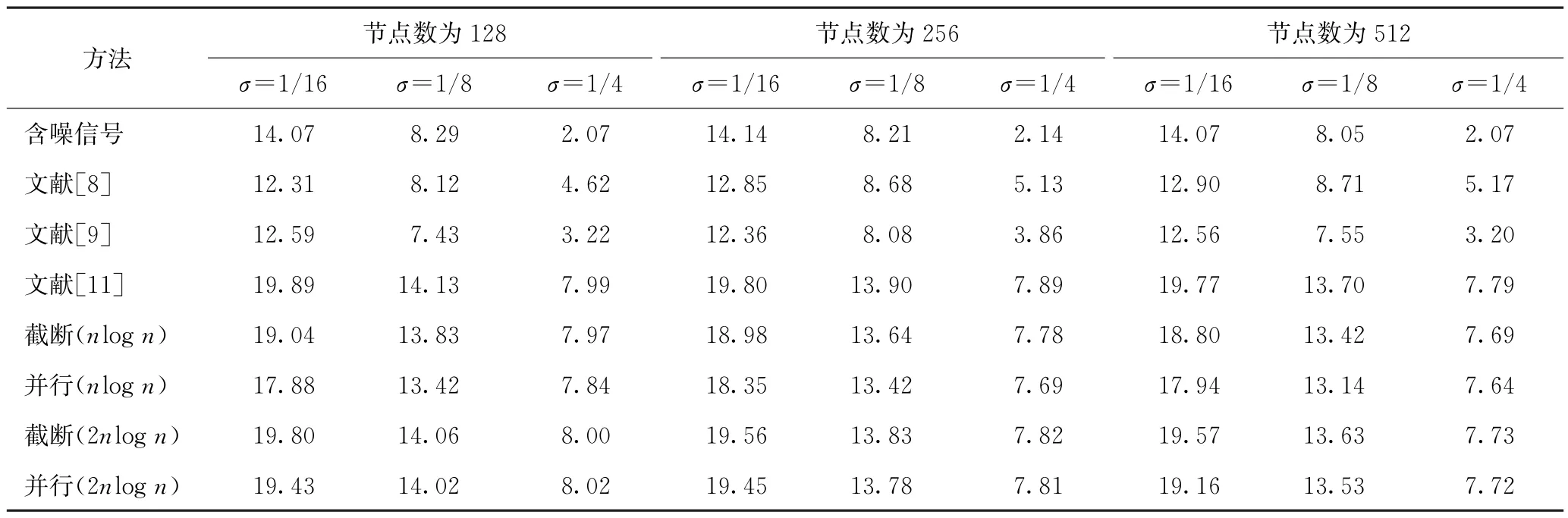
表1 sensor圖信號(hào)在不同算法下去噪后的信噪比 dB

表2 roll圖信號(hào)在不同算法下去噪后的信噪比 dB

表3 community圖信號(hào)在不同算法下去噪后的信噪比 dB

1)在Givens旋轉(zhuǎn)次數(shù)相同的情況下,截?cái)嘌趴杀人惴ǖ娜ピ胄Ч傮w上優(yōu)于并行截?cái)嘌趴杀人惴ā＿@是因?yàn)樵诿坎降^(guò)程中,截?cái)嘌趴杀人惴ǐ@得的解都是局部最優(yōu)解,而并行截?cái)嘌趴杀人惴ǐ@得的解并非局部最優(yōu)解,這導(dǎo)致了并行截?cái)嘌趴杀人惴ǖ氖諗克俣纫诮財(cái)嘌趴杀人惴ā?/p>

2)隨著Givens旋轉(zhuǎn)次數(shù)增加,截?cái)嘌趴杀人惴ㄅc并行截?cái)嘌趴杀人惴ǖ娜ピ胄Ч咏谖墨I(xiàn)[11],原因在于,隨著迭代次數(shù)的增加,2種算法求得的近似特征矩陣不斷趨近于精準(zhǔn)的特征矩陣。

3)在迭代次數(shù)較低時(shí),截?cái)嗪筒⑿薪財(cái)嘌趴杀人惴ㄈ〉玫娜ピ胄Ч獌?yōu)于文獻(xiàn)[8-9]。在頂點(diǎn)域采樣圖濾波器組中,圖信號(hào)與噪聲信號(hào)未得到有效分離,2種信號(hào)混雜程度較高,從采樣圖信號(hào)中難以有效濾除噪聲信號(hào)。而對(duì)于頻域采樣圖濾波器組而言,由于噪聲信息大多分布在高頻部分,圖信號(hào)與噪聲信號(hào)從頻域角度得到了有效分離。因此,頻域采樣圖濾波器組[11]的去噪效果要優(yōu)于頂點(diǎn)域采樣圖濾波器組[8-9],而改進(jìn)雅可比算法是對(duì)文獻(xiàn)[11]的一種近似,其去噪效果本質(zhì)上仍?xún)?yōu)于文獻(xiàn)[8-9]。

3.2 圖像去噪

在相同噪聲環(huán)境下對(duì)比不同算法對(duì)圖像的去噪性能。圖像可建模為一張圖,文獻(xiàn)[19]給出了圖像的8鄰域圖表示,其像素對(duì)應(yīng)于圖節(jié)點(diǎn),像素值則對(duì)應(yīng)于圖信號(hào),每個(gè)像素與其上下左右4個(gè)像素及2條對(duì)角線(xiàn)上的4個(gè)像素相連接,其邊的權(quán)重值由相鄰節(jié)點(diǎn)的像素值決定[20],如圖3所示。

實(shí)驗(yàn)選用了如圖4(a)所示的硬幣圖像,并以峰值信噪比(PSNR)和結(jié)構(gòu)相似性(SSIM)作為圖像去噪的性能評(píng)價(jià)指標(biāo)。圖4為不同算法去噪前后的圖像,表4、5分別為圖像去噪前后的峰值信噪比和結(jié)構(gòu)相似性。從圖4和表4、5可看出,與文獻(xiàn)[8-9]相比,改進(jìn)雅可比算法的去噪效果更好;與文獻(xiàn)[11]相比,去噪效果稍差,但隨著Givens旋轉(zhuǎn)次數(shù)的不斷增加,改進(jìn)雅可比算法的去噪效果不斷趨近于文獻(xiàn)[11]的去噪效果。另外,在低噪聲水平下,部分圖濾波器組未發(fā)揮作用,表現(xiàn)在去噪后信號(hào)信噪比低于含噪前,原因在于圖濾波器組濾掉的高頻部分不僅含有噪聲信息,還含有圖像的邊緣信息,去噪過(guò)程中原本的圖像信息遭到破壞,而真正的噪聲信息未得到有效處理。

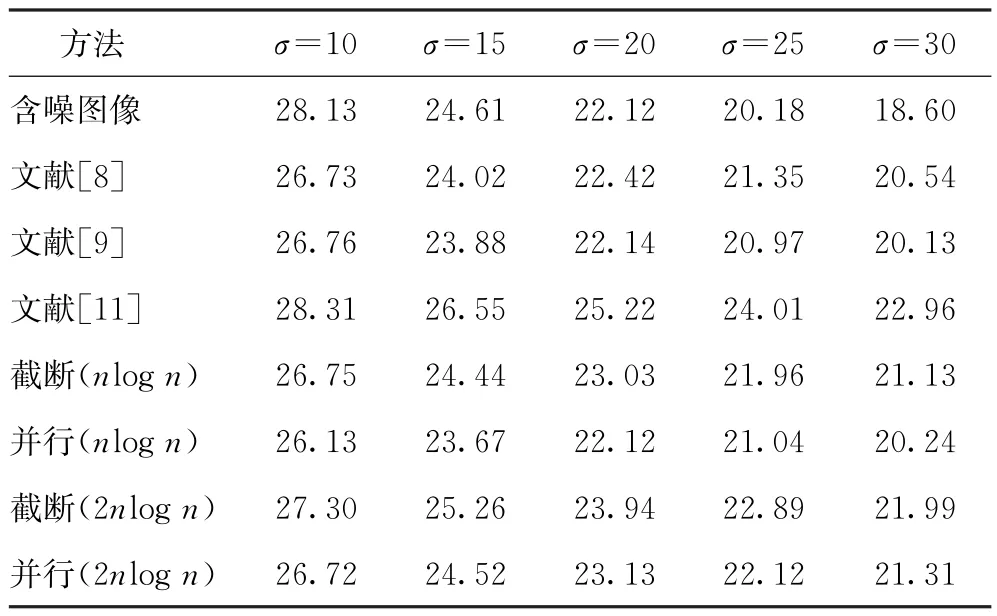
表4 圖像在不同算法下去噪前后的PSNR dB

圖4 硬幣圖像在不同算法下去噪前后的圖像

4 結(jié)束語(yǔ)

拉普拉斯矩陣的特征分解是頻域臨界采樣圖濾波器組中計(jì)算復(fù)雜度最高的運(yùn)算,當(dāng)圖的規(guī)模很大時(shí),計(jì)算代價(jià)過(guò)大。針對(duì)該問(wèn)題,使用2種改進(jìn)的雅可比算法近似求解頻域臨界采樣圖濾波器組中的特征矩陣,從而在保證完全重構(gòu)的前提下達(dá)到降低計(jì)算復(fù)雜度的目的。仿真實(shí)驗(yàn)結(jié)果表明,在迭代次數(shù)較低時(shí),截?cái)嗪筒⑿薪財(cái)嘌趴杀人惴ǖ娜ピ胄阅芤獌?yōu)于頂點(diǎn)域采樣圖濾波器組,且接近于傳統(tǒng)頻域臨界采樣圖濾波器組。