孔用楔形截面卡簧力學分析

黃澤康　宋東陽　呂海辰　趙晨　屠義承　譚穎穎

摘 要：卡簧是機械部件中常用的軸向緊固件，對軸承、齒輪等零部件軸向運動提供阻止作用，一方面可以保證機器設備工作可靠性并延長各零部件的工作壽命，同時其可以減少零部件間工作噪音的產生。本文基于材料力學方法推導出了孔用偏心卡簧受力與變形的理論計算式子，利用有限元仿真軟件ANSYS-Workbench對卡簧工作狀態下的徑向力、軸向力進行了分析。結果表明，數值模擬分析推導結果與建模分析結果基本一致，為楔形截面偏心卡簧的設計與優化提供了理論參考。

關鍵詞：孔用卡簧 楔形截面 彈性變形 有限元分析

1 引言

零件軸向定位常用的方法有軸肩、套筒、圓螺母、擋圈、圓錐形軸頭等，卡簧是擋圈中的一種，是常用的軸向定位機械零件。卡簧根據使用場景可分為軸用卡簧與孔用卡簧，或稱為外卡簧與內卡簧，按照其內外圈是否同心可分為同心型卡簧與偏心型卡簧[1]；卡簧截面也有多種，常見的有矩形截面與楔形截面。卡簧偏心距、截面形狀尺寸等對卡簧的性能都有極大影響，對于標準卡簧不能滿足的工況，必要情況下可對卡簧參數（外徑、內徑、偏心距厚度等）進行調整以滿足特定工況需求。本文對孔用偏心楔形卡簧進行力學分析，推導出卡簧受載時開口端產生彈性變形與載荷的關系，并根據有限元分析，進一步驗證卡簧計算的理論模型。

2 卡簧尺寸設計理論模型推導

2.1 中性面位置推導

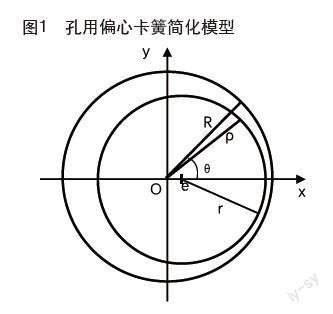
孔用偏心卡簧簡化模型如圖1所示，由于截面無法做到任何角度都同時與內外圓心重合，為方便計算，取截面與外圓圓心重合，外圓圓心為坐標系原點；楔形截面形狀如圖2所示，楔形截面的β角為定值，故截面的梯形部分形狀尺寸固定；由于內外圈偏心，所以不同的角度θ對應的截面面積不同。

內圓的直角坐標方程為：

（x-e）2+y2=r2? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （1-1）

將內圓的直角坐標方程（式1-1）轉化為極坐標方程：

ρ=? ? （1-2）

如圖2，取ｙ為自變量，ｘ為因變量：

x=b? ? y∈（ρ，tan（-β）（b-a）+R）? （1-3）

x=+a y∈（tan（-β）（b-a）+R，R）? （1-4）

截面面積Ａ：

A=∫ρtan（-β）（b-a）+Rbdy+∫Rtan（-β）（b-a）+R+ady? ?（1-5）

截面對ｘ軸的靜矩Sx：

Sx=ydA=ydxdy? ? ? ? ? ? ? ? ? ? ? ? （1-6）

矩形部分對ｘ軸的靜矩Sx1：

Sx1=yxdy= yb dy

（1-7）

梯形部分對ｘ軸的靜矩Sx2：

Sx2=y×dy? ?（1-8）

截面對ｘ軸的靜矩Sx：

Sx=Sx1+Sx2? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （1-9）

截面形心到ｘ軸的距離：

=? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（1-10）

是關于角度θ的關系式，可通過繪圖軟件繪制參數曲線得到與θ的圖像，如圖3所示，繪制出的圖像與圓形高度相似。

2.2 截面慣性矩推導

以上求得圖2截面形心到ｘ軸的距離為

在圖2中，取y=時為y軸原點，如圖4所示，此時有：

x=+a? y∈[tan（-β）（b-a）+（R-），R-]

（1-11）

在圖4中，以y=0為截面中性軸，截面對ｘ軸的截面慣性矩Iｘ：

Ix=y2da

矩形部分對ｘ軸的截面慣性矩Iｘ1：

Ix1=xy2dy=

by2dy? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （1-12）

梯形部分對ｘ軸的截面慣性矩Iｘ2：

Ix2=xy2dy=

（+a）×y2dy? ? ? ? ? ? ? ? ? ? ? ? （1-13）

截面對ｘ軸的截面慣性矩Iｘ：

Ix（θ）=Ix1+Ix2? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（1-14）

2.3 徑向受載與變形分析推導

在生產線裝配過程中，孔用卡簧常用裝配方法為壓裝，即通過套筒進行安裝，安裝過程中對孔用卡簧造成變形的載荷為徑向均布載荷；裝配后，對擋圈造成彈性變形的載荷主要為徑向載荷，如圖4所示。

由于卡簧具有對稱特性，取卡簧的一半作為研究對象[2]，卡簧外圈承受均布載荷q（均布載荷q單位為N/mm，在值上等于截面上的壓力與受壓寬度的乘積，若整個外圈受壓，外圈厚度為a，q=p×a，p為壓力，單位為MPa），在均布載荷作用下，擋圈開口處發生沿y軸的相對位移為δ1，沿x軸的相對位移為δ2，在截面處有彎矩Mθ、剪力Qθ、軸力Fθ。

由截面法可得截面處彎矩與軸力表達式：

Mθ=qR2sin（θ-φ）dφ=qR2[1-cos（θ-）]

（1-15）

Fθ=qRsin（θ-φ）dφ=qR[1-cos（θ-）]

（1-16）

截面處的正應力由軸力與彎矩作用下產生，故截面處正應力σθ為：

σθ=+? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（1-17）

式（1-17）中：W為抗彎截面系數，

W=

計算卡簧開口處位移δ1、δ2可利用材料力學計算彎曲變形時的莫爾定理進行計算，在開口端施加垂直于x軸的單位力F1，垂直于y軸的單位力F2如圖7所示，所對應的位移即為沿單位力方向的位移，由單位力在各截面產生的對應彎矩為：

M1=R[1-cos（θ-）]? ? ? ? ? ? ? ? ? ? ?（1-18）

M2=R（sinθ-sin）? ? ? ? ? ? ? ? ? ? ? （1-19）

在卡簧正常工作時，變形由彎矩、剪力和軸力共同作用下產生，但軸力和剪力對變形的影響很小，為簡化計算可以忽略不計，故只考慮彎矩的影響[3]。

δ1=? ? ? ? ? ? ? ? ? ? ?（1-20）

δ2=? ? ? ? ? ? ? ? ? ? ?（1-21）

δ=? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（1-22）

式中：

E為材料彈性模量；

Ix為截面慣性矩，是關于θ的函數關系式；

M1為在單位力F1作用下對應的彎矩，是關于θ的函數關系式；

M2為在單位力F2作用下對應的彎矩，是關于θ的函數關系式；

Mθ為在均布載荷q作用下對應的彎矩，是關于θ的函數關系式。

將式（1-20）、（1-21）積分后可得到卡簧開口端沿y、x方向的位移δ1、δ2，將δ1、δ2合成得到卡簧開口端合位移δ與q的關系式：

δ=kq? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （1-23）

式（1-23）中，k為常數，由式（1-22）化簡后得出，本文是利用MATLAB進行計算得到k值，當q=1N/mm時，在數值上有δ=k。

式（1-23）中的均布載荷q與卡簧自身徑向彈力F彈的關系為：

q=? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（1-24）

2.4 軸向力推導

孔用楔形截面卡簧在工作中受力如圖8所示，當卡簧安裝后，卡簧會受到擠壓產生彈性變形，從而自身產生彈力F彈，同時由于作用力與反作用力還受到對手件對楔形面的正壓力N和底面的軸向力F軸，自身彈力可為裝配體提供一定的預緊力。

當設備工作運行時，卡簧會受到的載荷越來越大，導致卡簧受力開始運動變形時，有：Fr=F彈+F1+F2cosβ? ? ? ? ? ? ? ? ? ? ?（1-25）

式（1-25）中：Fr=Fttanβ=F軸tanβ，F1、F2分別為底面和楔形面受到的摩擦力

F1=F軸1，F2=N2=2=2

故當卡簧受力開始運動變形時，有：

F軸=? ? ? ? ? ? ? ? ? ? （1-26）

將式（1-24）代入式（1-26），有：

F軸=? ? ? ? ? ? ? ? （1-27）

在卡簧未產生自鎖的情況下，即1=0，2=0，此時的F軸為卡簧變形產生的軸向預緊力。

3 模擬仿真分析與結果對比分析

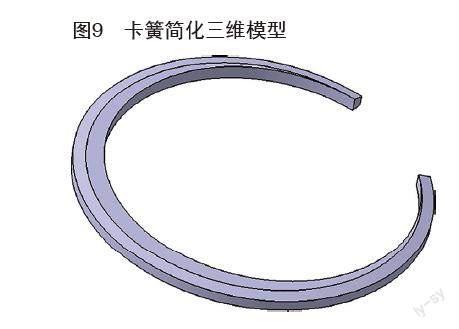
本文使用的是ANSYS-Workbench軟件進行仿真分析，有限元分析主要有三個步驟，前處理、求解和后處理，其中前處理（如圖9所示）包括幾何模型的導入、材料屬性定義、網格劃分、負載和邊界條件定義。

（1）導入幾何模型

在CATIA中繪制好三維模型后保存成ANSYS能夠識別的文件格式，在ANSYS的靜態結構（Static Structure）導入幾何模型。由于導入的幾何模型表面會產生一些線條，對網格劃分會造成影響，所以在導入幾何模型后在Design Modeler模塊中對幾何模型表面進行處理，將模型表面上的不必要的線條進行合并處理，對需要進行表面劃分的地方進行分割。

（2）定義材料屬性

導入幾何模型之后，在工程數據（Engineering Data）欄中定義好材料參數，以備后續調用，本文分析的卡簧材料為C75S，材料參數如表1所示。卡簧賦予C75S材料。

（3）劃分網格

在有限元建模中，網格劃分是一個非常重要的步驟，它必須同時兼顧分析和計算的準確性，又要考慮計算時間成本的問題，在對復雜模型進行網格劃分時，網格劃分的工作量比較大。在劃分網格時，需要參考的四個基本原則：單元類型、網格數量、網格疏密、網格質量。

3.1 徑向受載模擬仿真及理論分析結果對比

本文使用CATIA對GB/T 893-2017中的多種規格卡簧進行參數化建模，并使用ANSYS-Workbench對這多種規格卡簧進行有限元分析，以驗證理論方法的正確性。

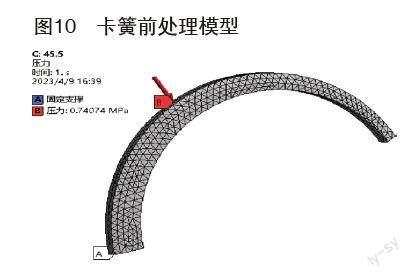
表2為從GB/T 893-2017中隨機選擇的14種規格卡簧的參數，使用公稱規格為42mm的卡簧建立簡化三維模型如圖10所示，圖11為前處理模型，所使用的網格類型為四面體網格，約束類型為固定約束A，施加在截面處，載荷類型為圓周方向的均布載荷B，大小為1N/mm，在ANSYS-Workbench中施加壓力為0.74074MPa。圖12為有限元分析求解總變形結果云圖，圖13為有限元分析求解等效應力結果云圖，表3為有限元分析結果與理論計算結果，圖14、圖15為理論計算結果與有限元計算結果曲線圖，結果表明理論計算的變形結果、應力結果與有限元計算變形結果、應力結果基本一致，其中由于施加的均布載荷q=1N/mm，理論計算變形結果在值上與式1-23中的k相等。

3.2 軸向力模擬仿真及理論分析結果對比

式1-27為軸向力F軸與變形δ的關系，圖16為用ANSYS-Workbench對卡簧軸向受載創建的有限元模型，對模型劃分好網格之后進行邊界條件的施加，底座施加固定約束，卡簧和底座之間定義為無摩擦接觸，卡簧和壓塊之間定義為無摩擦接觸，在壓塊上表面施加軸向0.4mm位移，由表3可知對于公稱規格為42mm的卡簧的k=0.645453，表4為公稱規格為42mm的卡簧的相同變形時的有限元與理論計算軸向力結果，圖18為總變形與軸向力對應關系曲線圖，結果表明，有限元仿真分析與理論計算的結果偏差不大。

4 結論

本文建立了孔用楔形截面卡簧的數學模型，通過材料力學方法推導出孔用偏心卡簧的受力與變形的關系式，得出徑向受載與變形的關系，并得出卡簧徑向載荷與變形的比例系數k，進而得到變形與軸向力的關系式。

通過有限元分析法與理論計算對多種規格卡簧進行對比，結果表明在相同的徑向均布載荷條件下，理論計算變形結果的偏差在±5%之內，在相同變形條件下，理論計算軸向力結果的偏差在±10%之內，可為卡簧提供軸向力設計分析提供參考[4]。

基于以上方法論，可結合卡簧使用工況及外界受力對卡簧設計參數進行適當調整，以滿足相關工況需求，為卡簧及其對手件設計提供了行之有效的方法論支持及實踐指導。

參考文獻：

[1]靳倩倩.某手動變速器中五齒軸用彈性擋圈斷裂分析[J].汽車制造業，2020（13）：29-31.

[2]劉洋，楊晉，張劍平，徐玄.開口圓環過盈聯接力學分析[J].航空精密制造技術，2014，50（04）：55-57.

[3]張保生.勻彈力變截面開口圓環的彈力集度及強度計算[J].機械科學與技術，1994（03）：95-97.

[4]郝忠獻，李根生，高向前，錢杰，郭瑞昌.滑閥卡簧定位力有限元分析與優化[J].石油礦場機械，2010，39（01）：50-53.