基于不等分剪切模型的ZM5鎂合金本構參數的逆向辨識

王伏林 肖 強 來書寧 唐能藝

湖南大學機械與運載工程學院,長沙,410013

0 引言

ZM5鎂合金作為一種輕質鎂鋁鋅合金,具有優良的鑄造性能及較好的力學性能,被廣泛應用于航空和汽車領域,如用于制造飛機輪轂、航天器殼體和轎車齒輪傳動變速箱體等[1-3]。為滿足精密鎂合金零件的加工需求,需要對鎂合金的高精密切削加工技術開展進一步研究。但ZM5鎂合金的燃點較低,而切削加工中99%的切削變形和摩擦所消耗的功會轉化為熱能,這導致ZM5鎂合金在切削過程中存在切屑自燃的安全隱患[4]。利用有限元仿真技術來模擬切削加工過程中的應力場及溫度場變化,可為ZM5鎂合金的安全切削加工提供一種預判手段,而精確反映材料力學性能變化的本構模型是保證ZM5鎂合金切削仿真可靠性的基礎。

目前,ZM5鎂合金動態力學性能參數的缺失限制了其在高速切削加工領域的應用。在ZM5鎂合金切削過程中,伴隨著高溫和高應變率,工件會發生較大的剪切變形,本構模型是描述此過程的關鍵。在常用的材料本構模型中,Johnson-Cook本構模型(J-C本構模型)因綜合考慮了材料應變硬化、應變率強化和溫度軟化效應的影響,模型中的參數容易通過實驗獲取,故被廣泛用于描述金屬材料切削加工過程的力學行為[5]。J-C本構參數確定方法主要有三種:霍普金森動態實驗法(SHPB)、有限元法和切削試驗法。相比于復雜繁瑣的有限元法和SHPB實驗法,采用不等分剪切區理論與尋優算法結合的切削試驗法,既簡化了實驗操作,又可較好地描述材料加工過程中的熱軟化效應和加工硬化行為,吸引了不少學者進行研究。李秀儒等[6]基于不等分剪切區模型,結合準靜態壓縮試驗和正交切削試驗,利用粒子群算法逆向識別了316H不銹鋼的J-C本構參數,并通過仿真驗證了參數的準確性。盛鷹等[7]采用一種自適應多層復形遺傳算法,對Ti-6A-4V鈦合金本構參數進行求解,將數值模擬結果與已有試驗數據進行比較,驗證了方法的可行性。潘鵬飛等[8]將Oxley切削理論和正交切削試驗相結合,通過遺傳算法對熔石英高溫玻璃的J-C本構參數進行逆向求解,并通過試驗驗證了逆向識別方法的可行性和本構模型的準確性。陳冰等[9]基于不等分剪切區理論,利用遺傳算法逆向求解高溫合金的J-C本構參數,并通過仿真驗證了模型的準確性。

綜上,目前針對ZM5鎂合金材料本構參數的求解研究較少,并且在眾多研究中,大多采用標準遺傳算法一次對五個參數進行求解。雖然該方法可以一次識別較多參數,但是需要預先知道參數的大致范圍,否則會降低求解精度,且辨識時間較長。為解決ZM5鎂合金動態力學性能參數缺失的問題,提高反求參數的精度,本文提出一種基于不等分剪切區理論的ZM5鎂合金J-C本構參數逆向識別方法。

1 J-C參數求解理論模型構建

1.1 剪切區理論模型分析

金屬切削加工過程中,熱力耦合作用使工件材料發生塑性變形,在第一變形區會產生較大的剪切應變和應變率。以不等分剪切模型[10]為主,結合Merchant單一剪切模型[11]和Oxley平行剪切帶理論[12],對切削過程中剪切區的應力、應變、應變率以及溫度進行理論模型構建,可為后續逆向辨識ZM5鎂合金J-C本構參數提供理論基礎。圖1為不等分剪切區模型的分析示意圖。

剪切角φ反映了切削過程中的變形大小,由Merchant最小功率理論[11]可得剪切角計算式如下:

(1)

式中,γ0為刀具前角;β為摩擦角。

由圖1的幾何關系可知摩擦角

(2)

(3)

式中,Fm、Fp分別為剪切區前刀面摩擦力和正壓力:Fc、Ff分別為主切削力和進給抗力。

同時,剪切面AB處的剪切力Fs和法向力Fn也可由Fc、Ff表示:

(4)

不等分剪切區模型假定主剪切面AB上的剪切應力τAB均勻分布,則有

(5)

式中,As為主剪切面AB的面積;W為切削寬度(相當于切削加工過程中的背吃刀量);tc為切削厚度。

由式(4)、式(5)可得

(6)

(7)

d用于描述剪切變形區中切向速度的不一致性,與材料屬性和切削狀態有關,d取4時的應變率分布更加符合實際[13]。文獻[13]給出了剪切區厚度h的表達式:

(8)

如圖1所示,在B點處,以B點為圓心、BA方向為x軸正向構建oxy笛卡兒坐標系。在剪切區對速度進行分解,沿著剪切面AB方向的速度分量為vx,垂直于剪切面AB方向的速度分量為vy。由文獻[14]可知,vy在整個主剪切帶中恒定,vx的大小與剪切區厚度變化有關,切削過程中剪切速度關系可由下式表示:

(9)

其中,v為切削速度。考慮vx的上下邊界條件,在式(7)中對y求積分可得剪切區切向速度場

vx=

(10)

將主剪切面的切向速度vx|y=0=0代入式(10)可得主剪切面AB的等效應變率

(11)

和剪切區不等分系數

(12)

(13)

將式(13)中y從-ah到0積分,可以得到主剪切面AB處的等效應變

(14)

為了簡化模型,通常將剪切區域視為處于絕熱狀態,忽略熱傳遞現象。根據BOOTHROYD等[15]提出的切削溫度模型,可得主剪切面AB處的平均溫度

tAB=tw+ηΔtAB

(15)

(16)

式中,tw為環境溫度;η為變形能轉化為熱量的比例(通常取0.9);ΔtAB為剪切平面AB的溫升;ρ為工件材料的密度;c為工件材料的比熱容;vs為剪切速度,有vs=vcosγ0/cos(φ-γ0);λ為第一變形區產生的熱量導入工件的比例。

λ值可表示為

(17)

RT=ρcvtc/κ

(18)

式中,RT為量綱一常數;κ為材料熱導率。

1.2 求解模型構建

J-C本構模型形式簡單,并且可以很好地描述切削過程中力學行為變化,在切削加工中經常被使用,其表達式為

(19)

(20)

式中,N為切削試驗總次數(本文N=16);i為切削試驗序號。

2 試驗參數獲取

2.1 準靜態拉伸試驗

準靜態拉伸試驗樣件為光桿試件,試件尺寸如圖2所示。試驗設備為INSTRON-8801萬能試驗機。試驗溫度為室溫20 ℃,拉伸速率為2 mm/s,參考應變率為0.01 s-1。將實驗獲得的數據進行處理,得到真實應力-應變曲線(圖3)。

圖2 準靜態拉伸試驗試件Fig.2 Quasi-static tensile test piece

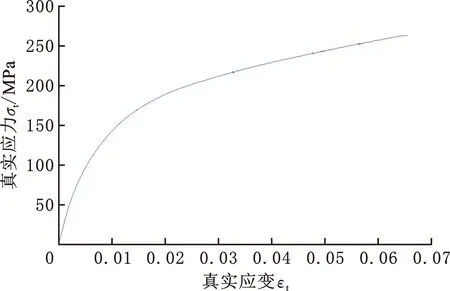
圖3 準靜態下ZM5鎂合金的真實應力-應變曲線Fig.3 Quasi-static true stress-strain curve of ZM5 magnesium alloy

由圖3可知,在ZM5鎂合金準靜態拉伸的過程中,沒有出現明顯的屈服階段,根據國際通用規定取0.2%塑性變形時的應力作為ZM5鎂合金的屈服強度,可得ZM5準靜態條件下的屈服強度A=130 MPa。J-C本構模型考慮了應變、應變率、溫度對應力的影響,當C=0且t=t0時,試驗處于準靜態狀態下,式(19)可簡化為

(21)

為了確定B、n,對式(21)進行變形,得到

(22)

利用MATLAB軟件對B、n進行擬合求解,得到其在置信區間為95%下的數值為B=380.5 MPa,n=0.6256。

2.2 正交切削試驗

(a)正交切削現場試驗裝置圖

(b)試驗測量原理圖圖4 正交切削試驗Fig.4 Orthogonal cutting experiment

開展ZM5鎂合金正交切削試驗,獲得不同切削條件下鎂合金的切削力數據。圖4a為ZM5鎂合金正交切削現場試驗裝置圖,圖4b為試驗測量原理圖。試驗采用CM6140普通車床,試驗工件為φ60 mm×300 mm的ZM5鎂合金棒料,切削刀具為YT15類硬質合金外圓車刀,刀具前角15°,后角8°,刃傾角0°,采用干切削,主切削力和進給抗力采用DCL-03A三向測力儀進行測量,采用K型熱電偶絲對切削過程中的刀尖溫度進行測量。為使切削過程盡可能滿足直角切削條件,保證鎂合金切削安全性,盡量選取較大的背吃刀量ap,參照文獻[16]選取切削參數,確定背吃刀量ap為1.5 mm,其余試驗參數以及測量結果如表1所示。

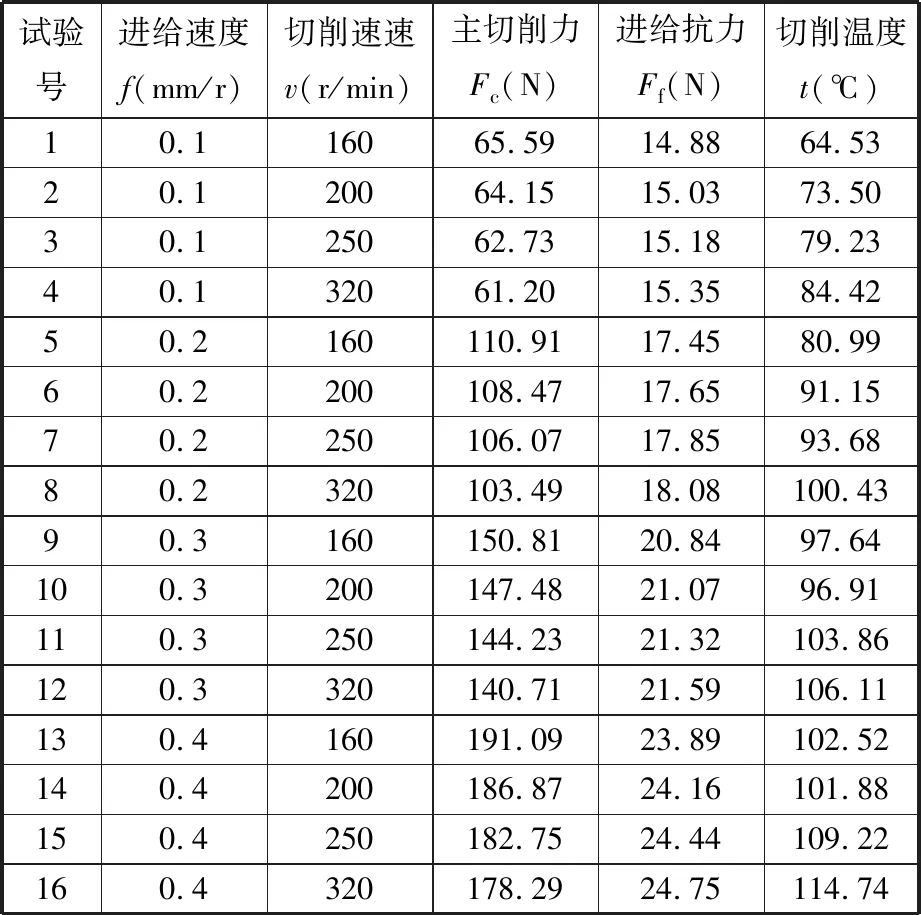
表1 ZM5鎂合金正交切削試驗參數及測量結果

3 基于混合粒子群算法的J-C本構參數反求

目前對材料J-C本構參數的反求一般采用基本遺傳算法或標準粒子群算法,這兩種算法形式簡單,但均存在一定不足。遺傳算法能夠保持種群的多樣性但收斂運算速度慢,而標準粒子群算法雖然收斂速度快但容易陷入局部最優解,識別精度不高。因此,為了獲得更精確的ZM5鎂合金本構參數,本文對標準粒子群算法進行改進:對標準粒子群算法的動態慣性權值進行調整,引入遺傳算法中的交叉和變異操作,通過粒子同個體極值和群體極值的交叉以及粒子自身變異的方式搜索最優解,提高搜索準確性與收斂速度。

3.1 慣性權重系數w的動態調整

慣性權重系數w展現的是粒子保持先前運動速度的能力,w值越大則全局搜索能力越強,局部搜索能力越弱。為了更好地平衡粒子的全局搜索和局部搜索能力,需要針對不同時期的搜索情況對w值進行動態調整。由文獻[17]可知,凸函數遞減慣性權值在迭代前期,w變化較慢,取值較大,能夠維持算法的全局搜索能力;在迭代后期w變化較快,可極大地提高算法的局部搜索能力,更有利于獲得較好的全局最優解。因此本文選用凸函數慣性權值,其表達式如下:

(23)

式中,k為當前迭代次數;Tmax為允許的最大迭代次數;wmax為最大慣性權值;wmin為最小慣性權值,一般來說,慣性權值wmax=0.9、wmin=0.4時算法性能最好。

3.2 遺傳算法改進粒子群算法

將遺傳算法的交叉和變異策略應用到粒子群算法中,通過粒子同個體極值和群體極值的交叉以及粒子自身的變異來搜索最優解,與傳統的粒子群算法相比,提高了粒子種群的多樣性和全局搜索能力。在種群每次進化過程中,利用交叉概率Pc篩選一定數量的粒子放入交叉池中,池內的粒子隨機兩兩交叉[18],其速度和位置的變化規則為

(24)

(25)

采用高斯變異的方式[19],根據變異概率Pm隨機選取部分粒子進行變異,用符合均值為μ、方差為σ2的正態分布的一個隨機數Q來替換原來的基因值。在具體實現高斯變異時,符合正態分布的隨機數Q可通過下式,利用一些符合[0,1]均勻分布的隨機數Rg(g=1,2,…,12)來產生:

(26)

(27)

3.3 本構參數C、m的逆向求解

在MATLAB 2018a平臺上對ZM5鎂合金的J-C本構方程進行反求,將準靜態拉伸試驗和切削試驗獲得的參數作為輸入變量代入剪切區理論模型中,求得剪切區的等效剪切應變率、等效應變、等效應力以及剪切區溫度。采用混合粒子群算法對J-C本構參數的C和m進行迭代求解,直至滿足目標函數收斂,具體流程如圖5所示。

圖5 本構參數C和m逆向識別流程Fig.5 Reverse identification process of constitutive parameters C and m

參照文獻[20]確定參數C和m的大致范圍為:-1.5≤C≤1.5,-1.5≤m≤1.5。改進混合粒子群算法的種群數為20,迭代次數為200,交叉概率Pc設為0.5,變異概率Pm設為0.05,學習因子設為1.5,慣性權重采用凸函數遞減,初始慣性權重為0.9,終止慣性權重為0.4。J-C本構參數搜索的適應度值隨迭代次數的變化如圖6所示。由圖6可知,在種群迭代至96代左右時,適應度值趨于穩定并收斂,得到:C=0.0972,m=1.2315。結合準靜態拉伸試驗獲得A、B、n,最終得到ZM5鎂合金的J-C本構方程表達式為

圖6 適應度值隨迭代次數的變化趨勢Fig.6 The trend of fitness value with the number of iterations

(28)

4 模型驗證與討論

為了驗證采用混合粒子群算法所求得的J-C本構模型的準確性,將所獲得的ZM5鎂合金J-C本構方程輸入AdvantEdge FEM軟件中進行二維切削仿真,并將其得到的仿真值與軟件自帶鎂合金材料模型和試驗測量值進行對比分析。其中仿真所用的切削條件與試驗相同,仿真中涉及的ZM5鎂合金相關物理參數如表2所示。切削二維模型如圖7所示。刀具和工件的網格劃分采用自適應網格,環境溫度設為20 ℃。驗證數據選用表1中實驗序號為奇數的數據。

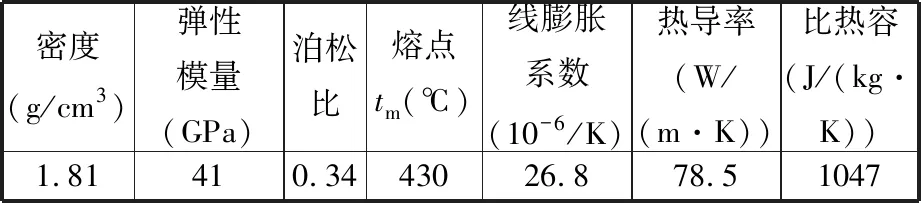
表2 ZM5鎂合金物理性能參數

圖7 ZM5鎂合金二維切削仿真模型Fig.7 Two-dimensional cutting simulation model of ZM5 magnesium alloy

圖8所示為AdvantEdge軟件中自帶本構參數與基于逆向識別本構參數的切削力和切削溫度仿真結果與試驗結果的對比。表3所示為兩種本構模型獲得的仿真值與試驗值的誤差結果對比。

(a)主切削力對比

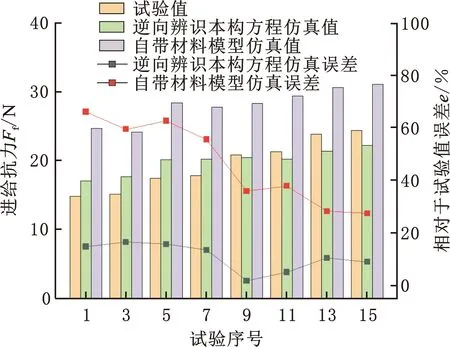
(b)進給抗力對比

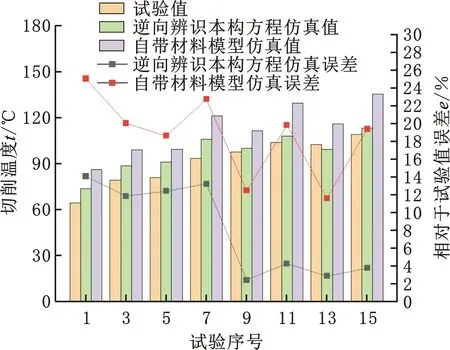
(c)切削溫度對比圖8 兩種本構參數仿真值與試驗值的對比Fig.8 Comparison of the simulation values and test values of the two constitutive parameters

由圖8和表3可知,相較于軟件自帶材料參數所獲得的仿真結果,基于逆向辨識本構方程所獲得的仿真結果更加精確,所獲得的主切削力、進給抗力和切削溫度與試驗值的平均誤差分別為7.01%、10.84%和8.11%,均在誤差允許范圍(15%)以內。軟件自帶材料模型仿真得到的進給抗力和切削溫度與試驗值相差比較大,尤其是進給抗力,與試驗值誤差為46.72%,已遠遠超過誤差允許范圍,而基于逆向辨識本構方程所獲得進給抗力與試驗值更加接近。綜上,基于逆向辨識本構方程獲得的主切削力、進給抗力和切削溫度均比軟件自帶材料模型獲得的結果更為準確,且相對于試驗值的誤差均在15%以內,充分說明基于逆向辨識獲得的本構參數具有較高的準確性,證明了本文所提出逆向求解方法的可行性。

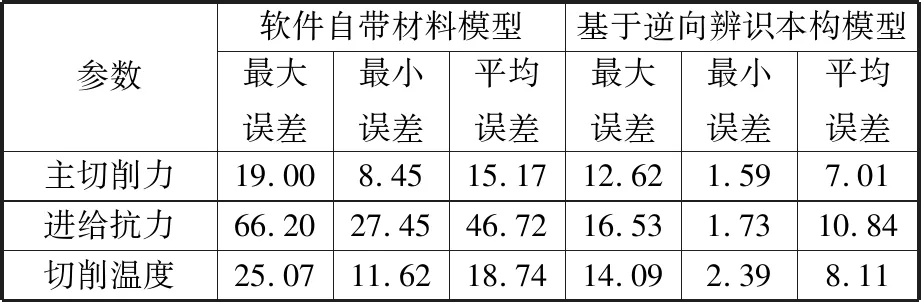
表3 兩種本構參數仿真值與試驗值的誤差

5 結論

(1)本文提出一種基于不等分剪切區理論的ZM5鎂合金J-C本構參數逆向識別方法,解決了ZM5鎂合金動態力學性能參數缺失和傳統霍普金森實驗求解結果與實際切削過程相差較大的問題。

(2)本文將凸函數慣性權值引入到標準粒子群算法中,并與遺傳算法交叉變異策略相結合,采用混合粒子群算法求解得到ZM5鎂合金的J-C本構參數,提高了參數反求的精度和求解速度。

(3)建立基于所求本構參數的二維仿真模型,通過仿真結果與試驗值進行對比分析,結果表明:基于辨識所求本構方程的主切削力、進給抗力和切削溫度的仿真結果與試驗值平均誤差較小,分別為7.01%、10.84%和8.11%,證明了本文本構方程的準確性。