大管徑管道冰漿流動阻力特性實驗研究*

唐道軻 付 林 楊 波 李永紅 李建剛

(1.清華大學(xué),北京;2.北京航空航天大學(xué),北京;3.太原市熱力集團(tuán)有限公司,太原)

0 引言

作為冷凍法的一種,動態(tài)制冰在水處理領(lǐng)域已有一定的研究和應(yīng)用,包括廢水再生[1]和海水淡化[2]。動態(tài)制冰法通常利用過冷解除、真空閃蒸等技術(shù),直接在流動的水中生成細(xì)小的冰晶顆粒,形成流態(tài)的冰水混合物,即冰漿。水在結(jié)冰過程中,鹽分和雜質(zhì)會被自動排除在冰晶之外,再經(jīng)過洗滌、分離、融化等一系列過程,最后就能得到較為純凈的淡水。而在此之外,冰漿在區(qū)域供冷領(lǐng)域有著更廣闊的應(yīng)用前景[3-5]。一方面蘊(yùn)含著可觀的潛熱,另一方面還具備流動性。冰漿是非常理想的供冷介質(zhì),尤其是制備過程中可以利用峰谷電價差[6]或跨季節(jié)廢熱。冰漿供冷是實現(xiàn)低碳、高效供冷的有效途經(jīng)之一。

冰漿應(yīng)用不可避免要涉及輸送問題。冰漿屬于固液兩相流,當(dāng)含冰率超過一定值時,冰漿會表現(xiàn)出非牛頓流體特征,即剪切應(yīng)力與速度梯度不再成正比,其阻力特性相較于單相流更為復(fù)雜。目前,主要有4種流變模型用來描述冰漿的非牛頓流體特征,包括Bingham、Casson、Power Law、Herschele-Bulkley等[7]。有研究表明,Herschele-Bulkley模型與實驗結(jié)果最為接近,但最大偏差也會達(dá)到30%以上[8]。

劉永紅等人針對管徑為8.83 mm的光滑銅管開展實驗研究,發(fā)現(xiàn)在低流速下冰漿阻力比純水大,而在高流速下則與含冰率密切相關(guān),含冰率在2%～30%以下時冰漿阻力反而比純水小,這可能與冰漿的再層流化有關(guān),冰晶的存在會抑制層流向湍流的轉(zhuǎn)化[9]。王繼紅等人采用Power Law流變模型來描述冰漿層流流動,即壁面剪切應(yīng)力與剪切速度滿足指數(shù)關(guān)系,實驗發(fā)現(xiàn),隨著含冰率(10%～25%)和管徑(DN25和DN40)增大,流變系數(shù)K增大,而流變指數(shù)n則減小且始終大于1[10]。Illan等人發(fā)現(xiàn)在低雷諾數(shù)下含冰率越大則阻力越大,且顯著大于純水,而在高雷諾數(shù)下冰漿的阻力系數(shù)曲線基本與單相的Blasius線重合,而與含冰率無關(guān),實驗中的管徑在16.1～35.7 mm之間,含冰率在5%～26%之間[11-12]。Bordet等人利用可視化手段對冰漿流動型態(tài)進(jìn)行了歸類,實驗工況覆蓋了從純水到18.4%含冰率,也發(fā)現(xiàn)了與文獻(xiàn)[11-12]相似的阻力特性變化規(guī)律[13]。需要指出的是,以上研究中,前3個采用的都是質(zhì)量含冰率,Bordet等人采用的則是體積含冰率,而本研究采用的也是體積含冰率。

從目前檢索到的文獻(xiàn)來看,現(xiàn)有研究或受限于實驗條件,或由于面向的應(yīng)用規(guī)模較小,冰漿輸送管道多是在管徑50 mm以下,而且更多是在10～30 mm,流動多屬層流或低雷諾數(shù)湍流,對于更大管徑、更高雷諾數(shù)的研究和應(yīng)用則很少看到,而未來大規(guī)模的水處理和區(qū)域供冷應(yīng)用必然需要更大的冰漿輸送能力、更大的輸送管徑。已有研究指出,管徑對冰漿流動特性影響顯著,在小管徑下,近壁面升力和湍流擴(kuò)散力的影響效應(yīng)能覆蓋較大的管高范圍,而大管徑下這些動量傳遞機(jī)制的影響范圍有限,更容易出現(xiàn)非均質(zhì)流[14-15]。因此,有必要針對大管徑輸送開展冰漿流動阻力特性研究,填補(bǔ)現(xiàn)有研究的空白。

1 冰漿阻力特性實驗臺

本文針對DN50(內(nèi)徑52 mm)和DN80(內(nèi)徑78 mm)2種大管徑的無縫鋼管開展冰漿流動阻力特性實驗研究。冰漿阻力實驗臺如圖1所示,實驗所用冰漿由1臺吸收式真空制冰機(jī)提供,存放在1個帶攪拌器的罐子中,通過調(diào)節(jié)攪拌器轉(zhuǎn)速可以改變輸送出去的冰漿含冰率,冰漿由漿體泵抽出送入測試段,最后回到攪拌罐。測試段包含DN50和DN80 2段并聯(lián)的3 m長直管路,可通過閥門進(jìn)行切換,DN50和DN80測試段末端都設(shè)置有透明有機(jī)玻璃管,用于觀察冰漿流型。

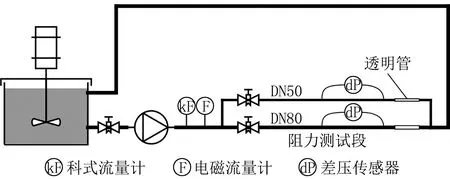
圖1 冰漿阻力實驗臺

冰漿的質(zhì)量流量由科式流量計測量,科式流量計還可以在線測量冰漿密度,由此可計算出含冰率。此外,實驗臺還設(shè)置了電磁流量計以測量冰漿的體積流量。實驗發(fā)現(xiàn),電磁流量計直接測量的體積流量與科式流量計經(jīng)密度換算后得到的體積流量相差無幾,這表明電磁流量計仍適用于冰漿的體積流量測量。這為實際工程應(yīng)用提供了冰漿測量的廉價方案,即可以用電磁流量計搭配在線密度計來測量冰漿流量和含冰率,以替代昂貴的科式流量計。阻力測量采用差壓傳感器,為盡可能消除水力入口效應(yīng)的影響,差壓傳感器的高壓測點(diǎn)距離直管入口1.5 m,滿足湍流水力入口段長徑比10的要求[16]。測量段長度為1 m,小流量下阻力可能只有數(shù)百Pa,而大流量下又會達(dá)到數(shù)千Pa,為應(yīng)對不同流量,實驗準(zhǔn)備了500 Pa和5 000 Pa 2種量程的差壓傳感器。

實驗所用的儀器參數(shù)見表1。

表1 實驗儀器參數(shù)

2 結(jié)果與討論

2.1 DN50管阻力特性

DN50管的實驗獲得了2組穩(wěn)定的含冰率,分別為8%和16%,對應(yīng)冰漿密度分別為987 kg/m3和993 kg/m3。在每組含冰率下,通過漿體泵變頻獲得不同的流量。在8%含冰率實驗組中,體積流量從9.51 m3/h逐步增大至27.17 m3/h,流速從1.24 m/s增大至3.55 m/s,雷諾數(shù)從36 111增大至103 135,相應(yīng)地,比摩阻從392 Pa/m增大至2 113 Pa/m,阻力系數(shù)從0.026 6降至0.017 7。在16%含冰率實驗組中,體積流量從10.3 m3/h逐步增大至27.73 m3/h,流速從1.35 m/s增大至3.63 m/s,雷諾數(shù)從39 089增大至105 246,比摩阻從425 Pa/m增大至2 211 Pa/m,阻力系數(shù)從0.024 5 降至0.017 6。

當(dāng)實驗進(jìn)行較長時間后,攪拌罐中的冰晶已融化殆盡,最后只剩下0 ℃的水,借此條件又測試了0 ℃水的阻力特性,以與冰漿實驗結(jié)果及單相流阻力關(guān)聯(lián)式進(jìn)行對照。實驗測試中水流量從7.47 m3/h逐步增大至27.81 m3/h,比摩阻從233 Pa/m增大至2 183 Pa/m,阻力系數(shù)從0.025 4降至0.017 2。

本實驗涉及的流動形式均為湍流。對于光滑管,單相湍流流動的阻力系數(shù)滿足Blasius關(guān)聯(lián)式:

f=0.316Re-0.25

(1)

式中f為阻力系數(shù);Re為基于載流體(即0 ℃水)物性計算的雷諾數(shù),有些文獻(xiàn)將其命名為參考雷諾數(shù)(reference Reynolds number)。

對于粗糙管,適用Colebrook關(guān)聯(lián)式:

(2)

式中ε為絕對粗糙度,mm,按新管取值0.01 mm;D為管徑,mm。

這2個關(guān)聯(lián)式都適用于Re>4 000的湍流光滑區(qū),前者在Re<105具有較高精度,后者還可以拓展到湍流過渡區(qū)和湍流粗糙區(qū)[17]。

在工程應(yīng)用中,比摩阻s(即單位流動長度的壓降)能更直觀地反映沿程阻力特性,它與阻力系數(shù)的關(guān)系如下:

(3)

式中ρ為流體密度,kg/m3;u為流速,m/s。

將以上0 ℃水、8%冰漿、16%冰漿的實驗結(jié)果繪制在圖2、3中,并與2個關(guān)聯(lián)式計算結(jié)果進(jìn)行對照,其中,關(guān)聯(lián)式的計算是基于0 ℃水的物性。從圖2來看,水及2種含冰率下冰漿的比摩阻實驗結(jié)果都與Blasius曲線吻合得很好,而Colebrook曲線在高雷諾數(shù)下逐漸偏離Blasius曲線。從圖2的比摩阻數(shù)據(jù)中很難看出各實驗組阻力特性之間的差異,圖3的阻力系數(shù)則將這種很小的差異進(jìn)行了放大。由圖3可以看到,在低雷諾數(shù)下,冰漿的阻力系數(shù)明顯大于水,而且含冰率越高,阻力系數(shù)越大,在這一區(qū)域,水的數(shù)據(jù)點(diǎn)仍基本落在Blasius曲線上,而冰漿的數(shù)據(jù)點(diǎn)明顯偏離Blasius曲線。

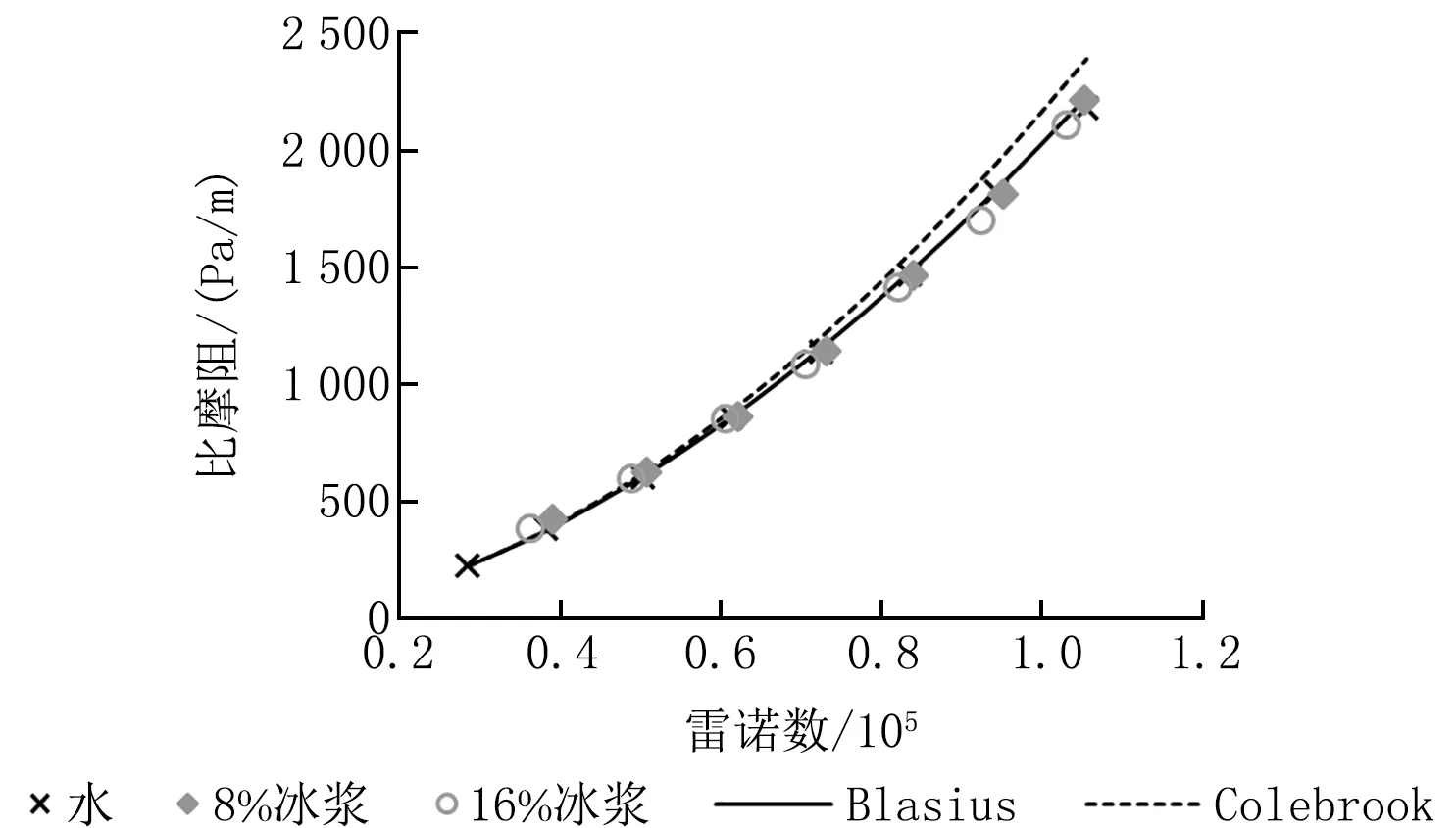
圖2 DN50管比摩阻與雷諾數(shù)的關(guān)系

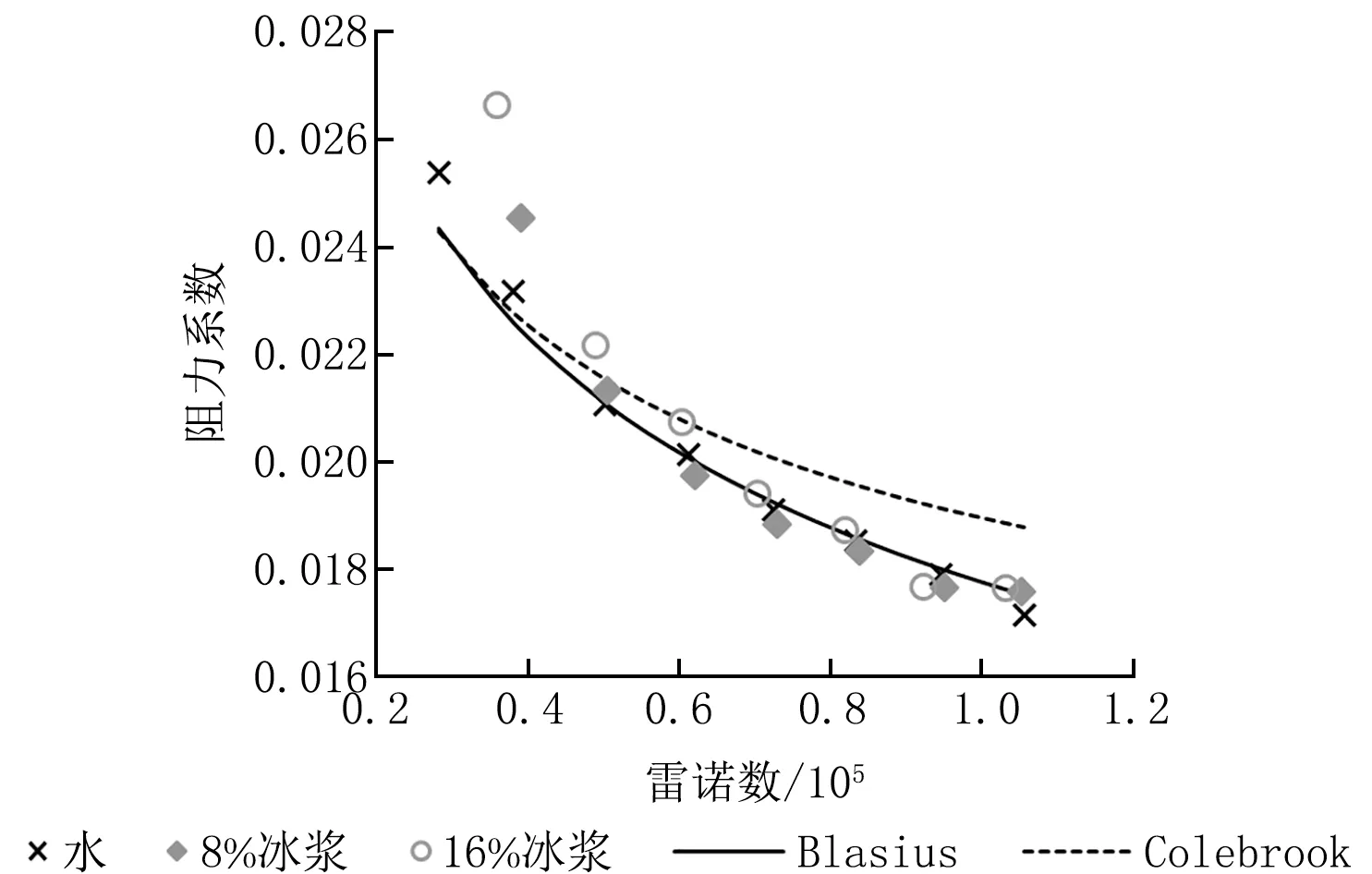
圖3 DN50管阻力系數(shù)與雷諾數(shù)的關(guān)系

由于實驗得到的是離散點(diǎn),為了定量判斷冰漿阻力系數(shù)何時進(jìn)入Blasius曲線,本文對實驗數(shù)據(jù)進(jìn)行了擬合,獲得了不同含冰率下冰漿阻力系數(shù)與雷諾數(shù)的指數(shù)關(guān)系式。

含冰率8%:

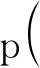
(4)

含冰率16%:

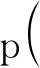
(5)

擬合相關(guān)系數(shù)分別為0.996 92和0.990 06。將以上擬合結(jié)果繪制成曲線,如圖4所示。以阻力系數(shù)偏差小于5%作為判定標(biāo)準(zhǔn),8%和16%冰漿分別在雷諾數(shù)為4.47×104和5.16×104時其阻力系數(shù)開始進(jìn)入Blasius曲線。

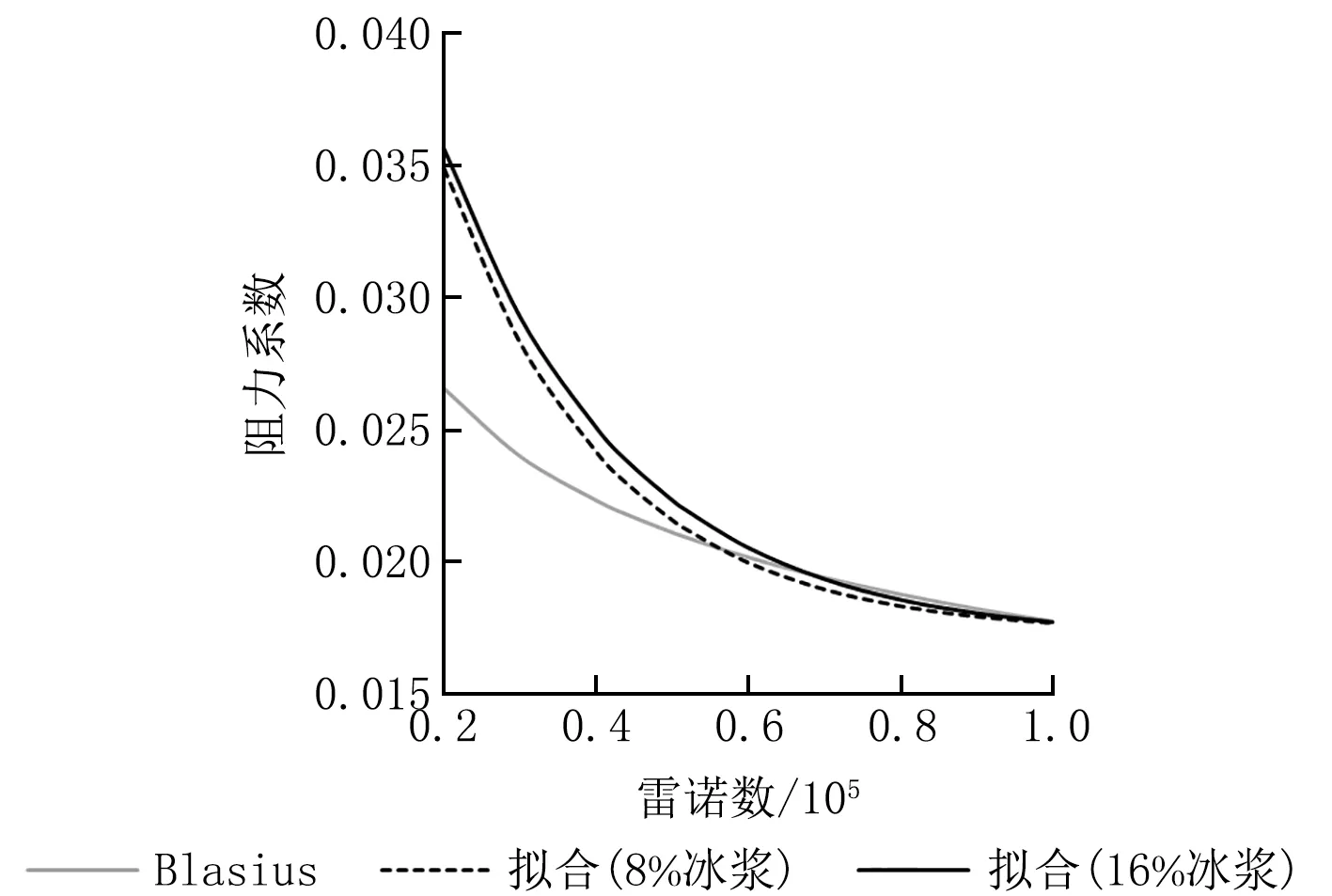
圖4 DN50管的冰漿阻力系數(shù)擬合曲線

2.2 DN80管阻力特性

在DN80管的實驗中,獲得了2組穩(wěn)定的含冰率,分別為6%和13%,對應(yīng)的冰漿密度分別為995 kg/m3和989 kg/m3。實驗結(jié)果見圖5、6。本組實驗中,雷諾數(shù)大部分都在5.00×104以上,最高達(dá)到1.32×105。從圖5、6可以看到:無論是比摩阻還是阻力系數(shù),Colebrook曲線都與實驗數(shù)據(jù)點(diǎn)及Blasius曲線偏離顯著;與DN50管一樣,水的數(shù)據(jù)點(diǎn)仍與Blasius曲線吻合得很好;在低雷諾數(shù)(5.00×104以下)下,冰漿的阻力系數(shù)遠(yuǎn)高于Blasius曲線,而隨著雷諾數(shù)增大,各組含冰率的阻力系數(shù)都逐漸落入Blasius曲線。

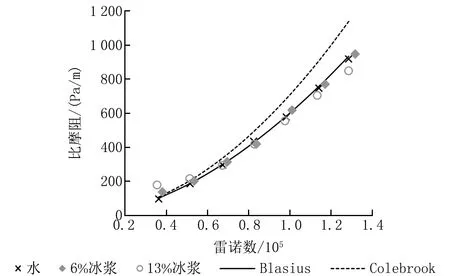
圖5 DN80管比摩阻與雷諾數(shù)的關(guān)系

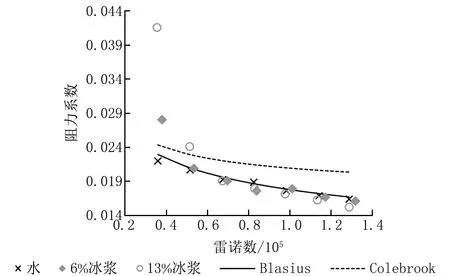
圖6 DN80管阻力系數(shù)與雷諾數(shù)的關(guān)系

將DN80管的冰漿阻力系數(shù)實驗數(shù)據(jù)擬合成指數(shù)關(guān)系式。

含冰率6%:

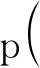
(6)

含冰率13%:

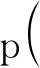
(7)

擬合相關(guān)系數(shù)分別為0.975 56和0.993 23。將以上擬合結(jié)果繪制成曲線,如圖7所示。仍以阻力系數(shù)偏差小于5%作為判定標(biāo)準(zhǔn),6%和13%冰漿分別在雷諾數(shù)為5.13×104和5.81×104時其阻力系數(shù)開始進(jìn)入Blasius曲線。

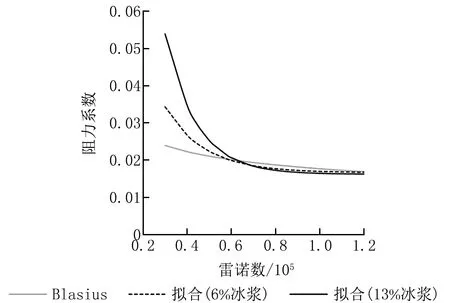
圖7 DN80管的冰漿阻力系數(shù)擬合曲線

2.3 直管阻力實驗結(jié)果分析

綜合以上實驗與關(guān)聯(lián)式對照結(jié)果,可以得出結(jié)論:在低雷諾數(shù)(但仍是湍流)下,冰漿的阻力系數(shù)遠(yuǎn)大于水的阻力系數(shù)(亦即Blasius計算值);在高雷諾數(shù)下,冰漿的阻力系數(shù)基本與水一致,與Blasius曲線吻合。這可以解釋為:在低雷諾數(shù)下,冰漿流動呈現(xiàn)出固液兩相分層流的特征,浮力相較于慣性力而言占主要部分,更多的冰晶顆粒懸浮在管道上部,冰晶與上壁面碰撞頻繁,故而阻力顯著大于水;在高雷諾數(shù)下,冰漿表現(xiàn)為均質(zhì)流,冰晶較為均勻地懸浮在整個截面,冰晶與壁面碰撞頻率較低,此時冰漿的流動與單相流基本無異,故與單相流的Blasius曲線吻合。

關(guān)于冰漿阻力系數(shù)何時開始進(jìn)入Blasius曲線,從實驗結(jié)果來看,含冰率越大則進(jìn)入Blasius曲線時的雷諾數(shù)越大,這與文獻(xiàn)[11]中的實驗數(shù)據(jù)是一致的,如圖8a所示。至于不同管徑,由于本研究中DN50管和DN80管實驗的含冰率并不一致,前者是8%和16%,后者是6%和13%(含冰率均低于前者),前者進(jìn)入Blasius曲線的雷諾數(shù)分別為4.47×104和5.16×104,后者則是5.13×104和5.81×104。由此可以推斷,管徑越大則越晚進(jìn)入,這也與文獻(xiàn)[11]中的實驗數(shù)據(jù)一致,如圖8b所示。文獻(xiàn)[11]中涉及的管徑最大為35.7 mm,在最高26%的含冰率下,進(jìn)入Blasius曲線的雷諾數(shù)大約為3×104。

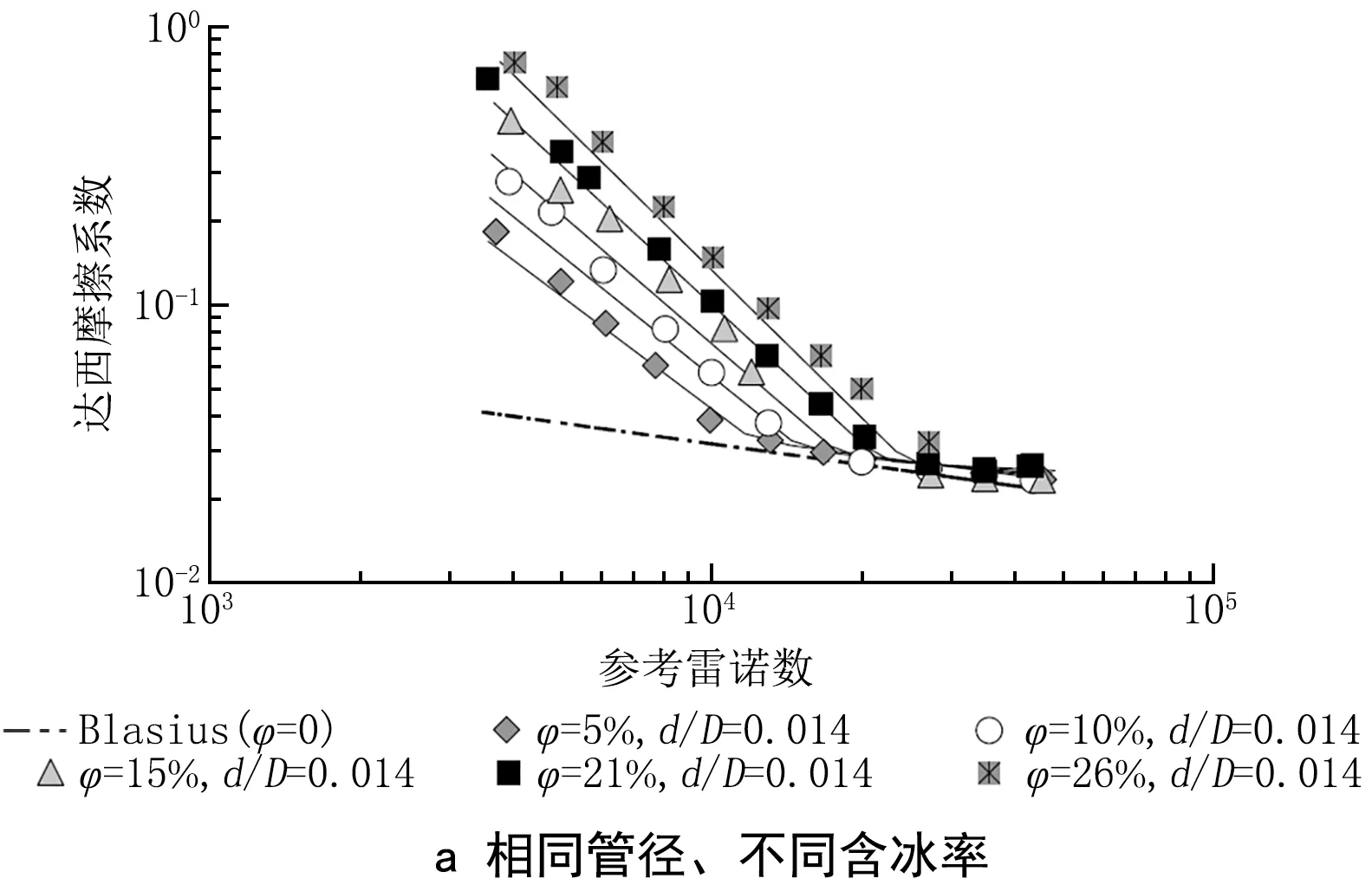
注:φ為含冰率;d為冰晶粒徑(0.5 mm)。

2.4 冰漿堵塞實驗結(jié)果與分析

冰漿在低流速下容易形成分層,冰晶顆粒上浮而聚集,最后形成靜止床而造成管道堵塞,這是冰漿應(yīng)用的最大障礙。通常,直管只要保證一定流速就能避免堵塞。在實驗中,測試的直管段始終未出現(xiàn)堵塞的情況,這也符合Bordet等人給出的直管臨界流速建議[13]。然而,對于彎頭而言,由于固液離心力差異,冰漿更容易形成分層而造成堵塞。由于實驗管路是一個環(huán)路,管路中正好設(shè)有90°DN80彎頭,故本文借此條件對彎頭的堵塞特性進(jìn)行了研究。通過不斷調(diào)小流量,找到從暢通到開始出現(xiàn)堵塞的臨界流速,判斷堵塞的依據(jù)則是流量出現(xiàn)劇烈波動。按照該方法,實驗獲得了彎頭在不同含冰率下的臨界流速,如圖9所示。由圖9可見,含冰率越大,則臨界流速越大,臨界流速與含冰率近似呈線性關(guān)系。另外,實驗還發(fā)現(xiàn),在彎頭出現(xiàn)堵塞的流速下,直管仍是暢通的,驗證了彎頭更容易堵塞。

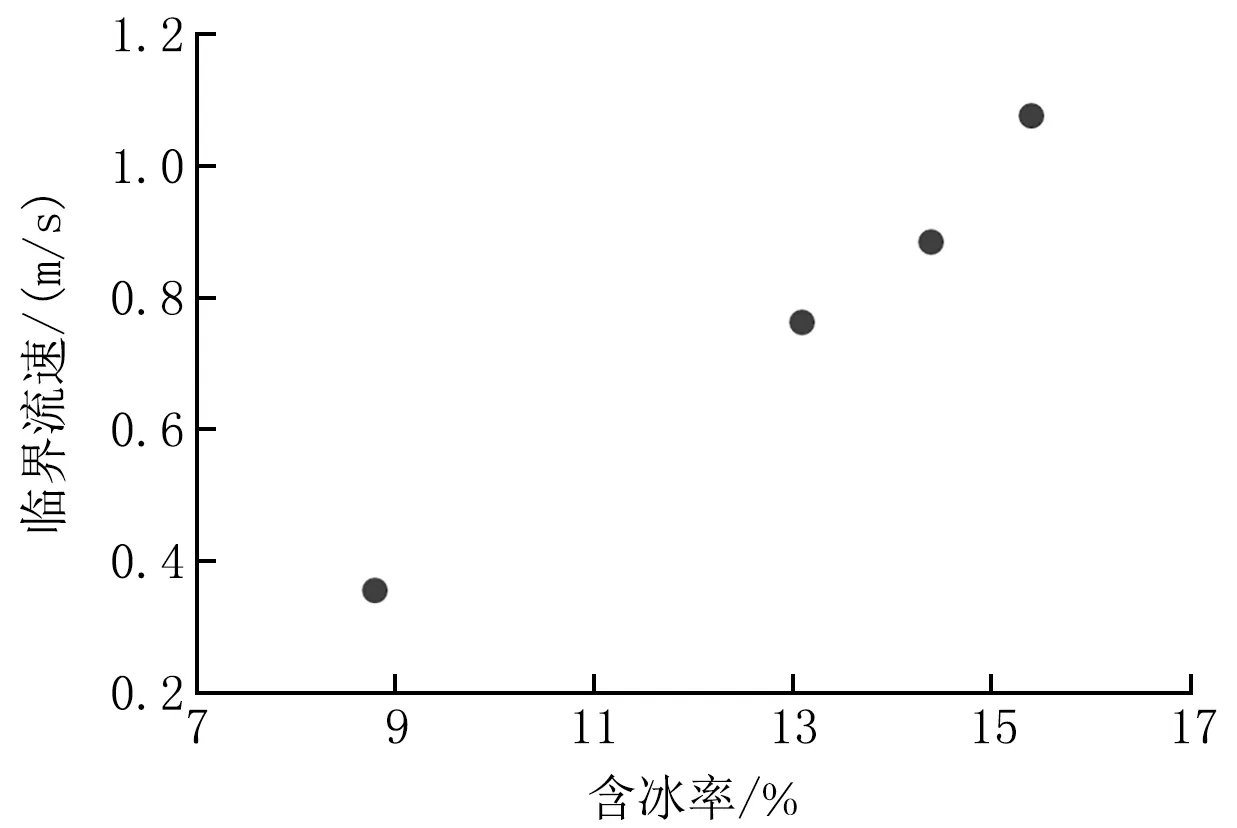
圖9 彎頭的臨界流速與含冰率的關(guān)系

3 結(jié)論

本文針對DN50和DN80 2種大管徑管道開展了冰漿流動阻力特性實驗研究,實驗均處于湍流。得到以下結(jié)論:

1) 在低雷諾數(shù)下,冰漿阻力系數(shù)遠(yuǎn)大于適用于純水單相流的Blasius關(guān)聯(lián)式計算值,且含冰率越大,阻力系數(shù)越大。

2) 在高雷諾數(shù)下,冰漿的阻力特性符合Blasius關(guān)聯(lián)式,不同含冰率下的阻力系數(shù)都與純水一致。

3) 含冰率和管徑對冰漿阻力系數(shù)何時進(jìn)入Blasius曲線有影響,含冰率越大、管徑越大,則開始進(jìn)入Blasius曲線的雷諾數(shù)越大。

4) 相較于直管,彎頭的臨界流速更高,更容易出現(xiàn)堵塞,且含冰率越大,則臨界流速越大。

本文的研究可為DN50～DN80級別的大管徑管道冰漿輸送提供技術(shù)參考,從目前實驗結(jié)果所反映的規(guī)律來看,本文的研究結(jié)論可拓展到更大管徑,在更大的管徑下,冰漿流動即使在不大的流速下也能達(dá)到很大的雷諾數(shù),阻力特性符合Blasius關(guān)聯(lián)式。考慮到搭建更大尺度的實驗臺具有一定難度,現(xiàn)計劃開展CFD研究,以本文的實驗結(jié)果驗證或修正固液兩相流模型,而后針對更大管徑的冰漿流動開展CFD仿真,這將是下一步的研究工作。