公路隧道射流風機布置參數(shù)研究綜述

馬占海 徐 瑩 張錦秋 劉賢鵬 馬立剛

(1.河北省高速公路延崇籌建處,張家口;2.河北工業(yè)大學,天津)

0 引言

隨著我國公路交通網(wǎng)絡的不斷發(fā)展與完善,長隧道、特長隧道的建設和運營愈來愈多。隧道建設規(guī)模不斷增大,使污染物更易積聚于隧道內(nèi),成為影響隧道安全運營的重要因素。因此,通風系統(tǒng)對降低隧道內(nèi)污染物濃度、保障隧道安全運營十分重要[1-2]。

常見的隧道通風方式有自然通風[3-4]、橫向通風[5]和縱向通風[6]。橫向通風有全橫向和半橫向通風2種形式。橫向通風需要在隧道內(nèi)設置道板、吊頂和風井,增加了隧道建設工程量;且通風阻力較大,增大了隧道運營成本[7]。采用射流風機誘導的縱向通風可以有效利用隧道通行車輛產(chǎn)生的活塞風,具有工程造價低、設備簡單、使用方便等優(yōu)點[8-9]。世界道路協(xié)會(PIARC)調(diào)查發(fā)現(xiàn),所調(diào)查的27條隧道中,超過70%采用縱向通風方式[10]。縱向通風已成為公路隧道的主要通風方式[11]。

縱向通風的通風效率取決于射流風機產(chǎn)生空氣射流的誘導和升壓效應。在實際隧道中,射流風機通常安裝于隧道頂壁附近。由于科恩達效應(Coanda effect),導致空氣射流吸附于隧道頂板,從而產(chǎn)生較大的壁面剪應力[12],造成動量損失而影響射流風機的升壓效應。因此,國內(nèi)外學者對射流風機的最佳安裝參數(shù)進行了研究,如射流風機俯仰角[13]、偏轉角[11],并取得了諸多研究成果。

JTG/T D70/2-02—2014《公路隧道通風設計細則》[14]規(guī)定了射流風機選型和布置部分參數(shù),但并未對參數(shù)的推導和影響規(guī)律作出解釋。本文對公路隧道射流風機布置參數(shù)的相關研究進行了綜述,從通風射流特性及通風質(zhì)量評價參數(shù)出發(fā),總結了直線與曲線公路隧道射流風機縱向和橫斷面布置重要參數(shù)及其影響規(guī)律。其中,風機射流俯仰角和偏轉角研究的總結,豐富了JTG/T D70/2-02—2014《公路隧道通風設計細則》的相關內(nèi)容,可為公路隧道縱向通風射流風機的布置提供參考,有利于隧道運營通風的優(yōu)化設計和能源節(jié)約。

1 通風射流特性及通風質(zhì)量評價

1.1 通風射流特性

通風射流具有誘導特性和增壓特性。隧道射流通風的誘導和升壓作用使隧道內(nèi)氣流定向流動,實現(xiàn)隧道通風。

射流風機發(fā)出的高速射流受前方隧道氣流的阻力作用,致使部分氣體沿隧道下部向后流動產(chǎn)生旋渦,射流微團產(chǎn)生的橫向脈動與隧道氣流進行能量交換,實現(xiàn)對隧道氣流的“卷吸”。“卷吸”作用使射流影響范圍擴大,流量增加;隧道低速氣流的加入,使得射流速度減小,壓力上升。直至射流充分發(fā)展前,整個隧道氣流沿縱向呈現(xiàn)一種漸變的、非均勻的逆壓流動。射流充分發(fā)展后,伴隨流消失,斷面速度趨于均勻[15]。圖1為隧道內(nèi)射流風機啟動后速度流場分布圖[16]。風機啟動30 s后,在風機前下方出現(xiàn)明顯渦流,如圖1a所示;射流充分發(fā)展后,隧道內(nèi)速度形成穩(wěn)定定向流,如圖1b所示。

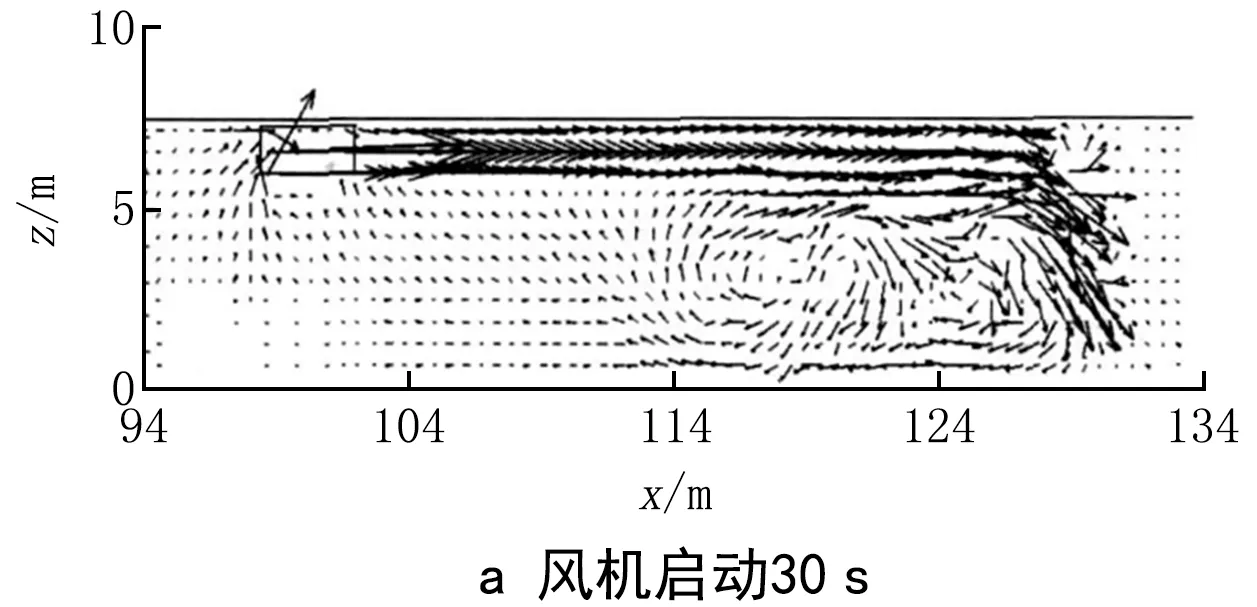
圖1 風機啟動后隧道內(nèi)流場矢量圖

射流通風是射流動能轉化為勢能的過程。在風機工作面末端,斷面速度分布均勻,湍動強度趨于穩(wěn)定,射流風機組升壓力最高[17]。單臺射流風機的升壓力可表示為[14]

(1)

式中 Δpj為單臺射流風機的升壓力,Pa;ρ為計算點的空氣密度,kg/m3;vj為射流風機的出風口速度,m/s;Aj為射流風機出風口面積,m2;Ar為隧道凈空斷面積,m2;vr為隧道設計風速,m/s;η*為射流風機位置摩擦阻力損失折減系數(shù)。

1.2 通風質(zhì)量評價

為評價隧道通風質(zhì)量,研究者提出了多種通風質(zhì)量評價指標,如斷面平均風速、風機升壓折減系數(shù)、空氣齡[17-18]。

隧道射流通風中,因隧道斷面面積較大,風速分布往往不均勻,通常采用斷面平均速度分布對通風射流發(fā)展狀態(tài)進行定量評價。

風機升壓折減系數(shù)η是衡量風機升壓能力的重要指標,部分文獻稱之為風機升壓綜合影響系數(shù)K,其表達式為

(2)

式中 Δpaj為實際升壓力,由實際測量或數(shù)值計算得到,Pa。

η或K值越大,表明風機實際升壓力值與理論值越接近,風機通風效果越好。王旭等人基于現(xiàn)場實測和數(shù)值計算,揭示了海底隧道腐蝕環(huán)境下風機升壓力衰減機理并建立了風機升壓力的計算方法[19]。

空氣齡指空氣進入空間后經(jīng)歷的時間,能夠反映空間內(nèi)的氣體流動模式和通風效果。與之相關的指標有換氣率、換氣指數(shù)等。

2 風機組縱向布置參數(shù)

2.1 縱向控制間距理論計算

射流的充分發(fā)展是射流風機實現(xiàn)高效通風的重要條件。若風機組縱向間距過小,隧道內(nèi)尚未形成均勻流速,將會影響下一組射流風機的工作性能[18,20]。為提高隧道射流通風效率,保障射流充分發(fā)展與風機的正常工作,射流風機間應保持合理的縱向控制間距。

孫三祥等人提出了風機組縱向控制間距的計算方法[21]。依據(jù)射流通風系統(tǒng)的單元流動模式(如圖2所示),將風機組的縱向控制間距l(xiāng)mc表示為

圖2 射流通風系統(tǒng)的單元流動模式

lmc=lj+lst=lsu+lin+lst

(3)

式中l(wèi)j為射流風機工作段長度,m;lst為兩工作段之間的穩(wěn)定段長度,m;lsu為吸入段長度,m;lin為誘導長度,m。

依據(jù)吸風口的流場特性和試驗結果,確定吸入段長度lsu=1.5D,穩(wěn)定段長度lst≥2D(D為隧道斷面當量直徑)。

射流誘導長度lin是風機射流主要幾何特性的定量描述,其回歸方程為

lin=(7.16+62.93α-108.20mβ)D

(4)

式中α為速度比,α=vr/vj;m為斷面風機臺數(shù);β為面積比,β=Aj/Ar。

風機組的縱向控制間距可整理為

lmc=(9.5+63α-108mβ)D

(5)

2.2 縱向控制間距分析

依據(jù)射流風機的流場特征,總結出射流充分發(fā)展的風機工作段末端呈現(xiàn)出以下特性[21]：1) 斷面氣流速度分布均勻;2) 湍流強度趨于穩(wěn)定;3) 風機工作段末端對應射流最高升壓面。因此,射流風機最小縱向間距可通過隧道斷面速度、湍流強度和最高升壓面位置確定。

楊秀軍等人基于射流力學有關原理得出:風機口徑、射流風機軸線之間的距離及隧道設計風速影響射流風機組的縱向最小間距;射流風機口徑越大,射流縱向充分發(fā)展的距離越大。同時,推導了風機組縱向控制間距計算方法;依據(jù)射流風機工作段末端特性,確定射流風機工作段的最小距離為110 m,與理論計算解基本相同[17]。

李曉菲等人建立了橫斷面布置2臺射流風機的隧道CFD模型,依據(jù)射流風機工作段末端特性,確定了射流風機誘導段長度和風機縱向控制間距,并與式(5)理論解對比,驗證了數(shù)值分析的準確性[22]。此外,李曉菲等人采用升壓綜合影響系數(shù)K評估了不同射流風機縱向控制間距l(xiāng)mc的通風效果[22],如圖3所示。升壓綜合影響系數(shù)K值愈接近1,風機組實際升壓力值與理論壓力值愈接近,即風機組性能愈佳。由圖3可以看出,當風機縱向控制間距為100～115 m時,隧道射流通風效果最好。隨著風機縱向控制間距的增大,射流通風效果明顯降低。

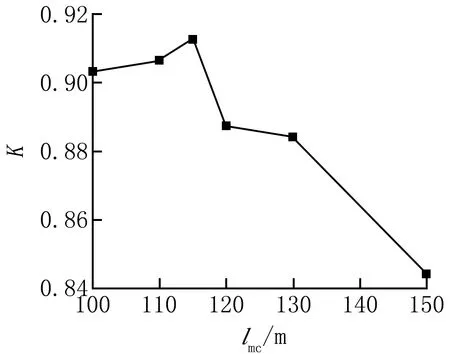
圖3 風機縱向控制間距l(xiāng)mc與升壓綜合影響系數(shù)K關系曲線[22]

Liu等人通過搭建物理模型試驗平臺,模擬了汾水嶺長隧道通風系統(tǒng),結果表明,所提出的射流風機布置方案能滿足短期設計風速需求[1]。

3 風機組橫斷面布置參數(shù)

3.1 風機橫向間距

為方便隧道射流風機的管理與維護,在隧道同一斷面內(nèi)通常布置2臺或多臺射流風機。除風機組縱向控制間距外,射流的誘導和升壓效應也受風機橫向間距影響。

風機出口處的射流相互卷吸和干擾,直至融合為一股射流,最終與隧道內(nèi)氣流完全混合,形成穩(wěn)定定向流[16]。雙股射流流動特征如圖4所示[23],射流融合前的發(fā)展區(qū)域為會聚區(qū),初始融合點為自由滯點,射流融合后形成聯(lián)合區(qū),并穩(wěn)定流動。

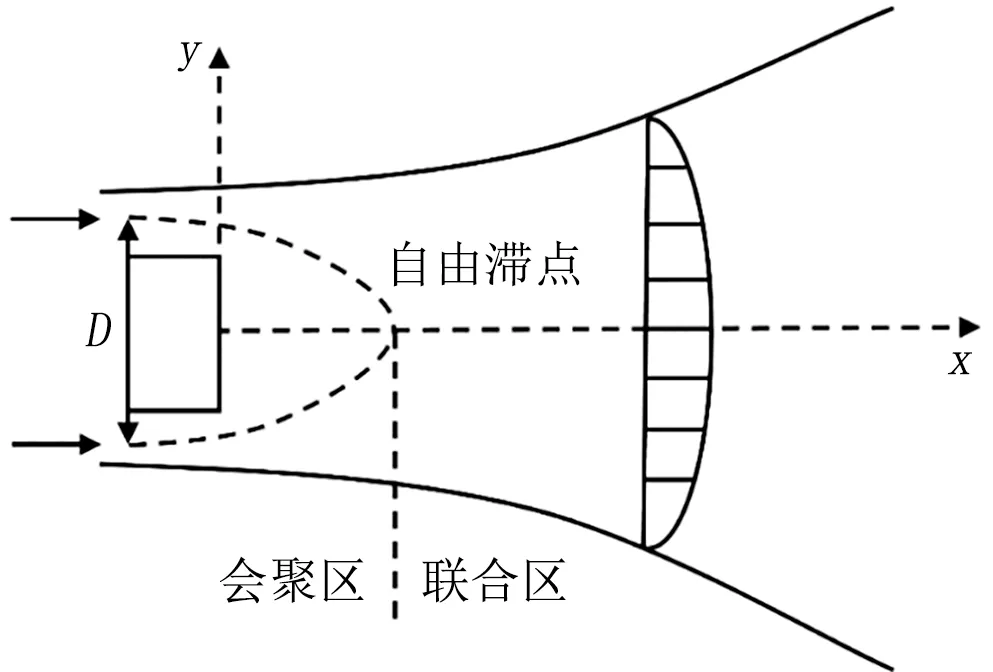
圖4 雙股射流基本流動特征[23]

風機組橫向間距過小時,射流橫向影響范圍小,隧道氣流未能通過射流微團產(chǎn)生的橫向脈動進行動量與能量交換,不能有效誘導隧道氣流[24];同時,自由滯點靠近風機出口,射流縱向影響范圍小,射流風機升壓力降低。風機組橫向間距過大時,風機與隧道側壁的距離接近,壁面摩擦阻力降低射流動能,射流不能會聚,隧道氣流較難達到平穩(wěn),射流升壓力減小[25]。

方勇等人通過CFD數(shù)值模擬計算得出,三車道公路隧道射流風機的橫向間距為風機橫斷面直徑的3～4倍時,射流風機升壓效果好,此時風機距離變化對升壓力的影響較小[26]。徐志勝等人通過比較風機不同橫向間距的升壓折減系數(shù),確定風機最佳橫向間距為3D(見圖5),并通過比較不同風機橫向間距下隧道內(nèi)污染物質(zhì)量分數(shù)分布,進一步驗證了最佳橫向間距布置下射流風機的通風效果[27]。此外,盧毅等人基于數(shù)值計算結果,通過分析風機升壓折減系數(shù)的變化,確定了太湖隧道的射流風機最優(yōu)橫向凈間距為2.0D～2.4D[20]。

圖5 升壓折減系數(shù)分布曲線[27]

3.2 風機安裝高度

射流風機的通風效果取決于射流在隧道內(nèi)是否得到充分發(fā)展,足夠的射流空間是射流充分發(fā)展的重要條件。JTG/T D70/2-02—2014《公路隧道通風設計細則》規(guī)定,風機安裝高度不應侵入建筑限界,邊沿與隧道建筑限界凈距離應不小于15 cm[14]。為進一步確定風機安裝最佳高度,部分學者對風機不同安裝高度下的射流通風效果進行了研究。

趙黎等人依據(jù)明堂山隧道的結構參數(shù),建立了500 m長隧道的CFD模型,模擬計算了風機安裝高度距建筑限界頂部15、30、45、60 cm工況下風機的通風效果[28]。不同風機安裝高度下隧道的升壓力見表1。可以看出,隨著風機距建筑限界頂部距離的增大,風機提供的升壓力減小,升壓綜合影響系數(shù)K逐漸減小。

表1 風機安裝高度對升壓力的影響[28]

同時,隨著風機距建筑限界頂部距離的增加,即風機安裝高度的增加,出口射流受到隧道拱頂?shù)南拗?沒有足夠的擴展空間。高速氣流沖擊拱頂和隧道壁面摩擦阻力共同作用導致射流動能大量損失,射流無法推進,風機出口附近風速減小,如圖6所示[28]。

圖6 不同風機安裝高度下出口處速度云圖[28]

盧毅等人建立了具有3臺橫向布置風機的方形截面隧道模型,通過風機軸線速度變化和升壓綜合影響系數(shù)評估了風機安裝高度對通風效果的影響。圖7為風機軸線速度分布圖,圖8為風機升壓力和升壓綜合影響系數(shù)曲線圖。結果表明,風機距隧道頂壁距離越大,出口附近風速越大,風機升壓力越大,升壓綜合影響系數(shù)越高。當風機距隧道頂壁距離為1.2D～1.4D時,風機升壓綜合影響系數(shù)為0.887～0.931[20]。

圖7 風機軸線剖面速度變化云圖[20]

圖8 風機距隧道頂壁不同距離時升壓力和 升壓綜合影響系數(shù)變化[20]

3.3 風機射流角度

射流風機通常安裝于隧道頂部,為減小風機出口處高速氣流沖擊隧道壁面的動能損耗,部分學者在直線隧道和香蕉型隧道射流風機[29]安裝形式的基礎上,開展了風機安裝角度對隧道通風效果影響的研究,驗證了風機射流角度的調(diào)整可以有效減弱科恩達效應(Coanda effect)對射流發(fā)展的影響[30],從而顯著降低通風系統(tǒng)的能耗[31]。

Betta等人采用CFD方法分析了不同風機俯仰角工況的通風效果。圖9為射流風機安裝角度示意圖。最佳俯仰角可以最大限度地減小流動附著引起的壓力損失,提高通風效率,節(jié)約能源。圖10為射流風機不同安裝俯仰角下風機平面速度分布云圖,可以看出,隨著風機安裝俯仰角的增大,風機射流趨向于隧道底板。Betta等人比較了風機不同安裝俯仰角下隧道頂壁和底板的剪應力,以及推力和推力變化率,確定θ=6°為最佳安裝角度。對于交通阻塞工況,風機安裝最佳俯仰角為2°～4°[32]。

圖9 射流風機安裝示意圖[32]

圖10 不同俯仰角θ下風機平面速度分布云圖[32]

吳珂等人基于Fluent數(shù)值計算軟件,建立了橫向布置3臺射流風機的隧道模型,分析了風機射流風速為30 m/s時,不同安裝角度下的風機升壓綜合影響系數(shù)(見表2)。可以看出:安裝角度為0°～11°時,升壓綜合影響系數(shù)逐漸增大;當安裝角度大于11°時,升壓綜合影響系數(shù)逐漸減小。這是因為當安裝角度為11°時,射流微團與隧道壁面的摩擦阻力損失最小;而安裝角度大于11°時,射流風機在出口處形成的旋渦不斷增大,導致升壓綜合影響系數(shù)下降。因此,風機最佳安裝角度為11°[33]。

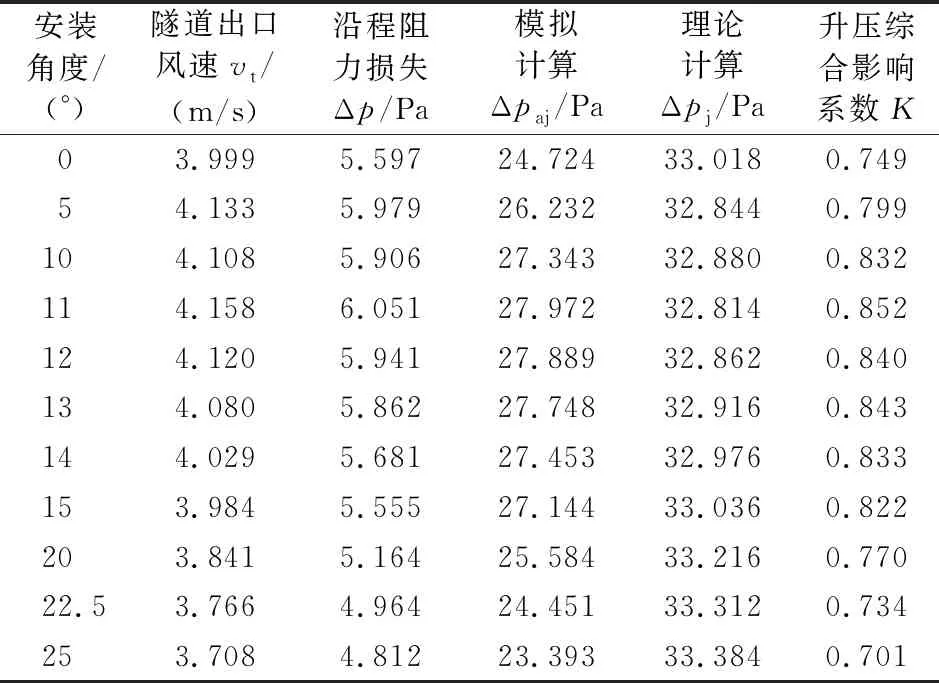
表2 不同安裝角度下單臺風機升壓綜合影響系數(shù)

Zhao等人通過平均空氣齡和升壓系數(shù)確定射流風機的最佳俯仰角。圖11為射流風機不同俯仰角下,隧道側壁縱斷面空氣齡等高線和流線分布。當射流風機安裝俯仰角為7°時,隧道凈空空間的平均空氣齡較小,升壓折減系數(shù)最大。因此確定射流風機最佳安裝俯仰角為7°[34]。

圖11 隧道側壁縱斷面空氣齡等高線和流線分布[34]

4 曲線隧道風機安裝參數(shù)

與直線隧道不同,曲線隧道斷面速度分布的不均勻性和隧道壁面的變化使射流擴散過程更加復雜,影響隧道的通風效率。射流的誘導和增壓特性在曲線隧道依然存在,但曲線隧道內(nèi)射流沖擊壁面導致射流動量嚴重損失,射流風機的通風效率降低。適當調(diào)整風機安裝參數(shù)是保證曲線隧道通風效率的有效方法。

王峰等人建立了半徑600 m、長度330 m的曲線隧道模型,對比了曲線隧道內(nèi)風機組橫斷面及縱向布置方式的通風效果,分析結果表明,并列風機組向隧道內(nèi)側移動0.5 m、風機間距2.4 m時,風機折減效率最大為85.2%,曲線隧道風機組縱向誘導距離為90 m[35]。

陳研等人建立了如圖12所示的2段曲線隧道CFD數(shù)值模型,優(yōu)化曲線隧道風機組橫斷面和縱向布置。不調(diào)整風機安裝位置時,風機射流沖擊隧道壁面,隧道內(nèi)部流場存在大面積低速區(qū),速度分布不均勻,不利于隧道通風。風機間距2D、內(nèi)側風機向外偏移D、偏轉10°時,隧道射流特性較好,如圖13所示。此時,F1和F2區(qū)段通風效果較好。圖14為隧道平面靜壓分布圖。射流在風機下游100 m發(fā)展穩(wěn)定,據(jù)此確定F1和F2區(qū)段風機縱向間距為100 m適宜[37]。

圖12 數(shù)值模型示意圖[37]

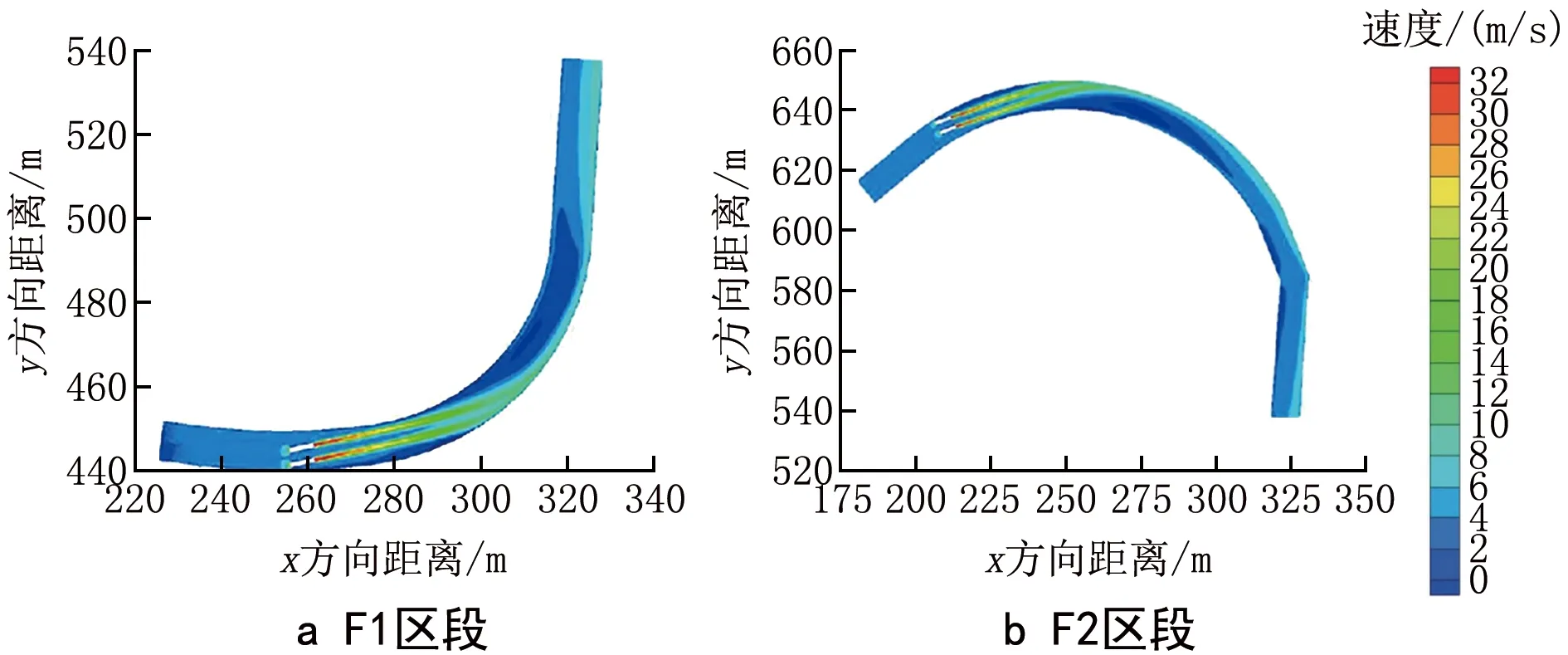
圖13 內(nèi)側風機向外偏移D、偏轉角度10°時 隧道內(nèi)空氣射流特性[37]

圖14 隧道斷面平均靜壓分布[37]

Chen等人采用CFD數(shù)值模擬方法,對隧道內(nèi)流場、升壓折減系數(shù)和壁面剪應力進行了對比分析,確定了300 m長彎曲隧道內(nèi)射流風機的最優(yōu)安裝位置。當射流風機向隧道凸壁面?zhèn)纫?.5 m或向凸壁面水平傾斜3°時,氣流附壁效應增強,射流縱向影響范圍擴大[38]。

5 結論與展望

隧道縱向通風中,射流風機的布置參數(shù)對射流的發(fā)展特性有較大影響,進而影響隧道通風效果。本文對公路隧道射流風機布置參數(shù)相關研究進行綜述,得到如下結論:

1) 射流風機組縱向控制間距可通過理論計算或數(shù)值模擬分析確定;風機口徑、風機軸線間距、隧道設計風速等因素影響風機組縱向控制間距。

2) 風機組橫向間距過小和過大時,風機升壓力均較小,通風效率差。

3) 在建筑限界范圍內(nèi),風機安裝在距隧道頂壁距離較大位置,可有效避免射流沖擊頂壁造成的動能損失,提高通風效率。

4) 隨著風機安裝俯仰角的增大,射流趨向于隧道底板;風機安裝最佳俯仰角的確定可以有效減小流動附著引起的壓力損失,提高通風效率。

5) 曲線隧道風機組的偏移位置和偏轉角度影響隧道通風效率;隧道曲率影響風機偏移和偏轉量。

目前,JTG/T D70/2-02—2014《公路隧道通風設計細則》中尚無射流風機安裝俯仰角及曲線隧道風機偏移位置、偏轉角度的相關規(guī)定。建議射流風機布置時考慮以上因素,以提高射流風機通風效率。

實際工程中,隧道通風系統(tǒng)的性能受諸多因素影響,如坡度、自然風[39]。射流風機安裝參數(shù)研究的實驗和仿真工況多為理想工況,與隧道內(nèi)射流風機的實際通風效果存在差異。例如,山區(qū)等多風區(qū)域的隧道通風系統(tǒng)會受到不同速度的自然風的影響。因此,應在今后的研究中進一步將隧道實際環(huán)境參數(shù)作為風機安裝參數(shù)研究的初始條件,以得到更為接近真實工況的研究結果。

受地形等多種因素影響,不同隧道的結構和通風系統(tǒng)設計存在較大差異。現(xiàn)有風機安裝參數(shù)的研究多具有針對性,難以直接推廣應用于其他隧道。因此,建立風機安裝參數(shù)與隧道結構、通風評價指標的參數(shù)化關系,有利于簡化隧道通風系統(tǒng)設計,提高隧道通風效率、節(jié)約能源。