裝配式預制構件市場信息價動態測算模型研究

李立巖，汪小南

（1.武漢市市政建設集團有限公司，湖北 武漢 430023；2.武漢市城市建設投資開發集團有限公司，湖北 武漢 430000；3.武漢市政工程設計研究院有限責任公司，湖北 武漢 430023）

0 引言

隨著裝配式建筑在我國的大力推行，預制構件使用量呈現上漲趨勢，其生產成本是裝配式建筑增量成本的主要增項[1]。為控制裝配式建筑成本及滿足市場定價的需求，各地建設行政主管部門先后建立了預制構件市場信息價發布機制。然而，當前預制構件信息價發布機制存在更新滯后、時效性差等問題，對預制構件市場的指導性作用較小，且滯后于現實需要。市場信息價作為規范預制構件市場、投標報價的主要依據，其準確性具有重要的現實意義。因此，亟須展開對預制構件市場信息價的及時動態測算方法研究來指導預制構件市場。

國內外學者對具有時間序列特征的價格預測問題進行了較為深入的研究，其選用的模型方法主要分為回歸模型、神經網絡模型、SVM 模型及灰色預測模型。Shanoli Samui Pal[2]、Mehmet Kabak 等[3-4]分別利用回歸模型、神經網絡對市場價格進行短期預測。這兩種方法雖然具有較高的預測精度，但均需要大量的歷史經驗數據。而針對小樣本數據的預測問題，一些學者[3，5-6]分別利用改進后的SVM 模型進行市場參考價格的預測，展現了SVM 算法在小樣本數據學習上的優越性，但預測模型的穩定性取決于核函數的選取。不依賴于樣本數據具有大量性、呈規律性分布特征的SCGM（1，1）c 預測模型展現了在時序數據預測上的特有優勢，有學者[7-9]利用馬爾科夫鏈、殘差修正等方法進一步優化SCGM（1，1）c 預測模型，不僅提升了SCGM（1，1）c 預測模型的預測精度，同時改善了數據少、隨機波動對預測精度的影響程度。相較于SCGM（1，1）c 預測模型，SVM 模型結構的復雜性決定了其對數據量的要求會更高，因此優化后的SCGM（1，1）c 預測模型更加適用于數據量少且存在隨機波動的預測工作。

而目前，各地建設行政主管部門關于預制構件的相關技術標準、管理體系還有待完善，市場信息價發布機制也處于初步建立階段，預制構件市場信息價及相關生產費用整體呈現出數據量偏少、隨機波動，以及變化受眾多因素影響等特征，適合與SCGM（1，1）c預測模型方法結合并開展研究。

鑒于此，本文擬選用SCGM（1，1）c 預測模型對預制構件市場信息價進行預測，并利用馬爾科夫鏈來優化改善數據隨機波動對模型預測精度的影響，實現預制構件市場信息價的及時、動態測算。同時，與另外3種常用的預測模型方法對比來驗證本文模型的優勢，為主管部門實現規范引導預制構件市場價格精細化管理提供技術支撐，并為類似預測工作提供參考。

1 預制構件市場信息價動態測算模型方法

預制構件市場信息價（MIP）代表地區當前的市場平均價格水平，主要選取市場上具有代表性的預制構件生產企業的實際費用數據作為參考標準進行制定，由人工費（Lc）、材料費（Mc）、機械費（Mf）、折舊及攤銷（Da）、深化設計費（Df）、運輸費（Tf）、管理費、利潤、稅金組成。其中，人工費、材料費、機械費占比較大，是預制構件生產價格變化的主因[10]。通過市場調研和相關人員訪談，在以月為時間跨度的周期內，預制構件市場信息價的波動主要為人工費、材料費、機械費（合稱直接費）的變化，折舊及攤銷、深化設計費、運輸費等在周期內基本無變化。

實現預制構件市場信息價的及時動態測算，需對周期內主要波動項數據的變化趨勢加以預測，并對非波動項數據進行周期測定。測算思路如下：

第一步：從預制構件綜合單價構成體系出發，建立預制構件市場信息價動態測算模型，如式（1）所示。

式中：t 表示月份；ic1表示管理費的費率；ic2表示利潤的費率；ic3表示稅金的稅率。其中，管理費、利潤取直接費的一定費率，稅金在綜合單價所有組成項的基礎上取一定費率得到。

第二步：通過建立馬爾科夫優化后的SCGM（1，1）c 預測模型實現對主要波動項的預測，得到第t 月份人工費預測值Lc（t）、材料費預測值Mc（t）、機械費預測值Mf（t）。

第三步：將主要波動項的預測值代入到式（1）中，結合對非波動項數據的周期測算，即可提前預測出第t 月份的預制構件市場信息價。待收集到各預制部件生產企業反饋的第t 月份的實際數據，即可實現第t+1 月份預制構件市場信息價的預測。如此進行，從而實現預制構件市場信息價的及時動態測算。

2 預測模型構建

2.1 建立S CGM（1，1）c 預測模型

系統云灰色模型SCGM（1，1）c 起源于灰色模型GM（1，1），主要針對“部分信息已知，部分信息未知”的“小樣本”“貧信息”為特征的研究對象，通過系列數學運算使其成為具有指數變化規律的數列。為改善GM（1，1）模型在復雜情形下的適用性，系統云（System Cloud）憑借其在面臨不確定性、多因子錯綜復雜行為預測上的優勢，兩者結合的SCGM（1，1）c預測模型在處理數據量少、波動明顯、情形復雜的預測工作中得到了大量使用，能最大限度的從自身尋找數據序列中的有用信息，探索內在規律。

面臨預制構件市場信息價相關數據偏少且存在隨機波動的實際狀況，構建主要波動項的SCGM（1，1）c 預測模型，操作過程如下：

（1）選取2022 年1—11 月份的人材機費用分別作為模型的原始時間序列矩陣X0，其中：

式中：x（0）（n）代表第n 個月的人工費、材料費、機械費數據。對原始序列進行相應處理得到均值序列xˉ（0）（k）[見式（2）]和積分生成序列xˉ（1）（k）[見式（3）]，其中k=2，3，…，n。

（2）SCGM（1，1）c 預測模型如式（4）所示。

式中：a、U 為參數。

于是，其一次響應函數為：

式中：x^（1）（1）=b-c，參數a、b、c 計算公式見式（6）～式（8）。

（3）對x^（1）（k）進行還原處理，得到擬合值x^（0）（k），具體見式（9）。

式中：x^（0）（k）為人材機費用數據的擬合值。

2.2 建立馬爾科夫優化后的S CGM（1，1）c 預測模型

馬爾科夫鏈是研究某一事件的狀態及狀態之間轉移規律的隨機過程理論[11]。它通過對某一時刻不同狀態的初始概率及狀態之間的轉移概率關系，來研究未來時刻狀態的變化趨勢，適用于存在隨機波動的數據預測工作。

利用馬爾科夫優化SCGM（1，1）c 預測模型的流程如圖1 所示。

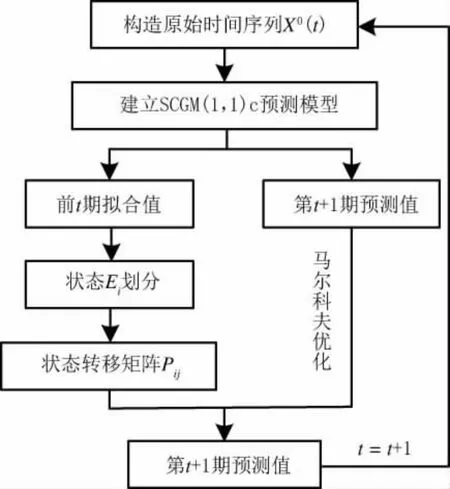
圖1 馬爾科夫優化S CGM(1,1)c 預測模型流程

具體操作步驟如下：

（1）狀態劃分。預制構件市場價格中人材機費用的變動沒有明顯的規律，灰精度指標Y（k）也是隨機的，計算公式見式（10）。將擬合精度劃分為m 個狀態，則可將任一狀態Ei表示為如式（11）所示。

（2）構建狀態轉移矩陣p（k）。因為人材機費用預測存在諸多不確定性，對未來較長時間進行預測誤差較大，所以一般僅考慮一步轉移矩陣，狀態轉移矩陣p（k）如下所示。

式中：p（k）表示轉移k 步的狀態轉移矩陣；pij（k）表示經k 步由狀態i 轉移到狀態j 的概率，計算公式如式（12）所示。Mi為狀態Ei出現的次數；Mij（k）為狀態Ei轉移到Ej的樣本數。

（3）基于馬爾科夫狀態轉移矩陣對人材機費用預測值進行修正，計算如式（13）所示。

3 實證分析

3.1 預測分析

選取W 市的預制構件市場作為實際案例進行分析，由于W 市預制構件市場信息價均于每月末發布當月信息指導價，難以對當月的市場經濟活動提供有效指導，存在嚴重的時滯性問題。

本文實例利用2022 年1—11 月份的預制構件市場信息價和各項經濟指標數據，數據的主要來源為實地調研的10 家大型預制構件生產企業和建設工程標準定額管理站官方網站發布的建設工程價格信息文件。出于對預制構件造價管理精細化的要求，對預制構件應分構件類型進行市場信息價的管理工作。于是，選用最常用的預制外墻板進行市場信息價的及時動態測算演示，其他類型的預制構件可參照進行。

數據采集工作分為3 個部分：

第一部分為隨時間周期變化波動明顯的人材機費用數據。經整理匯總得到2022 年1 月至2022 年11 月預制外墻板人材機費用（見表1）。

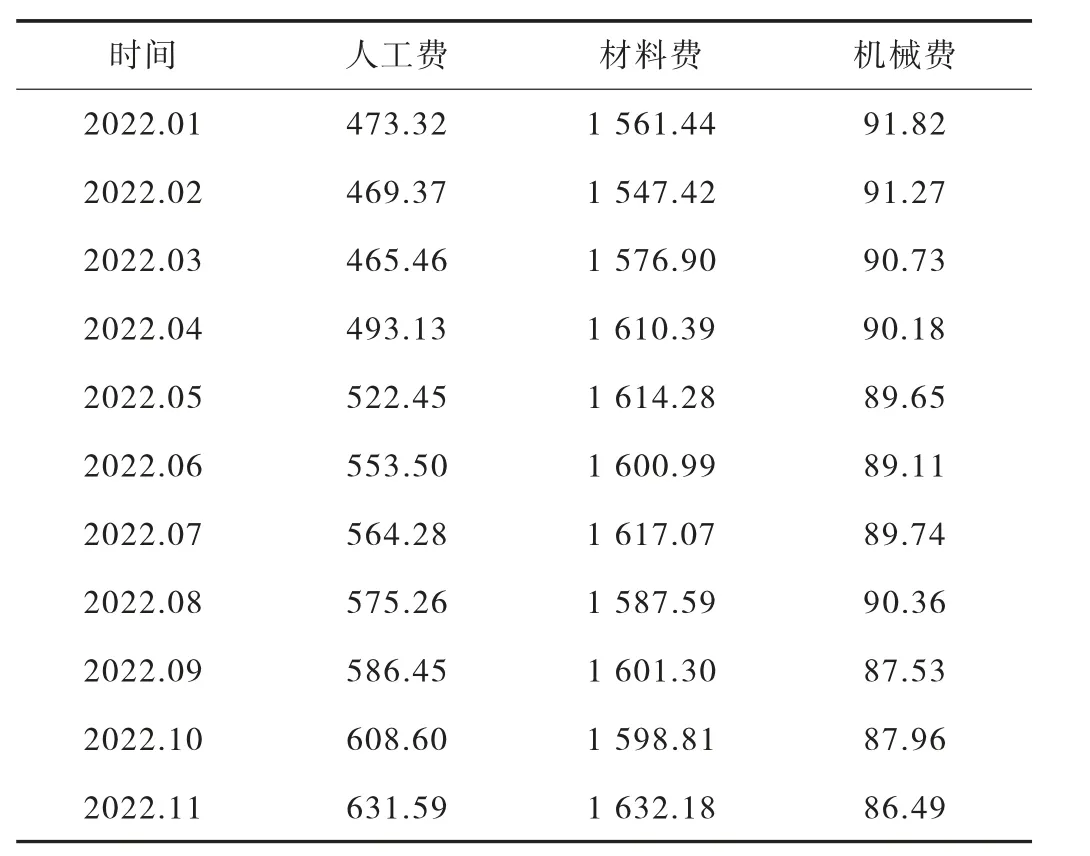
表1 預制外墻板人材機費用匯總單位：元/m3

第二部分為隨時間周期波動較小，但從較長周期來看會發生變化的折舊及攤銷、深化設計費、運輸費。經過對W 市裝配式預制構件市場調研可知，預制構件綜合單價中的折舊及攤銷、深化設計費、運輸費在以月為時間跨度的周期內保持不變，但長期會隨著達產率、標準化程度等而發生變化。

經合理測算，2022 年W 市的預制構件折舊及攤銷費平均水平為292.40 元/m3，深化設計費平均水平為98.04 元/m3，30 km 以內運費平均水平為132.74 元/m3。

第三部分為在較長周期內無變化的管理費、利潤及稅金，與現行預制構件市場費率保持一致即可。

將表1 中的數據按人材機分類分別代入到原始時間序列X0中，借助MATLAB2014a 進行計算，得到人工費的模型擬合系數a1=0.0307，b1=15040.3654。于是，人工費的SCGM（1，1）c 預測模型如式（14）所示。

同理，得到材料費的模型擬合系數a2=0.0042，b2= 37361.2332，材料費的SCGM（1，1）c 預測模型如式（15）所示。

于是，機械費的模型擬合系數a3=-0.0054，b3=-1718.0140，機械費的SCGM（1，1）c 預測模型如式（16）所示。

最后，利用式（17）表示SCGM（1，1）c 預測模型的擬合效果。

式中：δk表示第k 個月的擬合誤差。

結合式（14）、式（15）、式（16）可計算得到2022年1 月～11 月份的人材機擬合值，利用式（17）得到人工費的平均相對誤差為1.6556%，材料費的平均相對誤差為0.9152%，機械費的平均相對誤差為0.6448%，擬合效果如圖2 所示。同時，得到2022 年12 月份的人工費Lc（12）、材料費Mc（12）、機械費Mf（12）預測值，其擬合精度及擬合誤差詳見表2。

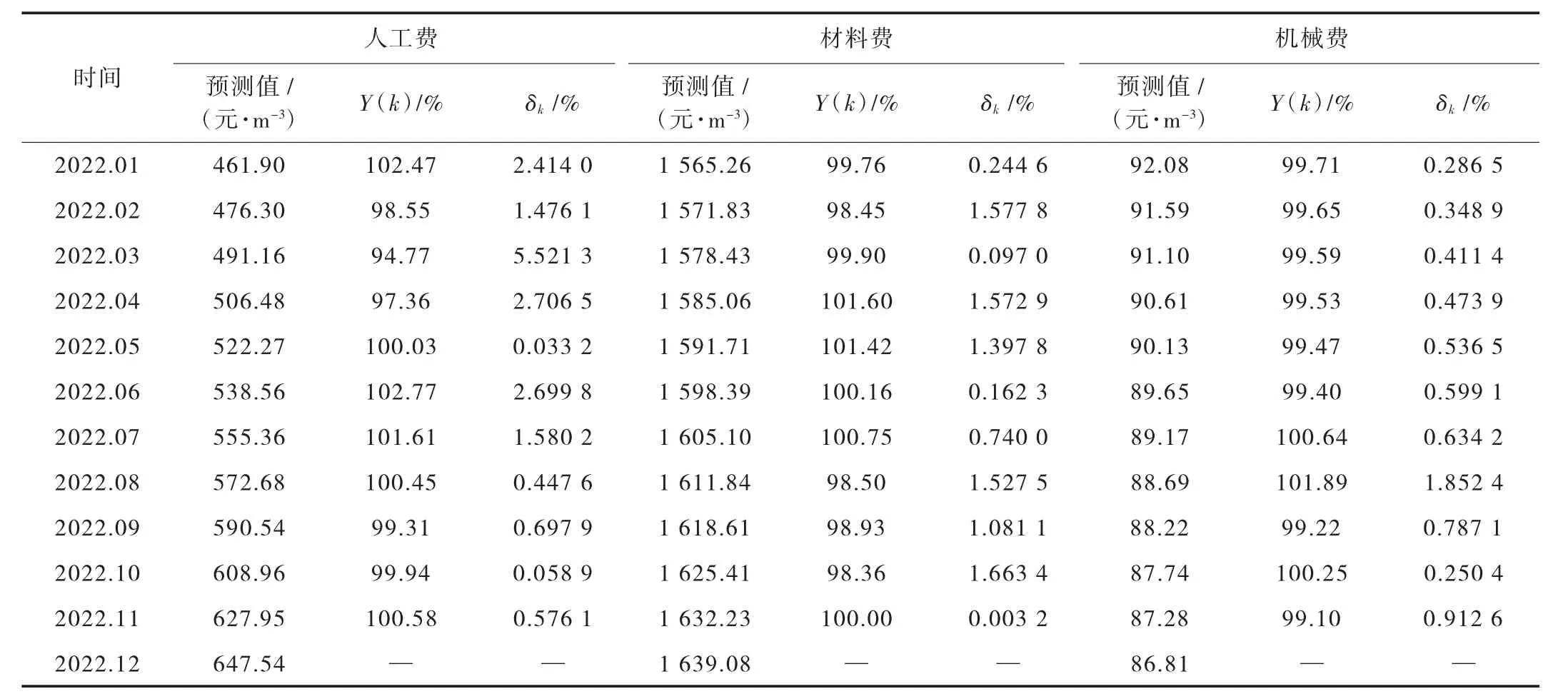
表2 預制外墻板人材機預測結果

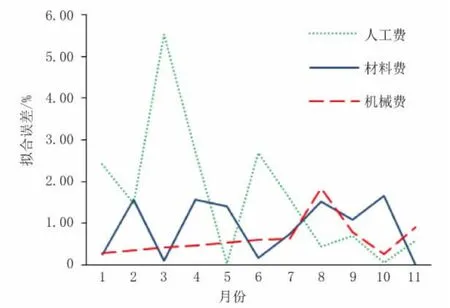
圖2 2022 年1—11 月人材機費用擬合誤差圖

由圖2 可知，人工費的擬合誤差波動幅度較之于材料費、機械費處于較大水平，材料費次之，機械費的誤差波動最小。

由于人工費、材料費、機械費的絕對值相差較大，且各自的數據變化規律、影響因素均存在較大區別，因此在利用馬爾可夫優化SCGM（1，1）c 預測模型時，應采用不同的狀態劃分。

根據表2 中的擬合精度Y（k）的結果，采用最優K 分法[12]將狀態劃分為為4 個狀態[E1，E2，E3，E4]，劃分區間詳見表3。

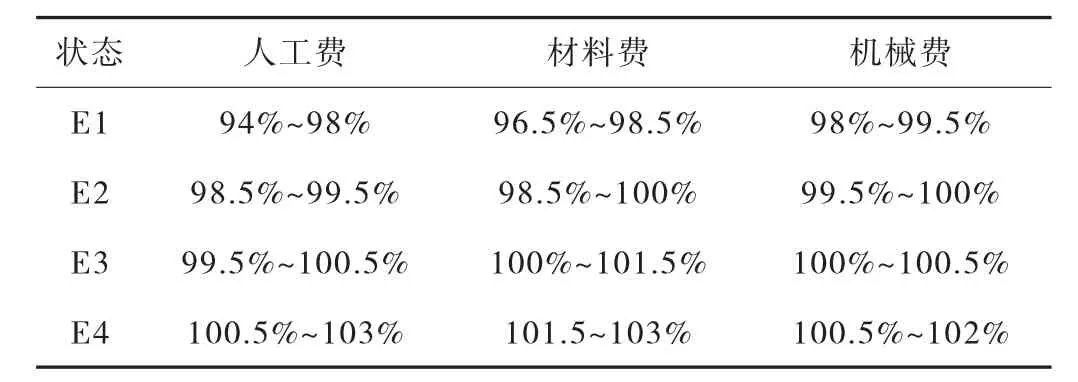
表3 狀態劃分

結合表2 中的擬合精度和表3 中的狀態劃分，繪制人工費的狀態轉移具體情形如圖3 所示。

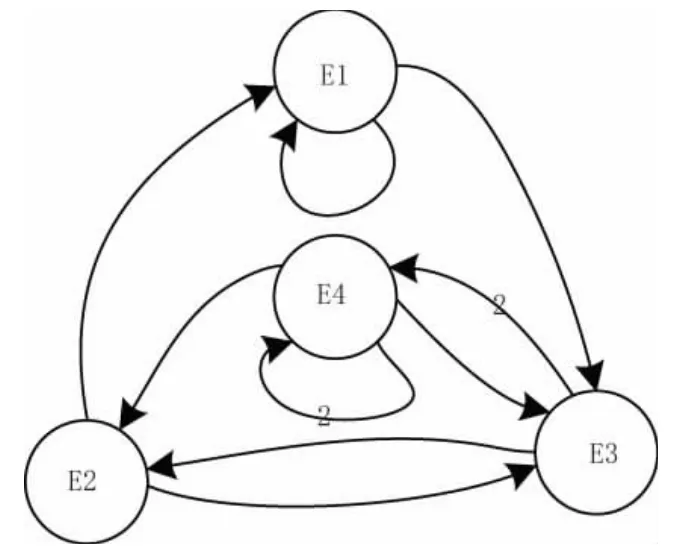
圖3 人工費狀態轉移圖

結合圖3 中各狀態的轉移情形，再根據式（12）可以計算出人工費的狀態轉移矩陣P1（1），具體如下：

由表2 知，2022 年11 月份人工費的擬合精度為100.58%，處于E4 狀態。根據其狀態轉移矩陣P1（1）可知，12 月份的人工費狀態最有可能向E4 轉移。所以，根據式（13）得到經馬爾科夫優化后的人工費預測值為：

同理，可繪制出材料費的狀態轉移圖，進而得到材料費的一步狀態轉移矩陣為P2（1）。

由表2 知，2022 年11 月份材料費的擬合精度為100.00%，處于E2 狀態。根據狀態轉移矩陣P2（1）可知，12 月份的材料費狀態最有可能轉向E1 狀態，于是經馬爾科夫優化后的材料費預測值為1598.10元/m3。

同理，機械費的一步狀態轉移矩陣為P3（1），具體如下：

2022 年11 月份的擬合精度處于E1 狀態，故12月份最有可能轉向E1 狀態，于是12 月份的機械費預測值為85.71 元/m3。

于是，根據2022 年12 月份的人材機的預測值、折舊及攤銷、深化設計費、運輸費的測定值，測算2022 年12 月的預制外墻板市場信息價為3834.05元/m3。

基于等維選取數據的思路，選取2022 年2—12月份的人材機數據作為原始時間序列代入到馬爾科夫優化后的SCGM（1，1）c 預測模型中，得到2023 年1 月份市場信息價為3876.03 元/m3。依次進行，得到2023 年2—4 月份的信息價預測值，預測結果分析詳見表4。

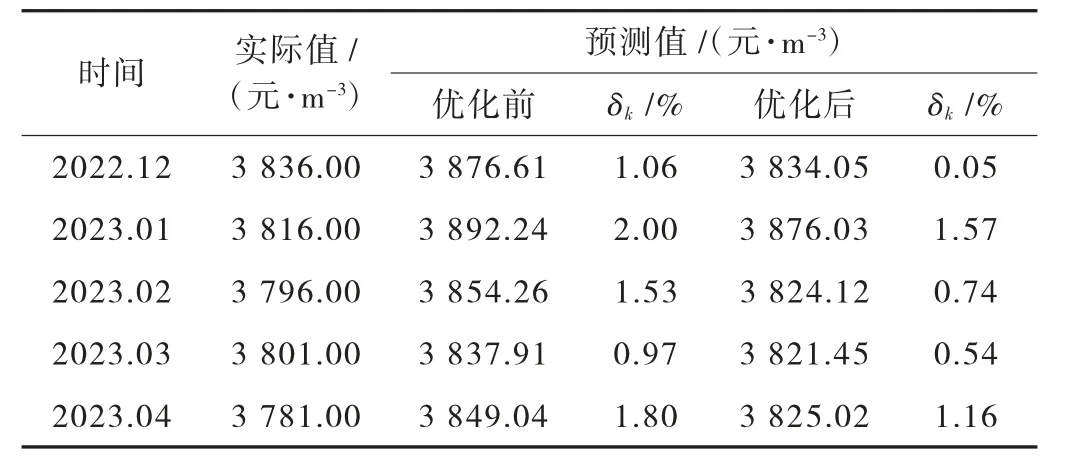
表4 預制外墻板市場信息價預測

由表4 可知，SCGM（1，1）c 預測模型的平均誤差為1.47%；經馬爾可夫優化后，預測值的平均誤差下降至0.81%，表明該模型能夠有效地為預制構件市場信息價提供預測支持。

3.2 預測模型驗證

運用W 市2022—2023 年間預制外墻板的市場信息價數據，并選取多元線性回歸模型、BP 神經網絡模型和SVM 模型進行對比，以體現本文模型的優越性。

其中，多元線性回歸模型結構、操作步驟較為簡單，主要是利用人材機數據進行多元函數的擬合，在擬合優度達到預期后即可輸出預測結果；BP 神經網絡模型和SVM 模型內部結構較為復雜，借鑒陳偉[13]在鋼材價格預測中使用的滾動預測方法，將模型輸入、輸出項設置為表5 中數據，并對模型初始化參數進行優化調整，使得預測模型的輸出值與實際值誤差更小，滿足精度要求。

表5 BP 神經網絡和S VM 模型輸入、輸出項

根據表5 中的數據選取規則，可形成模型訓練所需的數據集，然后進行模型的訓練及測試。待模型訓練完成且精度符合要求之后，輸入2022 年10 月份、11 月份的預制外墻板的人材機費用數據x0（10）、x0（11），即可輸出12 月份的預測值x0（12）。再將其代入到市場信息價動態測算模型中，得到預制外墻板12 月份的市場信息價預測值。以此類推，即可實現后續預測工作。

于是，根據以上預測思路得到4 種模型的運行對比結果（見表6）。

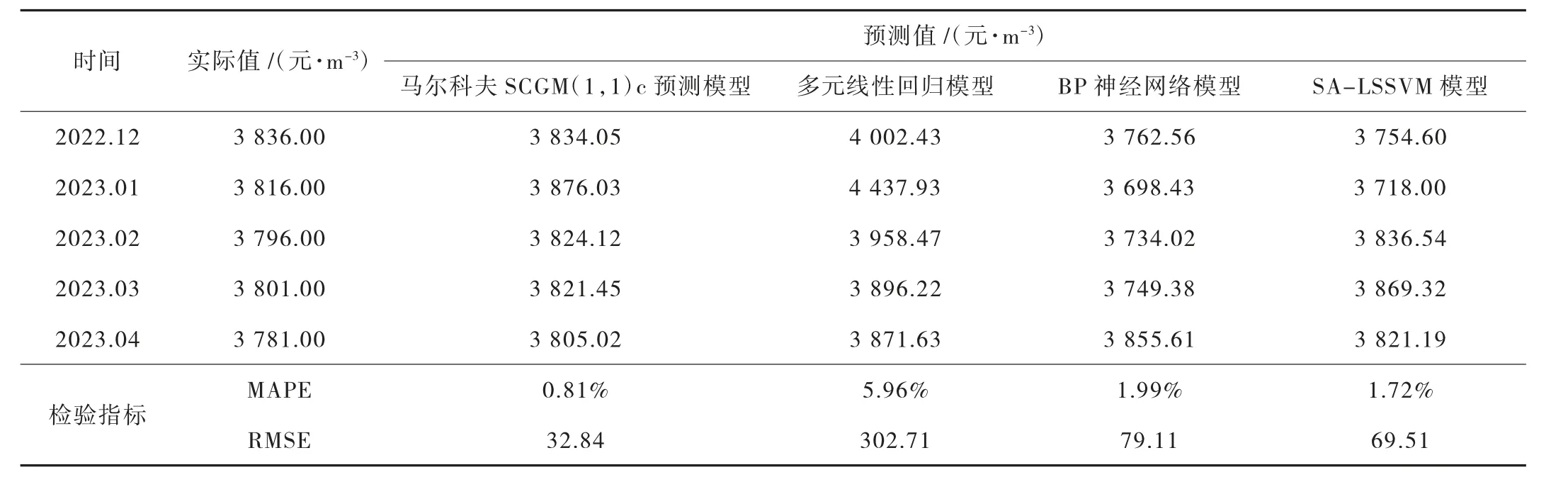
表6 預制外墻板市場信息價預測模型對比

表6 中，MAPE 為平均絕對百分比誤差，值越小,表明整體預測效果越好，計算公式如式（18）所示；RMSE 為均方根誤差，值越小，表明預測樣本數據個體之間擬合性能越好，計算公式如式（19）所示。

由表6 各數據指標可知，針對樣本個數較少的時間序列數據，馬爾科夫優化后的SCGM（1，1）c 預測模型整體表現出了很好的預測效果，可以很好地實現預制構件市場信息價的預測工作；適用于小樣本數據預測的優化后的SVM 模型也表現出了較好的預測性能，但RMSE 值過大，表明預測穩定性差；依賴于大數據的神經網絡的MAPE 值與SVM 模型較為接近，但穩定性依然較差；多元線性回歸模型擬合效果最差，且預測數據與實際數據之間的離散程度高，不適宜用于小樣本數據的預測工作。

4 結語

針對我國目前預制構件市場信息價發布機制建立初期的現狀，利用馬爾科夫優化后的SCGM（1，1）c預測模型進行預制構件市場信息價的動態測算模型研究，得到如下結論：

（1）本文建立的預制構件市場信息價動態測算模型方法可有效地解決市場信息價發布滯后的現狀，可進一步規范和引導預制構件市場，實現造價管理的精細化。

（2）經實證分析表明，SCGM（1，1）c 預測模型更適用于樣本數據少、規律性不強且存在隨機波動的預測工作，經馬爾科夫優化后具有較高的預測精度，進一步提升了SCGM（1，1）c 預測模型的適用性和穩定性。

（3）本文提供的預制構件市場信息價的預測思路，可為類似具有時間序列特征的預測工作提供參考。