三峽庫區巴東水文站蒸發模型研究

王玉濤,付 鑫,呂超楠,伍 勇

(1.長江水利委員會水文局 長江三峽水文水資源勘測局,湖北 宜昌 443000; 2中國長江三峽集團有限公司,湖北 宜昌 443000)

0 引 言

水面蒸發是自然界水循環中最基本的因素之一,也是水庫、湖泊等自然水體水量損失的主要原因。中國新疆北部平原區大型水庫年蒸發損失可占水庫總蓄水量的40%[1]。因此,水面蒸發的科學估算一直是水文學和氣候學研究的重點之一[2]。

水面蒸發過程受各種條件(如氣象、土壤、植被等)的影響,在自然條件下獲得蒸發量的絕對數值較為不易。因此,基于氣象要素的水體蒸發估算方法在實際應用中較廣泛,利用氣象要素計算蒸發的模型研究較多,目前常用的水面蒸發模型主要有彭曼模型、質量轉移模型和道爾頓模型[3-5]。彭曼模型需要使用水面輻射平衡資料,而中國觀測太陽輻射的站點很少,觀測水面輻射平衡的站點更少,使彭曼模型的應用受到很大限制。質量轉移模型的結構簡單,在歐美許多國家普遍使用,但在中國的使用效果較差,主要原因在于該模型中E/Δe-W(E為蒸發量,Δe為飽和水汽壓差,W為風速) 關系的模擬采用了最簡單的正比例函數,不符合中國氣候特點。道爾頓模型的結構也較簡單,在中國各地應用廣泛,但由于水面蒸發對微地形、微氣象條件的影響非常敏感,加上近地面空氣水平平流對蒸發器測蒸發量及其與氣象因素關系的影響突出,造成水面蒸發經驗公式具有很強的局地性特征。因此正確認識水面蒸發量與氣象因子之間的關系,建立區域性的水面蒸發計算公式,對于水庫水面蒸發的模型研究具有重要作用[6-7]。

本文分析三峽庫區巴東水文站水面蒸發及氣象數據,基于灰色關聯度和偏相關系數分析蒸發與氣象因子(氣溫、水汽壓、蒸發池內水溫、風速、日照等)的相關度,采用5種不同的蒸發模型(通用公式、李萬義修正模型、回歸模型、BP和ELM 神經網絡)定量解析不同氣象要素對蒸發趨勢的貢獻,分析了不同蒸發模型在率定期和檢驗期擬合精度及相關性。

1 研究區域概況

三峽水庫位于四川盆地與長江中下游平原交界處,控制長江上游流域面積約100萬km2,占長江流域總面積的55.6%。三峽水庫蓄水后形成的庫區長達663余km,屬河道型水庫,平均寬度1.63 km,水面面積達1 000余km2,總庫容393億m3。三峽水庫除了具有防洪、發電和航運作用外,也是重要水源地,三峽庫區人口稠密,工農業、生活用水直接關系到國計民生。水面蒸發水量損失占水庫、湖泊等自然水體水量損失的比例大,為研究三峽庫區水面蒸發變化規律和估算庫區水面蒸發損失量,2013年8月1日設立巴東漂浮水面蒸發實驗站(以下簡稱“巴東站”,110°22′E,31°03′N),2017年國家批準為水文站。巴東站位于長江三峽庫區湖北省恩施州巴東縣信陵鎮沿江路38號右岸,距三峽大壩71 km,設有陸上蒸發觀測場和漂浮蒸發觀測場,陸上觀測場場地高程183 m(吳淞資用),觀測項目有降水量、蒸發量、氣溫、相對濕度、大氣壓、水汽壓、風速風向、水溫(蒸發池內)、日照,多年來為研究三峽庫區水面蒸發量及其變化規律收集大量基本資料。本文根據巴東站2013年8月至2022年7月實測數據對蒸發模型進行分析,研究選取2013年8月至2020年7月共84個月資料作為模型率定期,以2020年8月至2022年7月共24個月作為模型檢驗期,采用SCE-UA[8]自動優化算法,以確定性系數最高和蒸發總量相對誤差絕對值最小為目標,通過Matlab自編程序進行模型參數的優化率定。

2 研究方法

氣溫、風速、相對濕度等氣象因子對水面蒸發都有很大的影響,在進行模型構建之前,需要通過相關性分析正確認識水面蒸發量與氣象因子之間的關系,以獲取相關性強的影響因子進行水面蒸發模型研究,進一步提高模型模擬精度。巴東站陸上觀測收集的氣象因子見表1。考慮資料的年系列情況,經分析計算后,采用以月尺度進行模型構建;首先基于日序列統計資料得到月序列資料,再分別采用灰色關聯度、偏相關系數分析研究陸上月蒸發量與各氣象因子的相關度。巴東站陸上水面蒸發與氣象因子相關性計算結果如表2所示。

表1 巴東站蒸發氣象因子Tab.1 Meteorological factors of evaporation at Badong Hydrological Station

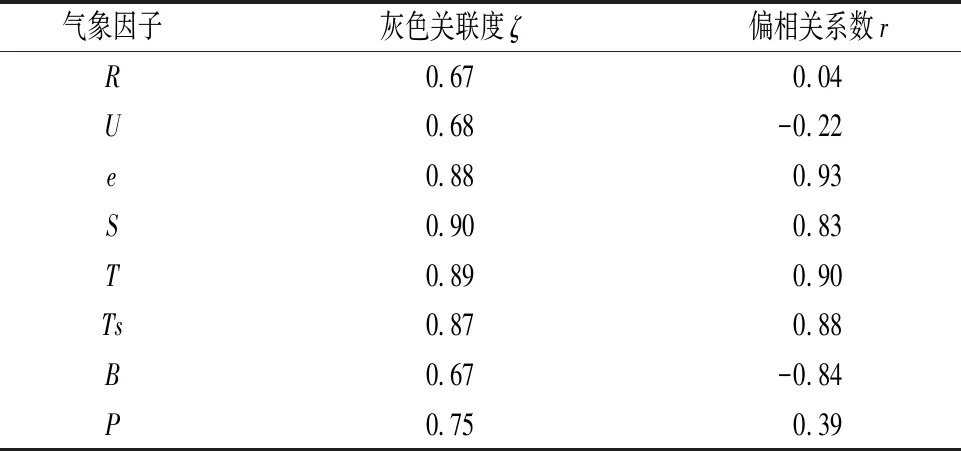
表2 蒸發與氣象因子相關性統計Tab.2 Correlation between land surface evaporation and meteorological factors

由表2可知,灰色關聯度ζ、偏相關系數r的值有一定差異,但是灰色關聯度與偏相關系數所體現的相關程度較一致,相關指數大于0.8的有:月平均水氣溫水汽壓差、月日照小時數、月平均氣溫及蒸發池內月平均水溫,說明這幾項對蒸發的影響較大。

水面蒸發是一個非常復雜的過程,影響因素多。水面蒸發量模型的研究已有200多年的歷史。自19世紀80年代以來得到許多研究成果,但絕大多數蒸發模型是利用局部地區單站觀測資料,由經驗公式分析取得的純經驗模型或半經驗模型。本文結合巴東站測站特性、地理位置、氣象因子相關性、資料序列等,采用灰色關聯度、偏相關系數以及適用性綜合分析后,選用經驗公式、修正模型以及數學模型等方法,對巴東站陸上蒸發模型進行分析。

3 模型構建及計算結果分析

3.1 通用公式及其計算結果

由濮培民等提出的通用公式,分析了水面蒸發過程中水-氣界面上質量、能量和動量傳遞過程以及水文、氣象要素對水面蒸發的線性影響[9],用鮑文比和層結穩定度兩個無量綱量,結合蒸發有效風速,建立水面蒸發量的計算模型。根據本站收集到的蒸發、氣象資料,不僅包括氣溫還有蒸發池水溫、水汽壓、風速等數據,滿足通用公式的計算,計算公式如下:

(es-ea)

(1)

式中:μ為水面以上風速,m/s;ΔT為水汽溫差,℃;es為水面水汽壓,hPa;ea為水面以上1.5 m處空氣中的水汽壓,hPa;當ΔT≥0時,c=0,當ΔT<0時,c=0.01;此模型不包含氣壓、相對濕度因子。

由通用公式精度評定(表3)和通用公式模擬與實測月水面蒸發量變化過程(圖1)可以看出,通用公式模型率定期的確定性系數為0.939 3,蒸發總量相對誤差為0.13%,模型模擬的蒸發過程與實測過程較一致,效果較好;檢驗期的確定性系數較小,效果較差。總體而言,蒸發量計算值與觀測值的相關性較好,總體模擬結果比較理想,后續還需加強分析。

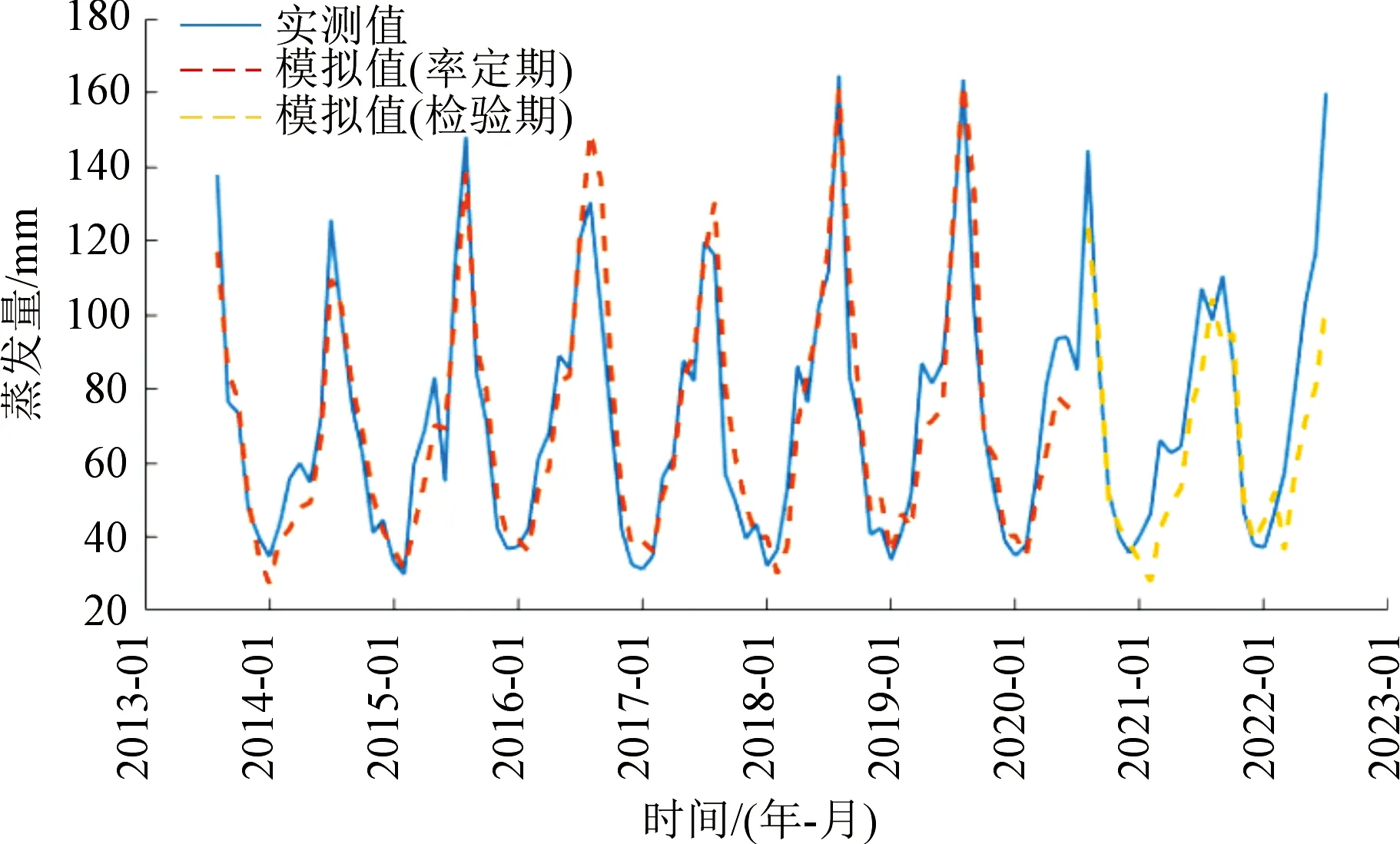
圖1 通用公式模擬與實測月水面蒸發量變化過程Fig.1 Simulation and measurement of monthly water surface evaporation by general formula

表3 通用公式精度評定Tab.3 Accuracy evaluation of general formula

3.2 李萬義修正模型及其計算結果

李萬義公式對水面蒸發物理過程作了部分假設,適用于全國范圍的水面蒸發量計算模型,此模型結構比較簡單[10]。水面蒸發是在一定的熱力學條件與動力學條件的共同作用下產生的,英國學者彭曼根據水面蒸發的形成機制,通過聯解空氣動力學方程和能量平衡方程,得出計算水面蒸發的組合型公式,該公式是依據英國特定的海洋性氣候條件下取得的實驗資料建立的,而中國絕大多數地區處在典型的季風氣候區,因此原型彭曼公式不宜在中國應用[11]。結合本站收集的數據,依據李萬義公式的框架和彭曼公式[12],進行模型構建,擬建立李萬義修正公式(LWY)如下:

(2)

式中:a,b,c,d,f為待定參數;ez為飽和水汽壓,hPa,由蒸發器內水溫和氣溫綜合求得;R為平均相對濕度,以小數計;el為實測平均水汽壓,hPa;T為氣溫,℃;此模型未包含氣壓因子。

模型涉及的參數有5個。本研究選取2013年8月至2020年7月共84個月資料作為模型率定期,以2020年8月至2022年7月共24個月作為模型檢驗期,采用SCE-UA[8]自動優化算法,以確定性系數最高和蒸發總量相對誤差絕對值最小為目標,通過Matlab自編程序進行模型參數的優化率定。經過模型率定后,得出LWY水面蒸發模型參數及精度評定結果見表4和圖2。

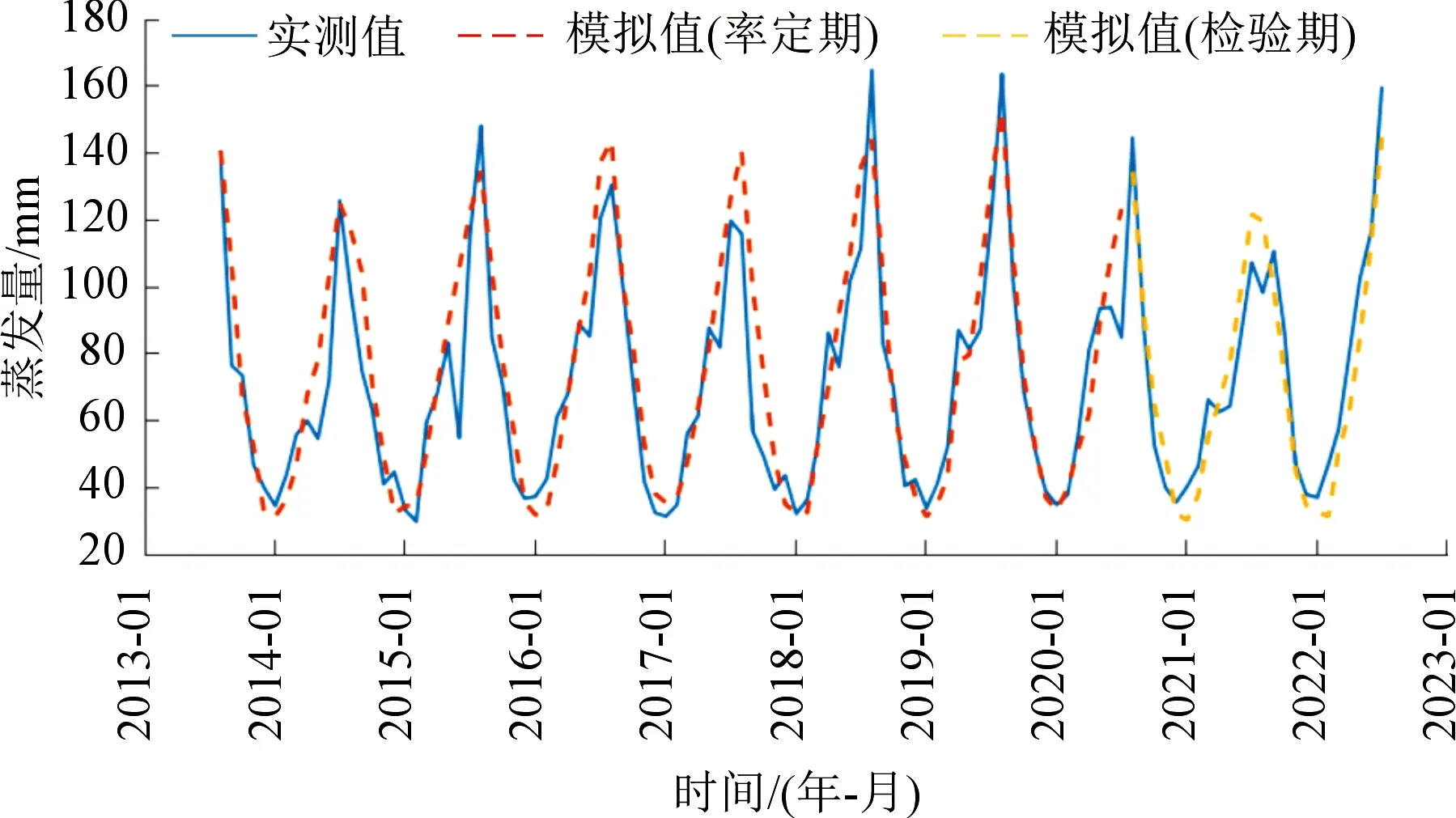
圖2 LWY模擬與實測月水面蒸發量變化過程Fig.2 LWY simulation and measured monthly water surface evaporation process

表4 LWY水面蒸發模型參數及精度評定Tab.4 Parameters and accuracy evaluation of LWY water surface evaporation model

由表4和圖2可以看出,無論是檢驗期還是率定期,LWY模型的確定性系數均超過0.90,蒸發總量相對誤差均在±7%以內。模型模擬的蒸發過程與實測過程較一致,檢驗期的蒸發相關散點在率定期范圍內,蒸發量計算值與觀測值的相關性較好,總體模擬結果比較理想,表明LWY水面蒸發模型構建準確,精度較高。

3.3 回歸模型分析及其計算結果

由于氣象因子與水面蒸發存在較為顯著的線性相關性,故從多元線性回歸[13]角度考慮構建水面蒸發線性回歸模型,采用偏最小二乘法(PLS)回歸模型進行參數率定,得到如下回歸模型:

E=a1+a2R+a3U+a4e+a5S+

a6T+a7B+a8TS+a9P

(3)

式中:a1～a9為模型待定參數。

模型涉及的參數有9個。表5給出了PLS水面蒸發模型參數及精度評定結果。圖3為回歸模型與實測月水面蒸發量變化過程。

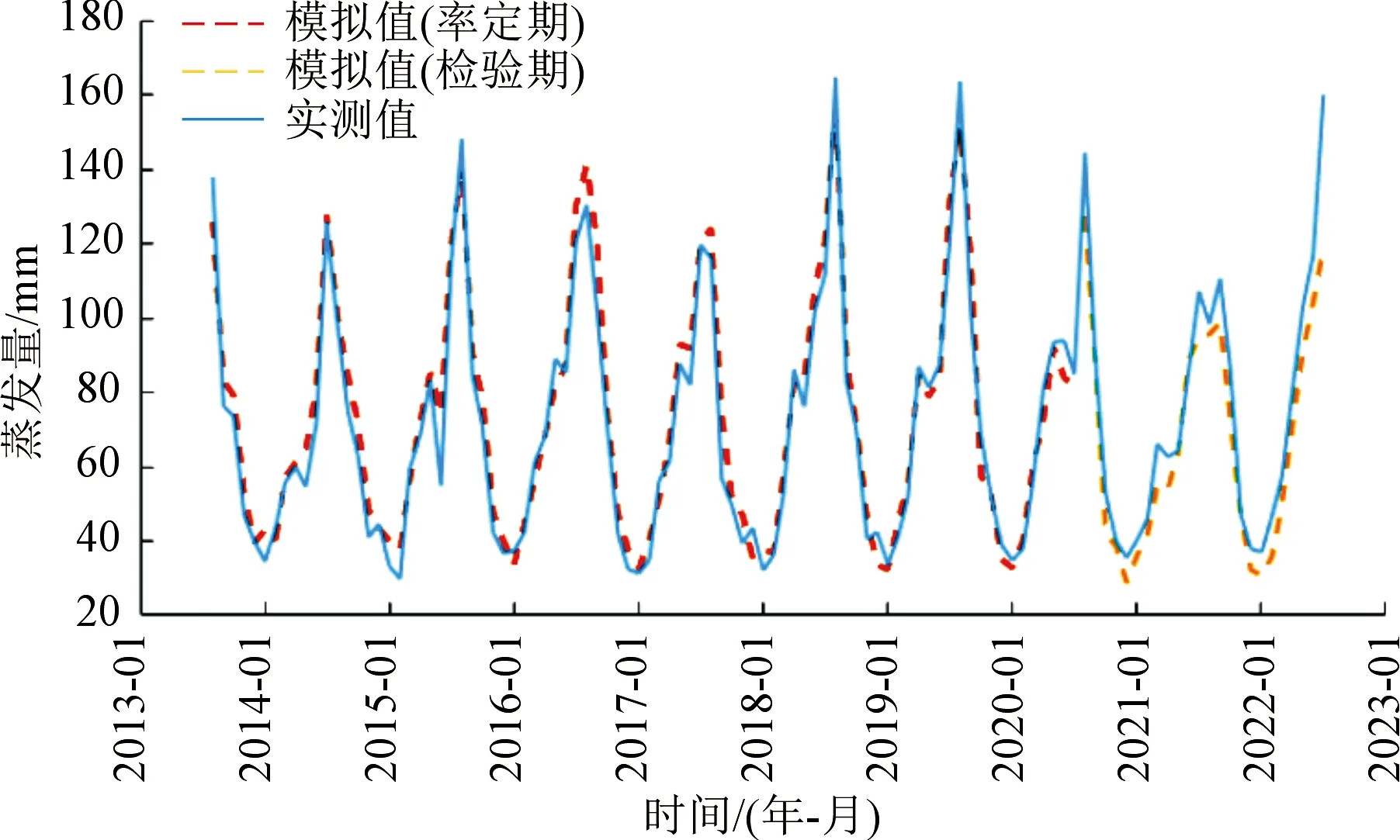
圖3 回歸模型與實測月水面蒸發量變化過程Fig.3 Regression model and measured monthly water surface evaporation process

表5 回歸模型參數及精度評定Tab.5 Regression model parameters and accuracy evaluation

由圖3和表5可以看出,采用回歸模型進行月蒸發的模擬同樣表現出較高的精度。無論是檢驗期還是率定期,模型確定性系數超過0.90,蒸發總量相對誤差在率定期較小,檢驗期偏大,參數率定有較好的效果,能夠較好地擬合水面蒸發變化過程。

3.4 復雜數學模型及其計算結果

隨著計算機技術的不斷提高,一些復雜數學蒸發模型[14-15]也被運用到相關指標的模擬。最為常見的有人工神經網絡(BP、ELM)[16]。本文嘗試采用BP和ELM人工神經網絡進行水面蒸發模擬。經過模型率定后,得出人工神經網絡(BP、ELM)水面蒸發模型參數及精度評定結果,見表6和圖4～5。

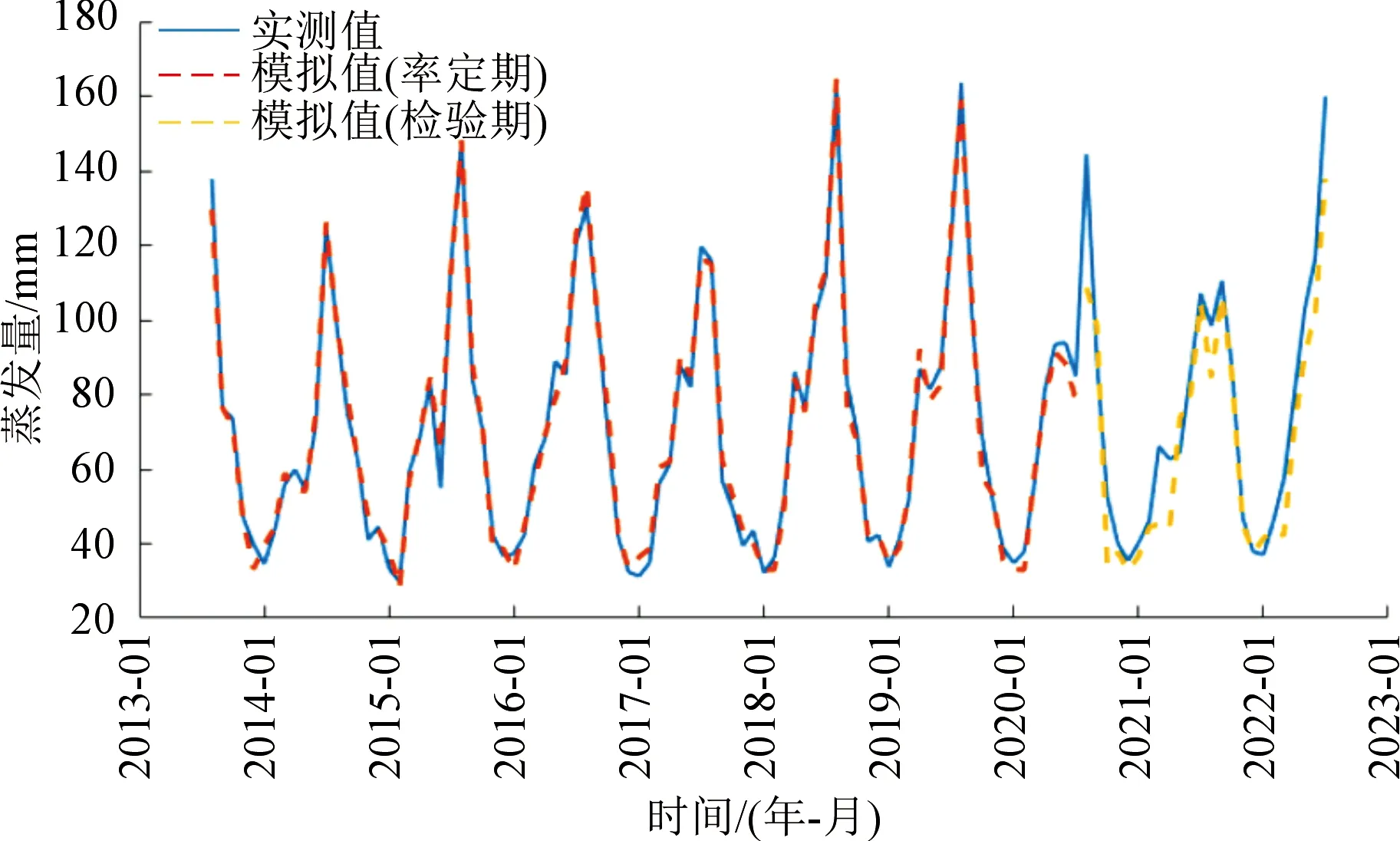
圖4 ELM神經網絡模型與實測月水面蒸發量變化過程Fig.4 ELM neural network model and measured monthly water surface evaporation process

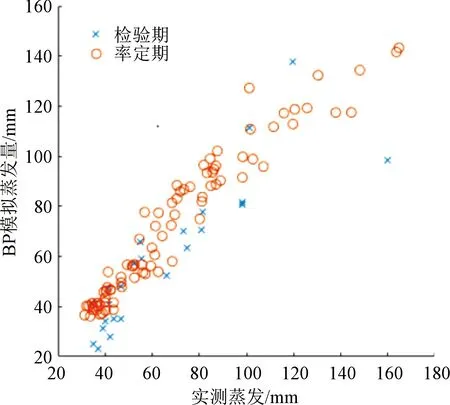
圖5 BP神經網絡模型與實測月水面蒸發量散點圖Fig.5 BP neural network model and scatter chart of measured monthly water surface evaporation

表6 神經網絡模型參數及精度評定Tab.6 Neural network model parameters and accuracy evaluation

由圖4～5和表6可以看出,采用人工神經網絡(BP、ELM)進行月蒸發的模擬同樣表現出較高的精度,率定期模型確定性系數均超過0.90,但BP模型在檢驗期表現相對較差;蒸發總量相對誤差在率定期較小,檢驗期偏大。

4 水面蒸發模型分析

本次研究共采用5種方法構建水面蒸發模型,分別是回歸模型(PLS)、李萬義修正模型(LWY)、通用公式、BP神經網絡、ELM神經網絡。各模型的模擬精度存在差異,為更好地對模型的適用性進行比較分析,各種月模型在檢驗期、率定期的指標(確定性系數和總量相對誤差)見圖6～7。

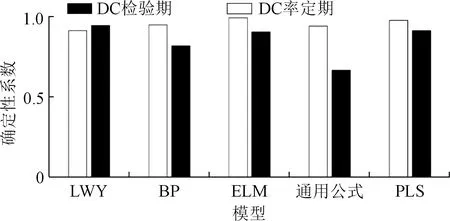
圖6 各模型確定性系數Fig.6 Deterministic coefficients of each model

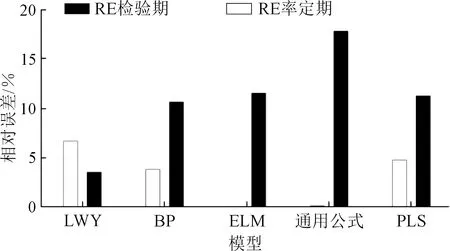
圖7 各模型蒸發總量相對誤差Fig.7 Relative errors of total evaporation of each model

由圖6～7可知,5種模型構建準確,各模型模擬精度均較高,率定期各模型確定性系數均高于0.90,總量誤差控制在±10%之間,均適用于陸上月尺度蒸發量的模擬;在率定期,相比PLS、LWY、通用公式、BP神經網絡這4種模型,ELM神經網絡模擬精確相對較高,確定性系數最高0.992 3,且蒸發總量相對誤差的絕對值也最小,模型適用性最強;在檢驗期,則是LWY相對效果較好。綜合分析,LWY更優,更能適用巴東站陸上水面蒸發計算。

5 結 論

本文結合巴東站氣象數據,對三峽庫區巴東站陸上蒸發模型進行研究,選取2013年8月至2020年7月共84個月資料作為模型率定期,以2020年8月至2022年7月共24個月作為模型檢驗期。分別采用回歸模型(PLS)、李萬義修正模型(LWY)、通用公式、BP神經網絡、ELM神經網絡,共5種方法構建水面蒸發模型,5種模型構建準確,各模型模擬精度均較高,率定期各模型確定性系數均高于0.90,總量誤差控制在±10%之間,均適用于陸上月尺度蒸發量的模擬。各模型的模擬精度存在差異,率定期ELM神經網絡模擬精確相對較高,各統計指標更合理,但檢驗期LWY相對效果更好,各統計指標更合理。總體來說,LWY更適合作為巴東站陸上蒸發模型使用,PLS、通用公式、BP神經網絡、ELM神經網絡構建水面蒸發模型均可作為參考使用。