淺談整體觀下圖形變化的層級探究

崔麗楠

摘要：初中階段，圖形的變化主要為折疊（軸對稱）、旋轉、平移這三類基本的圖形運動。“圖形的變化”強調從運動變化的觀點來研究圖形，理解圖形在軸對稱、旋轉和平移時的變化規律和變化中的不變量。圖形折疊的相關知識、解題方法等在不同年級和章節比較零散，不夠系統全面。大單元教學的核心目標就是將零散的知識進行整合，將知識進行關聯。[1]

關鍵詞：整體結構 圖形的變化 折疊

在目前的學校教學中，發展學生的核心素養已成為必然趨勢。 核心素養具有整體性、一致性和階段性，在不同階段具有不同表現。《新版課程標準解析與教學指導（2022年版）》更加強調了知識的整體性和連貫性，到了初中階段，學生對圖形的理解上升到對圖形性質、關系、變化規律的理解，因此要培養學生初步的抽象能力、理性思維、幾何直觀和空間想象力，能在實際情境中，識別出生活中的軸對稱、平移和旋轉的現象，并能直觀感受平移、旋轉和軸對稱的特征。[2]圖形的折疊（軸對稱）是幾何圖形三種圖形變換中的一種。北師大版教材呈現的知識結構與各時段的課標要求不同。而九年級時，圖形折疊問題綜合性比較強，解題思路比較廣，解題方法靈活。所以，對圖形的變化在不同學段進行不同的滲透是非常有意義的。在學習了角平分線和平行線之后，筆者以折疊中探究平行線性質與判定為例，淺談大單元教學引導下，在七年級如何滲透圖形的變化。

一、教學過程

（一）一次操作，初步感知

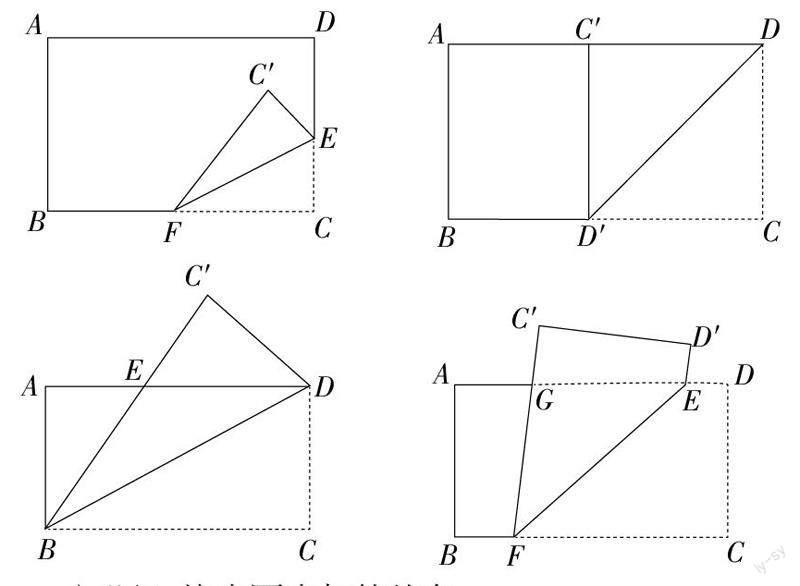
學生動手操作，折疊一張矩形紙片。 觀察折疊后相等的角。展示學生的折疊作品如下：

問題1：找出圖中相等的角。

問題2：圖2中，∠AC′D′的度數是多少？

問題3：圖3中，三角形EBD的形狀？

問題4：圖4中，圖中有幾組平行線？若∠EFC=40°，則∠GED′的度數？

功能分析：折紙活動對于七年級的學生來說是件有意義的事情，能激發學生的學習積極性。在操作過程中，通過大家不同的折紙方式，首先可以通過操作感受數學中的分類思想。其次，通過觀察，直觀感受折疊的軸對稱作用，從而找到相等的角，利用問題串，將探究的問題一步步加深。問題1通過找相等的角感受折痕的角平分線的作用。問題2感受折疊前后的全等，邊相等、角相等。問題3將角平分線與平行線結合，利用平行線的性質，得到∠EBD=∠EDB。

問題4發現存在兩組平行線，兩組平行線的結合，兩組角平分線的結合進行求解。本次操作活動，既發展了學生的動手操作能力，又提升了學生的歸納總結能力。

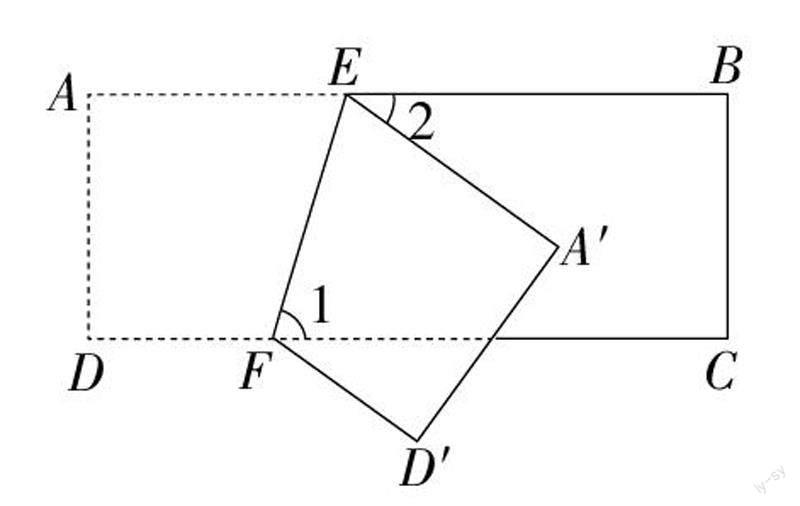
例1：如圖，四邊形ABCD為一矩形紙帶，點E、F分別在邊AB、CD上，將紙帶沿EF折疊，點A、D的對應點分別為A'、D'，若∠2=35°，則∠1的度數為（）?

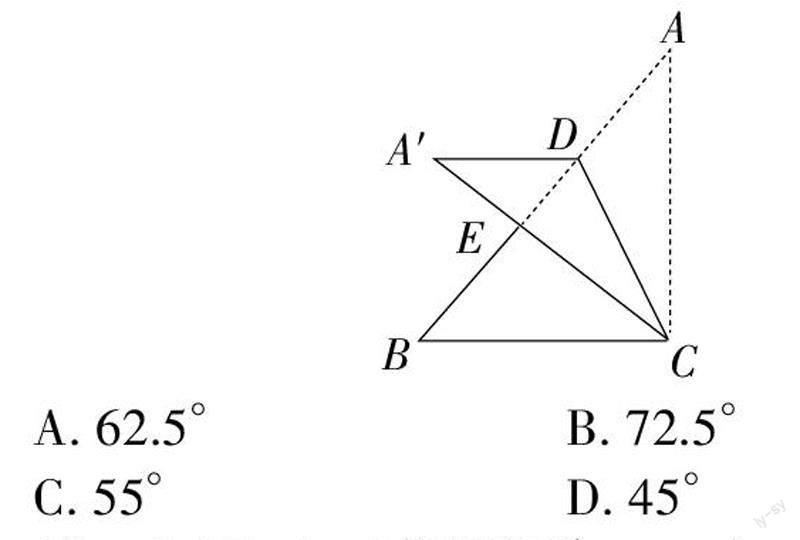
例2：如圖，在三角形紙片ABC中，∠ACB=90°，∠A=40°，點D在AB邊上（不與A、B重合），連接CD，將△ACD沿CD所在直線折疊得到△A′CD，A′C交AB于點E.如圖，若A′D∥BC，則∠ACD的度數為? ? ?；

設計意圖：小試牛刀，例1將折疊與矩形結合，既加深折痕是角平分線的作用，又結合平行線的性質來求解。例2通過折疊三角形，鞏固折疊前后對應角相等，折痕是角平分線的作用。對學生通過操作觀察得到的結論轉化為實踐探究，發展理性思維能力。

（二）二次操作，總結歸納

例3：如圖，長方形紙片ABCD，點E，F分別在邊AB，CD 上，連接EF，將∠BEF對折，點B落在直線EF上的B′處，得折痕EM；將∠AEF對折，點A落在直線EF上的點A′處，得折痕EN，則∠MEN的度數為_________。

功能分析：在活動一中圖1的基礎之上繼續進行操作，通過二次折疊，繼續感知折痕是角平分線的作用。 通過實際操作，學生可觀察出七年級上冊學習角平分線時涉及到的雙角平分線模型，此過程學生由實踐操作再次進行提煉、歸納總結。

例4：如圖，長方形紙片ABCD，將∠ADC和∠ABC分別沿著DD′、BB′對折，使得點A落在邊CD上，點C落在邊AB上，請問兩條折痕DD′、BB′的位置關系如何？為什么？

功能分析：在活動一的圖2基礎之上繼續進行操作，結合七年級所學的平行線知識，將角平分線和平行線相結合。教師在引導學生解題的過程中，領著學生進行分析結論，分析條件。學生經歷觀察猜想，驗證推理的過程。

變式練習：（2023春·太原期中變式）綜合與實踐

問題情境：

數學課上，同學們以“長方形紙帶的折疊”為主題開展數學活動，已知長方形紙帶的邊AD∥BC，將紙片沿折痕EF折疊，點A，B分別為點A'，B'，線段B′F與DE交于點G。（說明：折疊后紙帶的邊A′E∥B′F始終成立）

操作探究：

（1）如圖1，若B′F⊥AD，則∠EFG的度數為_________°；

（2）如圖2，改變折痕EF的位置，其余條件不變，小彬發現圖中∠1=∠2始終成立，請說明理由；

（3）改變折痕EF的位置，使點 B'恰好落在線段AD上，然后繼續沿折痕MN折疊紙帶，點M，N分別在線段FC和B′D上.如圖3，點C，D的對應點分別為點C′，D′，點C′，D′均在AD上方，若∠BFE=α，∠CMN=β，當FB′∥MC′時，直接寫出α與β之間的數量關系。

例5：如圖，把長方形ABCD的兩角折疊，折痕分別為EF、HG，點B、D折疊后的對應點分別是B'、D'，并且使HD'與B'F在同一直線上，已知長方形的兩組對邊分別平行，試找出圖中相互平行的直線。

功能分析：難度升級，問題具有開放性。學生自己找出平行線段，首先需要經歷直觀觀察，猜想再進行證明。 此題綜合性較強，但還是需要抓住其本質，在折疊過程中，哪些量是不變量，比如∠EB'F=90°，∠HD'G=90°，從而得到EB'∥D'G。 另一方面，折疊過程中，抓住折痕相當于角平分線這一特征，如∠GHD'=1/2∠DHF，∠EFB'=1/2∠BFH。又∠DHF=∠BFH，從而得到EF∥GH。 本節課的探究方式對于后續圖形的變化的學習具有方法上的點撥。

變式練習：如圖所示，一張長方形紙片ABCD（∠A=∠B=∠C=90°），先將紙片沿EF折疊，再將折疊后的紙片沿GH折疊，使得GD′與A′B′重合，展開紙片后若∠BFE=62°，則∠DGH=_________°。

二、教學思考

（一）整體結構性有助于眼中有木，心中有林

圖形的運動，平移、旋轉、軸對稱對于九年級的學生來說，是至關重要的，并且難度也比較大。 將本節課內容放到整個幾何知識板塊中，只是一小部分而已。當然，在學習了三角形之后，將折疊與三角形相結合。 學習軸對稱之后，折痕還具有中垂線的作用，但是通過本節課的學習，學生在后續的探究中，就會學會從什么角度入手來進行探究。 在初一階段，將折疊的求角度問題滲透，在八年級學習了勾股定理，將折疊與求邊長相結合。 學習了平面直角坐標系，再將圖形折疊放到平面直角坐標系中進行研究。九年級學生在進行探究與思考時，對于此類型題目就會游刃有余。 但我們在本階段教學時一直在強調關鍵詞“角平分線”，并且一直在關注不變量，抓住本質所在。

（二）即時歸納提煉有助于整體知識建構

我們一直想讓學生積極參與課堂，努力做到不僅課堂高效，而且學生樂學。本節課重在學生動手操作，獨立思考，教師引導。設計體現了操作的本質和特征。重點研究操作前后對應線段、對應角的變與不變。強調由操作得到的圖形之間特殊的位置關系和數量關系。此外，教學設計不止于操作，還把操作活動上升到思維層面，把實際問題轉化為數學問題。將本質的、共同的、核心的要素進行即時性的歸納總結，培養學生進行直觀猜測、數學抽象、邏輯思維等。這種研究圖形變化的思想在七年級進行滲透，有助于遷移到今后的學習探究中。

參考文獻：

[1]張存敬.第1講操作性問題[J].中學數學教學參考，2022（3）：51-54.

[2]中華人民共和國教育部.義務教育數學課程標準（2022）版[M].北京：北京師范大學出版社，2022.